Методы расчета частотных характеристик разомкнутых сервоприводов и систем управления

Для проведения оценки соответствия выбранному критерию устойчивости, а также определения запасов устойчивости по фазе и амплитуде на этапе проектирования сервоприводов, регуляторов и следящих систем управления, к которым, в частности, относятся системы управления вектором тяги ракетных двигателей, требуется вычисление их разомкнутых амплитудно-частотных характеристик (АЧХ) (логарифмических ампли-тудно-частотых характеристик (ЛАЧХ)) и фазовых частотных характеристик (ФЧХ).

Как показано в работе [1], частотные характеристики линейных или линеаризованных моделей приводов, регуляторов и следящих систем, замкнутых отрицательной обратной связью, можно получить из их переходных характеристик, используя принцип взаимно-однозначного соответствия между функциями в области действительных переменных и комплексных переменных, осуществляемых преобразованиями Фурье и Лапласа. Такие алгоритмы и соответствующие им компьютерные программы широко известны [2–4], а один из них был реализован в программе расчета частотных характеристик рулевого привода ракеты-носителя «Энергия» [5] для его линеаризованной модели.

В то же время известно, что достоверные частотные характеристики для существенно нелинейных моделей сервоприводов и систем управления могут быть получены только посредством возбуждения таких объектов моногармоническими входными сигналами на различных фиксированных частотах с последующим анализом реакций на эти возбуждения методом Фурье [6–8].

Если нелинейность объекта несущественна, то приближенные частотные характеристики для таких замкнутых обратной связью сервоприводов и систем управления можно получать из их переходных характеристик. Однако методы расчета частотных характеристик разомкнутых сервоприводов и систем управления остаются неразвитыми. Поэтому целью настоящей работы является разработка методов расчета частотных характеристик разомкнутых сервоприводов и систем управления с использованием частотных характеристик замкнутых сервоприводов и систем управления, получаемых с использованием преобразований Фурье и Лапласа из переходных характеристик, вычисляемых по их линейным или линеаризованным математическим моделям, которые можно использовать для приближенного расчета частотных характеристик сервоприводов и систем управления по их математическим моделям с незначительными нелинейностями.

метод расчета частотных характеристик замкнутой системы

Вначале приведем метод расчета частотных характеристик замкнутой системы. Для переходной характеристики, заданной в конечном интервале времени [0, t _max], связь переходной характеристики Х ( t ) с АЧХ и ФЧХ при единичном ступенчатом воздействии и замене кривой переходной характеристики отрезками ломаной линии через равные промежутки времени, и с учетом того, что производная на каждом из них постоянна, дается известными выражениями [1–7]:

Φ( j ω) = С (0) + P (ω) + jQ (ω);

P (ω) =    Σ (β (cos(ω t ) – cos(ω t ));

ω i = 1 ^{i             i                 i –1}

Q (ω) =    Σ ⁿ (β (sin(ω t ) – sin(ω t ));

ω i = 1 ^{i             i                  i –1}

e i =

A X ( t )

∆ t

= X '( t ) = const;

A (го) = V P (го) ² + Q (го) ² ;

y(re) при Q (re) > 0 и P (re) < 0;

-n + y( n , l ) при Q (re) <0 и P (re) < 0;

ф(re) = \ -п+у( n , l ) при Q (re)<0 и P (re)>0;

-2п +у( n , l ) при Q (re) >0 и P (re)>0;

n[-1 - 0,5sign P (re)] при Q (re) = 0;

ф(го) = arctg[ P (го)/Q (го)], где С(0) — постоянная составляющая; P (го) — действительная составляющая первой гармоники частотной характеристики замкнутой системы; Q(го) — мнимая составляющая первой гармоники частотной характеристики замкнутой системы; А (го) — амплитуда; ф(го) — фазовое запаздывание; t — время; го — круговая частота (го = 2пf, где f — частота).

Для расчета ЛАЧХ используется выражение A L (го) = 8,68ln[ A (го)], а для расчета ФЧХ в градусах используется выражение Ф°(го) = 57,295ф(го).

В этом случае передаточная функция замкнутой системы определяется как

" ( s )

^{Ф ( s} ) = 1 + " ( s ) " _х( s ) •

Пусть передаточная функция звена цепи обратной связи представляет собой в общем виде апериодическое звено первого порядка

K

" (s) = • ocV 7 тs + 1

Такие цепи обратной связи содержат фильтр высоких частот и применяются для повышения быстродействия сервопривода или системы управления.

Тогда передаточную функцию замкнутой системы можно определить как

Ф( s ) =

" ( s )

^{1 +} V+r " ( s )

После несложных преобразований

Ф( s ) 11 +

K

__oc т s + 1

" ( s )

= " ( s );

K

ф( s )+ т^ " ( s )ф( s )= " ( s );

методы расчета частотных характеристик разомкнутой системы

Алгоритмы размыкания замкнутых сервоприводов и систем управления определяются передаточными функциями звеньев, стоящих в цепях обратной связи.

Пусть система управления представляет собой звено с передаточной функцией W ( s ), замкнутое отрицательной обратной связью, в цепи которого стоит звено с передаточной функцией W _ос( s ). Структурная схема такой системы представлена на рис. 1.

" ( s )l 1 -

K W т s + 1 )

= Ф( s ),

получаем передаточную функцию разомкнутой системы

" ( s )

или

ф( s )

K ос ^ф ( s ) т s + 1

( ) =    ^ф ( s )(т s ₊ 1)

^S    T s + 1- к _эсФ( s ) •

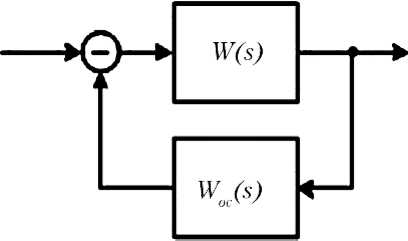
Рис. 1. Структурная схема замкнутой системы управления

Далее, после подстановки в формулу (1) Ф( 5 ) = Ф( ;' го) = P (го) + jQ (го), и учитывая, что 5 = j го, а также то, что W ^( 5 ) = I V(j' го), имеем

[ P (ю) + jQ (ю)](т j ® + 1)

⁽ j ^{ю )}    Tj ю + 1 - к _ОС P (ю) - к _ЭС jQ (ю) • ⁽ )

После преобразований выражения (2)

" ( j го) =

P (го)т j го + P (го) - Q (го)тго + jQ (го) [1 - K _ос P (го)] - j [ K _ос Q (го) - тго]

№ ( jto) =

[ P ( ю ) т J to + P (to) - Q (to)Tto + jQ (to)][1 - К _OC P (to) + jK _3C Q (to) - T j to]

[1 - К ос P (to)]² + [ К ос Q (to) - Tto]²

окончательно получаем

№ ( jto) =

P (to) - К _OC P (to)² - К _OC Q (to)² + P (to)T²to²

Q (to) - P (to)²Tto - К _ос Q (to)²Tto + Q (to)Tto²

[1 - К ос P (to)] ² + [ К ос Q (to) - Tto]²

[1 - К ос P (to)]² + [ К ос Q (to) - Tto]²

.

Тогда передаточную функцию разом кнутой системы можно представить как

W(j' го) = U (го) + jV (го),

-

Q (to)

^{V ( to )}    [1 - К ос P (to)]² + К Oc Q (to)² •

где U (го)

действительная составляю-

щая первой гармоники частотной характеристики разомкнутой системы; V (го) — мнимая составляющая первой гармоники частотной характеристики разомкнутой системы, определяемые как

U (to) =

P (to) - КP (to)² - К _OC Q (to)² + P (to)T²to²

[1 - К ос P (to)]² + [ К ос Q (to) - Tto]²

; (3)

в) K _ос = 1 и т = 0.

Это случай т. н. единичной обратной связи. Здесь передаточная функция звена цепи обратной связи принимает вид

W oc ( s ) = 1.

Из выражений (3) и (4) после подстановки K ос = 1 и т = 0 имеем

U (to) =

V (to) =

Q (to) - P (to)²Tto - К _ос Q (to)²Tto + Q (to)Tto^;

P (to) - P (to) ² - Q (to) ² ;

[1 - P (to)] ² + Q (to)² ’

[1 - К ос P (to)]² + [ К ос Q (to) - Tto]²

Теперь рассмотрим некоторые частные случаи.

а) K _ос = 1.

В этом случае передаточная функция звена цепи обратной связи принимает вид

№ ( s ) = ——•

°^{cV 2} T s + 1

Из выражений (3) и (4) после подстановки K _oc = 1 имеем

P (to) - P (to) ² - Q (to) ² + P (to)T ² to ²

U (to) =--------------------------------

[1 - P (to)] ² + [ Q (to) - Tto] ²

;

Q (to) - P (to) ² Tto - Q (to) ² Tto + Q (to)T ² to ²

V(to) =----------------------------------

[1 - P (to)] ² + [ Q (to) - Tto] ²

.

б) т = 0.

В этом случае передаточная функция звена цепи обратной связи принимает вид

W _oc( s ) = K _oc.

Из выражений (3) и (4) после подстановки т = 0 имеем

U (to) =

P (to) - К oc P (to)² - К oc Q (to)²

[1 - К ос P (to)] ² + КQ( to)²   ’

V (to) =

Q (®)

[1 - P (to)] ² + Q (to) ² •

Для

всех рассмотренных

передаточной функции звена

случаев цепи

обратной связи АЧХ разомкнутой системы определяется как

B(^) = ^ U(my + V (to) ² ,

а ФЧХ — выражениями

д(го) при V (го) >0 и U (ro) < 0;

• -n + 3( n , I ) при V (го) <0 и U (го) < 0;

0(го) = < -п + 3( n , L ) при V (го) <0 и U (го) > 0;

• -2п+3( n , L ) при V (го) >0 и U (го) > 0;

п[-1 - 0,5sign U (го)] при V (го) = 0;

0(го) = arctg[ U (го)/ V (го)].

Для расчета ЛАЧХ разомкнутой сис темы используется уравнение

BL (го) = 8,68ln[ B (го)], а для расчета ее ФЧХ в градусах исполь зуется выражение

6°(го) = 57,2959(го).

-

-

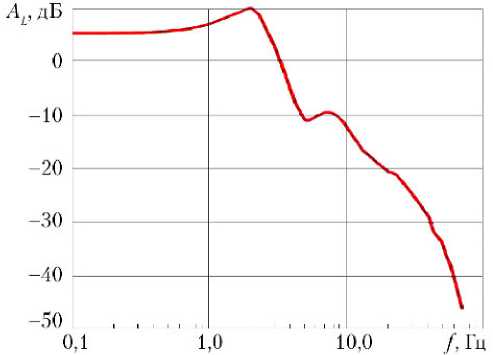
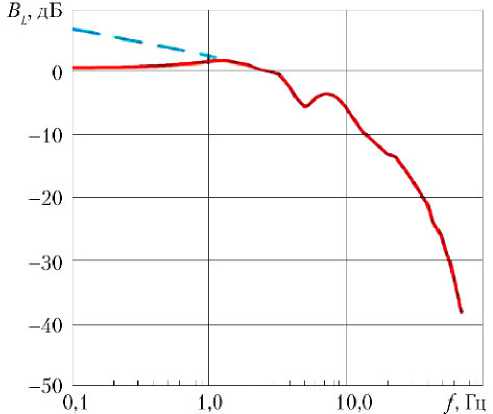
Результаты расчетов ЛАФЧХ рулевого тракта системы управления вектором тяги разгонного блока, выполненного по его переходной характеристике, приведенной на рис. 2, в соответствии с разработанным методом, представлены на рис. 3 и 4.

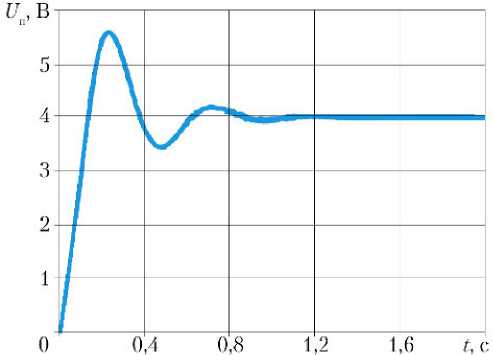
Рис. 2. Переходная характеристика замкнутого рулевого тракта

a)

a)

б)

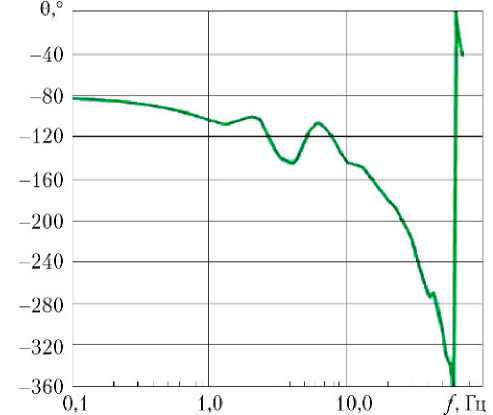
Рис. 4. Логарифмические амплитудно-частотные характеристики (а) и фазовые частотные характеристики (б) первой гармоники разомкнутого рулевого тракта

б)

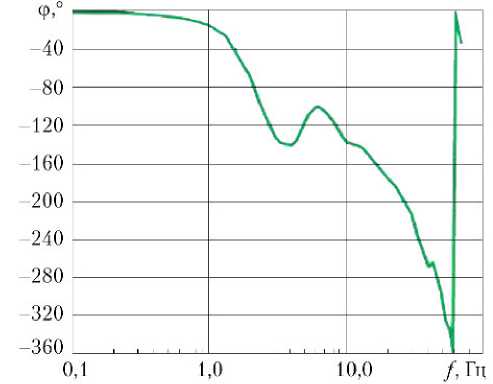
Рис. 3. Логарифмические амплитудно-частотные характеристики (а) и фазовые частотные характеристики (б) первой гармоники замкнутого рулевого тракта

Для вычисления переходной характеристики замкнутого рулевого тракта, представленной на рис. 2, использовалась его упрощенная математическая модель, приведенная в работе [8]. В этой работе упрощенная математическая модель рулевого тракта представляет собой математическую модель рулевой машины с двухдроссельным электрогидравлическим усилителем, замкнутую отрицательной обратной связью в виде апериодического звена первого порядка.

На рис. 4, а в низкочастотной области неявно выражен наклон 20 дБ на декаду. Канонический вид ЛАЧХ в низкочастотной области показан на этом рисунке пунктирной линией. Это отличие объясняется влиянием нелинейности математической модели рулевого тракта.

Сравнение полученных результатов расчетов с результатами расчетов частотных характеристик рулевого тракта по той же математической модели, полученными двухканальным моногармони-ческим методом, показало возможность приближенного расчета частотных характеристик для предварительной оценки запасов устойчивости по амплитуде и фазе. Кроме этого, автором проведена с положительными результатами апробация методов расчета частотных характеристик разомкнутого рулевого тракта для частных случаев звена цепи обратной связи.

заключение

Разработаны методы расчета частотных характеристик разомкнутых сервоприводов и систем управления с использованием частотных характеристик замкнутых сервоприводов и систем управления по их линейным или линеаризованным математическим моделям, которые можно использовать для приближенного расчета частотных характеристик сервоприводов и систем управления по их математическим моделям с незначительными нелинейностями.

Выведены уравнения для расчета частотных характеристик разомкнутых сервоприводов и систем управления для частных случаев передаточной функции цепи обратной связи.

Исследована работоспособность разработанных методов расчета частотных характеристик разомкнутых сервоприводов и систем управления.

Разработанные методы позволяют за один счет получать частотные характеристики как замкнутого, так и разомкнутого сервопривода (как замкнутой, так и разомкнутой системы управления).