Методы синтеза квазиклеточных сетей

В работах [1,2] рассмотрены квазиклеточные сети как фундаментальные дискретные структуры, не имеющие сигнатуры (рис. 1). Основным предназначением указанных дискретных структур является реализация проектирования и моделирования систем, сводящихся к рассмотрению потоков при различных предметных интерпретациях. Изначально представление о квазиклеточной сети было дано на основе некоторых преобразований графа, являющегося двусортным множеством, т. е. обладающий носителем и сигнатурой. В отличие ряда дискретных структур, в т.ч. графов, квазиклеточные сети не обладают сигнатурой, поэтому не следует считать базовый граф квазиклеточной сети обязательным по определению.

Рис. 1. Базовый граф и построенная на его основе квазиклеточная сеть.

Однако, синтез квазиклеточной сети на основе базового графа следует рассматривать как один из методов синтеза – метод базового графа. Метод базового графа позволяет построить динамическую структуру, реализуемую для ЭВМ и пригодную для микромоделирования и макромоделирования потоков в сетях. При этом, следует отметить, что распространённые дискретные структуры[3] предполагают рассмотрение потока в сети как единого объекта, т. е. рассмотрение только на макроуровне. Таким образом, метод базового графа фактически позволяет синтезировать динамическую структуру на базе статической.

Следует рассмотреть ряд методов синтеза квазиклеточных сетей, не зависящих от базовых графов. Такие методы фактически сводятся к расстановке клеток и их координат.

Первый метод, который будет рассмотрен – метод битого клеточного автомата. В работах[1,2] было показано, что квазиклеточная сеть обладает схожими свойствами с клеточными автоматами. Фактически, клеточный автомат представляет собой растровую структуру, в которой каждая точка пространства соответствует клетке, в то время как в квазиклеточных сетях клеточный автомат является одним из элементов, который может располагаться в любой части пространства (рис. 2).

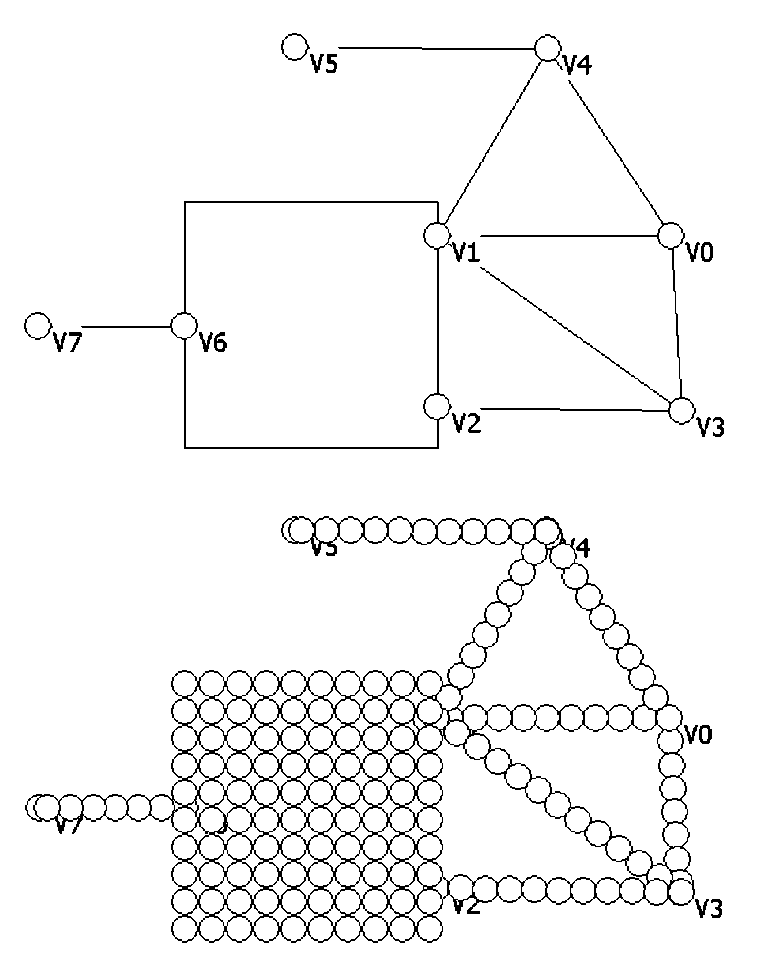
Рис. 2 Клеточный автомат в составе квазиклеточной сети.

Следует отметить, что клеточный автомат соответствует определению квазиклеточной сети[4], однако с точки зрения топологии существенно отличается от квазиклеточных сетей, рассмотренных выше. Поскольку клеточный автомат соответствует определению квазиклеточной сети и вкрапления клеточного автомата являются её компонентами, то структура образованная некоторыми клетками клеточного автомата также может считаться квазиклеточной сетью (рис. 2).

Пусть имеем сколь угодно большой элемент клеточного автомата, каждая клетка которого:

^Q i ) = ^{( X} y ^,y y ^,S y ) .

Рассмотрим подмножество ^{Qij '} , для которого справедливо:

Q jK ⁾' e Q jK ⁾

Q * K ) ' *0 .

ij

Фактически, речь идёт об удалении из множества клеток, образующих клеточный автомат, части элементов. Это позволяет синтезировать квазиклеточную сеть на базе клеточного автомата (рис. 3). Описанный подход к синтезу, предполагающий удаление части клеток клеточного автомата называется методом битого клеточного автомата.

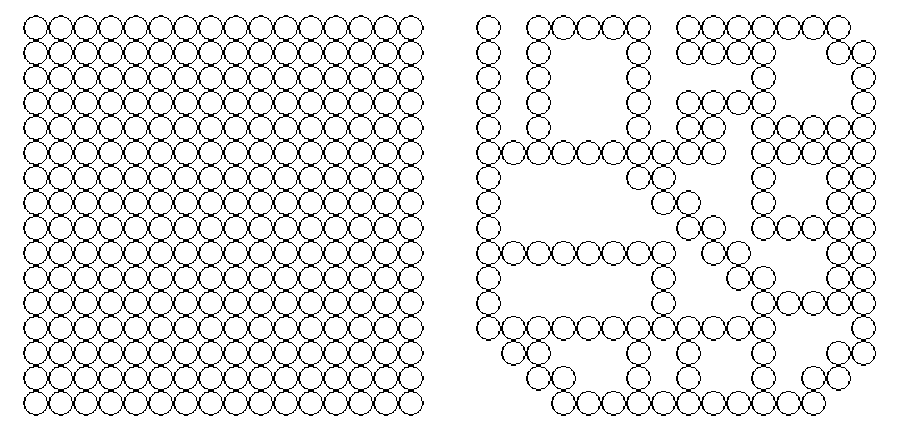
Рис. 3 Клеточный автомат и квазиклеточная сеть, синтезированная методом битого клеточного автомата.

Каждый из рассмотренных выше методов синтеза квазиклетоных сетей обладает некоторыми специфическими особенностями. Метод базового графа предполагает наличие дискретной структуры, представляющей собой двусортное множество. Преимуществом такого метода является возможность добавления динамики в статичные дискретные структуры. С другой стороны, такой метод обязательно требует наличие графа, который в отличие от квазиклеточной сети является двусортным множеством. Метод битого клеточного автомата позволяет синтезировать квазиклеточную сеть на базе клеточного автомата путём исключения некоторых его элементов. Рассмотренные методы так или иначе затрагивают другие ранее известные дискретные структуры и в результате некоторых манипуляций над ними позволяют получить квазиклеточные сети, соотвествтующие определению.

Рассмотрим метод, в основе которого лежит синтез квазиклеточных сетей без использования других дискретных структур. Основу метода составляет специальный микрообъект, параметрами которого являются топологические координаты ^x c ^{, y}c . Назовём микрообъект генерирующей фишкой или генерирующей клеткой. Рассматриваемый микрообъект на каждой итерации совершает перемещение на величины Δ ^xci^, Δ ^yci соответственно по осям ^{x, y} . Тогда для координат на каждой итерации справедливо:

xci + 1= xci + ^xci ,(4)

ycl+1 = Уа + ДУ«(5)

На каждой итерации происходит формирование клетки квазиклеточной сети в координатах генерирующей фишки:

Q,=(x№y.,,S,)(6)

Стоит отметить, что для того, чтобы расположение формируемых клеток удовлетворяло определению квазиклеточной сети, требуется, чтобы расстояние между координатами генерирующей фишки x ci , yci и xci +i ,yci+i на соседних итерациях не превышало величину 2R , установленную для квазиклеточной сети, т.е фактически, расстояние между соседними клетками не должно превышать 2R : Д2 xcl+Д2 ycl < 4R2

.

Невыполнение условия (7) приведёт к невозможности циркуляции в квазиклеточной сети и появлению клеток, не имеющих соседних.

Стоит обратить внимание на то, что условие (7) имеет вид неравенства. Также по определению квазиклеточной сети не требуется строгого касания круговых областей, а возможен вариант с их пересечением. Однако, метод синтеза, рассмотренный выше и основанный на динамике микрообъекта – генерирующей фишки позволяет формировать квазиклеточные сети не имеющие пересечений клеток. В такой ситуации требуется, чтобы д2xci+Дyci=4r2 .                               (8)

Рассмотренные ранее методы синтеза квазиклеточных сетей, такие как метод базового графа и метод генерирующей фишки при условии (8) допускали пересечение клеток. Однако, метод генерирующей фишки позволяет синтезировать квазиклеточные сети, в которых не возникнет пересечения клеток. Тогда, для достижения указанного свойства, каждая клетка

Q i = ( x ci ,y ci^,Si )

должна отвечать не только условию (8), но и:

^V j : 7 ( x ci - x j ^{) 2} +⁽ y_ci - Уз ^{) 2} = 4R 2 .

Также стоит отметить, что значительную роль играет зависимость величин Δxci , Δyci на каждой итерации. Фактически речь идёт о зависимостях вида:

:

^xci = Ax( i ) Л У a = Ay(i)

Рассматривая (11) с точки зрения кинематики материальной точки, получаем зависимости для проекций скорости генерирующей фишки.

Тогда закон движения генерирующей фишки примет вид:

[x c ⁽ i ⁾⁼ J ^A x ⁽ i ) di

[ Ус ( i )=J ^y ( i ) di

Таким образом, метод генерирующей фишки позволяет синтезировать квазиклеточные сети, не опираясь не какие-либо дополнительные дискретные структуры. Кроме того, полученные квазиклеточные сети позволяют решить проблему пересечения клеток, что возникает при использовании метода базового графа. Стоит также отметить, что метод генерирующей фишки фактически направлен на синтез квазиклеточной сети для объектов для которых известны траектории движения.

Фактически синтез указанным методом предполагает обучение и настройку квазиклеточной сети в соответствии с движением объектов. Так, при рассмотрении однотипного движения большого количества объектов, предполагается наличие некоторого набора заранее известных траекторий, на базе которых формируется квазиклеточная сеть, предназначенная для моделирования динамики большого количества однотипных объектов.

Таким образом, рассмотрены методы синтеза квазиклеточных сетей, основанные на различных подходах, основанных как на анализе структуры, так и на получении требуемых их динамических свойств.