Методы статического анализа двухприводной электромеханической рулевой машины жидкостного ракетного двигателя

Рациональный выбор значений параметров электромеханических рулевых машин (РМ), получивших широкое распространение в системах управления вектором тяги (СУВТ) жидкостных ракетных двигателей космических кораблей, может быть достигнут путём проведения системного анализа и параметрической оптимизации.

Составляющими элементами системного анализа РМ являются методы статического анализа, включающие методы расчёта статических характеристик, к которым относятся:

• •    моментная характеристика РМ, т. е. зависимость моментов, развиваемых выходным валом РМ, от командного сигнала в виде напряжения постоянного тока;

• •    семейство регулировочных характеристик РМ, т. е. зависимостей угловых

скоростей движения выходного вала РМ от командного сигнала в виде напряжения постоянного тока и суммарной преодолеваемой нагрузки.

В процессе расчётов статических характеристик вычисляются некоторые дополнительные зависимости параметров, такие как, например, семейства зависимостей токов, потребляемых магнитоэлектрическими двигателями (МЭД) РМ от командного сигнала в виде напряжения постоянного тока и суммарной преодолеваемой нагрузки.

Статический анализ РМ позволяет определить граничные значения параметров эксплуатации РМ при её различных алгоритмах управления в составе СУВТ.

Постановка задач исследований

В настоящей работе ставятся следующие задачи:

• •    разработка итерационных методов статического анализа РМ;

• •    разработка динамического метода статического анализа РМ;

• •    расчёт статических характеристик РМ;

• •    исследование влияния разброса характеристик МЭД на статические характеристики РМ.

Математическая модель динамического режима работы рМ

Математическая модель	динамичес-
кого режима работы РМ,	согласно
источникам [1, 2], включает в себя
следующие уравнения:
dI 1
dt = b 1 U – b 2 I 1 – b 3 ω ;	(1)
dI
dt = b 1 U – b 4 I 2 – b 5 ω ;	(2)
d ϕ
dt = ω ;	(3)
d ω
dt = b 6 I 1 + b 7 I 2 – b 8 M c .	(4)

Здесь b₁ – b₈ — комплекс постоянных коэффициентов:

• b ₁ = 1/ L ; b ₂ = R ₁ / L ;

• b ₃ = K _э1 / L ; b ₄ = R ₂ / L ;

• b ₅ = K _э2 / L ; b ₆ = K _м1 / J ;

• b 7 = K м2 / J ; b 8 =1/ J ,

где L — индуктивность обмоток электрической цепи; R ₁ — активное сопротивление электрической цепи первого МЭД; R ₂ — активное сопротивление электрической цепи второго МЭД; U — напряжение питания, подаваемое на МЭД; K _э1 — коэффициент электромагнитной скоростной связи первого МЭД; K _э2 — коэффициент электромагнитной скоростной связи второго МЭД; I ₁ — ток, потребляемый первым МЭД; I ₂ — ток, потребляемый вторым МЭД; ω — угловая скорость вращения валов обоих МЭД, соединённых с общим редуктором; М _с — полный момент сопротивления, приведённый к валам МЭД; ϕ — угол поворота валов обоих МЭД; K _м1 — коэффициент моментной характеристики первого МЭД; K _м2 — коэффициент моментной характеристики второго МЭД; J — момент инерции вращающихся частей РМ, приведённый к валам МЭД.

Угол поворота выходного вала редуктора РМ определяется как

α = 57,295( ϕ / i _р ),

• а    его угловая скорость:

γ = 57,295( ω / i _р ),                        (5)

где i _р – передаточное число редуктора РМ.

Момент инерции, приведённый к валам МЭД, для двухприводной РМ определяется следующей формулой [2]:

J = 2 J _д + J ₁ / i ₁ ² + J ₂ /( i ₁ ² i ₂ ² ) + J ₃ /( i ₁ ² i ₂ ² i ₃ ² ) +

+ J4/(i12i22i32i42) + 2J5/(i12i22i32i52) + J6 /(i12i22i32i62), где Jд — момент инерции ротора МЭД; J1 — момент инерции шестерни первой ступени редуктора; i1 — передаточное число первой ступени редуктора; J2 — момент инерции шестерни второй ступени редуктора; i2 — передаточное число второй ступени редуктора; J3 — момент инерции шестерни третьей ступени редуктора; i3 — передаточное число третьей ступени редуктора;

J4 — момент инерции шестерни четвёртой ступени редуктора; i4   — передаточное число четвёртой ступени редуктора; J5 — момент инерции шестерни, соединяющей третью ступень редуктора с дискретными датчиками угла (ДДУ); i5 — передаточное число передачи от третьей ступени редуктора к валу ДДУ; J6 — момент инерции шестерни, соединяющей третью ступень редуктора с телеметрическим потенциометром (ТП) с учётом момента инерции подвижных частей ТП; i6 — передаточное число передачи от третьей ступени редуктора к валу ТП.

Полный момент сопротивления М _с , приведённый к валам МЭД, определяется следующим выражением [2]:

М _с = М _с.э1 + М _с.э2 + ( М _н + 2 М _к.к )/( i _р η _р ) +

+ 2Мд.д.у/(iр1ηр) + Мт.п/(iр2ηр), где Мс.э1, Мс.э2 — моменты сухого трения в МЭД; Мн — момент нагрузки на выходном валу РМ; Мк.к — момент сухого трения от концевых контактов; ηр — КПД редуктора и других передач от валов МЭД к валу ТП и от валов МЭД к валам ДДУ, определяемое как ηр = η1η2η3η4, где η1–η4   — КПД каждой ступени; Мд.д.у и Мт.п – моменты, приведённые к валам ДДУ и ТП соответственно; iр — передаточное число редуктора РМ, определяемое как iр = i1i2i3i4; iр1 — передаточное число передачи от валов МЭД к валам ДДУ, определяемое как iр1 = i1i2i3i5; iр2 — передаточное число передачи от валов МЭД к валу ТП, определяемое как iр2 = i1i2i3i6.

Математические модели статического режима работы рулевой машины

В основу разработки математических моделей статических режимов работы рулевых машин, а также методов расчёта их статических характеристик, были положены:

• •    математическая модель магнитоэлектрического двигателя [1];

• •    математическая модель динамического режима работы двухприводной электромеханической РМ [2];

• •    математические модели электроприводов и электромеханических систем [3–7];

• •    модификация метода Зейделя для решения систем нелинейных алгебраических и трансцендентных уравнений [8].

Математические модели статических режимов работы РМ получаются из дифференциальных уравнений динамических режимов работы РМ (1)–(4) путём приравнивания к нулю их старших производных.

Математическая модель статического режима работы и итерационный метод расчёта моментной характеристики рулевой машины

Моментную характеристику РМ определяют при условии предположения о заторможенном выходном вале РМ, т. е. об отсутствии вращения валов МЭД и выходного вала РМ ( ω = 0; γ = 0).

• I1    = U/R1;(6)

• I2    = U/R2;(7)

Kм1I1 + Kм2I2 – Mс = 0.(8)

Отрицательные значения момента М , развиваемого выходным валом РМ, полагаются равными нулю, поскольку в этих случаях выходной вал РМ не развивает движущего момента. В связи с этим уравнение (8) преобразуется к виду:

при ∑М ≤ 0 → Мэ = 0, а при ∑М > 0 → Мэ = ∑М, где Мэ — момент, развиваемый валами МЭД; ∑М — суммарный момент на валах МЭД, определяемый как

∑ М = K м1 I 1 + K м2 I 2 – M с .              (10)

Тогда момент, развиваемый выходным валом РМ, определяется выражением

М = М _э i _р η _р .                            (11)

Уравнения (6), (7), (9), с учётом (10) и (11), образуют систему, описывающую математическую модель двухприводной РМ для расчёта её моментной характеристики.

Итерационный метод расчёта моментной характеристики рулевой машины заключается в последовательном решении нелинейной системы алгебраических уравнений (6), (7), (9), с учётом выражения (10), методом, изложенным в работе [8], при изменении командного сигнала в виде напряжения постоянного тока, подаваемого на МЭД РМ, от U = 0 до U = U _max с шагом напряжения h_u , где U _max — максимальное значение напряжения, подаваемого на МЭД из эксплуатационного диапазона, с последующим вычислением моментов, развиваемых валами МЭД по выражению (9), выходным валом рулевой машины по выражению (11) и суммарного тока ∑ I , потребляемого МЭД РМ, по выражению

∑ I = I ₁ + I ₂ . (12)

В процессе расчётов статических характеристик рулевой машины итерационными методами, при входе в итерационный процесс на каждом следующем шаге по командному сигналу в виде напряжения постоянного тока, подаваемого на МЭД РМ, в качестве начальных значений вычисляемых параметров используются значения этих параметров, полученные на предыдущем шаге.

Для расчёта моментной характеристики варианта эксплуатации РМ с одним функционирующим МЭД достаточно приравнять нулю коэффициент моментной характеристики второго МЭД, т. е. K _м2 = 0, выходным параметром математической модели РМ считать только ток I ₁ , потребляемый первым МЭД, а при вычислении суммарного тока, потребляемого МЭД РМ, значение тока второго МЭД I ₂ полагать равным нулю.

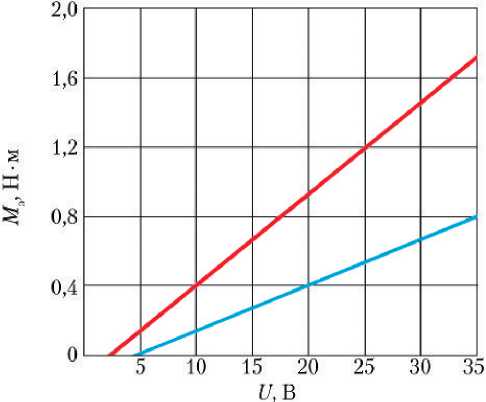
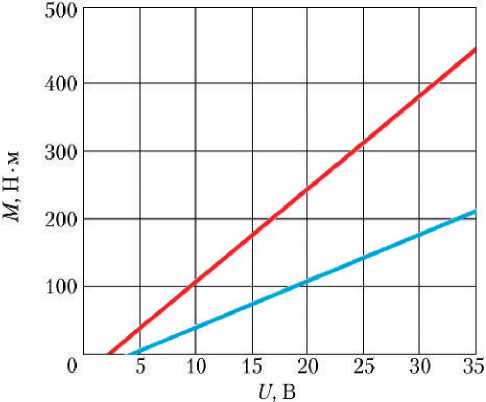
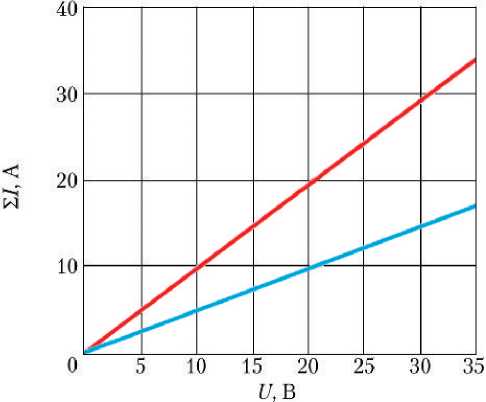
Результаты расчёта статических характеристик РМ при заторможенном вале, а именно: моментных характеристик, т. е. зависимостей моментов, развиваемых МЭД РМ, моментов, развиваемых самой РМ и зависимостей суммарного потребляемого тока РМ от командного сигнала в виде напряжения постоянного тока, подаваемого на МЭД РМ, — для режимов работы РМ с двумя МЭД и с одним МЭД представлены на рис. 1.

а)

б)

в)

Рис. 1. Статические характеристики РМ при заторможенном вале для режима работы: ^™ — с двумя МЭД; ^™ — с одним МЭД; а — зависимости моментов, развиваемых МЭД, от командного напряжения; б — зависимости моментов, развиваемых валом РМ, от командного напряжения; в — зависимости суммарных токов, потребляемых МЭД, от командного напряжения

Математическая модель статического режима работы и итерационный метод расчёта регулировочной характеристики рулевой машины

Приравнивая к нулю производные в уравнениях (1), (2) и (4) и исключая из этих уравнений параметры L и J , получаем уравнение (8) и следующие уравнения:

U – R ₁ I ₁ – K _э1 ω = 0;                   (13)

U – R ₂ I ₂ – K _э2 ω = 0.                   (14)

Поскольку в уравнение (8) параметр ω не входит в явном виде, необходимо применить искусственный приём, заключающийся во введении в уравнение (8) дополнительного члена в виде вязкого трения с очень малым значением коэффициента вязкого трения K _ω . Значение этого коэффициента подбирается экспериментально для каждой конкретной математической модели.

Переписываем уравнение (8) в виде

Kм1I1 + Kм2I2 – Mс – Kωω = 0.(15)

Разрешая уравнения (13),  (14) и

(15) относительно искомых параметров, переписываем их в следующем виде:

I1 = U/R1 – (Kэ1 /R1)ω;(16)

I2 = U/R2 – (Kэ2 /R2)ω;(17)

ω =(Kм1/Kω)I1+(Kм2/Kω)I2– Mс/Kω.(18)

Вводим комплекс постоянных коэффициентов

a 1 =	U / R 1 ;       a 2 = K э1 / R 1 ;	a 3 = U / R 2 ;
a 4 =	K э2 / R 2 ;    a 5 = K м1 / K ω ;	a 6 = K м2 / K ω ;
a 7 =	M с / K ω и подставляем	их в урав-
нения	(16)–(18):
I 1 =	a 1 – a 2 ω ;	(19)
I 2 =	a 3 – a 4 ω ;	(20)
ω =	a 5 I 1 + a 6 I 2 – a 7 .	(21)

По аналогии с методом расчёта моментной характеристики, отрицательные значения момента М, развиваемого выходным валом РМ, полагаются равными нулю, поскольку в этих случаях выходной вал РМ не развивает движущего момента. В связи с этим уравнение (21) также преобразуется к виду:

при ∑М ≤ 0 → ω = 0, а при ∑М > 0 → ω = ∑М, где суммарный момент на валах МЭД ∑М определяется как

Σ М = a ₅ I ₁ + a ₆ I ₂ – a ₇ .                   (23)

Итерационный метод расчёта регулировочной характеристики РМ заключается в последовательном решении нелинейной системы уравнений (19), (20), (22) с учётом выражения (23) методом, изложенным в работе [8], при изменении командного сигнала в виде напряжения постоянного тока, подаваемого на МЭД РМ, от U = 0 до U = U _max с шагом напряжения h_u , где U _max — максимальное значение напряжения, подаваемого на МЭД из эксплуатационного диапазона, с последующим вычислением угловой скорости вращения вала РМ по выражению (5) и суммарного тока, потребляемого МЭД РМ, по выражению (12).

Для расчёта регулировочной характеристики варианта эксплуатации РМ с одним функционирующим МЭД достаточно приравнять к нулю коэффициент моментной характеристики второго МЭД, т. е. K _м2 = 0, а выходным параметром математической модели РМ считать только ток I ₁ , потребляемый первым МЭД. При вычислении суммарного тока, потребляемого МЭД РМ, значение тока второго МЭД I ₂ нужно полагать равным нулю.

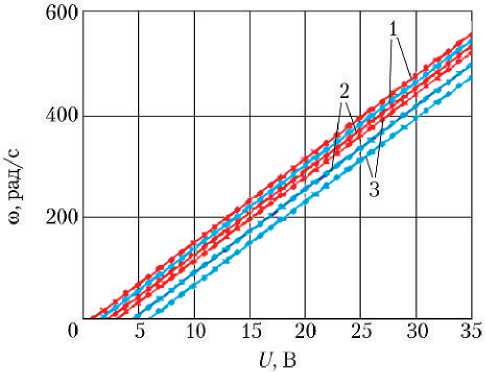
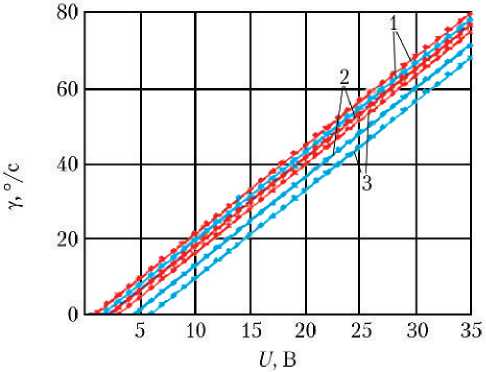
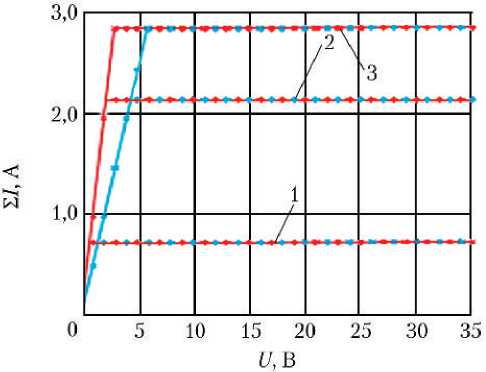
Результаты расчёта статических характеристик РМ, а именно: зависимостей угловых скоростей вращения валов МЭД, регулировочных характеристик РМ и зависимостей суммарного потребляемого тока МЭД РМ от командного сигнала в виде напряжения постоянного тока, подаваемого на МЭД РМ, для трёх значений момента на выходном вале РМ для режимов работы РМ с двумя МЭД и одним МЭД — представлены на рис. 2.

а)

динамический метод

«автоинтегрирования» расчёта регулировочных характеристик рМ

б)

в)

Рис. 2. Статические характеристики РМ для режимов работы с двумя МЭД и одним МЭД: а — зависимости угловых скоростей вращения валов МЭД от командного напряжения; б — регулировочные характеристики РМ; в — зависимости суммарного потребляемого тока МЭД от командного напряжения; 1 — М н = 5 Нм; 2 — М н = 25 Нм; 3 — М н = 35 Нм; ^™ — расчёт итерационным методом режимов работы с двумя МЭД; ^™ — расчёт итерационным методом режима работы с одним МЭД; ♦♦♦ — расчёт динамическим методом режима работы с двумя МЭД; ♦♦♦ — расчёт динамическим методом режима работы с одним МЭД

Для верификации разработанных итерационных методов расчёта регулировочной характеристики РМ был разработан специальный динамический метод «автоинтегрирования». Изначально этот метод применялся для определения амплитудно-фазовых частотных характеристик динамических объектов [9].

Сущность разработанного динамического метода расчёта регулировочных характеристик РМ заключается в том, что процессы численного интегрирования системы нелинейных дифференциальных уравнений математической модели РМ при каждом фиксированном значении входного командного сигнала в виде напряжения постоянного тока, подаваемого на МЭД РМ, продолжаются до тех пор, пока среднее значение угловой скорости выходного вала РМ не станет достаточно постоянным.

Алгоритм метода имеет два основных цикла: по величине входного командного сигнала и по времени. При этом расчёте регулировочной характеристики РМ анализируемым параметром является средняя угловая скорость вращения валов МЭД ω _с .

Для уменьшения влияния переходных процессов на результаты расчётов наиболее предпочтительным является принцип сравнения среднего значения анализируемого параметра за последние n–k шагов интегрирования h на последнем шаге n со средним значением этого параметра за последние n–k –1 шагов на предпоследнем n –1 шаге, где n — номер последнего шага интегрирования, а k — число первых, не анализируемых шагов интегрирования, на которых влияние переходного процесса наиболее значительно.

Выбор числа k первых, не анализируемых шагов интегрирования, самого шага интегрирования h и погрешности вычислений ε является предметом оптимизации под конкретную математическую модель РМ с её конкретными параметрами путём поискового моделирования.

Таким образом, в процессе интегрирования системы нелинейных дифференциальных уравнений математической модели РМ проводится вычисление среднего значения угловой скорости валов МЭД РМ ωс:

®^{( N} ) =

n

■ ? 1Ю( г)

г = К +1

n – k

Процесс интегрирования системы нелинейных дифференциальных уравнений математической модели РМ при каждом командном сигнале продолжается до тех пор, пока не будет выполнено неравенство

® c ^{( П}) ® c ^{( П -} 1)

® c ^{( П} )

|-100% С е .

Примечание : при умножении сравниваемых модулей на 100% число ε определяет погрешность вычисления в процентах.

Дополнительно на каждом анализируемом шаге интегрирования при расчёте регулировочных характеристик вычисляется среднее значение суммарного тока I = I ₁ + I ₂ , потребляемого МЭД РМ, по выражению

I _c ( n ) =

S I(i)

г = к +1

п - к где Iс(n) — среднее значение суммарного тока, потребляемого МЭД РМ, на последнем шаге интегрирования n.

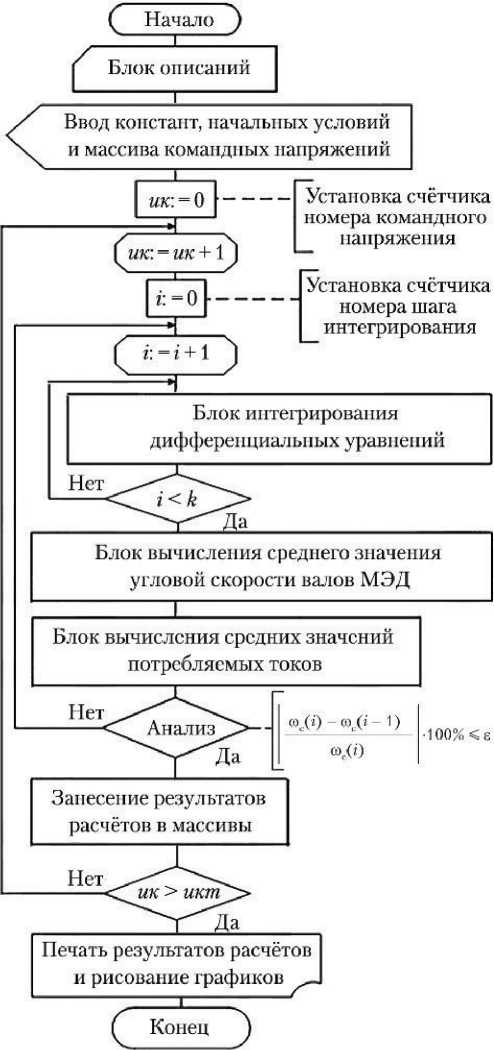
Блок-схема алгоритма разработанного динамического метода «автоинтегрирования» расчёта регулировочной характеристики РМ представлена на рис. 3.

Для выполнения расчётов этим динамическим методом система дифференциальных уравнений математической модели РМ (1)–(4) после введения в неё параметра, определяющего сумму нормированных моментом инерции РМ моментов, развиваемых валами МЭД ∑Мэд, была приведена к виду (1)–(3) и dω при ∑Мэд ≤ 0 →    = 0, dω а при ∑Мэд > 0 →    = ∑Мэд,      (24)

где ∑ М _эд = b ₆ I ₁ + b ₇ I ₂ – b ₈ M _с .

Конец

< Ввод констант, начальных условий и массива командных напряжений

Блок вычисления среднего значения угловой скорости валов МЭД

Блок вычисления средних значений потребляемых токов

Начало )

wk: = ик

Установка счетчика номера шага интегрирования

■100% <8

Нет     ^

——<с wk >  икт

Печать результатов расчётов и рисование графиков -

Установка счётчика номера командного напряжения

«ДО - <0c(i - 1)

Нет

Блок интегрирования дифференциальных уравнений

Занесение результатов расчётов в массивы

Нет

——Анализ^ ^Т^Да

^ Блок описаний ык: = 0

i: = 0 ■

Рис. 3. Блок-схема алгоритма динамического метода статического анализа РМ

Результаты расчётов регулировочных характеристик РМ и зависимостей суммарного потребляемого тока МЭД РМ от командного сигнала в виде напряжения постоянного тока, подаваемого на МЭД РМ, методом «автоинтегрирования» по математической модели (1)–(3) и (24) вместе с результатами расчётов этих характеристик итерационным методом при двух значениях постоянного момента, приложенного к выходному валу РМ, для режимов работы РМ с двумя МЭД и с одним МЭД, также представлены на рис. 1 и рис. 2.

Как видно из рисунков, графики характеристик, рассчитанные обоими методами, имеют хорошее схождение, что подтверждает корректность, а также высокую точность и эффективность разработанных итерационных методов статического анализа и специального динамического метода статического анализа РМ.

исследование влияния разброса скоростной характеристики Мэд на статические характеристики рМ

В соответствии с документацией на МЭД его скоростная характеристика может иметь разброс в диапазоне ±20% от номинального значения при номинальном моменте. Влияние этого явления удобно промоделировать, создавая искусственные характеристики МЭД путём вариации сопротивления электрической цепи МЭД.

На рис. 4 показаны статические характеристики МЭД при номинальном сопротивлении электрической цепи МЭД R = 2,05 Ом и при двух его дополнительных значениях: R = 0,5 Ом и R = 3,0 Ом.

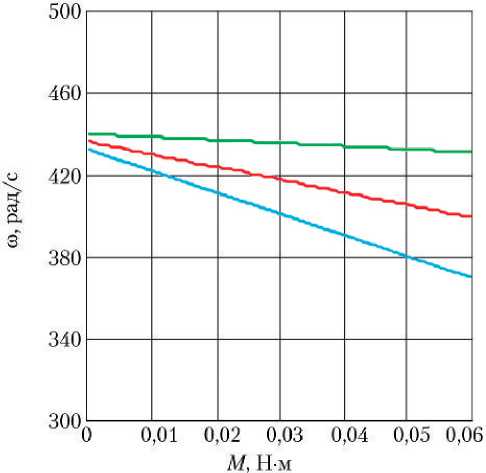
Рис. 4. Статические характеристики МЭД: ^^ —

R = 0,5 Ом; ^ — R=2,05 Ом; ^™ — R=3,0 Ом

Подставляя эти дополнительные значения в математическую модель итерационного метода расчёта регулировочной характеристики (19), (20) и (22), получаем в результате моделирования регулировочные характеристики РМ для одинаковых номинальных сопротивлений электрических цепей МЭД РМ и для их различных значений при номинальном моменте на выходном вале РМ, представленные на рис. 5.

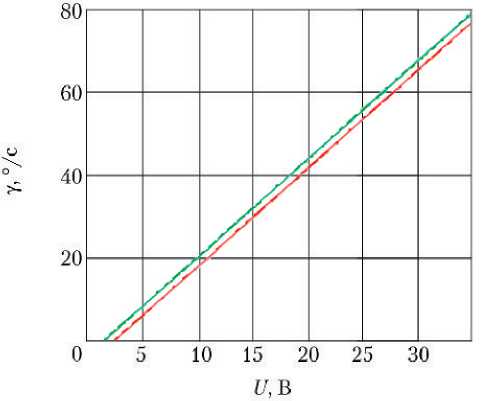
Рис. 5. Регулировочные характеристики РМ: ^^ — неидентичные сопротивления электрических цепей МЭД; ^^ — идентичные сопротивления электрических цепей МЭД

При неидентичности сопротивлений электрических цепей МЭД происходит перераспределение энергии между этими двумя МЭД. Один из МЭД при этом начинает несколько подгружать другой, но регулировочная характеристика РМ при этом располагается несколько выше регулировочной характеристики РМ с идентичными сопротивлениями электрических цепей МЭД.

При расчётах были использованы предельные значения разброса характеристик МЭД. При меньших значениях разброса регулировочные характеристики будут располагаться ещё ближе друг к другу.

Таким образом, можно утверждать, что неидентичность сопротивлений электрических цепей МЭД практически не оказывает влияния на регулировочную характеристику РМ, и её влиянием при моделировании РМ и электромеханической системы управления вектором тяги жидкостного ракетного двигателя можно пренебречь.

заключение

В итоге проведённых разработок получены следующие основные результаты:

• •    разработаны математическая модель статического режима работы и итерационный метод расчёта моментных характеристик электромеханической РМ;

• •    разработаны математическая модель статического режима работы и итерационный метод расчёта регулировочной характеристики электромеханической РМ;

• •    разработан динамический метод «автоинтегрирования» расчёта регулировочных характеристик РМ;

• •    проведена верификация разработанных итерационных методов расчёта регулировочных характеристик рулевой машины динамическим методом «автоинтегрирования»;

• •    исследовано влияние разброса скоростной характеристики МЭД на регулировочную характеристику РМ. Показано, что неидентичность сопротивлений электрических цепей магнитоэлектрических двигателей практически не оказывает значительного влияния на регулировочную характеристику РМ.