Методы теории массового обслуживания при исследовании и оптимизации движения на управляемых перекрёстках

Математическое моделирование транспортных потоков в наше время является весьма актуальным в связи с всё большим увеличением количества автомобилей и ростом инфраструктуры городов. Практически любой путь между двумя точками включает пересечение множества перекрёстков, в том числе управляемых. По этой причине представляет большой интерес не только изучение времени, потерянного при движении в «пробках», но и изучение потерянного времени при пересечении управляемых перекрёстков.

В работе [1] описано, как с точки зрения численных методов было исследовано поведение автомобилей на управляемом перекрёстке. Алгоритм обновления состояния автомобилей для модели, обобщённой на двумерный случай (см. с. 134 со второго по шестой абзац), а также алгоритм прохождения автомобилем перекрёстка (см. с. 134–135) были заимствованы из работы [6]. Автор данной работы приносит благодарности М. А. Трапезниковой, И. Р. Фурманову, Н.Г. Чурбановой и Р. Липпу, не претендует на авторство указанных алгоритмов, а также приносит извинения за некорректное цитирование.

В этой статье в основном используются методы теории массового обслуживания для транспортного моделирования.

Методы массового обслуживания для моделирования задач на перекрёстке использовались в работе [2]. В ней рассматривалась система GI | G |ro , в которой запросы, поступившие на одном периоде занятости, имеют одинаковое время обслуживания. Времена обслуживания на различных периодах занятости — независимые одинаково распределенные случайные величины. Эта модель возникла при описании «синхронного движения», возникающего в транспортных системах при высокой интенсивности движения. С помощью рассматриваемой модели авторы получили распределение времени ожидания автомобиля на однополосной второстепенной дороге при пересечении главной и второстепенной дорог на неуправляемом перекрестке, если в момент его появления на перекрестке нет других автомобилей. По сути, движение на неуправляемом перекрёстке можно сформулировать как задачу о регулируемом перекрёстке с пуассоновскими длинами фаз. Аналогичные методы рассматривались также в [3].

При рассматривании светофора с фиксированными длительностями фаз возникает более сложный математический аппарат. В частности, данная задача, правда, для случая одной однополосной дороги и светофора с двумя фазами (зелёный-красный), была рассмотрена в [4].

Cледует отметить, что зачастую существующие как макро-, так и микромодели рассматривают только движение по однополосным трассам. Применение методов теории массового обслуживания к транспортным задачам на многополосных дорогах практически не осуществлялось. В исследовании данных задач необходимо учитывать, что время обслуживания на многополосных перекрёстках – величина, зависящая от текущей светофорной фазы и распределения целей движущихся АТС.

Для того чтобы полученные результаты можно было использовать, необходимо с помощью вышеуказанных методов изучить влияние длительностей светофорных фаз и светофорных режимов на такие величины, как средняя пропускная способность на перекрёстке, среднее время ожидания, длина скапливаемых очередей по различным направлениям дорог на перекрёстке. Это позволит найти оптимальные правила функционирования светофоров, минимизирующие данные величины.

• 2.    Сокращения и обозначения

В данной работе применяются следующие сокращения и обозначения:

• •    АТС — автотранспортное средство,

• •    с — сигнальный цикл,

• •    сі — время длительности первой фазы,

• •    С2 — время длительности второй фазы,

• •    сз — время длительности третьей фазы,

• •    С4 — время длительности четвертой фазы,

• •    q — поток входящего трафика,

• •    5 — максимальный поток проходящего перекресток трафика.

• 3.    Исследование поведения АТС на перекрёстке с точки зрения теории массового обслуживания

  • 3.1.    Выведение формул задержек АТС с одного направления

Рассмотрим простой поток АТС, прибывающих к светофору с фиксированными временами фаз одного направления. Пусть этот поток - пуассоновский процесс, Һ — длина временного интервала, А — прибытие во время интервала Һ, Е(А(Һ)) = qh.

Пусть Q o — ожидаемая очередь переполнения из предыдущих циклов, то есть очередь АТС на перекрёстке в начале рассматриваемого цикла, Q(t) — очередь АТС во время t.

Введём понятие задержки АТС на светофоре. Задержка АТС равна времени, потраченному АТС на перекрёстке на ожидание. Выразим общую задержку АТС во время одного сигнального цикла как сумму компонент, получающихся при каждой фазе цикла. К примеру, если мы рассмотрим перекрёсток двух дорог со следующими фазами (рис. 1), то

W = Wi + W2 + W3 + W4, где Wi — общая задержка АТС, вызванная первой фазой, W2 — общая задержка АТС, вызванная второй фазой, W3 — общая задержка АТС, вызванная третьей фазой, W4 — общая задержка АТС, вызванная четвертой фазой.

__||__ 1)Х 3)Д

_| г 2)^ 4) ь

Рис. 1. Светофор

Для нашего перекрестка

С 1                  С 1

W 1 =

j Q(t)dt = j

(Q(D) + A(t))dt,

W 2 =

С 1 +С 2 j Q(t)dt, С 1

С 1 +С 2 +С 3

W 3 =

/

Q(t)dt,

С 1 +С 2

W 4 =

С

ˆ

Q(t)dt.

С 1 +С 2 +С 3

Найдём математическое ожидание W i в случае, когда первая фаза - только красный свет. Проинтегрировав (1), получим

E[W i ] = c i Q(D) + j qc ^                              (2)

В статье [1] было введено понятие эффективного числа полос . Воспользовавшись этим аппаратом, мы можем получить, что если k i , к 2 , к з и ^ 4 - соответственные интенсивности потоков, которые могут продолжать движение в каждой фазе, то проходящий поток будет равен не S, а соответственно

Е [S i ] = S • ,

Е [S 2 ] =S • ^,

Е[S 3 ]=S • kl, е [S 4 ] = s • k 4 .

S , максимальная пропускная способность перекрестка с каждой из сторон, - константа для каждой конкретной задачи. Обычно её полагают равной 1800 АТС/час на одну полосу [5].

Определим случайную величину Z i как общую задержку АТС, происходящую во время первой фазы, если ее цикл бесконечен. Z i считается общим временем ожидания во время фазы 1 для процесса очереди Q(t) при составных пуассоновских прибытиях интенсивности q, постоянном времени обслуживания 1/S i при времени Q(t = t o ):

E[Q(t o )]          Е [Q 2 (t o )]

[ 1 ]   2S i (1 - q/S i ) ^{2 +} 2S i (1 - q/S i )'

Так как W i может быть выражено с использованием переменной Z i следующим образом:

E [W i ] = E[Z i | Q(t = с і )] - E [Z i | Q(t = 0)], то, следовательно,

E[Q(c i ) — Q(0)]    E [Q ² (c i )] — E[Q ² (0)]

.

^[ 1 ^]    2S i (1 - q/S i ) ^{2 +}     2S i (1 - q/S i )

Аналогичные размышления можно повторить для 2, 3 и 4 светофорных фаз.

Количество прибывших АТС за цикл равно ^(c); математическое ожидание количества покинувших перекресток АТС на каждой фазе равно S i c i , S 2 C 2 , S 3 C 3 и S 4 C 4 соответственно.

В таком случае если ввести так называемые «избыточные потоки»

P i = q - E[S i ], ^P 2 = q ^{— E [ S} 2 ^], ^P 3 = q ^{- E [ s} 3 ^] , P 4 = q - E [S 4 ].

то

^{E [ Q ( c} i ) ^— ^^{( c} i ) ^{— Q (0) +} ^^(0)] = ^{- S} i ^c i ,

E[Q(c i ) - Q(0)] — - S i c i + E[^(c i ) - A(0)] — - S i c i + qc i — c i P i .

^{E [ Q ( c} i + ^c 2 ) ^— ^^{( c} i + ^c 2 ) ^{— Q ( c} i ) + ^^{( c} i ^)] = ^{— S} 2 ^c 2 ,

E [Q(c i + c 2 ) — Q(c i )] — —S 2 c 2 + E [^(c i + c 2 ) — A(c i )] — —S 2 c 2 + qc 2 — c 2 P 2 .

^{E [ Q ( c} i ^{+ c} 2 ^{+ c} 3 ) ^— ^^{( c} i ^{+ c} 2 ^{+ c} 3 ) ^{— Q ( c} i ^{+ c} 2 ) ⁺ ^^{( c} i ^{+ c} 2 ^)] = ^{- S} 3 ^c 3 ,

^{E [ Q ( c} i ^{+ c} 2 ^{+ c} 3 ) ^{— Q ( c} i ^{+ c} 2 ^)] = ^{- S} 3 ^c 3 ^{+ qc} 3 = ^c 3 ^P 3 .

^{E [ Q ( c)} — ^^{( c)} — ^{Q ( c} i ^{+ c} 2 ^{+ c} 3 ) ⁺ ^^{( c} i ^{+ c} 2 ^{+ c} 3 ^)] = —^S 4 ^c 4 , E [Q(c) — Q(c i + c 2 + c s )j = —S 4 c 4 + qc 4 = c 4 P 4 .

Тогда можно выразить

E[Q(c i )] = Q _o - S i c i + qc i = Q o + c i P i ,

E[Q(c i + c 2 )] = E[Q(c i )] - S 2 c 2 + qc 2 = Q o - S i c i + qc i - S 2 c 2 + qc 2 ,

^{e [ q ( c} 1 ^{+ c} 2 ^)] = ^Q 0 ^{+ c} i ^P i ^{+ c} 2 ^P 2 ,

^{E [ Q ( c} i ^{+ c} 2 ^{+ c} 3 ^)] = ^{E [ Q ( c} i ^{+ c} 2 ^{)] — S} 3 ^c 3 ^{+ qc} 3 ,

^{E [ Q ( c} i ^{+ c} 2 ^{+ c} 3 ^)] = ^Q o ^{+ c} i ^P i ^{+ c} 2 ^P 2 ^{+ c} 3 ^P 3 ,

^{E [ Q ( c )]} = ^Q o ^{+ c} i ^P i ^{+ c} 2 ^P 2 ^{+ c} 3 ^P 3 ^{+ c} 4 ^P 4 .

Таким образом,

^{E [ Q} 2 ^{( c} i + C 2 ) ^{— Q 2 ( c} i ^)] —

= 2E (Q(c i + C 2 ) - Q(c i )) * E(Q(c i )) + E (((Q(c i + C 2 ) - Q(c i )) ² ) —

• ^{—    2( — S} 2 ^c 2 + ^qc 2 ) * ^(Q _O ^— S i ^c i + q^c i ) + S 2 c 2 ^— 2q^c 2> S 2 ^c 2 + ^{E (( A ( c} i + ^c 2 ) ^{— A ( c} i ^{)) 2} ) ^—

• ^{—    2( — S} 2 ^c 2 ^{+ qc} 2^ * ^{( Q} o ^{— S} i ^c i ^{+ qc} i ) ^{+ S} 2 ^c 2 ^{— 2 qc} 2 ^S 2 ^c 2 + ^{E (( A ( c} 2 ^{)) 2 ) —}

• —    2(— S 2 c 2 + qc 2 ) * ( Q o — S i c i + qc i ) + S 2 c ² — 2qc 2 S 2 c 2 + ^p (A(c 2 )) + q^c^ —

• —    2c 2 (q — S 2 ) * ( Q o - S i c i + qc i ) + S 2 c 2 - 2qc 2 S 2 c 2 + qc 2 + q ² c 2 —

• —    2c 2 ^E 2 * ( Q o + c i P i ) + P^G^ + qc 2 .

Аналогично получаем формулы для математических ожиданий из других фаз. Третья фаза:

^{E [ Q} 2 ^{( c} i ^{+ c} 2 ^{+ c} 3 ) ^{— Q} 2 ^{( c} i ^{+ c} 2 ^{)] —}

^{— 2 E ( Q ( c} i ^{+ c} 2 ^{+ c} 3 ) ^{— Q ( c} i ^{+ c} 2 ^{)) E ( Q ( c} i ^{+ c} 2 ^{)) +}

^{+ E ((( Q ( c} i ^{+ c} 2 ^{+ c} 3 ) ^{— Q ( c} i ^{+ c} 2 ^{)) 2 ) —}

• ^{—    2( — S} 3 ^c 3 ^{+ qc} 3 ^{)( Q} o ^{— S} i ^c i ^{+ qc} i ^{— S} 2 ^c 2 ^{+ qc} 2 ^{) +}

+ E((A(c 3 ) — S 3 c 3 ) ² ) —

• ^{—    2( — S} 3 ^c 3 ^{+ qc} 3 ^{)( Q} o ^{— S} i ^c i ^{+ qc} i ^{— S} 2 ^c 2 ^{+ qc} 2 ^{) +}

+ E((A(c 3 )) ² ) — 2S 3 c 3 E [A(c 3 )]+S ² c ² —

• ^{—    2( — S} 3 ^c 3 ^{+ qc} 3 ^{)( Q} o ^{— S} i ^c i ^{+ qc} i ^{— S} 2 ^c 2 ^{+ qc} 2 ^{) +}

+ qc 3 (1 + qc 3 ) — 2S 3 c 3 qc 3 + S 2 c 2 —

• ^{—    2 P} 3 ^ 3 ^{( Q} 0 ^{+ c} i ^P i ^{+ c} 2 ^P 2 ) ^{+ c} 3 ^P 3 ^{+ qc} 3 .

Четвертая фаза:

^{E ( Q} 2 ^{( c ) — Q} 2 ^{( c} i ^{+ c} 2 ^{+ c} 3 )) ^—

• ^{—    2 E ( Q ( c ) — Q ( c} i ^{+ c} 2 ^{+ c} 3 ^{)) E ( Q ( c} i ^{+ c} 2 ^{+ c} 3 )) ^{+ E ((( Q ( c ) — Q ( c} i ^{+ c} 2 ^{+ c} 3 ^{)) 2 ) —}

• ^{—    2( — S} 4 ^c 4 ^{+ qc} 4 ^{)( Q} o ^{— S} i ^c i ^{+ qc} i ^{— S} 2 ^c 2 ^{+ qc} 2 ^{— S} 3 ^c 3 ^{+ qc} 3 ^{) +}

+ qc 4 (1 + qc 4 ) — 2S 4 c 4 qc 4 + S^c ^ —

• —    2 P 4 ^E 4 ( Q o + c i P i + c 2 P 2 + c 3 P 3 ) + € 4 P 4 + qc 4 .

Первая фаза:

E[Q ² (c i ) — Q ² (0)] —

• —    2E (Q(c i ) — Q(0))E(Q(0)) + E (((Q(c i ) — Q(0)) ² ) —

• —    2( — S i c i + qc i )Q o + qc i (1 + qc i ) — 2S i c i qc i + S ² c ² —

• — 2P₁c₁Q o + c 2 P 2 + qci.

Из вышеприведённых уравнений следует

(Et QM -QW]

^[^ ^{i ]}     2S i (1 — q/S i ) ^{2 +}

+ E[Q ² (c i )] — E [Q ² (0)] _—

⁺    2S i (1 — q/S i )

₌ SiE[Q(c i ) — Q(0)]   E [Q ² (c i ) — Q ² (0)] ₌

2(S i — q) ^{2      +}     2(S i — q)

SiciP i    2PiciQ o + c ² P 2 + qci   c i ( — Q o P i — ciPf)

2P 2

-

2P i

2P i

,

E [Ж ] — ciQ o + ^ + c^2.

В случае же, когда у нашего потока дисперсия равна нулю, то есть для равномерного потока:

E [Wi] = C1Q0 + P^ + ciSi^2Pi.(3)

Повторим аналогичные размышления для второй фазы:

E[W2] = ^ + C2(Qo + P1C1)+ C2^2.(4)

Повторим размышления для третьей фазы:

E [W3] = 2 3 + c3(Q0 + Pici + P2C2) + C3/2.

И для четвертой фазы:

PlC 2

E [W4] = 2 + c4(Q0 + P1C1 + P2C2 + P3c3) + c4/2

Для указанного вначале перекрёстка, в котором первая фаза – полностью красная для всех автомобилей, выезжающих снизу, проверим верность полученной формулы. Для равномерного потока у нас есть формула (2), полученная вычислением интеграла. Для данного случая k i = 0, то есть S i = 0, таким образом, из (6) следует

^{E [ W} i ^] = ^C i ^Q 0 +-- 2 1 ^{+ C} i ^S i ^/2P i = ^C i ^Q 0 ⁺ ^2 1 ;

что показывает совпадение результатов при различных методах.

Используя уравнения (3.1), (3.1), (4), (5) и (6), получаем следующее:

^{E [W ]} = ^C i ^Q 0 +-- 2 1 +-- 2" 2 ^{+ c} 2 ^{( Q} 0 ^{+ P} i ^C 1 ⁾⁺

+ 2" ^{3 + c} 3 ^{( Q} 0 ^{+ P} i ^c i ^{+ P} 2 ^C 2 ) +-- 2 4 ^{+ c} 4 ^{( Q} 0 ^{+ P} i ^c i ^{+ P} 2 ^c 2 ^{+ P} 3 ^C 3 ⁾ =

P i C i    P 2 C2 ,    „

= ^cQ 0 +2--1--2--+ ^C 2 ^P 1 ^C 1 ⁺

+— 3 2- ³ + C 3 (P i c i + P 2 C 2 ) +—2- 4 + C 4 (P i c i + P 2 C 2 + P 3 C 3 ) + c/2.

• 3.2.    Поведение АТС на перекрёстке в долгосрочной перспективе

Математическое ожидание изменения длины очереди АТС в конце цикла равно

E[5Q] = c i P i + C 2 P 2 + C 3 P 3 + C 4 P 4 .

Рассчитаем общую задержку со всех направлений за время Т . За первый цикл:

E[W ] — cQ o + c i P i (c i /2 + C 2 + C 3 + C 4 )+

^{+ c} 2 ^P 2 ^{( c} 2 ^{/ 2 + c} 3 ^{+ c} 4 ) ^{+ c} 3 ^P 3 ^{( c} 3 ^{/ 2 + c} 4 ) ^{+ c} 4 ^P 4 ^{( c} 4 ^{/ 2) + c/} 2.

За второй цикл:

E[W] = c(max(Q o + c i P i + C 2 P 2 + C 3 P 3 + C 4 P 4 , 0) + c i ^p i (c i /2 + C 2 + C 3 + C 4 ) + ^{+ c} 2 ^P 2 ^{( c} 2 ^{/ 2 + c} 3 ^{+ c} 4 ) ^{+ c} 3 ^P 3 ^{( c} 3 ^{/ 2 + c} 4 ) ^{+ c} 4 ^P 4 ^{( c} 4 ^{/ 2) + c/} 2.

Таким образом, если мы рассматриваем математическое ожидание суммарной задержки

АТС за время Т (за Т/c светофорных циклов), то

E[W] = c(£X o max(Q o + (c i P i + C 2 P 2 + C 3 P 3 + C 4 P 4^ , 0)+

+ ( c i P i ( c i / 2 + C 2 + C 3 + C 4 ) + C 2 P 2 (C 2 /2 + C 3 + C 4 ) + C 3 P 3 ( c 3 /2 + C 4 ) + C 4 P 4 ( c 4 /2) + c/2) * ^

Перейдём к расчёту суммарной задержки по всем направлениям.

Пусть Ру - избыточный поток для дороги с номером г на фазе j , Q io - начальная очередь АТС на данной дороге. В таком случае суммарная задержка по четырём дорогам равна

Т

^Е [W ^] = c( ^ j=o (max( ^Q io + (c i ^p ii + ^С 2 ^Р і2 + ^С з ^Р із + С 4 ^р і4 )^г, 0) +

^{+ max( Q} 20 + ^{( с} 1 ^р 21 + ^с 2 ^р 22 + ^C 3 ^P 23 + ^С 4 ^Р 24 ^{) г} , ⁰⁾ +

^{+ max( Q} 30 ^{+ ( с} 1 ^Р 31 ^{+ С} 2 ^Р 32 ^{+ С} 3 ^Р 33 ^{+ С} 4 ^Р 34 ^{) г} , ^{0) +}

^{+ max( Q} 40 ^{+ ( с} і ^Р 4і ^{+ С} 2 ^Р 42 ^{+ С} 3 ^Р 43 + ^С 4 ^Р 44 ^{) г} , ^{0)) +}

^{+ ( с} 1 ^{( Р} 11 ^{+ Р} 21 ^{+ Р} 31 ^{+ Р} 41 ^{)( с} 1 /^{2 + с} 2 ^{+ с} 3 ^{+ с} 4 ) ^{+ С} 2 ^{( Р} 12 ^{+ + Р} 22 ^{+ Р} 32 ⁺

^{+ Р} 42 ^{)( с} 2 /^{2 + с} 3 ^{+ с} 4 ) ^{+ С} 3 ^{( Р} 13 ^{+ Р} 23 ^{+ Р} 33 ^{+ Р} 43 ^{)( с} 3 /2 + ^с 4 ^{) +}

^{+ С} 4 ^{( Р} 14 ^{+ Р} 24 ^{+ Р} 34 ^{+ Р} 44 ^{)( с} 4 ^{/ 2)} + ^{2 с )} • ^7 .

Для конкретных перекрёстков величины Р гз можно считать постоянными. Решение этой задачи в общем виде достаточно громоздко и разбивается на множество случаев в зависимости от этих величин.

Число 2с в сумме задержек на каждой фазе показывает, что даже при маленьких потоках задержки при пересечении светофора всё равно будут возникать и связано это с тем, что одновременное движение на перекрёстке по всем направлениям невозможно.

Эта модель достаточно упрощена и не учитывает, к примеру, что АТС начинают своё движение не сразу же после смены светофорной фазы, но для решения задачи оптимизации полученной точности достаточно.

• 3.3.    Применение полученных формул к реальным перекрёсткам

Для конкретного перекрестка двухполосных дорог, рассмотренного и промоделированного в работах [1, 6], рассчитаем общую задержку за светофорный цикл со всех направлений.

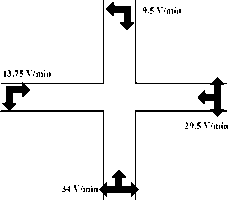
Рис. 2. Перекресток

Phase 4

А- ь ч

Рис. 3. Фазы

Разберемся, какой реальный смысл играют коэффициенты к і , ^ 2 , ^ з , ^ 4 . Пусть у рассмотренного перекрестка поток АТС на нижней дороге распределен следующим образом: X i q АТС имеют цель поворота налево, X _s q - вперёд, Х _т q - направо. Очевидно, что Х [ + X _s + Х _т = 1. Тогда для данного режима светофора к і = Х _т q, к 2 = 0, к з = q, к 4 = (X _r + X _s )q.

Для конкретно нашего перекрестка X / = X _s = Х _т = 1/3, q = 34.

Таким образом,

• •    ^Q 10 = ^Q 20 = ^Q 30 = ^Q 40 = ⁰,

• •    Е [Р_и] = 34 - S * 2 * 1/3 = 34 - 30 * 2 * 1/3 = 14,

• •    Е [Р ₁₂ ] = 34 - 30 * 2 * 1 = - 26,

• •    Е [Р із ] = 34,

• •    Е [Р 14 ] = 34 - 30 * 2 * 2/3 = - 6,

• •    Е [Р 21 ] = 13.75,

• •    Е [Р 22 ] = 13.75,

• •    Е [Р 23 ] = 13.75 - 30 * 2 * 1 = - 46.25,

• •    Е [Р 24 ] = 13.75,

• •    Е [Р 31 ] = 9.5,

• •    Е [Р 32 ] = 9.5,

• •    Е [Р 33 ] = 9.5,

• •    Е [Р ₃₄ ] =9.5 - 30 * 2 * 1 = - 51.5,

• •    Е [Р ₄₁ ] = 29.5 - 30 * 2 * 1 = - 31.5,

• •    Е [Р 42 ] = 29.5 - 30 * 2 * 1/3 = 9.5,

• •    Е[Р ₄₃ ] = 29.5 - 30 * 2 * 2/3 = - 11.5,

• • Е [Р 44 ] = 29.5.

Будем решать задачу минимизации общих задержек в единицу времени: Е(!У)/T.

Таким образом, надо минимизировать функцию

Ғ = (с(ЕІ 0 Сі • max(14c i - 26с 2 + 34с з - 6С 4 , 0) +

+ г • max(13.75c i + 13.75c 2 - 46.25с з + 13.75c 4 , 0)+

+ г • max(9.5c 1 + 9.5с 2 + 9.5с з - 51.5с ₄ , 0) +

+ г • max( - 31.5c 1 + 9.5c 2 - 11.5c ₃ + 29.5c ₄ , 0))+

+ (c i (5.75)(c i /2 + c 2 + c ₃ + c 4 ) + c 2 (6.75)(c 2 /2 + c ₃ + c 4 ) + c ₃(— 14.25)(c ₃ /2 + c 4 ) +

+ c 4 ( - 14.25)(c 4 /2) + 2c) • f )/T =

= (c • 2 ( ^f + 1) ^f ((max(14c i - 26c 2 + 34c 3 - 6c 4 , 0)+

+ max(13.75c i + 13.75c 2 - 46.25c 3 + 13.75c 4 , 0)+

+ max(9.5c 1 + 9.5c 2 + 9.5c 3 - 51.5c ₄ , 0) +

+ max( - 31.5c 1 + 9.5c 2 - 11.5c ₃ + 29.5c ₄ , 0))+

+ (c i (5.75)(c i /2 + c 2 + c 3 + c 4 ) + c 2 (6.75)(c 2 /2 + c 3 + c 4 ) + c 3(— 14.25) + (c 3 /2 + c 4 ) +

+ c4(-14.25)(c4/2) + 2c) • f )/T, что сводится к минимизации следующего выражения:

2 ( ^f + 1)((max(14c i /c - 26c 2 /c + 34c 3 /c - 6c 4 /c, 0)+

+ max(13.75c 1 /c + 13.75c 2 /c - 46.25c 3 /c + 13.75c ₄ /c, 0)+

+ max(9.5c 1 /c + 9.5c 2 /c + 9.5c 3 /c - 51.5c ₄ /c, 0) +

+ max( - 31.5c 1 /c + 9.5c 2 /c - 11.5c ₃ /c + 29.5c ₄ /c, 0)) +

+ c i /c(5.75)(c i /2c + c 2 /c + c 3 /c + c 4 /c) + c 2 /c(6.75)(c 2 /2c + c 3 /c + c 4 /c) +

+ c 3 /c( - 14.25)(c 3 /2c + c 4 /c) + c ₄ /c( - 14.25)(c ₄ /2c).

Так как c 4 = c - c i - c 2 - c ₃ , то это задача минимизации на пирамиде

С і > 0,

С 2 > 0,

С з > 0,

С - С 1 - С 2 - С 3 > 0.

Решение этой задачи зависит от отношения Т/с , количества рассматриваемых циклов, но полученное решение асимптотическое и практически не подвержено колебаниям начиная с Т/с = 50.

Т а б л и ц а 3.1

Зависимость оптимального значения с * /с от количества циклов Т/с

с 1 /с	с 2 /с	С 3 /С	с 4 /с	Т/с
0.208502	0.368045	0.229767	0.193685	40
0.209071	0.367474	0.2292	0.194255	50
0.209071	0.367473	0.229201	0.194255	60
0.209071	0.367474	0.2292	0.194255	70
0.209071	0.367473	0.2292	0.194255	80
0.209071	0.367474	0.2292	0.194255	90
0.209071	0.367474	0.2292	0.194255	100

Таким образом, мы численно показали эргодичность рассматриваемого процесса.

• 3.4.    Поведение АТС в стационарном случае

Рассмотрим решение этой задачи для другого типа перекрёстка, Т-образного, рассмотренного в статье [1].

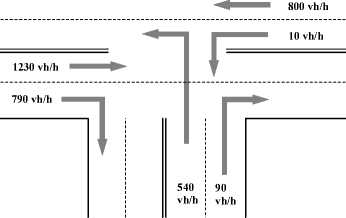
Рис. 4. Перекресток

Phase 1

Phase 3

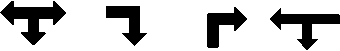
Phase 3

Рис. 5. Перекресток

Для улучшения читаемости дальнейших формул введём следующие сокращения:

Q oi — ^Q io + ^Q 20 + ^Q 30 + ^Q 40 ,

^P ii ^{— P} ii ^{+ P} 21 ^{+ P} 3i ^{+ P} 41 ,

? 2i — P 12 + P 22 + P 32 + P 42 ,                             (8)

• ^P 3i ^{— P} 13 ^{+ P} 23 ^{+ P} 33 ^{+ P} 43 ,

• ^P 4i ^{— P} 14 ^{+ P} 24 ^{+ P} 34 ^{+ P} 44 .

Если мы рассмотрим конкретные фиксированные потоки данного перекрёстка, то P ii — - 25.7, P 2i — - 61.7, Р з і — - 20.7.

Рассмотрим случай перекрёстка со стационарной ненулевой длиной очереди в начале цикла E[Q(0)] — E[Q(c)] и E[Q ² (0)] — E [Q ² (c)]. Это также имеет смысл благодаря эргодичности [3], так как длительность рассматриваемого промежутка времени оптимизации много превышает длительность одной фазы:

^c i ^P ii ^{+ c} 2 ^P 2i ^{+ c} 3 ^P 3i ^{— 0}

В таком случае, так как в стационаре нам достаточно минимизировать задержки на одном светофорном цикле, задача сводится к минимизации следующей функции:

F (c i , С 2 ) — c i (c - c i /2)P ii + C 2 (c

-

^{+ ( c - c} 1 ^{- c} 2 ^{) 2 p} 3i ^{/ 2}.

c i

-

C 2 /2)P 2i +

На треугольнике ci > 0, c2 > 0,

c

-

c i

-

c 2 > 0

при условии ci —

cP 3i

-

^c 2 ^{( P} 2i

-

^p 3i ⁾

^p 3i

-

P ii

.

Тогда максимум функции F одной переменной достигается при

• _—       2cP ii

• ^c 2    P ii + 3P 2i - 4 Р з і .

В таком случае

• _—    З Р і і Р з і + З Р 2 і Р з і - 4 Р з² - 2 Р і і Р 2 і

^{c i}       (P ii + З Р 2 і - 4 Р з і )( Р з і - Р і і ) ^c

• _—          P ii (P ii - P 2i )

• ^{3    ( P} ii ^{+ 3 P} 2i ^{- 4 P} 3i ^{)( P} 3i ^{- P} ii ⁾

В случае, если полученные значения положительны, существует оптимальное решение для стационарного режима работы светофора.

Можно рассчитать ожидаемую задержку в единицу времени на светофоре в данном случае:

^{F — Q} 0i ^{+ c} i ^{/c ( c} i ^{/ 2 + c} 2 ^{+ c} 3 ^{) P} ii ^{+ c} 2 ^{/c ( c} 2 ^{/ 2 + c} 3 ^{) P} 2i ⁺ +c 3 /2cP 3i —

_{= п}    4 Р і і Р 2 і - 5 Р і і Р з і - З Р 2 і Р з і + 4 Р з²

^Q 0 ⁺ 2( Р і і + З Р 2 і - 4 Р з і )( Р і і - Р з і )    ^{ii c.}

Средняя задержка АТС d получается при делении получившегося числа на среднее количество АТС q 1 + q ₂ + 7 3 + q ₄ :

4Р_иР 2 _і - 5Р іг Р зг - ЗР^Р зг + 4Р з2.

d = Ч0 + 2(Рі. +3Р2. - 4Рзг)(Ріг - Рз.)   1гС qi + q2 + дз + q4               "

Аналогичным образом мы можем рассчитать ожидаемые задержки по каждому направлению рассматриваемого перекрёстка.

В случае же, когда стационарная длина очереди в начале цикла равна нулю, выражение (9) сменяется на выражение

С 1 Р іг + С 2 Р 2г + с з Р зг 6 0.                                  (13)

В таком случае, очевидно, надо решить задачу оптимизации функции двух переменных (10) при условиях (13), (11).

Решение этой задачи сильно зависит от избыточных потоков и в общем виде не существует.

Исследуем поведение перекрёстка четырех дорог при стационарной длине очереди:

^С і ^Р іг ^{+ С} 2 ^Р 2г ^{+ С} з ^Р зг ^{+ С} 4 ^Р 4г = ⁰,

С 1 + С 2 + С з + С 4 = С.

Задача сводится к минимизации следующего выражения при вышеуказанных уравнениях связи:

^с 1 ^{( с} 1 / ^{2 + С} 2 ^{+ С} 3 ^{+ С} 4 ^{) Р} іг ^{+ с} 2 ^{( с} 2 ^{/ 2 + С} 3 ^{+ С} 4 ^{) Р} 2г ⁺

^{+ с} з ^{( с} з / ^{2 + С} 4 ^{) Р} зг ^{+ С} 4 ^{/ 2 Р} 4г .

Это достигается при следующих значениях длин фаз:

_с = 2(Р і _г - 2Р 2 _г )(Р 2 _г - Р з_г) Р 4 _{г с}

• ^{- 8 Р}И^Р-ІІ ^{- Р} 1і ^Р 3г ⁺ 8 ^Р 1г ^Р 2г ^Р 3г ^{+ Р} 12і ^Р 4г ^{+ 4 Р} 1г ^Р 2г ^Р 4г ^{+ 4 Р} 2г ^Р 4і ^{- 4 Р} 1г ^Р 3г ^Р 4г ^{- 4 Р} 2г ^Р 3г ^Р 4г ’

_с = 2 Р 1г ( Р 1г + 2 Р 2г - 3 Р з _г ) Р 4г _с

• ^{- 8 Р} 1г ^Р 2 _г ^{- Р} 12 _г ^Р 3г ⁺ 8 ^Р 1г ^Р 2г ^Р 3г ^{+ Р} 12 _г ^Р 4г ^{+ 4 Р} 1г ^Р 2г ^Р 4г ^{+ 4 Р} 2 _г ^Р 4г ^{- 4 Р} 1г ^Р 3г ^Р 4г ^{- 4 Р} 2г ^Р 3г ^Р 4г ’

_с = Р 1г ( Р 1г - 2 Р 2г ) Р 4г _с

• ^{- 8 Р} 1г ^Р 2 _г ^{- Р} 1² _г ^Р 3г ^{+ 8 Р} 1г ^Р 2г ^Р 3г ^{+ Р}^2 _г ^Р 4г ^{+ 4 Р} 1г ^Р 2г ^Р 4г ^{+ 4 Р} 2 _г ^Р 4г ^{- 4 Р} 1г ^Р 3г ^Р 4г ^{- 4 Р} 2г ^Р 3г ^Р 4г ’

= _________________________________ Р 1г (8 Р 22г + Р іг Р зг - 8 Р 2г Р зг) _________________________________

• ^С 4 - 8Р 1г Р^ - Р№ + 8Р 1г Р 2г Р зг + Р^ 4г + 4 Р 1г Р 2г Р 4г + 4Р 22г Р 4г - 4Р_ИР зг Р 4г - 4Р 2г Р зг Р 4г ^С.

• 4.    Заключение

И если при наших потоках в стационарном режиме эти числа получаются положительными, это значит, что у нас есть решение задачи минимизации.

Таким образом, можно также подставить эти значения и найти среднюю задержку АТС на данном перекрёстке.

В настоящей работе рассматривались методы теории массового обслуживания к моделированию транспортных потоков на управляемых перекрёстках. Подробно рассмотрено понятие эффективного числа полос , обосновано и применено при вычислении и минимизации математического ожидания суммарных потерь времени на управляемом перекрёстке. Показано, что методы теории массового обслуживания помогают получить явные формулы задержек, возникающих при пересечении перекрёстка. Предполагаемое развитие темы:

• •    упрощение полученных формул,

• •    обобщение полученных формул на транспортную сеть,

• •    решение задачи транспортной оптимизации на сети управляемых перекрёстков.