Методы ускорения сбора данных в системах однопиксельной визуализации

Однопиксельная визуализация (ОВ) – метод получения изображений с использованием структурированного излучения и детектора без пространственного разрешения [1]. Данный метод может быть реализован в двух вариациях: однопиксельная камера (с англ. single-pixel camera) [2] и фантомная визуализация (с англ. Ghost imaging) [3]. В первом случае излучение, рассеянное объектом, переносится с помощью системы линз на матрицу пространственного модулятора света, после чего отражается или проходит через модулятор и переносится с уменьшением размеров на поверхность интегрирующего детектора. Во втором случае объект наблюдения освещается структурированным излучением, которое рассеивается на объекте, и также с помощью системы линз переносится на детектор без пространственного разрешения. Таким образом, методы реализуют структурированное считывание в случае однопиксельной камеры и структурированное освещение в случае фантомной визуализации. Физическая основа обоих методов заключается в последовательном измерении проекции входного светового поля на заданный набор базисных функций (паттернов). Эта концепция является развитием классических идей оптической обработки информации. В частности, архитектура однопиксельной камеры методологически близка к операциям пространственной фильтрации и оптического разложения по базису [4, 5], где роль согласованного фильтра или базисной функции выполняет паттерн на модуляторе, а однопиксельный детектор регистрирует результат их скалярного произведения с входным полем – корреляционный пик или коэффициент разложения [6,7]. Современное развитие этого направления связано переходом к многоканальным измерениям, где с помощью дифракционных оптических элементов (ДОЭ) разложение по нескольким базисным функциям выполняется одновременно, а для их регистрации используется массив детекторов [8, 9]. Это позволяет рассматривать ОВ не только как альтернативный метод формирования изображений, но и как универсальную платформу для высокоскоростных аналоговых оптических вычислений.

Ключевое отличие фантомной визуализации от однопиксельной камеры – их чувствительность к шумам в системе [10]. Так, устройства на основе однопиксельной камеры более подвержены шумам на пути от объекта до модулятора света, в то время как метод фантомной визуализации больше подвержен шумам на пути от источника модуляции до объекта. Другими словами, для метода однопиксельной камеры важно перенести изображение объекта на плоскость модулятора, а для метода фантомной визуализации – от модулятора излучения до объекта. Однако данное отличие является несущественным, так как в действительности шумы, вызванные, как правило, наличием рассеивающей среды, присутствуют в системе как до, так и после объекта.

Общими условиями для однопиксельной камеры и фантомной визуализации являются необходимость смены паттернов (шаблонов) на поверхности модулятора света, а также последующее сопоставление паттернов со значениями интегральных интенсивностей излучения, измеренных на детекторе без пространственного разрешения. Важным аспектом реализации методов однопиксельной визуализации является формирование структурированного излучения. В связи с этим активно развиваются методы генерации подобных полей, среди которых особое место занимают подходы на основе ДОЭ. Использование ДОЭ является высокоэффективным и гибким решением, позволяющим формировать заранее заданные распределения амплитуды, фазы и поляризации светового поля. Так, с их помощью могут быть получены лазерные пучки Айнса–Гаусса, представляющие собой суперпозицию пучков Эрмита-Гаусса [11], световые поля с управляемой неоднородной эллиптической поляризацией [12], а также пучки со структурированным распределением поляризации для создания микрорельефов [13]. Обзор современных методов генерации структурированного света, включая методы на основе ДОЭ, представлен в работах [14, 15].

От типа паттернов напрямую зависит метод восстановления. Первый вариант – вычисление функции корреляции интенсивностей второго порядка [16]:

G(_x ) _ ^^Bih&y) - ^гВ^^дху)

’ У' N            N N ’ где B[ - интегральная интенсивность излучения после взаимодействия с объектом, It (x, у) - распределение интенсивности паттерна, N - количество измерений. Данный метод обладает малой вычислительной сложностью.

Второй – обратные преобразования, например Фурье [17] или вейвлет [18], которые применяются при использовании паттернов, сформированных из соответствующих базисных функций и характеризуются минимальной вычислительной сложностью. Обобщенно такой метод может быть описан как:

Image (X’ у) = IT{S(U’ v)}, (2) где IT - обратное преобразование, S (и, v) - спектр, получаемый при освещении объекта базисными паттернами. К примеру, для Фурье-паттернов S(u, v) = (D_n - D o ) + j(D_3n/2 - D^, где D_o , D_n/2 , IX , D_3n/2 -интегральная интенсивность излучения при освещении объекта Фурье-паттернами P_F(x, у, 0), P_F(x, у, и/ 2), P_F(x, у, и), Р р (x, у, 3и/2) соответственно.

Третий подход – сжатое зондирование (с англ. compressive sensing) [19,20] – математический метод, позволяющий восстанавливать изображения из существенно меньшего числа измерений, чем предписывает классическая теорема Котельникова (Найквиста) [21]. Этот подход основан на предположении, что изображение является разреженным в некотором базисе (например, в вейвлет базисе), и предполагает решение задачи восстановления через регуляризацию недоопределённой системы линейных уравнений. На практике используются различные методы регуляризации: например, регуляризация по норме L 1 (такие как NESTA [22]) или же алгоритмы минимизации полной вариации (регуляризация по методу полной вариации функции TV, например, TVAL3 [23]:

О,_ \\о\\, где (B_r, -, B t , -, B_M )^т = ГО, (3)

где B - вектор размера М, каждое значение которого соответствует интегральной интенсивности излучения, прошедшего через объект в t-м измерении, о - вектор размерности X X Y, полученный после векторизации изображения О, I - матрица измерений. В данной работе матрица измерений содержит М строк, и каждая строка представляет собой векторизованное пространственное распределение интенсивности соответствующего паттерна в плоскости объекта. Эта система уравнений имеет бесконечное число возможных решений для переменной о. Однако, поскольку естественные изображения сильно сжимаемы, высокая аппроксимация исходного изображения возможна с помощью метода минимизации нормы L 2 , которая вычисляет квадратный корень из суммы квадратов элементов вектора.

Скорость и точность восстановления зависят как от выбранного алгоритма, так и от степени разреженности изображения в выбранном базисе, а также от свойств измерительной матрицы, формируемой набором освещающих паттернов. Обычно сжатое зондирование требует значительных вычислительных ресурсов. Отдельно следует выделить применение нейронных сетей для повышения скорости и качества реконструкции изображения. Они эффективно решают проблему высокой вычислительной сложности алгоритмов сжатого зондирования, что критически важно для систем, работающих в режиме реального времени. Общей чертой всех подходов в этой области является обучение нейронной сети распознавать и улучшать изображение из зашумленного, размытого, восстановленного за малое число измерений фантомного изображения. Одним из ранних примеров являются модели, основанные на полносвязных нейронных сетях, обученных на датасете MNIST для распознавания рукописных цифр, даже при использовании лишь 10% паттернов от полного набора [24]. Однако такие архитектуры склонны к переобучению и не масштабируются на более сложные изображения. В качестве более универсального решения предлагаются сверточные нейронные сети (CNN), специально адаптированные под обработку двумерных структур. В частности, в работе [25] была продемонстрирована возможность восстановления произвольных изображений из 10–25% измерений (100% измерений соответствует числу пикселей в изображении) без потери визуального качества, что подтверждает высокую эффективность сверточных подходов в задаче реконструкции.

Широкий спектр применения в науке и технике стимулирует создание и дальнейшее развитие методов ОВ [26–29]. Так, например, для решения задач дистанционного зондирования, определения местоположения и картографирования территорий с недавнего времени начинают использовать однопиксельные камеры в сочетании с лидарами [30], радарами [31] и камерами с временным стробированием [32]. По сравнению со стандартными методами визуализации ОВ обеспечивает более высокое качество восстановленных изображений в условиях низкой интенсивности излучения [33,34] и повышенной турбулентности среды [35,36]. Методы ОВ также оказываются более эффективными в тех спектральных диапазонах, где ПЗС-камеры дороги или недоступны. Например, в ряде работ была продемонстрирована возможность реализации алгоритма ОВ в ультрафиолетовом [37], коротковолновом инфракрасном [38] и терагерцовом [39] диапазоне частот. Возможность работы в условиях низкой интенсивности излучения и повышенной турбулентности открывает еще одно применение ОВ в микробиологических и медицинских исследованиях [40,41].

Все перечисленные применения требуют высокой скорости восстановления изображения. В связи с этим актуальной задачей является ускорение процесса сбора данных в системах ОВ. Над решением этой задачи работает большое количество научных коллективов по всему миру. Данная работа посвящена обзору разработанных за последние 15 лет подходов к ускорению сбора данных в ОВ.

1.    Основные способы ускорения сбора данных в системах однопиксельной визуализации

Время восстановления изображений в комплексе методов ОВ складывается из двух этапов: сбор данных с экспериментальной установки и обработка этих данных. Наиболее активно развивающимся направлением исследований в этой области физики и техники является уменьшение времени сбора данных, так как для данного этапа открывается множество возможностей для модификации оптической и оптоэлектронной системы, а также внедрения новых технологических решений задачи увеличения скорости работы оптических модуляторов света и интегрирующих детекторов. В то же время скорость обработки экспериментальных данных зависит скорее от математического метода анализа этих данных, а также вычислительных мощностей блока обработки сигналов и вывода изображений для пользователя [42].

Важно отметить, что процесс уменьшения времени сбора данных считается успешным тогда, когда сокращается общее количество измерений при сохранении таких метрик качества как: индекс структурного сходства (SSIM), коэффициент корреляции (CORR), отношение пика к значениям боковых лепестков в функции корреляции между изображениями (PSR), среднеквадратичная ошибка (MSE), отношение сигнал/шум (SNR), пиковое отношение сигнал/шум (PSNR) и т.д. [43]. Для количественной оценки степени уменьшения числа измерений вводится коэффициент сжатия ц, который определяется как ц = К/N, где К- число задействованных паттернов, N - число пикселей в объекте. При этом полным числом измерений считается число измерений, равное числу пикселей в изображении, обусловленное классическими методами визуализации.

Для ускорения сбора данных в системе ОВ существует несколько путей: добавление дополнительных информационных каналов за счет спектрального, поляризационного или временного мультиплексирования, использование сформированных специальным образом паттернов освещения (в том числе их следование в определенном порядке), внедрение методов машинного обучения для уменьшения числа паттернов необходимых для формирования изображений, а также развитие методов адаптивного формирования паттернов в системах с обратной связью. При этом данные способы могут быть скомбинированы друг с другом. Так, например, мультиплексирование паттернов может быть реализовано с оптимизацией последних, так как представляет собой распараллеливание процесса сбора данных, которое реализовывается с любым набором паттернов освещения. При этом именно мультиплексирование паттернов освещения является основой для комбинации этих подходов. Этот факт подтверждают современные исследования, которые направлены на повышение степени мультиплексирования, комбинируя спектральное кодирование с другими степенями свободы светового поля: пространственной, поляризационной и фазовой. Например, использование ДОЭ позволяет эффективно производить мультиплексирование структурированных пучков с различными моментами импульса [44]. В свою очередь, поляризационное мультиплексирование в метаповерхностях позволяет реализовать многофункциональное формирование изображений в компактных системах [45].

Наиболее перспективным трендом является неортогональное мультиплексирование, при котором методы глубокого обучения применяются для демодуляции сложно переплетенных сигналов, значительно повышая пропускную способность канала [46]. Важно отметить, что прогресс в области мультиплексирования движется во многом благодаря его востребованности в смежных областях, таких как визуализация биологических объектов [47] и оптические коммуникации [48]. Этот междисциплинарный опыт напрямую способствует и развитию методов многоканальной ОВ.

• 1.1.    Спектральное, поляризационное и временное мультиплексирование

Применение спектрального мультиплексирования паттернов освещения в системе ОВ позволяет существенно повысить эффективность сбора данных за счёт одновременной обработки информации в различных спектральных каналах. В этом случае необходимо разделить исходное излучение от источника на несколько информационных каналов, каждый из которых характеризуется собственной центральной длиной волны. Такой процесс может быть реализован с помощью нескольких независимых источников излучения с разными длинами волн излучения [49] или путем выделения спектральных компонент широкополосного источника излучения (лампа накаливания, как некогерентный источник, или спектральный суперконтинуум, как когерентный источник) в пространстве [50 – 52]. Далее следует произвести пространственную модуляцию излучения в каждом спектральном канале. Причем необходимым условием для ускорения сбора данных за счет параллельного вычисления изображений является независимость паттернов освещения в каждом информационном канале. При этом подход с несколькими источниками, как правило, требует наличия отдельных систем модуляции излучения для каждого источника, что становится труднореализуемым при увеличении числа спектральных каналов. Второй подход с использованием широкополосного источника требует только один модулятор света, поверхность которого разделяется на сегменты, каждый из которых осуществляет модуляцию излучения с определенной длиной волны. Примером такого подхода может служить работа [52], где спектральное мультиплексирование реализовано с использованием излучения видимой части спектра от спектрального суперконтинуума (рис. 1). Так, спектральное разложение было реализовано с использованием пары дифракционных решеток, установленных по типу оптического компрессора, обычно используемого для компенсации дисперсионного растяжения ультракоротких импульсов. После дифракции широкополосного излучения на первой дифракционной решетке его спектр рассеивался по пространственному углу, в то время как после второй формировался параллельный пучок. Таким образом, каждая спектральная компонента освещает конечную область поверхности модулятора. При взаимодействии излучения с поверхностью жидкокристаллического модулятора света световой пучок дифрагировал таким образом, что излучение каждой спектральной компоненты формировало свое спекл-поле. Далее модулированное излучение проходило по обратному пути через ту же пару дифракционных решеток. Благодаря этому все спектральные компоненты снова были объединены в единый луч, который и освещал объект. Комплексное детектирование модулированного излучения после его взаимодействия с объектом требует повторного разложения на спектр. Это было проведено с использованием спектрометра, построенного по схеме Черни-Тернера [53]. После многократных отражений излучение поступает на решетку, где различные длины волн снова разлагаются под разными углами дифракции, а их интенсивность регистрируется линейкой фотодетекторов.

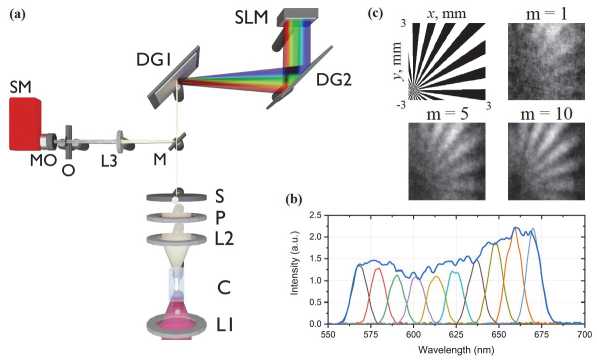
Рис. 1. (а) Экспериментальная установка системы фантомной визуализации со спектральным суперконтинуумом. L1 – 3 – линзы, C – кювета с водой, P – поляризатор, S – щель, DG1,2 – дифракционные решетки, SLM – пространственный модулятор света, M – зеркало, O – объект, MO – микрообъектив, SM – спектрометр; (b) спектр детектируемого сигнала; (с) примеры фантомных изображений, восстановленных с использование одного (m = 1), пяти (m = 5) и десяти (m = 10) спектральных каналов [54]

Такой подход позволяет ускорить процесс сбора данных ввиду того, что в рамках одного измерения система получает значения интегральных интенсивностей для нескольких спектральных каналов. В результате изображение рассчитывается следующим образом:

GKx,у) = Т-^В^х,у) - Т^Т^В^Х^ л (х,У), (4) где В^ - интегральная интенсивность излучения на i-й итерации для длины волны Л, 1^ (х, у) - паттерн освещения на i-й итерации для длины волны Л, N [ - количество измерений, N ^ - количество используемых спектральных диапазонов.

Однако спектральное мультиплексирование в системе ОВ накладывает ограничения на объект наблюдения: в этом подходе необходимо отсутствие особенностей у объекта для каждого спектрального канала визуализации. Другими словами, объект не должен иметь значительно-выраженных линий поглощения на каждой задействованной длине волны излучения. В противном случае данный подход применим не для решения задачи ускорения сбора данных, а для мультиспектрального [55–57] и гиперспектрального анализа [58–60], где необходимо учитывать спектральные характеристики объекта. Также такой способ мультиплексирования накладывает дополнительные требования на систему детектирования ввиду необходимости демультиплексирования на стороне приемника, которое заключается в разделении спектральных компонент в пространстве с целью их независимого детектирования. Таким образом, система ОВ должна включать в себя не один, а несколько однопиксельных детекторов, что приводит к усложнению оптической схемы и, соответственно, увеличению стоимости всей системы.

Существует два решения, позволяющие использовать для спектрального мультиплексирования один широкополосный детектор: разделение сигналов от каждого спектрального канала во времени, то есть реализация время-разрешенного спектрального мультиплексирования [61], или использование ортогональных паттернов в каждом информационном канале [62]. Первый способ подразумевает использование нескольких источников, работающих в импульсном режиме (например, лазерные диоды), с разными длинами волн. Однако в таком случае требуется дополнительная система синхронизации между источниками излучения и однопиксельным детектором, частотная полоса которого должна позволять различить сигналы от каждого источника. Второй способ не требует сложной системы синхронизации, однако накладывает строгие ограничения на выбор паттернов излучения, так как каждому спектральному каналу должен соответствовать свой набор паттернов, который является ортогональным ко всем остальным наборам паттернов в других каналах. Такой метод подходит для двух или трех спектральных каналов, однако теряет свою актуальность при увеличении числа информационных каналов.

Вторая степень свободы, которую можно использовать в оптимизации процесса ОВ, – поляризация излучения. Использование поляризационной степени свободы в системах визуализации с однопиксельным детектором можно разделить на три направления: исследование поляризационных свойств объектов в рамках фантомной поляриметрии [63–65]; устранение искажений, вызванных динамическим поглощением среды за счет внедрения вспомогательного поляризационного канала [66]; поляризационное мультиплексирование для ускорения сбора данных в системе ОВ [67]. Последний подход заключается в распараллеливании процесса восстановления изображений за счет модуляции излучения на отдельных поляризациях света и последующее детектирование двух сигналов от различных поляризационных состояний. Так, например, в работах [68, 69] поляризационное мультиплексирование паттернов освещения реализовано с помощью одного жидкокристаллического пространственного модулятора света, на поверхности которого формировалась специально-заданная фазовая маска. Взаимодействие лазерного излучения с такой маской позволяло сформировать на заданном от модулятора расстоянии два паттерна освещения, разнесенных в плоскости объекта. С помощью системы из зеркал и поляризационного светоделителя реализовывалось соосное распространение паттернов, для одного из которых угол поворота поляризационного эллипса изменялся на 90 градусов с помощью полуволновой пластины (рис. 2). Дальнейшее распространение двух паттернов с ортогональными поляризациями через объект и разделение излучения в системе детектирования на два однопиксельных детектора позволило распараллелить процесс сбора данных. Тем самым было продемонстрировано увеличение скорости сбора данных в системе ОВ в 2 раза за счет мультиплексирования по поляризации паттернов освещения.

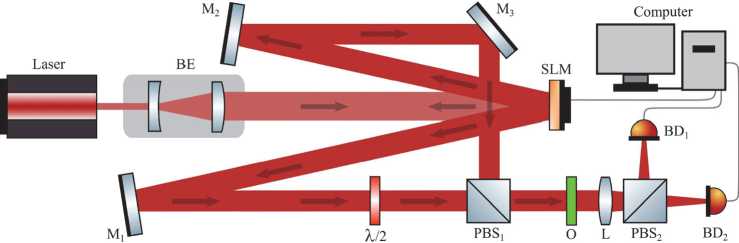
Рис. 2. Экспериментальная установка системы ОВ с двумя поляризационными каналами. BE – расширитель пучка, SLM – пространственный модулятор света, M i-з - зеркала, Л/2 - полуволновая пластина, PBS 1,2 - поляризационные светоделители, O – объект, L – линза, BD 1,2 – однопиксельные детекторы [69]

При этом для поляризационного подхода можно выделить схожие со спектральным методом проблемы, такие как дополнительные ограничения на объект наблюдения и необходимость использования нескольких однопиксельных детекторов. Однако в приложениях дистанционного зондирования и составления карт местностей объекты наблюдения крайне редко обладают свойством оптической активности, что нельзя сказать про спектральные особенности, учет которых значительно ограничивает применение спектрального мультиплексирования как метода ускорения сбора данных в системе ОВ. В соответствии с этим поляризационное мультиплексирование как метод уменьшения времени сбора данных в системе ОВ считается более предпочтительным методом для широкого спектра применений.

Временное мультиплексирование паттернов освещения позволяет распараллелить процесс сбора данных при наличии нескольких источников излучения. В таком случае для нескольких информационных каналов используется один и тот же набор паттернов освещения. Дальнейшее временное разделение сигналов на детекторе позволяет извлечь информацию из каналов, которые могут отличаться друг от друга по длине волны, пространству или поляризации. Классические методы ОВ характеризуются необходимостью последовательного сканирования объекта различными паттернами, что ограничивает скорость получения изображения. Современные исследования демонстрируют, что применение методов временного мультиплексирования позволяет преодолеть это ограничение и реализовать высокоскоростную регистрацию динамических процессов. В исследовании [70] предложена методика, основанная на попеременном использовании двух типов паттернов: геометрических моментов для определения координат объекта и паттернов Адамара для реконструкции изображения. Данный подход обеспечивает параллельное получение информации о пространственном положении объекта и его пространственных характеристиках. Достигнутая частота определения координат положения объекта составляет 5,55 кГц, что существенно превышает показатели стандартных систем ОВ. Метод не требует априорных данных о траектории движения объекта и осуществляет коррекцию проекционных паттернов в режиме реального времени. Альтернативный подход представлен в работе [71], где реализовано комбинирование временного и спектрального разделения сигналов. Система осуществляет одновременную проекцию трех цветовых каналов RGB, каждый из которых модулируется на отдельной частоте. Последующее частотное разделение методом Фурье-анализа позволяет восстановить цветовую информацию без необходимости последовательного сканирования. Данная методика демонстрирует устойчивость к внешним помехам, включая вариации внешней освещенности, что важно для практических применений в неконтролируемых условиях. Наиболее высокую скорость регистрации демонстрирует система из работы [72], использующая частотно-временное мультиплексирование. Применение частотных гребенок с временным сдвигом сканирования позволяет достичь частоты смены паттернов до 32 000 кадров/ с. Такая производительность особенно востребована при исследовании быстропротекающих процессов, включая гидродинамические явления и клеточную динамику в потоке. Система обеспечивает высокое отношение сигнал-шум за счет алгоритмов комбинирования данных от различных частотных каналов.

Табл. 1. Сравнение методов ускорения сбора данных в системах ОВ с помощью мультиплексирования паттернов освещения

Метод мультиплексирования	Количество информационных каналов	Особенности и ограничения
Спектральное	от 2 до 25	Объекты без спектральных особенностей в выделенном диапазоне частот. Линейка детекторов.
Поляризационное	2	Объекты без дихроизма
Временное	от 2 до 5	Детектор с временным стробированием

• 1.2.    Оптимизация паттернов освещения

Оптимизация паттернов в ОВ является одним из ключевых подходов, направленных на снижение времени сбора данных при сохранении заданного качества восстанавливаемого изображения. Поскольку в таких системах каждый паттерн соответствует одному измерению, уменьшение их числа напрямую влияет на скорость формирования изображения. Таким образом, задача оптимизации сводится к поиску информативных, эффективно кодирующих световых шаблонов, обеспечивающих высокую точность реконструкции при минимальном объеме данных.

На практике часто рассматриваются следующие классы паттернов:

• 1.    Случайные паттерны, модификация которых состоит либо в изменении их частотной характеристики так, чтобы она соответствовала различным видам шума [73], либо в расширении её спектра пространственных частот [74].

• 2.    Ортогональные, например, основанные на преобразованиях Уолша–Адамара [75] или Фурье [76].

• 3.    Паттерны, сгенерированные с помощью методов машинного обучения [77].

Выбор паттернов оказывает влияние не только на качество итогового изображения, но и на вычислительную сложность используемых алгоритмов восстановления, что делает данный этап критически важным при проектировании и практическом применении систем ОВ.

Немодифицированными паттернами считаются случайные паттерны с белым шумом – шумом с равномерным спектром мощности. Это могут быть как дискретные (например, Бернуллиевы), так и непрерывные (например, Гауссовы) распределения [73]. Они отличаются простотой генерации, однако не являются взаимно ортогональными. Их коррелированность приводит к накоплению ошибки при восстановлении изображения методом ОВ, что в свою очередь приводит к неидеальному качеству даже при передискретизации – числу измерений более N² для получения изображения N X N [78]. Альтернативой белому шуму является розовый -шум с доминирующими низкими частотами. В отличие от белого шума, где соседние пиксели некоррелированы, розовый шум обладает значимой положительной корреляцией между соседними пикселями, что и обеспечивает его устойчивость к фоновым искажениям полезного сигнала. Розовый шум позволяет достичь приемлемого качества изображения уже при 15 % от полного числа измерений, тогда как для белого шума требуется полный набор данных для сопоставимого результата. Более того, при малом числе измерений розовый шум демонстрирует снижение среднеквадратичной ошибки (MSE) в 5–8 раз по сравнению с белым шумом [79].

Модификацией случайных паттернов является их ортогонализация, например, методом Грамма-Шмидта [80]. Такой подход преобразует исходные коррелированные векторы в ортогональную систему, что обеспечивает статистическую независимость измерений и снижает избыточность данных. В работе [73] показано, что ортогональные паттерны позволяют достичь PSR на ~5 дБ выше по сравнению с гауссовыми при том же коэффициенте сжатия ) = 0,9, а также улучшают SNR с ~15 дБ до ~20 дБ. Кроме того, они демонстрируют устойчивую работу при значительно меньших значениях () > 0,3), тогда как случайные паттерны с белым шумом требуют ) > 0,7 для приемлемого качества реконструкции. Таким образом, несмотря на дополнительные вычислительные затраты, связанные с ортогонализацией, данный подход обеспечивает существенное повышение эффективности измерений и качества восстановленного изображения.

При формировании паттернов одним из ключевых контролируемых параметров, определяющих качество изображения, является их набор пространственных частот. Это подтверждается в работе [81], авторы которой демонстрируют, что с увеличением размера спекла PSNR сначала растет, достигает максимума, а потом падает. Для обеспечения гибкости в выборе пространственных частот и преодоления ограничений традиционных паттернов с фиксированной сеткой был предложен инновационный метод генерации паттернов со сдвигом, в котором спеклы распределяются случайным образом с возможностью перекрытия. Такой подход демонстрирует превосходство в 2–3 дБ по PSNR для крупных спеклов (например, 20–21 дБ против 18 дБ при 24 X 24 пикселях), а также лучше сохраняет детализацию за счёт плавных переходов между областями.

Ещё один пример применения пространственно-вариативных паттернов, объединяющих компоненты с различными пространственными частотами в единой структуре, являются «фовеальные» паттерны. Они имитируют структуру сетчатки, где центральная область (фовеа) имеет высокое разрешение, а периферийная – низкое [82]. Данный подход обеспечивает повышение качества реконструкции: в фовеальной области достигается увеличение PSNR на 6–8 дБ по сравнению с равномерным разрешением. При этом снижается вычислительная нагрузка, число измерений сокращается. Интеграция с методами машинного обучения позволяет адаптивно корректировать зону фовеации в реальном времени (см. Раздел 1.3).

Случайные паттерны широко применяются в технологиях сжатого зондирования. Этот подход основывается на принципе разреженности сигналов в определённых базисах и даёт возможность восстановления изображений даже при числе измерений 10–30% от общего числа пикселей, что существенно снижает требования к объему данных [83]. Однако эффективность метода сильно зависит от выбора базиса, в котором сигнал является разреженным. Традиционные базисы, такие как вейвлеты Хаара или Фурье-базис, имеют ограниченную применимость: вейвлеты хорошо подходят для сцен с резкими границами, а Фурье-преобразование – для гладких изображений. В отличие от них случайные паттерны обладают универсальностью, поскольку не зависят от конкретной структуры сигнала. Тем не менее, их использование сопряжено с необходимостью применения вычислительно сложных алгоритмов восстановления, требующих значительных ресурсов.

Несмотря на преимущества использования ортогональных паттернов для сжатого зондирования, восстановление изображения с их использованием производится также с помощью обратных преобразований, что значительно снижает вычислительную нагрузку. Каждый коэффициент преобразования соответствует результату измерения проекции объекта на соответствующую маску. При этом также остается возможность использовать функцию вычисления корреляции второго порядка.

Альтернативными методами ускорения восстановления изображений являются методы обратного вейвлет-преобразования. Для восстановления методом обратного вейвлет-преобразования зачастую используются вейвлеты Хаара. Ключевым преимуществом вейвлет-преобразования является возможность адаптивного измерения, при котором регистрируются только наиболее значимые коэффициенты, а малозначимые отбрасываются [20]. Такой подход позволяет сократить количество измерений в 15–20 раз по сравнению с полным числом измерений, значительно ускоряя процесс сбора данных. Адаптивное измерение также комбинируется с бичастотным освещением и позволяет использовать 5% данных [84].

Следующим базисным подходом является метод Фурье однопиксельного изображения (FSI – Fourier Single-Pixel Imaging), который использует градационные паттерны Фурье. Для получения фурье- коэффициента, соответствующего одной частоте, необходимо провести 3 или 4 измерения [17]. При этом изображение восстанавливается даже при неполном спектре (например, 10 – 25 % измерений), так как низкие частоты несут основную информацию, что позволяет проводить меньше количество измерений, чем число пикселей изображения. Альтернативно существует метод синусоидального фантомного изображения (SGI – Sinusoidal Ghost Imaging) [85], в котором используются ортогональные синусоидальные паттерны, основанные на двумерном ряде Фурье. Выбор диапазона частот позволяет контролировать детализацию изображения. Это в свою очередь позволяет добиться высокого качества изображения (SNR ~33 дБ) при значительно меньшем числе измерений: для изображения 200 × 200 пикселей требуется всего 2812 паттернов против 40000 – 100000 в вычислительной фантомной визуализации со случайными паттернами. Авторы оптимизируют процесс, используя 30 частот, что обеспечивает быстрое восстановление без потери детализации изображений.

Так как Фурье-паттерны представляют собой не бинарные изображения, это создаёт трудности при использовании цифровых микрозеркальных устройств (ЦМУ), так как те работают по бинарному принципу – у каждого микрозеркала возможно только 2 положения. Несмотря на решения, позволяющие бинаризовать паттерн [86], зачастую используют другой подход – восстановление изображения с помощью обратного преобразования Адамара (HSI – Hadamard Single-Pixel Imaging). Этот метод более устойчив к шуму и идеально подходит для систем с ЦМУ. Паттерны формируются из строк матрицы Адамара. Так как её значения это 1 и –1, то из одной строки формируют два паттерна - положительный Р₊, в котором -1 заменены на 0, и отрицательный - Р _ = 1 — Р₊. В классическом подходе для получения одного коэффициента для преобразования Адамара требуется 2 измерения – «положительными» и «отрицательными» паттернами. Модификацией является использование лишь одного измерения на коэффициент с использованием только «положительных» паттернов Адамара [87]. Так как в таком случае число измерений оказывается равно числу пикселей изображения, то для его уменьшения используются различные порядки паттернов. Например, освещение в порядке zig-zag [88], позволяет достичь качества восстановления, близкого к исходному изображению даже при 20 % выборке. Порядок cake-cutting [89] демонстрирует успешное восстановление при коэффициенте сжатия ц = 0,2. Для сцен с однородным фоном освещение в порядке «Russian Dolls» [75] показывает отличное качество восстановления даже при малом количестве паттернов (например, 6%), тогда как для сложных сцен может потребоваться больше паттернов (например, 25–50 %).

Базисные методы удачно комбинируются между собой. Например, в работе [90] для улучшения качества восстановления изображений, устойчивости к шуму и эффективности при низких частотах дискретизации паттерны создаются путем преобразования строк матрицы Адамара в соответствии с двумерным вейвлет-базисом Хаара. Метод демонстрирует высокое качество восстановления даже при 15 % от общего числа измерений. Комбинация вейвлетов (для анализа) и случайных паттернов (для измерений) [91] также позволяет сократить необходимое число измерений и ускорить восстановление. Вначале изображение сканируется с помощью крупных случайных паттернов, затем применяется вейвлет-преобразование, чтобы найти области с важными деталями. В выявленных областях генерируются новые случайные паттерны меньшего размера. Процесс повторяется, пока не будет достигнуто нужное разрешение. Такой подход позволяет использовать для изображения 256 × 256 ~25–40 % от общего числа пикселей. Для 512 × 512 – ~40 – 60 %, но точные цифры зависят от сложности сцены и выбранных порогов. При этом возможна генерация паттернов путём свёртки уже известных. Так в работе [92] паттерны создаются путем свертки вейвлетов Морле с белым гауссовым шумом и сочетают случайные и детерминированные свойства. При 4%-сжатии PSNR достигает 25 дБ (против 14 дБ у Уолша-Адамара и 22 дБ у нойзлетов, где нойзлеты – это специальные дискретные ортогональные функции, разработанные для компрессированного зондирования [93].

Отдельно следует выделить подходы с использованием глубокого обучения, которые позволяют подобрать оптимальные паттерны для формирования изображений, а также снизить требования к числу паттернов и повысить качество изображения. Как правило глубокое обучение, в контексте ОВ, применяется в конкретных практических приложениях. Например, в применении к волоконным эндоскопам в схеме с однопиксельным детектированием. В таких системах паттерны являются комбинацией собственных мод многомодового волокна и задаются изгибом волокна, или модуляцией излучения на выходе. В работе [94] для улучшения разрешения формируемых изображений используется U-net подобная необученная нейронная сеть. Для тестового объекта, масштабы которого порядка 16 мкм, подход авторов позволяет различить структуру мишени при частоте дискретизации 0,6%. Напротив, изображение, полученное традиционным фантомным методом, полностью зашумлено и не содержит полезной информации.

Глубокое обучение используется также и в фантомной поляриметрии. В работе [95] авторы продемонстрировали возможность уменьшения числа использованных паттернов для определения поляризационных свойств двумерных дихроичных объектов. Авторы сравнили аналитический подход к оценке параметров анизотропии в схеме фантомной поляриметрии и подход на основе глубокого обучения. На модельных данных, рассчитанных для схемы, изображенной на рис. 3, показано, что суммарное число паттернов может быть уменьшено в 27 раз, при сохранении той же точности определения параметров анизотропии.

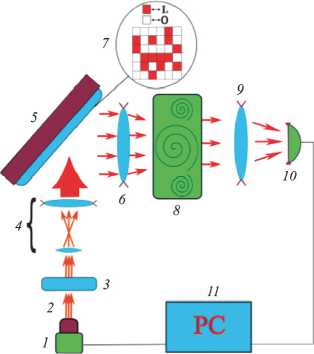
Рис. 3. Схема моделируемой установки [95]. 1 – He-Ne лазер, 2 – лазерное излучение, 3 – полуволновая пластина, 4 – расширитель пучка, 5 – амплитудный пространственный модулятор, 6 – объектная линза, 7 – пример пространственного распределения интенсивности вблизи пространственного модулятора, 8 – объект, 9 – собирающая линза, 10 – однопиксельный детектор, 11 – компьютер

Более общий результат представлен в работе [77]. Авторы использовали глубокий сверточный автоэнкодер обучавшийся на датасете STL-10 и формировали оптимизированный базис, который лучше всего подходит для восстановления изображений из малого числа измерений. Этот подход дает сети возможность выучить универсальные паттерны для разных объектов. Его сравнивали с оптимизированным порядком паттернов Адамара. Для разрешения 128×128 пикселей: для числа измерений = 333 (98 % сжатия): PSNR: 22,7 дБ (машинное обучение) и 20,8 дБ (оптимизированный порядок паттернов Адамара).

Отдельно стоит выделить применение квантовых нейронных сетей в задаче ОВ. В работе [96] сравнивается использование классических и квантовых нейронных сетей для задач классификации и восстановления в схеме ОВ. Отметим, что в отличие от большинства работ здесь в нейронную сеть поступает сигнал напрямую с суммирующего детектора. При частоте дискретизации 0,06 % задача классификации была решена с точностью 96 % и 95 % для классического и квантового подхода, соответственно. При этом квантовые нейронные сети, при достаточном уровне развития технологии, могут ускорить процесс извлечения информации в разы. Похожее исследование проведено в работе [97]. Авторы предлагают алгоритм квантовой нейронной компрессионной фантомной визуализации для уменьшения требований к количеству измерений при формировании высококачественного фантомного изображения. По сравнению с традиционными методами фантомной визуализации с поддержкой машинного обучения, алгоритм авторов демонстрирует более высокое качество реконструкции изображений. Данный алгоритм использует физическую модель в оптимизации архитектуры квантовой нейронной сети. При этом показана устойчивость к экспериментальному шуму, так эффективно восстанавливается изображения даже в условиях SNR около 12 ∼ 20 дБ.

• 1.3.    Адаптивная однопиксельная визуализация

  Третье направление включает целое семейство методов, главной особенностью которых является наличие обратной связи от детектора. Благодаря этому достигается возможность непрерывной подстройки формируемых паттернов и оптимизация процесса восстановления изображения. Например, при адаптивном подходе детектирования сцена изначально может сканироваться в выбранном базисе. Можно получить изображение с помощью шаблонов Фурье, дискретного косинусного преобразования, вейвлет-шаблонов и т.д. Адаптивность касается элементов выбранного базиса, которые должны детектироваться на основе выбранного метода обратной связи для прогнозирования шаблонов. Элементы базиса, которые не были считаны, отбрасываются и принимают значение 0. Главное преимущество заключается в том, что восстановление изображения осуществляется напрямую с использованием обратного преобразования выбранного базиса. Это позволяет избежать вычислительных затрат на минимизацию нормы L 1 . Вычислительные затраты переносятся с восстановления на прогнозирование. В описанной выше комбинации случайных паттернов и вейвлетов [20, 91, 98] алгоритм измерения и восстановления изображения основывается на итерационной максимизации вейвлет-коэффициентов относительно предопределенного порогового значения, учитывающегося при формировании отправляемых на объект сканирующих паттернов на каждом этапе вейвлет-преобразования (от корней до листьев вейвлет-дерева, соответствующих среднему значению по необработанному изображению и горизонтальным, вертикальным и диагональным границам объектов в наблюдаемой сцене). Такой адаптивный метод сжатия на основе вейвлет-деревьев в работе [99] позволил восстановить изображения 512 × 512 пикселей с помощью только 55% измерений из 5122, установленных критерием Найквиста, за 50,06 секунд. Описанный подход не требует

априорного знания объекта и собирает информацию только о соответствующих частях сцены, содержащих объекты интереса, адаптивным способом (основной критерий – наблюдение ненулевых границ объектов в вейвлет-преобразованных изображениях). Он основан на считывании сцены с помощью небольшого набора масок, которые адаптивно изменяют размер, когда часть сцены необходимо записать с более высоким разрешением. Изображение в итоге восстанавливается с помощью быстрых вейвлет-преобразований. В такой конфигурации удается сохранить малое количество требуемых для восстановления изображения паттернов, и в то же время минимизировать время на постобработку – фактор, который играет значительную роль в скорости работы методов ОВ на сжатом зондировании. Кроме того, из-за природы адаптивной ОВ, увеличение размера сцены само по себе не подразумевает увеличение требований к оперативной памяти вычислительного оборудования, что позволяет восстанавливать изображения в несколько мегапикселей на стандартном лабораторном компьютере: необходимо сохранить только небольшой набор масок низкого разрешения и вектор измерений. Существует более комплексное развитие описанного базиса адаптивного метода ОВ, например, в работе [100], где используется нелинейная аппроксимация вейвлет-преобразования с использованием метода интерполяции для прогнозирования значимых вейвлет-коэффициентов, которые необходимо получить экспериментально, в то время как другие коэффициенты можно отбросить.

Адаптивность метода ОВ может выражаться в подстройке к динамичности сцены, наблюдаемой в реальном времени. Так, в работе [101] описывается метод ОВ в реальном времени, который может адаптивно перестраивать алгоритм восстановления изображения в соответствии с изменениями в наблюдаемой сцене. Идея основывается на Фурье ОВ (FSI) [86], которая позволяет получать изображения и фиксировать изменения в наблюдаемой сцене [102] в реальном времени, поскольку она использует обратное преобразование Фурье при восстановлении изображения: при изменении сцены изменяются все Фурье-коэффициенты, а значит достаточно наблюдать за ограниченным количеством коэффициентов. В данном случае происходит быстрое переключение между алгоритмами, настроенными на максимизацию либо параметра временное разрешение (TR), либо параметров пространственное разрешение (SR) и соотношение сигнал/шум (SNR), адаптивно подстраиваясь под характер наблюдаемой сцены.

Как уже было сказано, возможности сбора данных вычислительной однопиксельной системы визуализации можно расширить, имитируя адаптивное фовеальное зрение, широко распространенное в животном мире. В работе [103] описывается методика, по которой фовеальная область с высоким разрешением отслеживает движение в пределах сцены, но в отличие от простого приближения каждый кадр представляет собой новую пространственную информацию со всего поля зрения. Подобный алгоритм позволяет детектировать детали быстро меняющихся особенностей сцены, одновременно накапливая детали медленно развивающихся областей в течение нескольких последовательных кадров. Эта архитектура обеспечивает видеопотоки, в которых как разрешение, так и время экспозиции пространственно изменяются и динамически адаптируются в ответ на эволюцию сцены.

Стоит отметить, что для адаптивного восстановления изображения при ОВ не обязательно использовать подходы, использующие обратные преобразования. Например, в работе [104] область интереса определялась из прямого изображения. На каждом шаге алгоритма с помощью случайных паттернов восстанавливается изображение сцены классическим методом, после чего оно сравнивается с изображением, полученным на предыдущем шаге. Чтобы определить, достаточно ли восстановлена отдельная часть полученного изображения или нет, вычисляется MSE между текущим изображением и предыдущим в пределах рассматриваемой части. Если MSE достаточно мала, то текущее изображение рассматриваемой части принимается как готовое. Такой подход эффективен и основывается на наблюдении, что MSE между полученным фантомным изображением и восстанавливаемой сценой достигает своего минимума, когда средний размер спеклов близок к размеру элемента объекта, восстановленного из заданного числа спекл-шаблонов. Исходя из определенной таким образом области интереса, которая требует дальнейшего восстановления, сканирующий спекл-паттерн перестраивается для эффективного восстановления изображения именно в этой области. Такой адаптивный подход также значительно ускоряет ОВ по сравнению с классическими методами.

Динамическая адаптация к наблюдаемой сцене может быть реализована с использованием методов машинного обучения. Это в том числе позволяет увеличить скорость восстановления за счет параллелизации процесса обучения для создания паттернов и процесса восстановления изображений. Например, в работе [105] описывается новый алгоритм минимизации TV, который использует адаптивное глубокое обучение со словарем при ОВ. По сравнению с ОВ, основанными на методах глубокого обучения [106], предлагаемый алгоритм использует сканирующую матрицу и измеренную общую интенсивность света в качестве входных данных для получения восстановленных изображений, вместо использования самих восстановленных изображений в качестве вводных данных для обучения нейронной сети. Таким образом, предлагаемый алгоритм обеспечивает оптимизацию паттернов непосредственно во время процесса восстановления, а не во время постобработки восстановленного изображения.

В рамках подходов с использованием методов машинного обучения также выделяется адаптивное использование описанных ранее фовеальных паттернов [74, 107]. Сначала восстанавливается изображение с низким разрешением для обнаружения объектов. По таким изображениям нейронная сеть определяет области интереса, после чего на объект посылаются уже фовеальные паттерны с высокими пространственными частотами в области обнаружения объекта. При этом за счет обратной связи метод адаптируется к объектам произвольного размера и положения и позволяет перемещать положение высокочастотной области при формировании паттерна. Такой подход обеспечивает увеличение PSNR в области интереса и сокращает эффективное число пикселей в паттерне, тем самым уменьшая время реконструкции.

Перспективным направлением для создания новых методов ускорения сбора данных в системах ОВ, особенно в контексте адаптивных схем, является использование оптических и фотонных нейронных сетей [108, 109]. В отличие от стандартных алгоритмов, работающих на электронных процессорах, оптические нейронные сети позволяют осуществлять вычисления со скоростью света и с крайне низким энергопотреблением, выполняя операции в аналоговой форме непосредственно в оптической среде. Это открывает возможность для создания полностью оптических систем ОВ с замкнутым контуром обратной связи, где этапы формирования адаптивных паттернов и восстановления изображения будут выполняться практически мгновенно. Уже продемонстрированы успешные применения оптических нейронных сетей для таких смежных задач, как классификация изображений на различных длинах волн [110], создание перестраиваемых спектральных фильтров [111] и даже классификация объектов непосредственно по данным однопиксельного детектора [112]. Таким образом, объединение методов машинного обучения и фотонных технологий создаёт основу для разработки нового поколения высокоскоростных и энергоэффективных адаптивных систем ОВ.

Заключение

Ускорение процесса сбора данных в системах однопиксельной визуализации представляет собой многогранную задачу, охватывающую широкий спектр подходов. Ключевые стратегии включают как усовершенствование экспериментальной схемы – в частности, за счёт применения мультиплексирования, – так и разработку алгоритмов формирования шаблонов модуляции излучения. Кроме того, всё более важную роль играют методы, использующие обратную связь от детектора, что открывает возможности для адаптивного управления процессом измерения и повышения эффективности восстановления изображений.

Выбор конкретной стратегии ускорения сбора данных в однопиксельной визуализации во многом определяется свойствами визуализируемых объектов и доступными измерительными ресурсами. Так, для объектов с предсказуемой структурой целесообразно использование априорно обученных паттернов. В то же время при визуализации сложных или неизвестных объектов, особенно в условиях низкого отношения сигнал/шум, предпочтение может отдаваться методам с мультиплексированием.

При этом важным направлением развития становится комбинация существующих подходов. Их объединение позволит более эффективно использовать измерительные ресурсы и открывает путь к созданию высокопроизводительных систем однопиксельной визуализации, применимых в реальном времени.

Разделы «Введение», «Спектральное, поляризационное и временное мультиплексирование» и «Оптимизация паттернов освещения» подготовлены авторами В.С. Шумигай, А.К. Лаппо-Данилевская, А.О. Исмагилов, Е.Н. Опарин и А.Н. Цыпкин при поддержке Государственного задания № FSER-2025-0007. Раздел «Адаптивная однопиксельная визуализация» подготовлен автором А.С. Синько в рамках государственного задания НИЦ «Курчатовский институт». Раздел «Заключение» подготовлен автором Д.П. Агапов.