Метрическое пространство прецедентов

Опыт эксплуатации различных сложных технических систем часто описывается в форме множества, прецедентов - описаний отдельных фактов нештатных ситуаций (НС) и действий по их устранению в текстовой форме. Основным отличием программных систем (ПС) от сложных технических систем является принципиальное наличие оператора (эксперта. или пользователя), который корректирует НС в работе ПС. В технических системах большая часть внешних воздействий, могущих привести к НС, компенсируется автоматическими системами управления, основанными на. принципе обратной связи. По аналогии с техническими системами процесс коррекции НС рассматривается как контур отрицательной обратной связи, в котором определенное возмущающее воздействие, приводящее к возникновению НС, компенсируется дополнительным, корректирующим воздействием, которое осуществляет эксперт на. основании сообщений системы о НС и собственных гипотез о её причинах (см. рис. 1).

Суть автоматизации процесса, принятия решения заключается в накоплении опыта, по идентификации и коррекции НС, поиске по запросу пользователя или эксперта, наиболее подходящей гипотезы и соответствующих ей способов коррекции. Опыт экспертов накапливается в виде прецедентов, то есть структурированных описаний конкретных процессов возникновения, идентификации и коррекции НС.

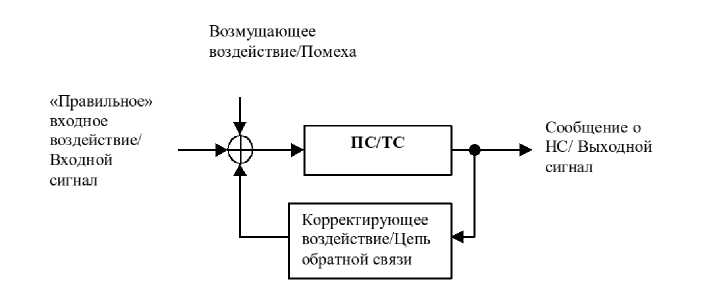
Рис. 1. Сравнение моделей коррекции программных и технических систем

Выделим следующие основные элементы процесса коррекции НС:

• 1)    S, собственно программная система.

• 2)    V, проявления НС.

• 3)    R, гипотезы о причине возникновения НС.

• 4)    Q, действия пользователя по коррекции НС.

2.    Формальное описание множества прецедентов

Построение системы анализа накопленного опыта в рамках модели коррекции нештатной ситуации (МКНС) может быть основано на концепции сходства прецедентов и образовании классов близости. В соответствии с этой концепцией все прецеденты разбиваются на кластеры на основании введенной степени сходства, или близости, между прецедентами. В этой статье попытаемся описать построение метрического пространства прецедентов с определенной в нем метрикой, отражающей степень сходства прецедентов между собой. При определении метрики используем опыт построения метрик в теории алгебраического кодирования, в частности метрики Хэмминга и различные комбинаторные нехэммингов-ские метрики. Далее, пользуясь метрическими свойствами пространства, можно строить процедуры контроля корректности множества прецедентов и алгоритмы поиска в нем.

В соответствии с выделенными выше качественными компонентами процесса коррекции НС введем системологические переменные с конечными множествами значений. Совокупность четырех конкретных переменных с множествами их значений образует I, представляющий набор МНКС.

• ¹    = ^((s,S), (v^,V), ^(r,R), ⁽q, ^Q)), (1)

где s, v,r,q - переменные МКНС, V = {щ} ; R = {rj} ; Q = {q^} ; S = {sj} - множества их значений, причем V - множество сообщений о НС, Q - множество гипотез о причинах НС, R - множество корректирующих действий по устранению НС, S - множество элементов системы.

Совокупность множеств S, V, R, Q образует информационную базу процесса коррекции НС, А = (S, V, R, Q). Формальная модель предполагает, что существует четкий канал наблюдения, то есть пользователь может однозначно соотнести наблюдаемую НС с элементами из множества значений переменных. С учетом введенных обозначений качественная модель идентификации и коррекции НС преобразуется в следующую схему (см. рис. 2).

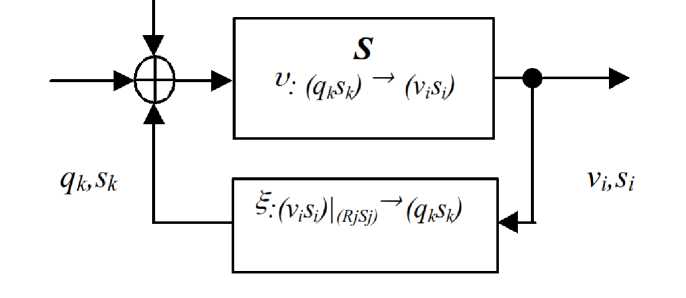
Рис. 2. Процесс идентификации и коррекции НС

Схема состоит из двух основных элементов:

• 1)    Собственно система, S, которая на входящие воздействия qk отвечает штатной работой либо сообщением о НС, Di.

• 2)    Контур обратной связи, обозначающий формирование корректирующего воздействия qk на основании сообщения о НС Di и гипотезы о её причине Tj.

Можно выделить следующие этапы коррекции НС в ПС:

• •    На основании сообщения Di, появившегося в элементе системы Si, строится гипотеза о причине НС Tj, относительно элемента системы Si, на основании которой формируется корректирующее воздействие qk на элемент системы Sk-

• Процесс формирования корректирующего воздействия qk по сообщению Di и гипотезе Tj задается отображением

£ ^: (^Di^,Si)|(r₃- ,Sj )      ^ ^(qk^,Sk ).                                              (2)

е Далее следует процесс проверки гипотезы о причине и соответствующего корректирующего воздействия. На практике это происходит путем выполнения действия qk по отношению к элементу системы Sk, в результате чего программная система выдает либо сообщение о НС D‘_i = dq, если гипотеза не подтвердилась, либо переходит в режим нормальной работы, о чем говорит сообщение dq. Формально процесс проверки гипотезы записывается следующим образом:

^{D : (q}k, ^Sk )  ^ ^(v‘i^,S‘i⁾.                                              (3)

Успешная коррекция НС соответствует справедливости соотношения

D’i = Dq.                                                 (4)

Без ограничения общности будем считать, что элемент dq € Уимеет семантическое значение «штатный режим работы», то есть отсутствие сообщений о НС. Нарушение соотношения 4 приводит к необходимости построения новой гипотезы о причине и её проверки.

• •    Описанные в н.п. 1, 2 этапы повторяются до тех пор пока не выполнится соотношение (4), либо пока не будут перебраны все элементы множеств R и Q. Если после полного перебора всех гипотез о причинах и всех действий по коррекции НС так и не устранена, то это означает, что в информационной базе процесса коррекции не хватает информации, и она должна быть пополнена извне. Тогда эксперт должен самостоятельно найти решение проблемы на основании своего личного опыта и интуиции и пополнить информационную базу процесса новыми данными.

Накопление информации в А происходит в виде прецедентов. Формальное определение прецедента как факта успешной коррекции НС дано в виде тройки:

Г = тф , Л. , ^, (5)

^Г = (Vi, Si ), ^ГІ = (Ti, ^S. ), тЕ = (Qi, ^), (6)

Di E V, Ti E R, Qi E Q, s' - ,s“ ,sj E S, ^

H^ ) = (^ ), (8)

где пары ( v₁,s^ ), ( t^s. ), (qi,s^q ) соответствуют некоторому сообщению щ, появившемуся в элементе системы s" , гипотезе о причине Ti, относящейся к элементу системы s. и действию по коррекции qi, примененному к элементу системы s^q. Множество, объединяющее все известные прецеденты, образует справочник прецедентов ф[ = {лф- E N n }, где N n = {0, ••• ,N - 1}.

Предполагается, что множество прецедентов, описывающих ПС, изначально не пусто, это предположение оправдано ввиду того факта, что все современные сложные программные системы поставляются вместе с технической документацией, в которой описываются предполагаемые неполадки и методы их устранения. На основе этого множества строится начальное множество значений системологических переменных. Элементы множеств информационного набора А образуют пространство альтернатив Н, заданное декартовым произведением множеств из А: Н = V х R х Q х S3.

Справочник прецедентов является подмножеством пространства альтернатив: П С -.

Изначально точки пространства Н и образующие их переменные не обладают никакими свойствами, поэтому для того, чтобы изучать содержательную взаимосвязь между прецедентами, необходимо искусственное введение некоторых отношений между элементами пространства Н, таких как частичная упорядоченность и метрическое расстояние между элементами.

При описании модели МКНС для установления отношений между элементами множеств значений переменных выбрана концепция иерархии, то есть вложенной системы классов эквивалентности.

Заметим, что формализуемый с помощью МКНС процесс является отражением процесса накопления и обобщения знаний эксперта о функционировании сложного программного обеспечения. На начальном этапе эти знания представляются как множество несвязанных информационных «квантов», и перед экспертом стоит задача построения взаимосвязей между ними. Одним из способов, обычно используемых в системном анализе, является построение иерархических отношений. По утверждению русского химика и философа Богданова, всё человеческое сообщество организовано в виде различных иерархических отношений. Это касается как общественного устройства, так и научного познания. В своей работе «Тектология: всеобщая организационная наука» он дал общее определение иерархических систем и привел многочисленные примеры из области естествознания и истории, в которых определяющую роль играют иерархические отношения. В соответствии с теорией Канта установление отношений между объектами внешнего мира (в данном случае - иерархических) - свойство человеческого разума, и люди переносят эти отношения на внешний мир в процессе его познания.

Программные системы очень сложны, множества значений переменных состоят из тысяч элементов. Наиболее естественным для человека способом изучать сложные системы является разбиение больших множеств на подмножества, которые потом дробятся далее. Таким образом, установление иерархических отношений - наиболее простой способ упрощения сложных систем.

Коль скоро мы приняли, что для эксперта как человека наиболее естественным способом изучения сложных систем является установление иерархических отношений, то будет разумным использовать для описания переменных МКНС именно эти отношения.

3.    Кодирование конечного множества прецедентов. Иерархическая метрика

В предыдущем параграфе мы определили прецедент как тройку переменных с конечным множеством значений (5), (6). В этом параграфе рассмотрим математическую модель, устанавливающую формальную запись переменных, задающих прецедент, построение метрического расстояния между значениями этих переменных и установление отношений порядка на этом множестве.

Строгая иерархия

Рассмотрим следующую систему разбиений некого конечного множества:

Q = {сд|г е Nn}(9)

на непустые непересекающиеся подмножества. Назовем разбиением нулевого уровня набор множеств

Но = ^0|г е No},(10)

q = q0.(ii)

Разбиение первого уровня задается соотношением

Н1 = {Q^ е Nn},(12)

Q1 С Q, Q|> 1,(13)

N 1 -1

Q = J Qi, V0 6 г = j 6 Ni - 1 ^ Qi QQi = 0.(14)

г=0

Далее, определим по индукции разбиение уровня I как

Н = {Q(|г е n^},(15)

Q^-1 = J Q^- |Q(|> 1,(16)

N; —1

q= J q(, vо 6 г = j 6 Nt -1 ^ q( Qq< = 0.(17)

г=0

И так до последнего уровня L:

:(18)

Hl-i = {Qf-1^ е Nnl-i},(19)

QL-1 С Q, |QL-1|> 1,(20)

N l - i - 1

q = J Qf—1, vo 6 г = j 6 Nl -1 ^ Qf Q qL = 0.(2i)

г=0

Определение 3.1

Назовем строгой иерархией П. определенной на конечном множестве Н, набор из L разбиений Н/:

Н = {НДг G N l } такой, что справедливы соотношения (9) - (21).

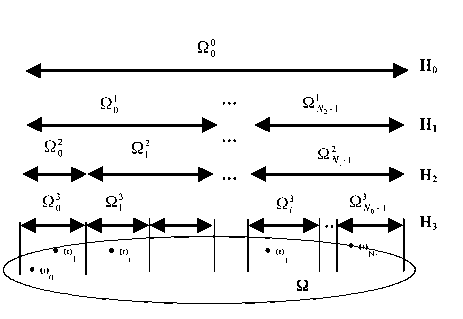
Рис. 3. Строгая иерархия Н, определенная на конечном множестве Н

На рис. 3 приведена иллюстрация понятия строгой иерархии, определенной на конечном множестве элементов. Уровни разбиений показаны рядами стрелок, обозначающими отдельные подмножества этих разбиений. На самом нижнем уровне показано само множество Н, состоящее из элементов top Разбиение верхнего уровня Но состоит из единственного множества Н0, которое совпадиет с множеством Н. Введем следующее ограничение, связанное со структурой последнего (или нижнего) уровня иерархии:

HL-1 = {ш,},                                       (23)

|HL| = 1 ,N l = N.                                 (24)

Смысл этого ограничения сводится к тому, что элементами последнего уровня иерархии (23) являются элементы множества. Данное ограничение не меняет смысла определения строгой иерархии, но позволяет формально описывать как само множество Н, так и элементы иерархии Н в однородньix терминах Ні.

Свойство 3.1. «Структура иерархии»

Структура иерархии Н задается числами

Xi = |Н<|,(25)

определяющими число элементов множества Ні, входящего в состав уровня иерархии Ну Очевидно, что для любого уровня Н^ перархии Н справедливо следующее соотношение:

N - 1

Е Xi = Nj+i.(26)

г=0

С учетом определения строгой иерархии (определение 3.1) и соотношения (7) легко показать, что

N0 = 1 6 N1 6 ... 6 N 6 N/+1 6 ... 6 Nl-1 = N.(27)

Очевидно, что для любого конечного множества Н можно определить различные строгие иерархии гН, оценим общее число возможных строгих иерархий, определенных на множестве Н. Итак, пусть множество Н содержит N элементов, оценим количество строгих иерархий с количеством уровней L, каждый из которых содержит N/ подмножеств. Как известно, число разбиений множества из п элементов на к непустых подмножеств определяется числом Стирлинга второго порядка:

к

^(п,к) = -^(-1)?(к - jT(28)

3=0

Таким образом, если принять, что разбиение нулевого уровня совпадает с самим мно жеством. то ость No = 1. то число вариантов Но равно

Wo = ДУ, No) = 1, No = 1.(29)

Далее, число различных разбиений первого уровня Hi определяется как

Wi =^(No,Ni).(30)

Продолжив цепочку до последнего уровня L, получим, что число различных строгих иерархий, соответствующих множеству с L уровней, каждый из которых содержит N/ подмножеств, определяется как

L-1

W = nw = П^' ,N3+1).                   (31)

3=о

Как видно из (31), количество различных строгих иерархий, которые можно определить на множестве из N элементов, исчисляется очень большими (с точки зрения ручного перебора) значениями, например, если N = N3 = 10, N2 = 3, N1 = 2, N3 = 1, то W = 27990. Таким образом, для любого конечного множества возможно определить строгую иерархию. Способ определения иерархии на множестве не рассматривается в МКНС, считается, что начальные иерархии задаются экспертом, а потом корректируются с учетом требований модели. Вместе с тем выбор начальных классификаций - очень важный вопрос, от того, как выбраны начальные иерархии очень сильно зависит эффективность применения модели.

Кодирующая функция. Кодовое множество

В этом пункте рассмотрим способ формирования кодов для обозначения прецедентов. Коды необходимы для сравнения прецедентов. Для того чтобы код прецедента однозначно представлял соответствующий ему прецедент, необходимо определить взаимнооднозначное соответствие между множествами кодов и множеством прецедентов. Для задания кодов прецедентов необходимо ввести между ними некоторые отношения эквивалентности так, чтобы эквивалентные прецеденты имели одинаковые коды. С другой стороны, важной задачей модели коррекции нештатных ситуаций является выделение классов прецедентов, обладающих некоторыми общими свойствами. Одним из наиболее простых способов задания классов является определение отношений эквивалентности. Рассмотрим способ установления отношений эквивалентности и порядка между элементами множества Q на основе понятия строгой иерархии.

Определение 3.2

Определим следующий набор бинарных отношений А^ между элементами множества Q. Будем говорить, что между двумя элементами из Q выполнено отношение ^гА^, если оба эти элемента принадлежат одному из подмножеств Q) разбиения Н^ строгой иерархии Н, определенной на множестве Q.

Ан = { А һ |г е N l },                                (32)

ⁱ А һ : ш} А һ w_k о w_d е Qi Л w_k е Qi, Qi е Щ .                     (33)

Ввиду того, что в соответствии с определением строгой иерархии множества Qi, принадлежащие уровню иерархии Щ_І, не пересекаются, соответствующее отношение ⁱ Ан является отношением эквивалентности, то есть симметричным, рефлексивным и транзитивным. Запишем этот вывод в виде следующего свойства.

Свойство 3.2. «Эквивалентность»

Все отношения, определенные в (32), являются отношениями эквивалентности. Классы эквивалентности этих отношений совпадают с подмножествами разбиений соответствующих уровней строгой иерархии (9) - (21).

Свойство 3.3. «Наследование эквивалентности»

Благодаря вложенной структуре классов эквивалентности отношений ⁱ Ан выполнено следующее утверждение:

Vz, m е N _l : г > m ^ ш/ А _һ ш ^ —> ш™ А _һ ш ^ .                 (34)

Определение 3.3

Определим на основе отношений, заданных с помощью (34), функцию кодирования элементов множества Q.

/_с Д ) = (Q° , Q1 ,..., п^ ), ш і е Q0 с Н о , ш і е Q11 с Hi ,

Wi е Q ^l _l с H l .

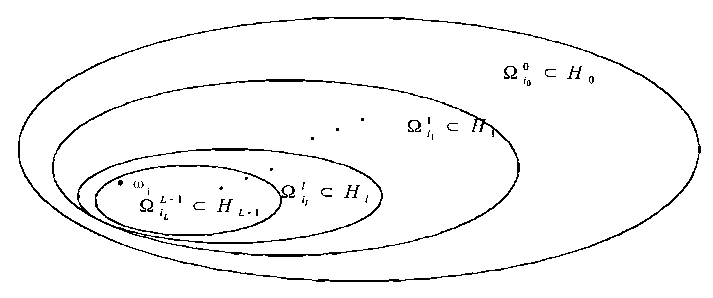
Рис. 4. Функция кодирования элемента множества ш ^ е Q

Смысл функции кодирования заключается в следующем. Элемент ш _і множества И кодируется списком или вектором, состоящим из имен классов эквивалентности, в которые входит элемент ші. Механизм кодирования проиллюстрирован на рис. 4. На рисунке изображена точка ші, элемент множества Q. Эта точка принадлежит набору вложенных классов Qi, показанных эллин сами. Код элемента ш і складывается из имен всех классов, включающих его, записанных в порядке взаимного включения этих классов эквивалентности. Покажем, что данное определение функции кодирования корректно.

Теорема 3.1

Определение 3.3 функции кодирования элементов ш множества И корректно, то есть функция кодирования обладает следующими свойствами'.

• 1)    V ш_г G И, VZ G N^ G Н : /Дш_г) = (И0о, И^,..., И^);

• 2)    V ш, G ИЗ!(И0о, И11,..., И^-) : /Дш_г) = (И0о, И1,..., И^-);

• 3)    ^{V Ш}2^,Ш^ ^{G И} : ^Ш^ = Ю j ^ Фс^(Шф = ФС^(Ш3 ).

Доказательство

• 1)    В соответствии с определением строгой иерархии (9) - (21) выполнено следующее -VZ G N l ^ И = Д^-¹ И,, это означает, что на любом уровне иерархии, любая точка ш, принадлежит хотя бы одному классу эквивалентности:

Vш^VZ G Nl ^ ЗИj с Н/ : ш, G И.

В соответствии с определением кодирующей функции (определение 3.3) это означает справедливость и. 1 теоремы.

• 2)    Допустим, что существуют различные наборы, кодирующие элемент множества ш,.

фс(ші) = (И0, И1,.... И^-1); /ДшД = (И0‘, И,1,..., И,—1), L~1                  -0^_1

покажем, что эти наборы совпадают.

• 1)    В соответствии с определением (35)

ш, G И00, шг G И11 .• • • ,шг G И^_11 ,(40)

ш, G И0’,ш, G И1,,... ,ш, G И^ 1.(41)

• 2)    Это означает, что

• Ио П И, = и,

И1П И1 = и. ИЗ)

:(44)

ИП 11   = и.<«)

• 3)    Но в соответствии с определением (9) - (21) классы эквивалентности не пересекаются. Следовательно,

  И0о =	И0, , го	(46)
  И11 =	= И11,	(47)
  		(48)
  L—1 И,1_1=	= Ий, —1. lL — 1	(49)

и функция /с(ш) определена однозначно.

• 4)    Доказательство третьего пункта следует из ограничений (23), (24), действительно,

^шг = ^шj  > ^И^_¹₁ = ^й-¹  ^ /с^(ш,) = fс^(шj )•

Теорема доказана. Как показано выше, множество представляет собой область определения функции f _с(ш) Определим множество значений этой функции следующим образом.

Определение 3.4

Назовем образ множества при отображении / _с(ш) определенном формулой (26), кодовым множеством О множества:

/с : О ^ О.                                      (50)

Обозначим элементы О квік щ:

О — {щ|^ е Уу}.

Данное определение проиллюстрировано на рис. 5. На рисунке исходное множество О показано в виде неправильной фигуры. Функция кодирования /с (ш) отображает О на множество кодов О, которое состоит из наборов (О0, О^,..., От-1), и показано прямоугольником.

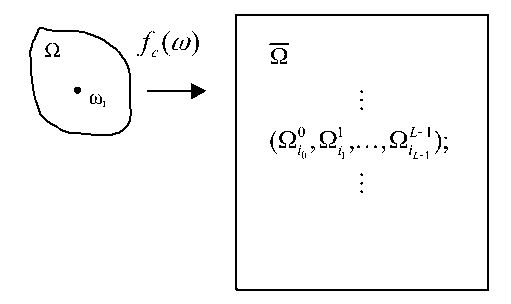
Рис. 5. Кодовое множество

В соответствии с определением кодирующей функции кодовое множество состоит из наборов вида (35). Кодирующая функция /с(Щ устанавливает взаимно-однозначное соответствие между множествами О и О.

Определение 3.5

Рассмотрим также множество О, образованное всевозможными наборами вида (О ⁷ -^, О ⁷ --^, ..., ОТ-1), I 6 L, О^ с Hj. Эти наборы представляют собой урезанные наборы, образующие множество О. Назовем множество О расширенным кодовым множеством для множества О:

О — {Щг1 — (О0о, О^,..., О^)г|г е Уу,1 е Ут},(52)

Щ — (О0О, Огі,..., Ог,, О+1,..., О^ )г е О,(53)

I 6 L, Оj. cHj.(54)

Легко показать, что данное множество наборов шгі взаимно однозначно соответствует множеству классов эквивалентности набора отношений А^ (32), то есть кодирует классы эквивалентности данных отношений. Определим отношение вложенности между элементами расширенного кодового множества. Смысл этого отношения заключается в том, что код одного из элементов, между которыми выполнено отношение вложенности, включает код другого.

Определение 3.6

Пусть ж = (е_о,е1,... ,€„) и у = (т]_о, тц, ..., т]_т) - элементы расширенного кодового множества. Зададим отношение вложенности Аь следующим образом:

жАьу О п >  т, V0 6 г 6 т ^ е^ = у .                    (55)

Таким образом, жА^у означает, что набор у вложен в набор ж. Легко показать, что отношение Аь удовлетворяет следующим свойствам:

• 1)    Vж,у Е И : жАьу, уАьж ^ ж = у (антисимметричность),

• 2)    Vж,у,z Е И : жАьу, уАьх ^ жАьх (транзитивность).

На основании этих двух свойств сформулируем следующее.

Свойство 3.4. «Частичное упорядочение»

Отношение Аь задает на расширенном кодовом множестве И строгое частичное уно-рядочение (И, Аь). Более того, с учетом структуры классов эквивалентности, заданной в (9) - (21), легко видеть, что

• Vж,у,z Е И : жАьу, жАьх ^ уАьх V хАьу,                     (56)

Зжо Е И : Vу Е И ^ жоАьу (существование наибольшего элемента).        (57)

В соответствии с теорией бинарных отношений отношение Аь, заданное в (55), является отношением древесного порядка (или древесным порядком). Таким образом, пара (И, Аь) задает дерево, а наибольшим элементом жо является класс разбиения И0 = И. Коды двух любых элементов расширенного кодового множества могут совпадать в части позиций. Зададим на расширенном кодовом множестве отношение, которое определенным образом упорядочивает все элементы расширенного кодового множества по количеству позиций в их кодах, совпадающих с позициями в коде некоторого фиксированного элемента данного множества.

Лемма 3.1

Для любых двух элементов ш^ ,cuj,i_j расширенного кодового множества И существует единственное целое число п*, называемое уровнем разделения, такое что:

—

Vw,^ ,Д,ц Е И ^ 3!п* : 0 6 п 6 L — 1,(58)

Vk : 0 6 к 6 п* ^ ш^АДД,(59)

Vk : п* < к < min(lj,lj) ^ -(^5^А^сщ).(60)

Доказательство следует из свойства наследования эквивалентности (свойство 3.3) и ограничения (23).

На нижнем уровне иерархии эквивалентности нет, на нулевом - есть, следовательно, существует уровень, на котором эквивалентность появляется в первый раз, а потом сохраняется в силу (34). Единственность доказывается от противного. В диапазоне между двумя предполагаемыми уровнями нарушается выполнение требований определения одного из них, из чего легко сделать вывод, что они совпадают. Лемма доказана. Будем считать предыдущую лемму определением уровня разделения двух элементов расширенного кодового множества. Итак, для любой пары элементов кодового множества существует уровень разделения п*. Зафиксируем отдельный элемент ж* и определим для него отношение ^ж* Л/ между любыми двумя элементами у и z кодового множества.

Определение 3.7

Назовем отношением дальности ^х* At между элементами х и у расширенного кодового множества отношение, удовлетворяющее следующему условию:

у ^х *Atz О Z(x*,у) 6 Z(x* ,z ).                                 (61)

Легко показать, что отношение дальности х* A_t удовлетворяет аксиомам линейной упорядоченности. Соответственно, будем называть это отношение также порядком близости. Введем обозначения:

X * л              tx*

ух Atz А—¥ у У z, у Abz О уУ-z.

На рис. 6 показан пример фрагмента графов отношений вложенности и близости, определенных в данном параграфе. В нижнем ярусе дерева показаны элементы кодового множества (коды прецедентов), более высокие уровни представляют расширенное кодовое множество (усеченные коды прецедентов). Отношения вложенности показаны на рисунке сплошными стрелками. Пунктирными стрелками показано отношение порядка близости к фиксированному элементу х*, изображенному в центре нижнего яруса.

Понятие уровня разделения и отношение близости наглядно трактуются с точки зрения записи элементов расширенного кодового множества. Если два элемента расширенного кодового множества х и у имеют уровень разделения Z*, то их записи в виде наборов х = ( е _о , £1,..., е_п )^и у = (ц_о, щ,..., Лт ) совпадают в части первых Z* составляющих:

Z(x,у) = Z* О Ег = Л , v 0 6 г 6 Z* .                            (64)

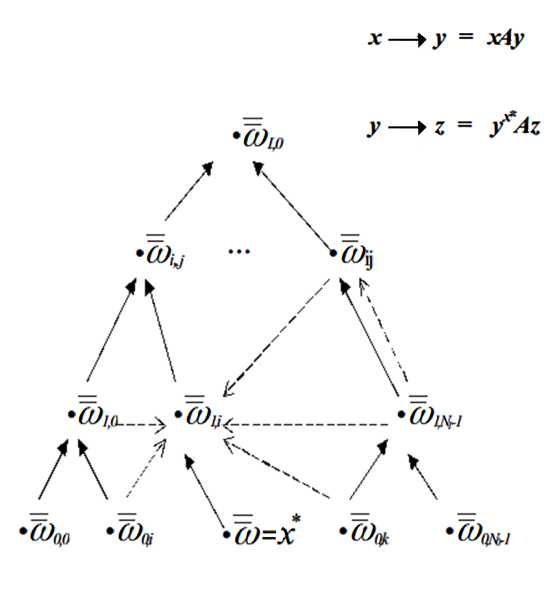
Рис. 6. Фрагменты графов отношений х* A _t и A b

Операции со строгой иерархией как деревом

Как было показано, расширенное кодовое множество и определенные на нем отношения могут быть представлены в виде древовидного графа, или дерева. Вершины этого графа назовем узлами дерева. В узлах дерева находятся элементы расширенного кодового множества. Ветви дерева соответствуют элементам кодового множества, представляющего исходное множество И. Введем обозначения.

Н - всё дерево целиком.

Нк - множество всех эле ментов дерева уровня к, то есть собственно уровень к совпадает с уровнем строгой иерархии (определение 3.1), Хк - некоторый э.тсмсит уровня к.

һк - некоторое подмножество элементов уровня к, һк С Н_к,

Хк ~ поддерево дерева. Н. имеющее своим верхним элементом х_к.

һк~ часть дерева Н. состоящая из всех поддеревьев Хк- с верхними элементами Хк С һк,

Нк - часть дерева, состоящая из уровней ниже к — 1.

Хк - часть элемента х Е И, состоящая из составляющих х^ : 0 6 г 6 к — 1, һк - часть дерева, состоящая из всех Хк : Хк Е һк,

Нк - часть дерева, состоящая из всех уровней от 0 до к — 1.

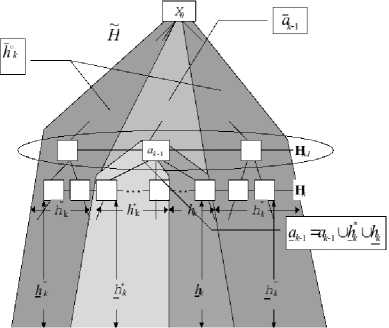
Рис. 7. Дерево расширенного кодового множества.

Рассмотрим разбиение дерева, как показано на рис. 7, по отношению к элементу Ок-1 уровня к — 1. Всё дерево, таким образом, распадается на следующие множества:

Н = һк и һк и һк и а_к-1 и а_к-1 и һ*_к и һ_к U һ*_к U һ_к .

Множества һ_ки һк отличаются лишь тем, что одно из них составит основу для введения нового уровня в дерево классификации, в остальном же они равноценны. Запишем условия на уровень разделения п* для пар элементов из областей, заданных соотношением (65):

Таблица!

	«к-іи Пк-1	Һ * һк	һк	Һ * һк	һк
һк и һк и һк	п* < к — 1	п* < к— 1	п* < к—1	п* < к — 1	п* < к — 1
«к-1и Ок-1	п* < к — 1	п* = к—1	п* = к—1	п* = к — 1	п* = к — 1
Һ * һк		п* = к—1	п* = к—1	к 6п* 6 к—1	п* = к — 1
һк			п* = к—1	п* = к — 1	к 6 п* 6 к—1
Һ * һк				п* >к — 1	п* = к — 1
һк					п* >к — 1

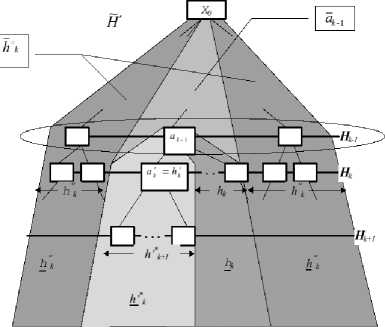
Рис. 8. Добавление уровня дерева.

Процесс добавления уровня показан на. рис. 8, сутв его заключается в следующем: все элементы ж. С h. объединяются в одну новую категорию, между этими элементами и узлом a.-i вставляется новый узел а.- В результате происходит следующее преобразование множества элементов, входящих в класс a.-i:

^к = {ak};(

Vi : N>i>k -^ h* = h*-1;(67)

hi = U hl = ak U hl-i.(68)

i>ki>k

Операцию удаления уровня в дереве можно определить в обратном порядке. При выполнении этой операции один из узлов удаляется, а. его наследники автоматически становятся наследниками его родителя.

• 3.1.    Иерархическое расстояние между элементами расширенного кодового множества

В предыдущем параграфе на. основании понятия строгой иерархии, определенной на. множестве П, было построено расширенное кодовое множество П, состоящее из наборов с длинами, не большими количества уровней L определеиной на П строгой иерархии Н. Между элементами расширенного кодового множества были установлены отношения вложенности и близости, являющиеся отношениями частичной упорядоченности. В этом параграфе определим на. базе введенных отношений функцию расстояния между элементами расширенного кодового множества, и покажем, что эта. функция удовлетворяет аксиомам метрики.

Определение и свойства иерархического расстояния

Рассмотрим два элемента ж и у из расширенного кодового множества ж = (ao, ai,.. .аПх), у = (bo, bi,... ЬПу).                                  (69)

Определим для каждого уровня строгой иерархии Hi модуль уровня тд mi = 2L-i, 0 6 i 6L - 1.                                (70)

Определим расстояние между составляющими одного уровня следующим образом: расстояние равно нулю, если составляющие совпадают (то есть соответствующие элементы множества И принадлежат одному классу эквивалентности отношения 1А^), и единице, если нет:

I“/^ыИ О ' = £;                        (71)

и, О / = »1 •

Определенный в (57) уровенв разделения с учетом понятия расстояния между составляющими (71) записывается следующим образом:

Уж, у G И ^3 !п_ху* : 0 6 п * 6 min {п_а, щ} ,

V п_ир :    0 6 п_ир 6 пав * ^ |а_Ицр, Ь_Пир | = 0,                          (72)

Vn dn :    пав * <  n_dn 6 max {п_ж,п_у } ^ |« n _dn, b_ndn | = 1.

С учетом введенных обозначений определим расстояние между элементами расширенного кодового множества следующим образом.

Определение 3.8

Назовем функцию dh, определенную на множестве И х И, иерархическим расстоянием между элементами расширенного кодового множества:

max{nanb } dh(ж,у) = |ж,у|=   У^   тп •|a„,b„|.

n=0

Рассмотрим связь иерархического расстояния d_d(x,y)v и уровня разделения п*(ж,у) Разбив сумму, представленную в (65), на две части, одна из которых представляет составляющие до уровня разделения, а вторая - после него, получаем в соответствии с (64):

max { n _x ,n_y }                  п Ав          max { n _a n b}            max { n _a n ^}

|ж,у| =   £   mn •|а_n,b_n|  У • 0+  £   т_п • 1=  £  2^-

n=o                  n=o           ⁿ AB +i             ⁿ AB +i

Упростив выражение (74), получаем

|ж,У|

max{n_xn_y }

^ ^    2^- n _ 2^ — n * (i _ 2 П *— max { n ^ n _y}) _ 2^~n*

2^- max { n ^ n _y }

ⁿ xy + 1

Если разбить все пары элементов на группы с одинаковым п*, то для каждой пары реализаций внутри такой группы (см. рис. 9) все уровни дерева можно разбить на две области: 0 6 Пу 6 п_х.

В этой области расстояние |ж,у| определяется значением пх, то есть не зависит от Пу:

|ж,у| = 2L-n* _ 2L-n",

п_х< Пу 6 L.

Начиная с уровня пх, значение расстояния нарастает со скоростью перевернутой обратной экспоненты, приближаясь к асимптотическому значению.

|ж,у| = 2 ^{L - n} * _ 2 ^L - ⁿ ------> 2 ^{L - n} * _ 1.

nx ^L

На графике (см. рис. 10) показаны изменения расстояний внутри различных групп с различными п * для иерархии с L = 6.

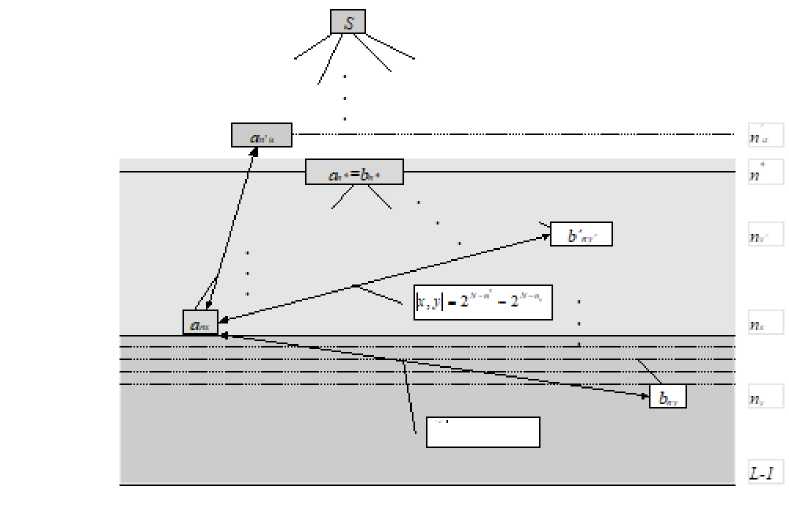
Рис. 9. Иерархическое расстояние между элементами расширенного кодового множества.

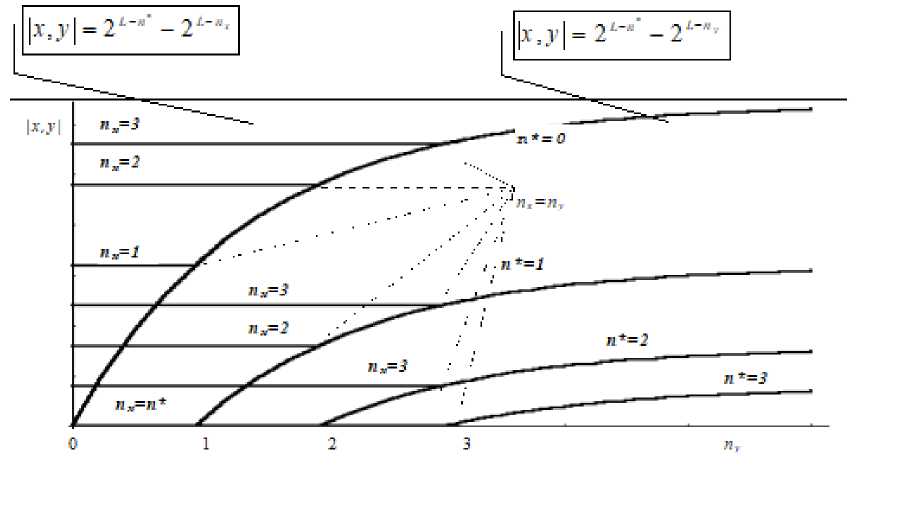
Рис. 10. Расстояния между различными группами точек в расширенном кодовом множестве с L = 6

Пример 3.1

Рассмотрим иерархию с L = 5 и нарисуем распределение расстояний между фиксированным элементом А и всеми остальными элементами дерева. «Нулевой элемент», расстояния до которого мы измеряем, обозначен на. рис. 11 серым цветом. Внутри прямоугольников, обозначающих узлы дерева, стоят числа, равные расстоянию от этих узлов или листьев до «нулевого листа». На рисунке видно, что при уточнении элементов, расходящихся с эталонным (белые узлы и листья), расстояние до эталонного листа, увеличивается, а при уточнении элементов, не выходящих за пределы эталонной, но не совпадающей с ней (серые узлы), это расстояние уменьшается.

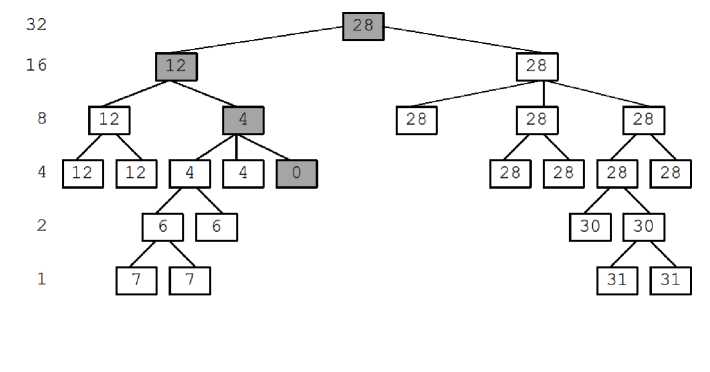
Рис. 11. Иерархическое расстояние между элементами расширенного кодового множества.

Проверим выполнение аксиом метрики для определенного с помощью формулы (73) расстояния.

Лемма 3.2. Свойства неотрицательности и невырожденности

Уж,у € И ^|ж,у| > 0, |ж,у| =0 О ж = у.

Доказательство

По определению (73), расстояние между двумя элементами А и В дерева есть сумма произведений модулей уровней на. расстояния между А и В внутри каждого уровня. Как модуль уровня (70), так и составляющая расстояния внутри этого уровня (71) - неотрицательные числа, следовательно, сумма, их произведений также неотрицательное число. Как следует из формулы (70), модуль уровня һ_п > 0, следовательно:

тах { п _ж п _у }

|ж,у| = У^    һ_п •|а „ ,Ь „ |= 0 О У 0 6п 6 тах{п_ап_ь} ^ |а_п,М =0 О (78)

п=0

О У 0 6 п 6 тах{п_ж,п_у} ^ а_п = Ь_п О ж = у.

Лемма доказана.

Лемма 3.3. Свойство симметричности —

Уж,у € И ^ |ж,у| = |у,ж|.

Выполнение этого свойства, очевидно из соотношений (70) и (71).

Лемма 3.4 Неравенство треугольника

У ж,у, д € И ^|ж, д| 6 |ж,у| + |у, д|.

Доказательство

Рассмотрим три произвольных элемента расширенного кодового множества ж, у и д. В силу соотношения (75) парные расстояния между этими элементами можно записать в следующем виде:

|ж,у| 2 ^l "' ■ *

_ 2 L — тах { п _ж Л у}

|у,д| = 2 ^l '" ■

_ 2 L — max { n _y n ₂ }

|ж,г| = 2 ^{L — n}■

' Xz

*

^L— max { n _ж n z }

Рассмотрим соотношение, полученное после операции (80) + (81) - (82). Требуется доказать, что результат всегда неотрицателен.

Предположим, что

^ПХу > ⁿyz ^,п х > Пу .

Данное предположение не ограничит общности доказательства, так как расстояние симметрично относительно ж и у. Итак,

6 =

|ж,у| + |у,2| - Д,^

= 2^{— n} ^,y + 2^{— n} y,^z — 2^—п^

2L

— тах { п _ж ,п у}    q— max { n _y ,n z} ■ q— max { n _ж ,n z}

В соответствии с определением уровня разделения п * (72) и соотношением (83) очевидно, что

*** ⁿ xz    ‘^z   ^пху^.

Следовательно, с учетом (86), правую часть (85) можно переписать в виде

6 = 2—п^у — 2 — тах { п ^ ,п у} _ 2— max { " y п } + 2 max { n _ж ,n z}

Рассмотрим теперь различные случаи соотношения п_х, Пу и n_z с учетом соотношения (83):

• 1)    Pz > П_х > Пу.

Тогда оцениваемая разность имеет вид

• 6 = 2^—пД _ 2^{— п} - - 2^{— п} + 2 ^п = 2^—<у - 2 ^п = |ж, у| > 0.

• 2)    П х > nz > Пу.

• 6 = 2^—пД - 2^—п^ - 2 ^п + 2^—п^ = 2^—<у - 2 ^п ,

п * _у 6 п_у 6 n_z ^ 2^—п^у > 2^—пz ^ 6 >  0.

• 3)    п _х > Пу >n_z.

• 6 = 2^—<у - 2^—п^ - 2^—п^ + 2^—п^ = 2^—п^у - 2^—п^ ’

п Х _у 6 П у ^ 2^—п^у > 2^—пу ^ 6 >  0.

Итак, мы доказали, что 6 > 0.

Лемма доказана.

На основании доказанных выше свойств сформулируем следующую теорему.

Теорема 3.2

Иерархическое расстояние d^ : И х И ^ Z, определенное в (73), является метрикой, то есть

• 1)    Уж, у G 12 ^ |ж, у| > 0, |ж, у| = ⁰ О ж = у;

• 2)    Уж, у G ИИ ^ |ж,у| = |у,ж|

• 3)    У ж,у,2 G И ^|ж,г| 6 |ж,у| + і у,2 і

Доказательство теоремы следует из утверждений лемм (лемма 3.2-лемма 3.4).

Изменение расстояний между элементами иерархии при изменении её структуры

Перейдем теперь к рассмотрению того, как изменятся парные расстояния между элементами дерева после добавления уровня, описанного в п. 3.1.3. В соответствии с соотношением (75) расстояние между элементами а и Ь определяется параметрами п*_ь, п _а ил и пь Для того чтобы определить, как изменится расстояние в паре элементов, необходимо рассмотреть изменение этих параметров. Очевидно, что п _а и пь могут измениться, только если соответствующий элемент принадлежит h* U h*, с п*_ь ситуация более сложна. Рассмотрим по аналогии с (65) табл. 2, описывающую различные варианты размещения пар элементов а и Ь.

Т а б л и ц а 2

b € \ a G	Д-І^Д-І	V		V
b” иДіиаы	«„V = дЛ д- = д; »„  = пь-	д-/=д/; д- =д; n„ =nb* *•	»QV =дЛ д = д; Ну = Д-	Д'у' ^дЛ д- = я.,; пь. = пь + 1.	д-у’ = дЛ д. =д; Ну = пь.
V	««V = «ab\ »a- = Д +1;	Д-у' = ПаЬ + 1 = k; na. = no +1; ny = nb*V	^'Ъ- = Яаъ = = 4-1; па. = па +1; «V =»ь-	д-у' = д/ + һ д- = д +1; д- = д+L	«.•к* = д/ = = 4-1; Д' = Д +1» «у =Д-
	"a'J = «ah’; na. = nu; п„ ="b-	".V = n-b = = 4-1; ".• = "a; nb. = Д + 1.	^.ь* ^nJ; «а. = иа; Ну =«ь	д/ = д = = 4-1; д- = д; д. = д + 1.	Д'у* = д/; д- =д; Ну =Д-
	n,V = nab", na, = na +1; «6- = nb-	«.V =nOb +i; П , = Д + h Д = Д + L	^■Ь' = "ob = = 4-1; иа> = иа +1; Пу =»к.	д-у* = д/ +1; Д- = д +1; д. = д + 1.	Д'у* = д/ = = 4-1, д. = д +1; «у = Д-
	”.V = < = = 4-1; Па' = ДІ nb, = Д +1	n.v = < = = 4-1; »Q.   ~ Па> nb. = nb + Y	иД'у* = V; Д' = д; Ну = Д-	Д-у" = д/ = = 4-1; Д' *Д’ пь, = д +1.	Ду* = д/; Д' =д; Ну =Д.

Соответственно этим соотношениям изменятся и парные расстояния между элементами расширенного кодового множества. Следующий пример иллюстрирует приведенную выше схему изменения парных расстояний при добавлении уровня.

Пример 3.2

2L-max{n'a,nb}

2L- max {n_a +1 ,nb}

Добавим новый уровень прямо над эталонным листом, объединив его в общую группу с соседним узлом, но оставив третий узел на том же уровне. На рисунках видно, как изменилось распределение расстояний внутри дерева.

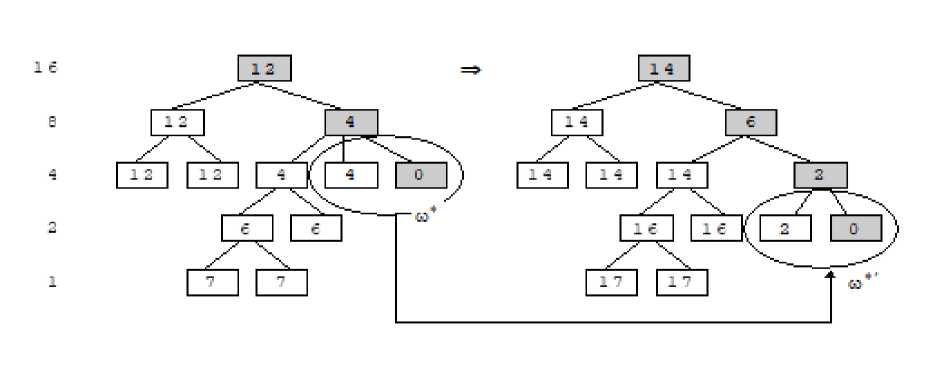
2. a Е К

Kbl /

= 2 ^L —n*

-

П . = П . , |a, bl = 2

п*'

, L-n*

2 L - max { n _a ,п _ь }

= П*, Пь =п_ь + 1,

2 L - max { n _a ,n _b +1 }

-

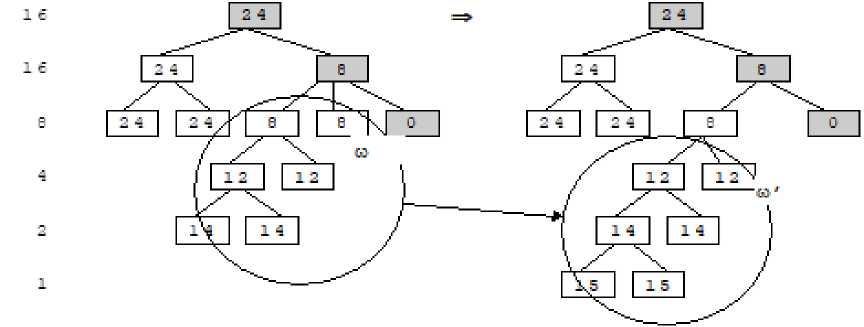
Связь иерархической метрики и порядка близости

Определенное индивидуальное отношение ж*А^ (определение 3.7) устанавливает отношения между элементами расширенного кодового множества относительно фиксированного элемента ж*, принадлежащего этому же множеству. Как было показано, это отношение является линейной упорядоченностью. Построим ещё одно отношение порядка, созданное на основе иерархической метрики.

Определение 3.9

Назовем отношением иерархического метрического порядка индивидуальное отношение, сравнивающее расстояние от элементов у и г расширенного кодового множества до фиксированного элемента ж*:

_ *                dx*                                   .

у А, г Оу ^ г О d_h(x ,у) >d_h(x,z).

Легко показать, что данное отношение является отношением линейного порядка на расширенном кодовом множестве, в силу того, что иерархическое расстояние (73)

удовлетворяет аксиомам метрики.

Теорема 3.3

Для любых двух элементов у u z из расширенного кодового множества из справедливости отношения порядка дальности следует выполнение отношения иерархического метрического порядка при фиксированном элементе х*, задающем эти отношения.

tx*        dx*

Уу, z,x Е И ^ у Д z ^ у Д Z.

Доказательство следует из формулы для определения расстояния и соотношения между уровнем фиксированного элемента и элементов у, z. Обратное следствие выполняется не всегда, можно лишь показать, что справедливо только нестрогое следствие:

dx*        tx*

Уу, Z, X Е И ^ у Д Z ^ у Д Z.

4.    Заключение

В статье представлен подход к построению метрического пространства на множестве прецедентов, возникающих в процессах коррекции нештатных ситуаций при эксплуатации сложных программных систем. Данный подход может применяться и для любых других множеств прецедентов, в которых возможно построение строгих иерархий. Построенное метрическое пространство и определенная в нем иерархическая метрика позволяют определить в пространстве прецедентов отношения близости и порядка и задавать в нем алгоритмы поиска по критерию близости между прецедентами.