Межпозиционное отождествление результатов измерений и определение координат воздушных целей в многопозиционной радиолокационной системе в условиях многоцелевой обстановки

Постановка задачи

Рассмотрим МПРЛС, состоящую из М синхронизированных специализированных пере- датчиков TRi, расположенных в точках с координатами приемников RSj, расположенных в точках с координатами

( x T , y TR , z T ) , где i=1, 2, ..., М , и N ( x RS , y RS , z R ) , где j =1, 2, ^, N , в зоне

действия которой одновременно находятся K целей Tm, где m=1, 2 … K. Суммарные дальномер- ные измерения осуществляются по (MxN) бистатическим звеньям «TR – RS» (рис. 1).

В каждом бистатическом звене наблюдаются отклики от K целей, траекторные параметры которых априорно неизвестны. Суммарные измерения дальности по сигналу от i-го передат- чика TRi, рассеянному m-й воздушной целью Tm и принятому в j-м приемнике RSj, будут иметь вид

jm = rT + rRm + E ,                                                       (1)

где     C =[( X T - X m ) ² + ( y TR - У т ) ² + ( z TR - Z m ) 2 Г     ^- Дальность пути « TR-T_m »;

RS        RS       2 RS        2 RS       2^1/2

Г т m =L^{( X} j — x m ) ^{+ (} У , — У т ) ^{+ (} z j — z m ) J — ДаЛЬНОСТЬ ПУТИ « T m -RS j », ( X m , y ^, , Z_m ) — KOOp — динаты m -й воздушной цели T_m ; ε – случайная погрешность измерения дальности.

В ходе процесса первичного межпозиционного отождествления результатов измерений в МПРЛС необходимо все суммарные измерения дальности по сигналу от передатчика TR_i , рассеянному m -й воздушной целью T m и принятому в приемнике RS j r _j ⁱ _{, m} , поставить в соответствие нужной цели T_m , сформировать K векторов измерений R _m , где m =1… K , грубо определить координаты всех K наблюдаемых целей и подготовить исходные данные для завязки траекторий.

Способ межпозиционного отождествления измерений и определения координат целей в МПРЛС в условиях многоцелевой обстановки

Наиболее широко известен способ первичного межпозиционного отождествления результатов измерений в МПРЛС, основанный на прямом переборе всех возможных гипотез отож- ( N ■ M - 1 )

дествления [1]. Однако в этом случае потребуется проверить (K !)      гипотез, для каждой из которых вычислить координаты K целей с использованием известных методов (например,

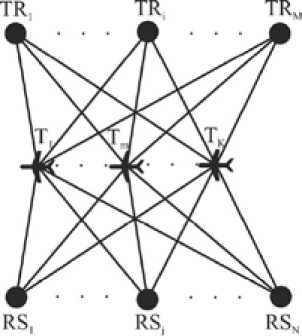
Рис. 1. Конфигурация МПРЛС в горизонтальной плоскости в условиях многоцелевой обстановки

Fig. 1. Configuration of multisensory radar in a horizontal plane in multitarget conditions

метода наименьших квадратов). При этом количество гипотез, а следовательно, и потребные вычислительные мощности быстро растут с увеличением количества наблюдаемых целей [1].

Для сокращения количества ложных гипотез применяется предварительное стробирование по координатам и параметрам, для чего необходимы дополнительные избыточные измерения, например, в дальномерных измерительных системах необходимо измерить и азимут цели [1].

Предложенный способ первичного межпозиционного отождествления обеспечивает сокращение количества гипотез отождествления и не требует при этом дополнительных избыточных измерений. Способ основан на виртуальном обзоре пространства [3] по координатам x и y с шагом, соответствующим разрешающей способности МПРЛС по дальности. При этом на каждом шаге сканирования в пределах зоны действия МПРЛС тем или иным способом задается предполагаемое (гипотетическое) местоположение цели на плоскости T^H(x,y) . Предполагаемую высоту цели выбирают фиксированной, соответствующей середине зоны действия МПРЛС по высоте z . Для предполагаемого местоположения цели рассчитывают предполагаемые суммарные дальности в каждом бистатическом звене « TR_i - T^H - RS j »:

rr j ( x , y ) = [ ( - x )² + ( y TR - y )² + ( z iR - z )² ] ^1/2 +

RS         (v^RS         (S^RS    tVI¹'²

+l_( xj - x) + (yj - y) + (zj - z) ] .

Для соответствующего бистатического звена из K действительных измерений r _j ⁱ _{, m} выбирают измерение, наилучшее по критерию минимизации модуля невязки между предполагаемым и действительным измерением:

m = arg min(| rr j ( x, y ) - r j , „ |) .

Для всей МПРЛС, т.е. для всей совокупности бистатических звеньев, для предполагаемого местоположения цели определяется суммарная невязка:

MN

A r^ ( x,y ) = ZE| ^rrj ( ^x , У ) - ^ri,m |. i = 1 j = 1

Проверка наличия цели в предполагаемом ее местоположении TH(x,y) осуществляется после виртуального сканирования всей зоны действия МПРЛС и только в точках минимума суммарной невязки. Для обострения минимумов и лучшего их выявления целесообразно использовать логарифм от значения суммарной невязки. В этом случае проверка наличия цели будет осуществляться в точках (.x,y), определяемых в соответствии с выражением d2 lg (A rE(x, У ))   = 0

dxdy      x=x y=y

При этом минимумы суммарной невязки будут формироваться для каждой из K наблюдаемых целей, а также для ложных целей.

Для исключения ложных целей значение функции в проверяемых точках минимума lg ( A r ^ (. x , y ) ) сравнивают с порогом h , величина которого определяется с учетом погрешности

A_E дальномерных измерений, погрешности A _xy , обусловленной конечным значением шага виртуального обзора пространства по координатам x и у , а также погрешности A _z , обусловленной неточностью определения высоты целей, для каждого бистатического звена:

h = lg (n • M-(ae +A x , y +A z)). (6)

Погрешность дальномерных измерений определяется как максимальная ошибка измерений

A_e = 3 ^ , (7)

где σ _ε – среднеквадратическое отклонение (СКО) случайной погрешности измерения дальности ε, распределенной по нормальному закону с нулевым математическим ожиданием.

Погрешность, обусловленная конечным значением шага виртуального обзора пространства, определяется как наибольшее удаление цели от проверяемой точки с учетом, что проверяемая точка соответствует центру ячейки обзора пространства, а цель находится в ее узле:

A x , у = ^( 0.5 А x ) 2 + ( 0.5 A у ) 2 , (8) где A _x и A _y - величина шага виртуального обзора пространства по координатам x и у соответственно.

Погрешность, обусловленная неточностью определения высоты целей, может быть определена как максимальная разность хода лучей « TR – T – RS » для случаев, когда цель находится на средней высоте z и у поверхности земли:

A z

= 2 ( ( О.5 L ) 2 + z²

—

0.5 L ) ,

где L – база МПРЛС (расстояние между линией передатчиков и приемников).

Принятие окончательного решения о наличии ( 0 = 1 ) или отсутствии ( 0 = 0 ) цели в проверяемой точке пространства осуществляется в соответствии с правилом

lg (a rz(x,у ))

> h ^ 0 = 0

< h ^ 0 = 1

Координаты проверяемых точек ( x, у ) , для которых выполняется правило (10), являются грубой оценкой координат наблюдаемых целей ( x m , у m ) .

Вектор измерений R _m для каждой m -й воздушной цели T m будет сгруппирован из измерений r i m , обеспечивающих минимум суммарной невязки lg ( A r ^ ) в соответствующей точке ( x m , ^у m ) .

Точное определение координат каждой m -й воздушной цели T_m осуществляют на основании сформированных векторов измерений R _m одним из известных методов, например методом наименьших квадратов [9].

Таким образом, эффективность предложенного способа в сравнении с прямым перебо- ром всех возможных гипотез определяют сокращением количества проверяемых гипотез с

( K f f ^{NM —} 1 )

до одной.

Методика исследования эффективности способа межпозиционного отождествления измерений и определения координат целей в МПРЛС

Исследование эффективности способа межпозиционного отождествления измерений и определения координат целей в МПРЛС было проведено методом имитационного моделирова- ния. Структурная схема имитационной модели приведена на рис. 2.

В блоке 1 задается конфигурация МПРЛС путем определения матрицы X ^TR координат передающих позиций ( x TR , y TR , z ™ ) , где i =1, 2, ..., М , и матрицы X RS координат приемных позиций ( x RS , y RS , z R ) , где j =1, 2, .., N . В блоке 3 задается матрица X ^T координат воздушных целей ( x m , y m , z m ) , где m =1, 2, ., K. В блоке 2 на основании заданной конфигурации МПРЛС и заданных координат одновременно наблюдаемых воздушных целей в соответствии с (1)

для каждого бистатического звена для каждой цели рассчитывают суммарные измерения дальности rji,m по сигналу от i-го передатчика TRi, рассеянному m-й воздушной целью Tm и принятому в j-м приемнике RSj с учетом заданного СКО погрешности дальномерных изме- рений σε.

В блоке 4 в пределах зоны действия МПРЛС с заданным шагом по координате x и коорди- нате y на средней высоте z задают предполагаемое местоположение цели TH(x,y). В блоке 5 для предполагаемого местоположения цели в соответствии с (2) рассчитывают предполагаемые суммарные дальности rrj (х, у) в каждом бистатическом звене «TRi-TH-RSj». Вычисление модуля невязки между предполагаемым и действительными измерениями в каждом бистатическом звене осуществляется в блоке 6. При этом из K действительных измерений rji,m выбирают измерение rji,mˆ , наилучшее по критерию (3).

В блоке 9 в соответствии с (4) определяют логарифм суммарной невязки lg ( A r ^ ( х , у ) ) и в соответствии с (5) определяют точки ( X_m , у_m ) , в которых его значение будет минимальным. Полученные минимальные значения lg ( A r _s( X, у ) ) в блоке 8 сравнивают с порогом h , значение которого рассчитывают в блоке 7 на основании известных Δ x , Δ y , z , σε. Если значение lg ( ^A r z ( X, У ) ) удовлетворяет условию (10), то по сигналу 9 = 1 в блоке 11 координаты соответствующей точки ( X, у ) , поступающие из блока 4, выбирают в качестве грубой оценки ко-

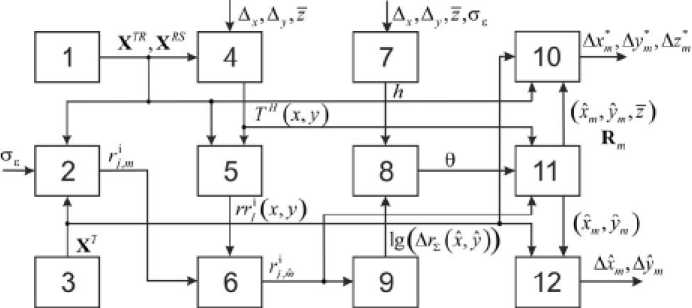
Рис. 2. Структурная схема имитационной модели

Fig. 2. The block diagramme of imitating model ординат наблюдаемой m-й воздушной цели (x*, у* ). При этом вектор измерений R* для m-й воздушной цели Tm будет сгруппирован из измерений rji,mˆ , поступающих из блока 6.

Непосредственная оценка эффективности предложенного способа в плане определения координат целей заключается в сравнении в блоке 12 полученных оценок координат ( x * , у * ) целей на плоскости с заданными координатами воздушных целей ( x_m, у * ) , поступающими из блока 3, и формировании сигналов рассогласования Ax * , A у * .

Для оценки эффективности межпозиционного отождествления измерений предложенным способом сформированные векторы измерений R _m используют в блоке 10 в качестве исходных измерений для более точного метода определения координат (метода наименьших квадратов), при этом полученные грубые оценки координат целей ( X * , y * , z ) применяют в качестве начального приближения для получения точного решения координатной задачи ( х * , y m , z * ) этим итерационным методом. Степень отклонения A x * , A y * , Az * полученной точной оценки ( x * , У * , z * ) от заданных координат ( x * , y * , z * ) воздушных целей используется в качестве критерия эффективности межпозиционного отождествления измерений в МПРЛС.

Результаты численного эксперимента

В соответствии с описанной методикой численный эксперимент был проведен для МПРЛС, состоящей из М=3 передатчиков и N=3 приемников, разнесенных на ширину базы L =40000 м. В зоне действия МПРЛС одновременно находятся K=7 целей. Координаты воздушных целей в локальной системе координат, за начало которой принят центр МПРЛС, а также координаты приемных и передающих позиций МПРЛС приведены в табл. 1.

Геометрия численного эксперимента на плоскости показана на рис. 3, где передающие позиции обозначены квадратами, приемные позиции – ромбами, а кружки демонстрируют истинное местоположение воздушных целей.

При численном моделировании использовали следующие значения параметров:

СКО случайной погрешности измерения дальности С_Е = 10 м;

величина шага обзора по координатам x и у A x = A y = 100 м;

середина зоны действия МПРЛС по высоте соответствует Z = 1000 м.

На рис. 4 показано полученное в ходе моделирования поле логарифма суммарной невязки lg ( A r _s( x , у ) ) . Видно, что на графике наблюдаются восемь основных минимумов (обозначены цифрами 1 – 8), семь из которых соответствуют семи истинным целям, а один – ложной цели.

Полученные точки ( x * , у * ) , в которых значение логарифма суммарной невязки lg ( ^A r _s( x,у ) ) минимально, изображены на рис. 3 шестиконечными звездами. Видно, что пер-

Таблица 1. Координаты целей и позиций МПРЛС

Table 1. Coordinates of the targets and of the positions of multisensory radar

Коорд.	TR 1	TR 2	TR 3	RS 1	RS 2	RS 3	T 1	T 2	T 3	T 4	T 5	T 6	T 7
x, м	0	-20000	20000	0	-20000	15000	6050	8030	17090	-10040	-15070	-5010	10120
y, м	20000	17000	25000	-20000	-20000	-22000	10070	-1010	5080	7150	8090	-5070	-10060
z, м	0	0	0	0	0	0	500	400	800	1400	1100	600	300

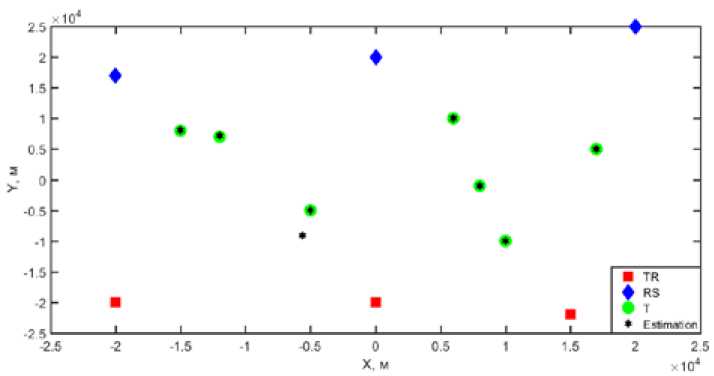
Рис. 3. Геометрия численного эксперимента

Fig. 3. Geometry of numerical experiment

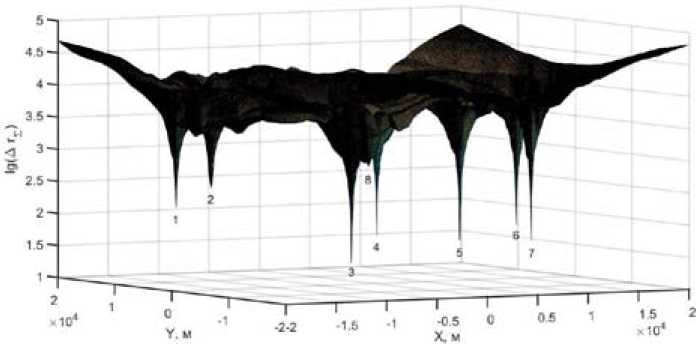
Рис. 4. Пространственное распределение логарифма суммарной невязки

Fig. 4. Spatial allocation of logarithm of total discrepancy of measurements вые семь оценок (хm, уm ) практически полностью совпали с местоположением истинных целей, а восьмая оценка не совпадает ни с одной целью.

Для исключения ложных целей значение функции в проверяемых точках минимума lg ( A r ^ ( х, у ) ) в соответствии с (10) сравнивалось с порогом h , величина которого была рассчитана в соответствии с (6) – (9) и составила значение h = 2.96.

Соотношение между значениями lg (Ar^ (х, у)) для всех восьми проверяемых точек минимума суммарной невязки и значением порога изображено на рис. 5, где по горизонтальной оси отложен номер проверяемой точки по мере возрастания суммарной невязки, а по вертикальной оси отложено само значение невязки. Проверяемые значения lg (Ar (.х, у)) показаны жирными s крестиками, а пороговое значение h – горизонтальной линией. Видно, что первые семь точек минимума суммарной невязки удовлетворяют критерию (10) и соответствующие координаты – 715 –

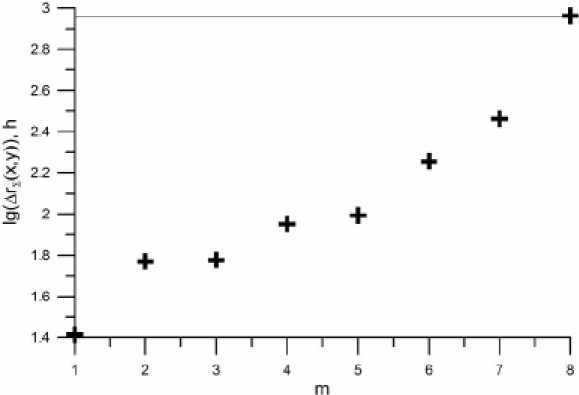
Рис. 5. Соотношение между lg ( A r ^ ( x,y ) ) для восьми точек минимума суммарной невязки и значением порога h

Fig. 5. Ratio between lg (ar (x,y)) for eight points of a minimum of total discrepancy of measurements and value of threshold h x, y) могут быть выбраны в качестве грубой оценки координат наблюдаемых целей (x У )

Для восьмой точки значение lg ( A r ( x , y ) ) превысило величину порога, и, следовательно, эта точка была определена как ложная цель.

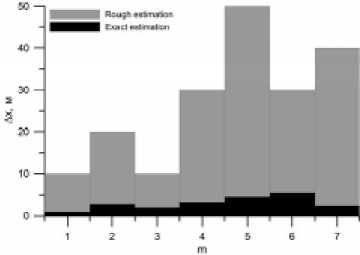
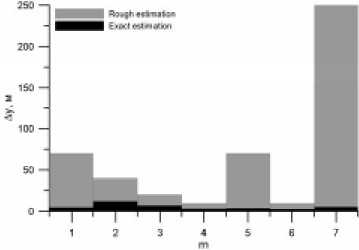
Степень отклонения A x m , ^{A y} m полученных грубых оценок ⁽ x m , ^y _m ) от истинных координат цели ( x m , y m , z m ) представлена на рис. 6 a , 6 b серыми диаграммами, где по горизонтальной оси отложен номер цели. Видно, что по координате x ошибка не превышает половины шага виртуального обзора по соответствующей координате, по оси y ошибка значительно больше и достигает 250 м.

На рис. 6 c ошибка грубой оценки по координате z представлена как модуль разности между истинной высотой цели z m и серединой зоны действия МПРЛС по высоте z и достигает значений 900 м.

Эффективность межпозиционного отождествления измерений и правильность формирования векторов измерений R _m была оценена по точности определения координат целей ( x * ,y m , z * ) итерационным суммарно-дальномерным методом наименьших квадратов [10], для которого сформированные векторы R _m были использованы в качестве измерений для каждой m -й цели, а грубые оценки координат целей ( x_m , y_m , z ) применены в качестве начального решения координатной задачи.

Степень отклонения A x * , A y * _m , A z * полученной точной оценки ( x m , y m , z* _m ) от заданных координат ( x_m , y_m , z_m ) целей показана на рис. 6 в виде черных диаграмм. Видно, что ошибки точной оценки по координатам x (рис. 6 a ) и y (рис. 6 b ) сократились на порядок относительно A x_m , A y_m и составляют единицы метров. Погрешность точной оценки по координате z (рис. 6 с ) сократилась, но не так значительно (примерно в 6 раз) и не превышает значения 150 м, что мо-

b )

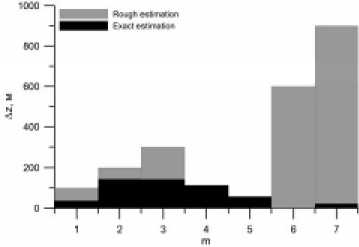
Рис. 6. Степень отклонения грубых (серые диаграммы) и точных (черные диаграммы) оценок координат целей от их истинных значений: a – по координате x ; b – по координате y ; c – по координате z

Fig. 6. Level of a deviation rough (gray charts) and exact (black charts) estimations of coordinates of the targets from their true values: a – on coordinate x; b – on coordinate y; c – on coordinate z жет быть объяснено конфигурацией МПРЛС и погрешностью дальномерных измерений. Высо- кая точность полученных оценок

( *    *

x_m ^*, y_m ^*

zm )

координат целей свидетельствует о правильном

определении принадлежности полученных в разных позициях измерений тем или иным целям и правильном формировании векторов измерений для каждой цели.

Заключение

Таким образом, в настоящей статье предложен новый способ межпозиционного отождествления измерений и предварительного определения координат воздушных целей в суммарнодальномерной МПРЛС в условиях многоцелевой обстановки, когда завязка траекторий целей еще не произошла и все цели наблюдаются одновременно. Способ основан на виртуальном обзоре пространства, использует только суммарно-дальномерные измерения и не требует измерения дополнительных параметров. Результаты, полученные в ходе численного имитационного моделирования, показывают высокую степень эффективности предложенного способа как по точности получаемой предварительной оценки координат целей, так и по правильности формирования векторов измерений для каждой наблюдаемой цели.