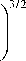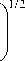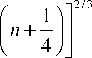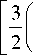МГД-резонатор в лобовой части магнитосферы и его возбуждение внемагнитосферными гидромагнитными волнами (монохроматические колебания)

Проникновение гидромагнитных волн из солнечного ветра в магнитосферу является одним из основных механизмов возбуждения в ней гидромаг-нитных колебаний. Достаточно сказать, что геомагнитные пульсации Рс3, практически постоянно существующие в дневной полусфере, энергия которых превосходит энергию всех остальных пульсаций вместе взятых [Гульельми, Троицкая, 1973], возбуждаются именно таким механизмом [Guglielmi, 1974; Гульелми и др., 1976; Potapov, Mazur, 1984]. К этому же классу можно отнести и пульсации, возникающие в результате событий SC (sudden commencement) [Baumjohann, et al., 1984; Lysak, Lee, 1992; Fujita, Tanaka, 2006].

В теоретических работах, посвященных такому механизму, основное внимание уделяется возбуждению проникающей в магнитосферу волной альф-веновского резонанса [Kivelson, Southwood, 1986; Mann, et al., 1995; Walker, 2002]. Но в этих работах не учитывается тот факт, что магнитосфера может обладать свойствами МГД-резонатора. Между тем, возможность того, что роль резонатора может играть как магнитосфера в целом, так и различные ее области, давно обсуждается в литературе [Kivelson, Southwood, 1985; Walker, 1998; Leonovich, Mazur, 2006]. Совершенно ясно, что наличие в магнитосфере МГД-резонатора должно решающим образом влиять на эффективность проникновения в нее гид-ромагнитных волн, амплитуду колебаний в ней и уровень возбуждения альфвеновского резонанса. Настоящая работа посвящена теоретическому исследованию этого круга вопросов.

Мы ограничиваемся рассмотрением лобовой части магнитосферы и прилегающей к ней области сол- нечного ветра (magnetosheath). Представляется, что наиболее естественно падение гидромагнитных волн из солнечного ветра именно на лобовую часть магнитосферы. Кроме того, к лобовой части магнитосферы примыкает застойная область солнечного ветра, поэтому исследование не осложняется сдвиговым течением на магнитопаузе, не проявляется неустойчивость Кельвина–Гельмгольца, столь важная на флангах магнитосферы.

Для описания указанных областей магнитосферы и солнечного ветра мы используем одномернонеоднородную модель среды, в которой учитывается только радиальная неоднородность. Именно эта неоднородность приводит к запиранию МГД-волны между магнитопаузой и точкой поворота в глубине магнитосферы.

В настоящей статье излагаются результаты первой части работы, посвященной монохроматическим колебаниям (т. е. колебаниям с фиксированной частотой). Результаты такого исследования представляют самостоятельный интерес, кроме того, они являются основой для изучения нестационарных и стохастических колебаний, которым посвящены вторая и третья части работы, публикуемые в этом же номере, непосредственно за настоящей статьей.

Модель среды

Схематическое изображение лобовой части магнитосферы и прилегающей к ней части солнечного ветра, а также используемая нами одномерная модель этих областей представлены на рис. 1. Из этого рисунка видно соответствие между различными элементами модели и реальной системы.

Координата x декартовой системы координат, направленная вдоль неоднородности, меняется в модели

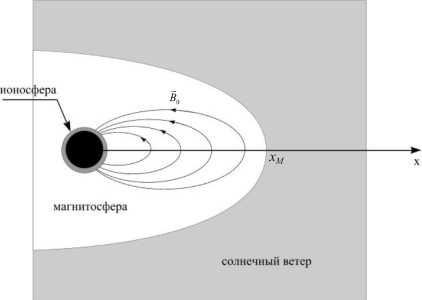
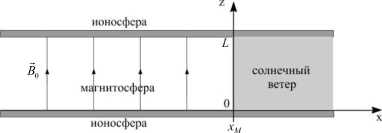
Рис . 1. Соответствие между элементами реальной сре ды и ее одномерной модели .

в пределах (–∞, ∞). Точка x = x M соответствует магнитопаузе. По оси z плазма в модели ограничена проводящими плоскостями z =0, L , изображающими магнитосопряженные области ионосферы. Чтобы сохранить одномерный характер модели, мы примиряемся с наличием этих плоскостей и в области солнечного ветра x > x M . Ось y моделирует азимутальную координату магнитосферы.

Магнитное поле B 0 = B ₀ ( x ) будем считать направленным по оси z как в магнитосфере, так и в солнечном ветре. Впрочем, как будет видно ниже, направление магнитного поля в солнечном ветре не играет большой роли.

На рис. 2 представлены схематические графики зависимостей от x существенных для нашей задачи параметров среды. Отметим, что в солнечном ветре для нас будет важен только тот факт, что c _S >>  c A , конкретные же зависимости c S ( x ) и c A ( x ) в этой области существенного значения не имеют.

Для оценок по порядку величины примем следующие значения: L =1.5·10⁵ км (что соответствует силовой линии геомагнитного поля, экваториальный радиус которой равен a =7 R E =5·10⁴ км), с AM =10³ км/с, с _SW=2·10² км/с, с _AW=50 км/с. В развиваемой ниже тео-

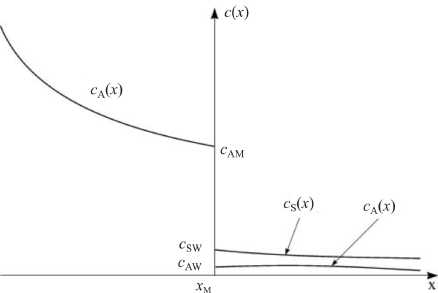
Рис . 2. Схематические графики скорости Альфвена с _A( x ) и скорости звука c _S( x ) в магнитосфере и солнечном ветре .

рии отношение сSW/cAM будет считаться малым параметром. Оно связано с большим скачком плотности на магнитопаузе. Из условия равновесия нетрудно получить, что cSW /cAM ~ (ρM /ρW ) .                           (1)

Исходные уравнения

Пространственно-временную зависимость возмущенной величины ξ _x , проекции вектора смещения плазмы ξ, представим в виде

^ x ( x , y , z , t ) = § x ( x ) U n ( z ) e ik y y "  ” ^t ) .                  (2)

Здесь

U N ( z) = sin k_zz , k_z = k N = n N / L ,              (3)

где N =1, 2, 3, … – продольное (вдоль магнитного поля) волновое число. Зависимость от z вида (3) следует из граничного условия

• § x I z =0, L = 0,

которое в приближении идеальной гидродинамики вытекает из предполагаемой нами идеальной проводимости ионосферных плоскостей. Учитывая циклический характер азимутальной координаты y в реальной магнитосфере, будем считать, что k y = m / a , где m =0, 1, 2, … – азимутальное волновое число, a – характерное значение экваториального радиуса, отвечающего силовой линии длины L . Таким образом, решение (2) определяется волновыми числами m и N . При исследовании возбуждения магнитосферных колебаний внемагнитосферными волнами наибольшее значение имеют гармоники с наименьшими значениями N , поскольку они более эффективно возбуждаются внешней волной. Поэтому для оценок мы будем считать, что N =1. Для азимутального волнового числа будем считать характерными значения m =3÷5. Меньшие значения m неоправданны из-за реально существующей азимутальной асимметрии магнитосферы и еще более из-за азимутальной асимметрии падающей волны, а для больших значений резко уменьшается эффективность возбуждения.

Предполагая применимость приближения идеальной гидродинамики, можно получить уравнение , описывающее структуру колебания по координате x [Du-hau, Gratton, 1975]:

d_ p 0 Q A d^ x dx K2 dx

+ p 0 Q A § x = 0.

Здесь ρ 0 =ρ 0 ( x ) – плотность плазмы,

Q A = ю²

— k ? c A ,

ω4

K ²

2  2   2    222

to ( c A + C s ) — k_z c A C s

^{— k}t ,

kt² = k y + k ².

В дальнейшем мы предпочтем вместо уравнения (4) для ξ x использовать уравнение для функции

• 2     %

5( x ) = — ^Pl 0 ^Q A d ^ x ,                              (5)

K 2 dx которое имеет вид d2% _ d ln Po^A di + K2- _ o. dx2 dx dx

Некоторое преимущество этого уравнения состоит в том, что в нем эффекты альфвеновского резонанса и точек поворота описываются разными членами.

Через функцию ς можно выразить все другие

где величина {f}  означает скачок величины f в xM точке xM. Из формул (7) и (11) видно, что условия (12) означают непрерывность на магнитопаузе смещения плазмы ξx и полного возмущенного давления P.

Общее выражение для закона сохранения энергии МГД-волн имеет вид [Ландау, Лифшиц, 1982]

возмущенные величины. Для компонент вектора смещения ξ имеем

dW r

---+ div 5 + Q _ o. dt

1    d i = _ ik y %

P o ^ A dx ’ y   P o ^ A ^?

Здесь

W

Компоненты возмущенных электрического E и магнитного B полей более простым образом выражаются через компоненты вектора смещения ξ , но

B ² + P o v² + p P 8π 2 2ρ₀

, ^ r _ T" [ EE B ] 4n ^{L   J}

r + pv

при необходимости, используя соотношения (7), их можно выразить и через i. Имеем (далее для крат-

– плотность энергии и плотность потока энергии волны, Q – плотность диссипируемой мощности, а

•r - возмущенная скорость плазмы. В рассматриваемом одномерном случае уравнение (13) принимает вид

i ( ky - to t ) x кости опускаем множитель e ^y )

Ex _ E x ( x ) U n ( z ),

E x _ i ^ S

%.

c

y ,   E y

Ey _ Ey (x) Un (z), Ez _ 0, toBo %                         (8)

^_ i ^S x .

c

d W д 5 - _п --+ — + Q _ o, д t д x

Компоненты B x и B y имеют другую зависимость от координаты z , описываемую функцией V n ( z ) _ cos k_zz :

B x _ B x ( x ) V n ( z ), B y _

_ В (x) VN (z), B _ B (x) UN (z), y N       z z      N                       (9)

B x _ k z B 0 S x , B y _ k z B o S y ,

B z __ ( B o S x ) ‘_ ik y B o S y .

Для возмущенного давления p _ p(x) Un (z), p _

‘ %             to² c _S²          %                   (Ю)

p o ^S x ⁺    2/ 2 .   2 ,    , 2 2 2 ^{i .}

^{to (} c S ⁺ c A ) — ^kz c S c A

где черта над буквой означает усреднение по координате z и по фазе φ= k y y –ω t (последнее равносильно усреднению по координате y или по времени t ).

Использование комплексной записи для возмущенных величин F = fe^{i φ} , где f = f 1 + if 2 , подразумевает, что в действительности F =Re fe^{i φ} = f 1 cos φ– f 2 sin φ. Поэтому для усредненных билинейных комбинаций имеем (FG) ^ (Re F • Re G ) _ (1/ 2)( f . g 1 + f _г g 2 ) _ (1/4) X x ( fg * + f * g ). Усреднение по z функций U_j( ( z ) и V_N ²( z ) дает множитель 1/2, а среднее от произведения U_N ( z ) V_N ( z ) равно нулю.

Учитывая сказанное, имеем

—

W _ 1 i B |i + P^+ p ^P-

4 8n       2          4p„

V                               2

Наконец, для полного возмущенного давления:

P _ p + B i B ^ _ i( x ) U n ( z ).

4π

Из последнего соотношения ясен физический смысл используемой нами функции i( x ).

Граничное условие для уравнения (6) при x →–∞, где имеет место область непрозрачности, сводится к требованию ограниченности решения, что фактически приводит к его экспоненциальному падению. При x →∞ в области прозрачности (распространения волны) граничное условие зависит от постановки задачи. В задаче о собственных модах резонатора таким условием является требование убегания волны, а в задаче о падении волны на магнитосферу задается амплитуда падающей волны.

На магнитопаузе, при x = x M , коэффициенты уравнения (6) испытывают скачки. Из этого уравнения следуют условия сшивки

S_x _ — ( E y B z + E y B z ) + i 7( p S x _ p S x ).     (16)

32π                8

Что касается диссипируемой мощности, то в рамках приближения идеальной МГД она равна нулю. Однако в точке альфвеновского резонанса диссипацией нельзя пренебрегать в принципе – она остается конечной даже при стремлении диссипативных коэффициентов к нулю. Подробнее этот вопрос рассмотрен ниже, где и приведена формула для Q .

Используя соотношения (7–10), выражение (16) можно привести к виду

ω

5t _ i-----r x 8Po^A

d %*, dd i )

i _ i I ■ dx dx )

Аналогичное выражение для W слишком громоздко, и мы приведем его в следующем разделе только для магнитосферной части модели, где оно значительно упрощается.

{i}  _ o, J      dln^ r  _ o, xM     1 Po^A dx £ xM

Приближение ВКБ

Аналитическое решение основного уравнения (6) в общем случае, конечно, невозможно. Поэтому для его решения будем использовать приближение ВКБ.

Как будет видно ниже, для интересующих нас колебаний это приближение, безусловно, выполняется в области солнечного ветра, x > x _M. В магнитосферной области, x < x M , оно выполняется для высоких гармоник магнитосферного резонатора, но находится на границе своей применимости для наиболее важных первых гармоник. Однако приближение ВКБ обладает замечательным свойством – оно дает качественно правильные результаты даже на границе своей применимости. Поскольку характер используемой нами модели среды позволяет рассчитывать только на результаты качественного характера, мы без колебаний будем использовать формулы приближения ВКБ.

Согласно методу ВКБ решение ищется в виде <%( x ) = exp[ i Ф ( x )]. Для применимости метода необходимо, чтобы фаза Ф ( x ) быстро менялась, т. е. чтобы большим был параметр

5 = l I d Ф / dx 1 >> 1, (18)

Решения (20) могут быть написаны для каждой из областей, в которых применимо приближение ВКБ, причем с различными значениями констант C_i . В разделяющих эти области окрестностях особых точек основное уравнение (6) приводится к определенным стандартным формам, решение которых хорошо известно. После этого методом сращивания асимптотических разложений получают единое решение для всех x .

Решение (20) в области прозрачности можно трактовать как суперпозицию падающей и отраженной волн. Запишем его следующим образом:

^( x ) = C 0

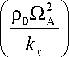
X

x

— i J k_x ( x ‘ ) dx'

x _R

х < exp

+ R exp

x i J kx(x‘) dx' -.

. ^x R                 J

где l – характерный масштаб изменения коэффициентов уравнения. Решение для фазы ищется в виде асимптотического разложения по степеням 1/ S :

Ф ( x ) = Ф ₀( x ) + Ф 1 ( x ) + ...                      (19)

Два первых члена разложения имеют вид

Ф ₀ ( x ) = ± J k_x ( x ) dx , k x ( x ) = K ² ( x ),

Величину R будем называть комплексным коэффициентом отражения. Для решений (20) и (23) плотность потока энергии (17) принимает простой вид:

5 = -_ю( — I C I² + 1 C I²) = — _юI C I² (1 — I R I²у (24) x ₄           0         1          ₄       0

Решение для магнитосферы В этой области c S =0, поэтому

Ф. ( x ) = - i In C + — i In 1 ₂

k_x ( x )

P o ( x №A ( x )

где C – произвольная постоянная. С учетом этих двух порядков общее решение представляется в виде

%( x ) =

p o ^ A ²

kx

|^ C 0 exp ( — i J k x dx ) + C 1 exp ( i J k x dx ) ] .

Неравенство (18) при подстановке в него нулевого приближения (19) дает условие

I k x I 1 >>  1.                                             (21)

Оно означает, что длина волны возмущения 1/ k_x должна быть много меньше масштаба неоднородности. Однако это условие необходимо, но недостаточно. Полная формулировка условия применимости приближения ВКБ имеет вид I Ф 0 ( x ) I >> I Ф‘ I. Отсюда вытекают два неравенства:

I k I³ >> Idk 7 dx I, I k Q 2 I >> I d Q 2 / dx I. (22) x          x            x A          A

Эти условия очевидным образом нарушаются в некоторых окрестностях точки поворота x R , в которой k_x(x R ) = 0 , и точки альфвеновского резонанса x _A, в которой Q A ( x A ) = 0. Вдали от этих особых точек для производной применима оценка d/dx ~1/ l , и тогда оба неравенства (22) сводятся к условию (21). Нетрудно убедиться, что выполнение условия (21) вдали от особых точек обеспечивает тот факт, что размеры окрестностей этих точек, в которых приближение ВКБ неприменимо, малы по сравнению с масштабом неоднородности. Конкретные оценки размеров этих окрестностей будут даны ниже.

P 0 Q A

K ²

B ₂₂

= t" q , q 4π

_ω 2     ₂

—— kt = q cA

2 ω ²    2

—^— k., c _A

k y ².

Учитывая также, что B 0 = const , основное уравнение (6) приводим к виду

_— (q ;2)_ _ ,₊ ( q ² — k^ = 0.                     (26)

q

Применяя к уравнению (26) приближение ВКБ, имеем

kx2( x) = q 2( x) — k2 =       — kt2, cA2 (x)

где обозначено kt² = k ^ + k . 2 . Так как мы предполагаем, что функция c A ( x ) монотонно падает на интервале (–∞, x _M), то уравнение для точки поворота k x ( x R ) = 0 имеет в этом интервале решение, если

® >  ^kt c AM -

При этом интервал (–∞, x R ) – это область непрозрачности ( kx’ <  0), а интервал ( x _R, x _M) - область

прозрачности ( k x >  0). Для существования собственных мод в магнитосфере необходимо наличие в ней области прозрачности, поэтому мы будем предполагать выполнение условия (27). Точка альфве-

новского резонанса определяется уравнением q ²( x A )=0. Она лежит в области непрозрачности левее точки поворота: x A < x R .

Вблизи этих точек будем использовать разложения

ω c A( x) = — kz

1 —

x — x _A I , _ to ----A , c _A ( x ) = —

2 1 A J A        k t

1 —

x —

x _R

2 l R

. (28)

Далее будем считать, что l _A~ l _R~ l – величины одного порядка. Используя (28), условия применимости приближения ВКБ (22) можно привести к виду

I x - x . I >>A. = 1/ к ,I x - x _R I >> A_R = (L / k 2 )^1/3.(29) A A y R R R t

Размеры окрестностей особых точек, в которых неприменимо приближение ВКБ ΔA и ΔR, малы по сравнению с соответствующими масштабами неоднородности lA и lR, если kyl >> 1. (30)

Условие (30) можно считать конкретизацией общего соотношения (23) на области, удовлетворяющие неравенствам (29). В реальной магнитосфере, с учетом того, что ky=m/a и l~a, где a – характерный радиус магнитной оболочки, на которой рассматривается возмущение, неравенство (30) сводится к условию m >> 1. (31)

Напомним, что мы считаем характерными значения m =3÷5, так что с некоторой натяжкой условие (31) можно считать выполненным.

При выполнении условия (30), (31) магнитосферная область x < x M разбивается на пять интервалов: три интервала, в которых применимо приближение ВКБ, лежащих в областях x < x A , x A < x < x R , x > x R , и две окрестности особых точек - I x - x A I A и I x - x _R I _R. В первых трех интервалах можно написать соответствующие выражения приближения ВКБ. В разделяющих их окрестностях особых точек, используя разложения (28), основное уравнение (26) можно упростить и привести к определенным стандартным формам: вблизи точки x A – к уравнению Бесселя, а вблизи точки x R – к уравнению Эйри, для которых также можно написать соответствующие решения. После этого, учитывая граничное условие при x →–∞ и используя метод сращивания асимптотических разложений, можно все произвольные константы, задающие решения в разных интервалах, выразить через одну константу – амплитуду волны в магнитосфере. Не приводя детали достаточно очевидных выкладок, кратко опишем получающееся таким образом решение.

В первой области применимости приближения ВКБ x < x A , I x - x A I >>A A ,

нологически оно сводится к замене в выражении (25) для q ² величины ω на ω+ i γ, где γ>0 – бесконечно малая. Это приводит к сдвигу особой точки в нижнюю полуплоскость: x A → x A – i ε, где ε=2γ/ω, т. е. к обходу ее сверху. При таком обходе из (33) получается (34).

При I x - x A I << A A два главных члена разложения выражений (33) и (34) совпадают:

^{S ( x} ) = S A

1 +

( x - x A )² 2 A A

x - xA

Функция S( x ) в точке x = x A конечна: S( x A ) = s A ■ Но из соотношений (7)–(9) видно, что величины ξ _y , E_x , B_y имеют особенность вида ( x – x A )^–1, а величины ξ _x , E_y , B_x – особенность вида ln( x – x A ).

В области применимости метода ВКБ между точками x A и x _R, т. е. при x - x A >> A A , x _R - x >> A R ,

%( x ) = - iC

q ² ( x ) k_x ( x )

1/2 I x I exp J I kx (x') dx‘ .

U J

Это выражение представляет собой растущую экспоненту. Удерживать на ее фоне падающую экспоненту, т. е. второе линейно независимое решение в выражении (20), не позволяет точность метода ВКБ. Выражение (36) можно переписать в виде:

S( x ) = C M

q ²( x ) k_x ( x )

exp

J I k x ( x ') I dx'

V x R               J

S( x ) = C

q ² ( x ) k_x ( x )

^1/2 i x

exp j I k x ( x ‘ ) I dx' .

V ^x A

Вблизи точки

I x - x A I << l A ,

альфвеновского резонанса, при

I x - x I I x - x I

%( x ) = S A I —;— I K 1I —;— I при x < x A ,      (33)

V ^A A J V ^A A J

^{S ( x} ) = S A

x - xA

A

A

x > x _A.

K 1

x -

x _A

A

A

—i п 1 1

^{x - x} A

A

A

при

Здесь K 1 (ξ) и I 1 (ξ) – модифицированные функции Бесселя [Справочник по специальным функциям, 1979]. Точка x= x A есть точка ветвления решения (33), (34). Правило ее обхода хорошо известно [Ландау, 1949; Линь, 1958;Арцимович, Сагдеев, 1979]. Феноме-

где

^C M = ^{- iC} exp ^r AR

xR rAR = j I kx (x) I dx.

x _A

Экспоненциальный множитель exp Г_AR характеризует возрастание амплитуды колебания от точки x _A до точки x _R. Фактор Г_AR при выполнении условия (30) велик: Г AR >>1. Интеграл (39) можно вычислить аналитически, если предположить, что второе из выражений (28) справедливо вплоть до точки x = x A : k ²

Г ar = 3( k y A r )³ = - k^ k y l r .                  (40)

В общем случае это выражение можно использовать как оценку по порядку величины.

Вблизи точки поворота, при I x - x _R I <<  l _R,

I x _R - x ¹ S ^{( x} ) = S r Ai I          I .

V ^A R J

Здесь Ai (η) – функция Эйри [Справочник по специальным функциям, 1979]. Точка поворота x = x _R, будучи особой точкой асимптотического разложения ВКБ, не является особой для самого уравнения (26). Поэтому решение (41) аналитично в точке x R .

Наконец, в области прозрачности x > x R и при условии применимости приближения ВКБ x – x R >>Δ R имеем

S( x ) = 2 C M

1/2 q ( x )

k_x ( x )

cos

^ ( x ) - ^п 4

Здесь выражение для фазы Ψ( x ) конкретизировано следующим образом:

K ( x ) = j k x ( x ‘ ) dx '.                              (43)

x _R

Все константы, определяющие амплитуду колебания в различных областях, можно выразить через одну – любую из них. Выразим их через C M – амплитуду в области прозрачности. Выражение для C следует из (38). Для констант ς_A и ς_R имеем

S a = 4 F У ^P' I .' ^C m ,                (44)

π k_yl _A ^1/2

S r = 2 7П k y AR^{/ 2} C m .                             (45)

Из приведенных выражений ясно видно, что рассматриваемое колебание в области прозрачности представляет собой быстрый магнитный звук (БМЗ) с дисперсионным уравнением

2    22    2    2    2    2

to — ca k , k — kx + ky + kz, а в точке альфвеновского резонанса – альфвенов-скую волну с дисперсионным уравнением

2   22

to — c A k z .

Фаза приближения ВКБ (43) зависит как от параметра от частоты колебания: Ψ=Ψ( x , ω). Важную роль в дальнейшем изложении будет играть значение фазы в точке x = x M , которое является функцией одной только частоты:

x _M       2

К _M(to) ^( x M , to) — J .k— - k² dx.      (46)

x R ( ω ) ^c A ^{2 ( x )}

Подчеркнем, что нижний предел в этом интеграле также является функцией частоты: x R = x R (ω).

Производная τg=dΨM(ω)/dω есть время пробега с групповой скоростью волны частотой ω от точки поворота до магнитопаузы. Действительно, d xM                xM

Tg (to) — —    kx (x, to) dx —    —-----, dω                      v (x, ω)

xR (ω)                      xR (ω) g , где

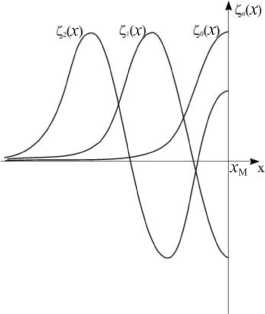
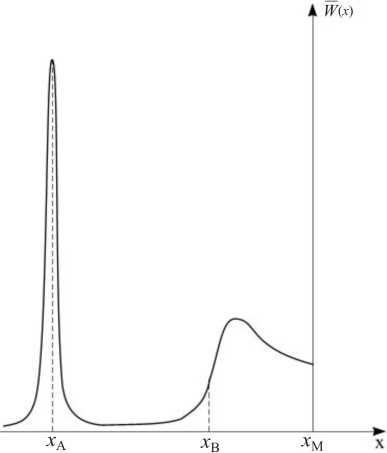
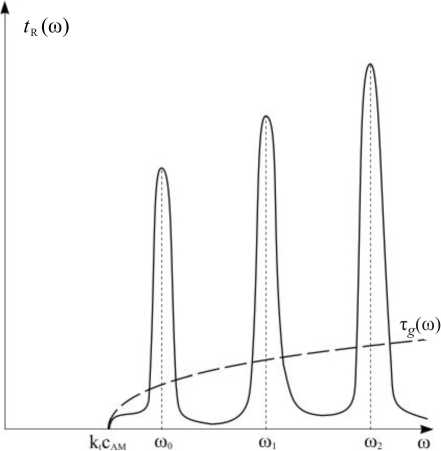
( dk V k c2 k x          x A g   (dto J       to k есть проекция полной групповой скорости быстрого магнитного звука cA на ось x.

Функции (46) и (47) определены только для to2 > k2cAM. Их легко вычислить, если to2-kt2x ×c2AM<

x-

_

x_M

2lM

справедливое при xM–x<<lM. Будем считать, что величина lM того же порядка, что lA и lM, т. е. порядка l. Имеем

К M(to) — 3 k,l m

^to2 ^{- k}t^cAm _kt2_cA2_M

Tg (to) — 2 -^ ^cAM

2   22

to   kt cAM t cAM

Плотность энергии колебаний (15) в магнитосферной области x<x_M можно привести к виду

W —

2B0²

q⁴+k²(^k2+^k"),%k²+kz %‘

4             | S | +       4

q4

. (50)

В области прозрачности, подставляя решение (42), получаем отсюда

W—|n CMp

B₀

X

q4+k2(k2+k2)

2cos kxq

+ k-(k’ ⁺k² ) sin2 [„x) q -

П к x)^- - ₊

π

Усредним это выражение по мелкомасштабным пространственным осцилляциям, длина волны которых порядка 1/kx<<l. Сохраняя для такого среднего прежнее обозначение, имеем

2πω C²

W (x) —---- ^M.

B₀²     v_g(x, ω)

Полная энергия, заключенная в области прозрачности, дается выражением xM           2πωτ (ω) C 2

W — J W(x) dx —-----g 1 M| xR                    B0

.

В дальнейшем изложении важную роль будут играть решения в магнитосфере, удовлетворяющие граничному условию на магнитопаузе d^ L — 0. dx xM

Оно равносильно условию ^_x I_xm — 0, означающему, что нормальное к магнитопаузе смещение плазмы равно нулю. Ниже мы увидим, что в задаче о собственных колебаниях магнитосферы это условие является нулевым приближением по малому параметру c_SW/c_AM для условий сшивки на магнитопаузе. Поэтому соответствующие решения будем называть собственными модами.

Подстановка в (53) решения (42) дает условие к M(to) — n( n +1/4),                            (54)

где n — 0, 1, 2,... - волновое число по координате x. Уравнение (54) вполне аналогично условию Бора– Зоммерфельда в квантовой механике, оно определяет собственные частоты резонатора to — ton. Если в нем использовать выражение для фазы (49), то to n   k,c AM

1 +1

1 (ktlM)^2/3

Это выражение применимо, если n<<ktlM (тогда размер локализации моды по оси x мал по сравнению с lM, и на этом размере применимо разложение (48)). С другой стороны, приближение ВКБ требует n>>1. Эти условия совместимы, поскольку ktlM>>1.

Описанное выше решение ς%(x) также зависит от го как от параметра, т. е. % = %(x, to). При to=to_n это решение представляет собой собственную функцию:

%n = %n⁽x) = %⁽x, ^ton )•

Для значений n<<ktlM, когда мода локализована на размере, много меньшем lM, для нее можно использовать выражение (41) во всей области прозрачности. Действительно, в этом случае можно считать, что разложения (28) в точке поворота и (48) на магнитопаузе совпадают, так что lR=lM и

I to xR — xR (to) xM 21M I 7        1

I kc AM

Если подставить эти выражения в (41), то при ω=ωn получаем

I x — x 1

% n^(x) = % R ^Ai\ ~ П n⁺ —  I.                    ⁽⁵⁶⁾

I       ^AR )

Здесь nn - нули функции Ai ‘(—n), т. е. Ai‘(—П_n) = 0. Нули Пn (n=0, 1, 2, —) представляют собой возрастающую последовательность положительных чисел, характерное значение которых порядка единицы. При n>>1

η_n

n + —

2/3

Собственные частоты выражаются через эти числа:

^ton = kc AM

1 + ^{1   П}n

²(kJm )^1/3

При n>>1 выражение (57) для частоты переходит в (55), а выражение (56) для собственной функции в области прозрачности – в (42). Подчеркнем, что в практическом плане важны моды с n~1, которые описываются выражениями (56) и (57). Графики первых трех собственных мод ςn(x) изображены на рис. 3.

Рис. 3. Графики собственных функций магнитосферного резонатора ς_n(x).

Вблизи частоты ω=ωn функцию ΨM(ω) можно представить в виде

T M (to) = n( n +1/4) + (to — ton) т gn, где тgn = тg (ton). Из этой формулы видно, что характерное расстояние между соседними собственными частотами равно τgn1 .

Поглощение в окрестности альфвеновского резонанса

Общее решение в области прозрачности (23) для магнитосферы можно записать в виде iп/4 q (x)

%(x) = СM e  ——х

L kx (x) J

x{exp [—i T (x) ] + Rm exp [ i T (x) ]}.

Сравнение с полученным выше решением (42) дает для коэффициента отражения значение R_M= e"i^п/2. Его модуль R_M| = 1, т. е. потоки энергии падающей на точку отражения и отраженной от нее волн равны. Это означает, что эффект поглощения энергии в окрестности альфвеновского резонанса в решении (42) утерян. Причина этого заключается в отмеченном выше обстоятельстве – точность метода ВКБ не позволяет определить в интервале (xA, xR) падающую экспоненту на фоне растущей. В результате при переходе в область x>x_R теряется экспоненциально малый эффект поглощения.

Учтем его следующим образом. Используя найденное решение, в частности связь между %(x_A) = %_A и CM как нулевое приближение, вычислим мощность, диссипируемую в окрестности альфвеновского резонанса. После этого с помощью уравнения сохранения энергии (14) найдем поправку к коэффициенту отражения R_M.

Вблизи точки альфвеновского резонанса выражение для плотности энергии (50) принимает вид

W (x) =

π ky²kz²

B0²q⁴ (x)

Это выражение в точке x=xA обращается в бесконечность. Для его регуляризации необходимо учесть эффекты, выходящие за рамки идеальной МГД.

В условиях земной магнитосферы важнейшим из таких эффектов является затухание колебаний в ионосфере, обусловленное ее конечной проводимостью. Вблизи точки x_A колебание представляет собой альфвеновскую волну. Декремент затухания альфвеновских волн в ионосфере вычислялся во многих работах [Newton, et al., 1978; Southwood, Hughes, 1983]. Применительно к нашей модели среды такой расчет дан в приложении. В дальнейшем для нас будет важен только тот факт, что этот декремент γA много меньше частоты волны ω. Характерные значения для стоячих альфвеновских волн в магнитосфере γA/ω~10^–1÷10^–3 [Newton, et al., 1978].

Согласно результатам приложения, конечная проводимость ионосферы приводит в уравнении (26) к замене q²^ <%²= q²+ ik^8_P, что равносильно замене to ^ to + iyA, где 8_P связано с ya соотношением

ε_P=2γ_A/ω. Такая замена согласуется с использованным выше правилом обхода особой точки. Вблизи точки x=x_A, там, где применимо разложение (28), имеем

2 = k 2 x — xA + iSP 1A q z I

A

.

Для комплексных значений q² множитель q⁴=(q²)² в знаменателе выражения (59) заменяется на q^{2 2} . Таким образом,

W (x) =

ПкЖ,  ,2 =     4 8a 1A |Cm|²

B02 |q²|² ^     B02 [(x-xa)² + SP1A].

Здесь использовано соотношение (44) и введен малый параметр

8a = (1/2) exp (-2rAR),

iφM

M 'Me .

Для модуля получаем

Tm = 1 — 28a.

Фаза в нулевом порядке, как мы видели, имеет значение φM=–π/2. В следующем порядке положим фм =— "2 + aM, |ам| << 1.

Примененный нами метод определяет поправку к TM, но не позволяет найти поправку αM. Ниже будет видно, что первая поправка определяет декремент затухания собственной моды, а вторая – малую поправку к вещественной части частоты. Последняя же не представляет существенного интереса.

характеризующий степень проникновения возмущения из области прозрачности в точку альфвеновско-го резонанса через барьер непрозрачности между точками x_R и x_A.

Полная энергия, сосредоточенная в окрестности альфвеновского резонанса,

Решение для солнечного ветра

Для интересующих нас колебаний в магнитосфере имеется область прозрачности. Это означает, что их частота и > ktc_AM. Поскольку в солнечном ветре c_A<< c_AM, c_S<< c_AM, то в этой области выполняются неравенства

M

WA = J W (x) dx =

— M

2πωδA CM²

B0² γA     ^.

ю >> k_tc_A, ю >> kc_A, to >> kz . c^Ac^S .       (63)

4 cA ⁺cs²

Интеграл здесь формально распространен на бесконечные пределы, так как при использовании выражения (60) он фактически набирается в малом интервале шириной порядка ε_Pl_A вблизи точки x=x_A.

Плотность диссипируемой мощности дается выражением

Из них следует, что в солнечном ветре нет точек поворота, точек альфвеновского резонанса и точек резонанса медленного магнитного звука, т. е. приближение ВКБ применимо в этой области везде.

В силу неравенств (63) имеем

, 2 Ю       pO^A        / \     \ kx =      , -V^A = ®p0(x)cs (x), cS2 (x)      kx

Q (x) = 2Ya W (x) =

4ωδA CM²     ε_Pl_A

B0      (x — xA )2 + SP1 A,

x

J k_x (x‘)dx' = toT_S(x).

x_M

а полная диссипируемая мощность – выражением

• - r-           -   4пи8 |C_m I²

QA = J Q (x) dx = 2y AWa =-----A2 M .       (62)

B —r                               0

Замечательная особенность этих выражений состоит в том, что они не зависят от γA и остаются конечными в пределе γA→0.

Для стационарных колебаний с вещественной частотой в уравнении (14), очевидно, dW / dt = 0. Если два оставшиеся члена уравнения проинтегрировать по x от –∞ до некоторого значения x внутри области прозрачности и учесть, что Sx (—r) = 0, то получим

Sx (x) + QA = 0.

Используем для S_x в области прозрачности выражение (24). Сравнивая (23) и (58), с учетом первого из соотношений (25) видим, что |С₀|2 = (4n/B₀2)|C_m|². Вместе с (62) это дает

IR m|² = 1 — 48a.

Представим коэффициент отражения в виде

x

Здесь ts(x) = J xM dxx cs( x')

– время пробега от магнито-

паузы до точки x с локальной скоростью c_S(x). Из приведенных формул видно, что рассматриваемое колебание представляет собой в солнечном ветре быстрый магнитный звук, который в силу неравенства cS>>cA можно считать просто звуком. Из соотношений (63), (64) следует, что kx>>kt, т. е. рассматриваемые волны падают на магнитопаузу почти нормально. Волны, не удовлетворяющие этому условию, полностью отражаются от магнитопаузы, так как магнитосфера является для них областью непрозрачности.

Общее решение приближения ВКБ (23) в солнечном ветре с учетом соотношений (64) можно записать в виде

^(x) = CW [p0

Величину C_W= C₀ V® будем называть амплитудой падающей волны. Поток энергии падающей волны есть

Sw = Cw|²/4.

При использовании этих обозначений формула (24) для полного потока энергии принимает вид

5, =-5w (1 -|R_w|2).

го интереса. Эта поправка далее будет игнорироваться. По этой же причине будем игнорировать малое слагаемое а_м/2 в выражении (69) для Ф_м. С учетом сказанного имеем:

Условия сшивки на магнитопаузе (12) при подстановке в них решения в магнитосфере (58) и решения в солнечном ветре (65) принимают вид

^to= ^ton^{- iV}„ , ^Vn = ^Vwn^{+ V}An , ^Vwn = =⁵w / ^Tgn , ^V An = ⁵A / ^Tgn .

Cme”/4 (e^-i ^m + Rme ^Фм ) =

1/2

( B² 1      1

= ^CW I TZT I л/Г^{(1 + R} W),

V4nto J 5_w

e^-i^Фм

R ei^Фм ^RM^e

e^-i^Фм

+ R ei^{Ф + 1 v}m e

= 5w

I - Rw

I+Rw^.

Физические причины затухания собственных мод становятся особенно ясны при рассмотрении энергетических соотношений. Амплитуда убегающей волны определяется уравнением (66):

1/2

c =41 ^nton I g^1/2c

Cout ^I _п2 I ^uw CM^.

V B 0 J

Здесь обозначено

X    ^pM cAM    ^{to —}kz cAM

• ^Ow = „           / 3           x1/2 ■

• ^pw csw to (to²- kt²cAM)

По порядку величины, согласно соотношению ⁽¹⁾, ⁵w ~ csw / cAM << 1.

Малая величина параметра δW имеет ключевое значение для развиваемой в настоящей работе теории.

Поток ее энергии

₌ К. 12 _ ^4nton^Vwn^Tgn    |2

⁵out 4 Cout|          B2 Cm| .

Собственные моды магнитосферного резонатора

Для собственных мод магнитосферного резонатора граничное условие при x→∞ есть условие убегания, т. е. отсутствие падающей на магнитопаузу волны. Из общей формулы (65) такое решение можно получить с помощью предельного перехода Cw^0 при условии Cw Rw = Cout = const. Здесь Cout – амплитуда убегающей волны. В этом пределе Rw ^ ^ и соотношение (67) приводится к виду tg [Ф M(to) + i (5w + 5 a)] = 0.                     (68)

Здесь

ФM(to) = pM(to) + фм = * M(to) - 4+0^     (69)

В нулевом порядке по малым параметрам δW, δA, αM уравнение (68) сводится к соотношению (54). Это означает, что описанные выше собственные моды действительно в главном порядке по малым параметрам представляют собой собственные колебания магнитосферы. Тот факт, что в этом главном порядке сшивка с решением в солнечном ветре дает условие (53), или, что то же самое, Е I = 0, является x xM вполне естественным. В пределе ρW/ρM→∞ можно считать, что плазма солнечного ветра обладает очень большой (бесконечной) инерцией и поэтому граница с ней неподвижна.

В следующем порядке по указанным малым параметрам уравнение (68) дает

(to - to n)т gn + ~ = - i(5w + 5а ).

Малая величина αM приводит к малой поправке к реальной части частоты, не представляющей особо-

Сопоставляя формулы (52), (62) и (71), с учетом обозначений (70) приходим к естественным с физической точки зрения соотношениям

5out = 2vwn^R, QA = 2vAnWr.

Из них следует, что

^^t^ = -(5out + Qa )    'rW. .

Энергия собственных мод резонатора теряется по двум каналам – убегает в солнечный ветер через не полностью отражающую магнитопаузу и диссипирует в окрестности альфвеновского резонанса.

Возбуждение магнитосферного резонатора падающей волной

Для полного решения задачи о падении на магнитосферу монохроматической волны из солнечного ветра нам осталось определить коэффициент отражения RW и выразить амплитуду волны в магнитосфере CM через амплитуду волны в солнечном ветре CW.

Коэффициент отражения определяется из уравнения (67). В первом порядке по малым параметрам δA и δW имеем

Rw =

tg ФM(to) + i ( 5a - 5w) tg^P (to) + i (5 A + 5w)

.

В соответствии с аргументами предыдущего раздела здесь и далее считаем, что

Ф M(to) = Ф M(to) - i П /4.

Из (72) следует:

R₂ = tg²«РM(to) + ( 5a - 5w )²

^{1 w|}    tg² «P M(to) + ( 5 a + 5w )^2.

Величина

Qw = 5w (1 -IRw|²)

представляет собой поток энергии из солнечного ветра в магнитосферу. Ее можно трактовать как мощность накачки магнитосферного резонатора. Из (73) имеем

Qw = s

W

4δAδW tg2 Ф m(«) + (8 A + 8 W )2.

полной энергии в окрестности альфвеновского резонанса:

Амплитуда волны в резонаторе C_M определяется уравнением (66). Подставляя в него выражение (72), имеем

_{W -}S _____²⁸A ^{8 W 7 Y}A_____

A ^Wtg²Ф M(to) + (8 A + 8 W )²’

cM = iCW

1/2

2                          1/2

B₀             δ_W

( 4nto J  tgP м(_Ю) + i (8 a + 8 w )

и полной мощности, диссипируемой в этой окрестности:

QA - 2y a Wa - SW

Отсюда

4δAδW tg2«ФM(to) + (8A + 8W )2 ■

ICмГ = Cwf

B₀²           δ_W

4яш tg²Ф_М(_Ю) + (8a + 8w )2

Используя это выражение в формулах (51) и (60), получаем выражения для плотности энергии в об-

ласти прозрачности:

W (x) = Sw

2δW             1

tg²ФмИ + (8A + 8W )² vg⁽x,^ю),

и в окрестности альфвеновского резонанса:

W (x) = S w

28A8W /yA      x tg2 Ф mH + (8 A + 8 W )2X

Из соотношений (74) и (78)–(80) следуют равенства

Qw - 2vA Wr - 2y a Wa - QA.                 (81)

Они означают, что мощность, поступающая из солнечного ветра в магнитосферный резонатор, равна мощности, теряемой резонатором в результате просачивания энергии в область альфвеновского резонанса, которая, в свою очередь, равна мощности, диссипируемой в окрестности альфвеновского резонанса. Таким образом, вся энергия, проникающая в резонатор из солнечного ветра, в конечном счете диссипирует в окрестности альфвеновского резонанса. Особо отметим часть соотношения (95)

VAWr -YAWa,                              (82)

x

ε l_{A            .}

n[(x-xa)² + s²1A ]

Схематический график зависимости W от x приведен на рис. 4. Плотность мощности, диссипируемой в окрестности альфвеновского резонанса, дается выражением

Q (x) - 2 y a W (x) -

= ^Sw

^4δA^δW                  ^εP ^lA        _.

tg²ФM (to) + (8A + 8W )^{2 n}[^{(x - x}A ^{)2 + s}P¹A ]

Проинтегрировав выражения (75)–(77) по координате x, получаем выражения для полной энергии магнитосферного резонатора:

устанавливающую связь между полными энергиями, заключенными в резонаторе и в окрестности альф-веновского резонанса.

Все функции, фигурирующие в (81), имеют одинаковые резонансные знаменатели, которые и определяют их главную зависимость от частоты ω. Более слабая зависимость от ω остальных множителей – δA,δW,τg,γA – не играет существенной роли на этом фоне. Это означает, что все они зависят от частоты примерно одинаково. Рассмотрим для примера одну из них – полную энергию резонатора WR . Точнее, мы рассмотрим отношение tr - Wr/ Sw, (83)

WR

- ^S W

2δWτg tg2ФM(to) + (8A + 8W )2

Рис. 4. График плотности энергии колебаний W(x) в маг-

которое не зависит от амплитуды падающей волны и является характеристикой резонатора как такового.

Величина t_R имеет размерность времени. Ее можно трактовать как время, необходимое для того, чтобы падающий поток, если бы он полностью проникал в резонатор, накачал его до необходимого равновесного уровня. Чем больше t_R, тем выше уровень накачки резонатора. Если бы резонатор в магнитосфере отсутствовал (т. е. не было скачка плотности на магнитопаузе, что соответствует значению δ_W~1), то характерным значением для величины t_R было бы время пробега волны по магнитосфере, т. е. t_R~τ_g. Наличие резонатора существенно меняет ситуацию, приводя к сильной зависимости величины tR от частоты ω .

Главное в этой зависимости – наличие острых максимумов на собственных частотах ω=ωn. При | to - ton | << т^-П имеем

tR(to) -

_________^2vWn_________

(to ^-ton^{)2 +}(VA,, ⁺VWn⁾²

нитосфере.

Ширина резонансного пика равна полному декременту затухания собственной моды v_n - vA, + v_Wn.

Высота пика

и узкие минимумы в точках ω=ωn, где tR(®n ) =

^2VWn

(^VAn ^{+ V}Wn )2

RW(ωn)²

^(VAn ^-VWn^{)2 (v}a,, ^+vwn⁾² .

Если ^VAn ^ ^VWn , то tR^(Юn⁾~^{1/ V}n >> ^Tgn . Таким образом, на резонансных частотах наличие резонатора приводит к значительному увеличению уровня возмущения в магнитосфере.

Функция tR(ю) имеет минимумы в точках ю = юn, в которых tg2 Фм(ю) = ^. Легко увидеть, что частоты ωn чередуются с частотами ωn. Обозначим тgn = тg (юn), VWn = 5w / юn, по порядку величины тgn ~ тgn, VWn ~ VWn. Вблизи минимума, при | ю - юn | << fgn, имеем trH = 2VWnт2 [1+(ю - юn )2 тgn ].             (85)

Значение в минимуме tR (юn) = 2vWn тgn много меньше значения в максимуме:

t_R(ω_n) t_R(ω_n)

(^Vn^тgn )2 << 1.

Более того, оно много меньше значения, характерного в отсутствие резонатора: t_R (Ю_n) << т_gn, т. е. существование резонатора в областях между его собственными частотами уменьшает уровень возбуждения магнитосферы.

Из (85) видно, что характерная ширина минимума τ_gn¹ по порядку величины совпадает с расстоянием между собственными частотами. Таким образом, функция tR(ω) представляет собой набор острых максимумов на собственных частотах с широкими минимумами между ними. Ее схематический график изображен на рис. 5.

Величина RW 2 как функция ω, наоборот, имеет широкие максимумы в точках ю = юn, где ее значение близко к единице:

IRw(Ю „ )|2 = 1 - 45 a 5 w,

Рис. 5. График уровня накачки магнитосферного резона- тора tR(ω).

Отметим любопытный случай V_An = V_Wn. Тогда IR_W(ю_n )|2 = 0, т. е. вся падающая на магнитопаузу энергия проникает в магнитосферу, – имеет место своего рода «просветление» магнитопаузы. Впрочем, это утверждение является лишь приближенным. При учете следующих членов разложения по малому параметру δA=δW имеем в этом случае IRw(юn)2 = 5A/4.

Заключение

Основные результаты работы можно сформулировать следующим образом.

• 1.    Представлена одномерно-неоднородная модель лобовой части магнитосферы и прилегающей застойной области солнечного ветра (magnetosheath), в рамках которой решается задача о падении на магнитосферу гидромагнитной волны из солнечного ветра. Одномерная неоднородность модели по оси x отражает неоднородность магнитосферы поперек магнитных оболочек, в том числе и скачок параметров на магнитопаузе. По координате z плазма в модели ограничена проводящими плоскостями, изображающими магнитосопряженные области ионосферы. Ось y моделирует азимутальную координату магнитосферы, ее цикличность учитывается периодическими граничными условиями. Магнитное поле в модели направлено по оси z. Зависимости скорости Альфвена cA и скорости звука cS от координаты x передают их изменение поперек магнитных оболочек в экваториальной плоскости.

• 2.    В рамках описанной модели и в приближении идеальной МГД установлено существование в магнитосфере резонатора для быстрого магнитного звука. По координате x волна запирается между магнитопаузой и точкой поворота во внутренней магнитосфере, по координате z – между проводящими ионосферными плоскостями, по координате y условие периодичности приводит к квантованию волнового вектора ky. В результате собственные моды резонатора определяются тремя волновыми числами – волновым числом n по координате x (оно равно числу узлов собственной моды), азимутальным волновым числом m и продольным (вдоль магнитного поля) волновым числом N. Таким образом, собственные частоты ω=ωnmN. В рамках приближения ВКБ найдены выражения для собственных частот и собственных мод резонатора. Для основной моды n=m=N=1 и приведенных в тексте характерных значений параметров среды имеем f=ω/2π≈ktcAM/2π≈5 мГц. Затухание собственных мод обусловлено двумя причинами: слабым убеганием волны через не полностью отражающую магнитопаузу в солнечный ветер и поглощением в точке альфвеновского резонанса. Малость последнего обусловлена широким барьером непрозрачности между резонатором и точкой альфвеновского резонанса.

• 3.    Проникновение в магнитосферу гидромаг-нитной волны из солнечного ветра и уровень накач-

• ки магнитосферного резонатора носят ярко выраженный резонансный характер. Энергия колебаний в резонаторе, рассматриваемая как функция частоты падающей волны, имеет острые и высокие пики на собственных частотах резонатора. Энергия, локализованная в окрестности альфвеновского резонанса, пропорциональна энергии резонатора: WA = (vAn / ya) WR. Декремент затухания альфвеновских волн γA довольно мал, γA/ω~10–1÷10–3, так что отношение vAn/γA обычно можно считать большим. Это означает, что энергия колебаний внутри магнитосферы, в основном, сосредоточена вблизи точки альфвеновского резонанса на малом пространственном масштабе Δx~(γA/ω)lA. Но роль магнитосферного резонатора и в этом случае велика – его существование определяет резонансную зависимость уровня колебаний от частоты, а его собственные частоты – места расположения точек альфвеновского резонанса: xAn=xA(ωn).

После изложения результатов работы обсудим вопрос, какие из этих результатов можно считать свойствами колебаний в реальной магнитосфере, а какие есть свойства слишком простой модели среды.

Во-первых, обсудим вывод о существовании резонатора. Представляется, что одномерная неоднородность модели правильно описывает эффект запирания волны поперек магнитных оболочек. В направлении вдоль магнитного поля колебания в нашей модели ограничены проводящими ионосферами. В реальной магнитосфере значительное возрастание скорости Альфвена вдоль силовой линии от экватора к ионосфере приводит к тому, что магнитозвуковые волны не достигают ионосферы, а отражаются от точек (поверхности) поворота и в этом направлении. Но этот факт не отменяет запирания колебания вдоль силовой линии и в рамках нашей модели может быть учтен эффективным уменьшением параметра L.

Более неопределенная ситуация с координатой y. Если азимутальная неоднородность магнитосферы такова, что при движении от лобовой точки к флангам скорость Альфвена нарастает, то возможно запирание волны и по азимуту. В нашей модели этот факт можно учесть ограничением волнового числа m > 2п / Аф , где Аф - азимутальный размер резонатора. При Аф~60^120° имеем m > 3 ^ 6. Если же азимутальная неоднородность носит противоположный характер или просто недостаточна для запирания волны, то резонатор представляет собой тороидальную область, охватывающую Землю, что, собственно, и подразумевается в нашей модели. В таком случае возможны меньшие значения m, но реально имеющаяся азимутальная неоднородность делает самые малые значения m=0, 1 вряд ли приемлемыми. Таким образом, вывод о существовании МГД-резонатора во внешней магнитосфере представляется вполне правдоподобным, что находит свое подтверждение в расчетах, выполненных в более реалистичных моделях среды [Lee, Lysak, 1991; Leonovich, Mazur, 2001].

Во-вторых, обсудим реалистичность рассмотренных механизмов затухания собственных мод. Плазма солнечного ветра и магнитосферы является в высшей степени бесстолкновительной, поэтому пренебрежение столкновительной диссипацией вполне оправдано. Бесстолкновительное затухание Ландау быстрого магнитного звука и альфвеновской волны в холодной плазме также чрезвычайно мало [Ахие-зер и др., 1974]. Остаются два учтенных нами механизма. Поглощение в точке альфвеновского резонанса имеет неустранимый характер. Сколь бы малы ни были эффекты диссипации, это поглощение обеспечивается одним (наибольшим) из них. В окрестности альфвеновского резонанса колебание представляет собой альфвеновскую волну, которая, в отличие от быстрого магнитного звука, даже в продольно неоднородной плазме достигает ионосферы [Dungey, 1954]. Поэтому наиболее важным диссипативным эффектом оказывается омическое поглощение в ионосфере. Затухание собственных мод, обусловленное их убеганием в солнечный ветер, имеет бездиссипативную природу. Его существование не вызывает сомнения, но возникает вопрос: не является ли оно слишком большим? Представляется, что наша одномерная модель вполне разумно описывает явление частичного отражения волны от магнитопаузы и дает правильную оценку параметра δW, характеризующего «проницаемость» магнитопаузы для магнитозвуковых волн.

Третий вопрос, который следует обсудить, – вывод о резонансном характере возбуждения колебаний в магнитосфере. Представляется, что этот вывод является очень общим и имеет место в любой модели среды при условии существования резонатора. Аналогичными свойствами обладают резонаторы самой разной природы – от электротехнических [Каценеленбаум, 1966] до атомных и ядерных объектов [Ландау, Лифшиц, 2004]. Во всех этих случаях зависимость уровня возбуждения резонатора от частоты падающей волны характеризуется наличием максимумов на собственных частотах резонатора. Высота этих максимумов определяется потоком падающей энергии и «проницаемостью» границы резонатора, т. е. тем же параметром δW, что определяет излучательную часть затухания собственных мод. Эти общие свойства целиком находят свое отражение в результатах нашей работы.

Последний вопрос, который мы обсудим, связан с азимутальной асимметрией падения гидромагнит-ной волны на магнитопаузу. Застойная область солнечного ветра примыкает только к лобовой части магнитосферы. На ее флангах скорость течения солнечного ветра велика, и ее наличие нельзя игнорировать. В этих областях важную роль играет неустойчивость Кельвина–Гельмгольца. С ночной стороны солнечный ветер вообще отсутствует. Столь же асимметрично и падение волны на магнитопаузу. Если это падение приблизительно нормально в ее лобовой части, то, конечно, далеко от нормального в других ее частях. Поэтому мы ограничили рассмотрение лобовой частью магнитосферы. Если резонатор в магнитосфере также ограничен по азимуту лобовой ее частью, то наше рассмотрение самосогласованно (с учетом ограничения снизу волнового числа m). Если же резонатор имеет тороидальную форму, охватывая все значения азимутальной координаты, то проникновение в него энергии будет происходить только через своего рода «окно» в лобовой части. Соответственно, ниже будет уровень накачки резонатора, что можно учесть пропорциональным уменьшением параметра δW (но только в отношении проникновения волны извне, для описания убегания волны следует сохранить прежнее значение этого параметра).

Проведенный критический анализ применимости использованной в работе одномерной модели среды дает основания утверждать, что она адекватно отражает основные свойства рассматриваемого явления, дает правильные качественные выводы и правильные оценки важнейших параметров, описывающих это явление.

в ионосферных слоях с учетом того, что E_z=0 и s₂= i (4n / to) д₂, принимает вид

r            r        4irrn r

A E_±-V_±(V_±E_±) = -i — д_±E2 .

c

(П2)

Проинтегрируем его по z в интервале (–Δ, 0). Пренебрегая изменением электрических полей внутри этого интервала, имеем

dE2 | dz z=0

-

r dE2 | dz '

r

¹z=-A     iK 0 E 2 ¹z=0^.

-—

Тензор K₀ имеет вид

K

(П3)

Приложение. Учет конечной проводимости ионосферы

Конечная проводимость ионосферы приводит к изменению граничных условий на ионосферных плоскостях z=0 и z=L. Для вывода этих граничных условий конкретизируем модель среды вне магнитосферного слоя, т. е. при z<0 и z>L. Будем считать, что ионосферные слои имеют малую, но конечную толщину Δ и занимают области (–Δ, 0) и (L, L+Δ). Поперечные компоненты тензора проводимости в этих областях

KP

- KH

K_H

KP

где

4πω

K P,H 2 ^P,H’ c

'

= J ^dP,H

-A

dz ,

л д2

σ

P

σH

E_{P H} - интегральные проводимости ионосферы. Индекс «0» у тензора K^ˆ₀ означает, что он относится к ионосфере z=0. Величины KP и KH имеют размерность волнового вектора. Будем предполагать, что проводимость ионосферы столь велика, что K_PH>> k₂. Тогда, учитывая (П1), приводим (П3) к

-^dH

P

виду

где σP – педерсеновская, σH – холловская проводимости. Как и ранее, будем полагать, что продольная проводимость о_н= ^. Еще далее от магнитосферного слоя, при z<–Δ и z>L+Δ, находятся области, моделирующие нейтральную атмосферу, в которых д ₂= 0, о„ = 0 .

Мы дадим вывод граничных условий в предположении, что проводимость ионосферы достаточно велика, чтобы в главном порядке ее можно было считать идеально проводящей, но ее толщина настолько мала, что возмущенное электрическое поле в пределах ионосферного слоя мало меняется по координате z (однако производная от поля может измениться сильно).

Атмосфера является однородной средой. Для возмущений вида плоских волн дисперсионное уравнение в ней имеет вид к²= kX + k²+ kZ = 0 . Это есть дисперсионное уравнение для электромагнитной волны в вакууме, в котором пренебрегается током смещения, т. е. рассматриваются столь низкочастотные колебания, что можно полагать ω/c→0. Таким образом, к^ = - к², где к²= k_x² + k2 . Возмущение, ограниченное при z→–∞, имеет зависимость от z вида exp(k₂z). В таком случае на границе ионосферы и атмосферы

r дE.          - r дz z=0    iK 0 E2 1 z=0 .

Разрешая это соотношение относительно E₂I_z=0 имеем

r

E2lz =0 = iK 0^-1

Очевидно,

K

^{д E}2I д z

(П4)

Kp² + KH

KP

K_H

K_H

KP

Совершенно аналогично получаем граничное условие для сопряженной ионосферы:

^E2 ^|z=L⁼

r

ˆ

-iK

-1

L

д E2 | дz z=L .

r

(П5)

В пределе идеально проводящей ионосферы, т. е. при KP, H→∞, правые части в (П4) и (П5) исчезают. Поэтому далее мы будем их рассматривать как малые поправки к приближению идеальной ионосферы.

Выясним, как эти поправки изменяют основное уравнение колебаний в магнитосфере (26). Действуя в духе теории возмущений, положим

r

E₂(x, z) = E₂(x) UN (z) + e₂ (x, z),               (П6)

r dE_ r dz z=-A = k2 E2 1 z =-A .

(П1)

Общее уравнение монохроматических колебаний r to2 , r rot rot E = — sE c2

где r₂(x, z) - поправка, обусловленная конечной проводимостью ионосферы. Без умаления общности можно считать, что она как функция z ортогональна решению нулевого приближения:

L

J Un (z) e2 (X, z)dz = 0.                         (П7)

Линеаризация граничных условий по этой поправке дает

—

—

I_z=0,L = ±iUN I_z=0,L • K-LE,(x).

(П8)

Здесь

222 q = q + ikz 8 p .

Параметр εP по порядку величины

(П13)

Отметим, что U'_N Iz=0 = kz и U'_N Iz=L = (-1)Nkz.

Уравнения для E_±можно также получить из (П2), если учесть, что в магнитосфере тензор <5_± имеет только диагональные компоненты, равные -i (to c²/4пcA):

—    to2 —             —

AE_±+ — E_±-V_±(V_±E_±) = 0.

c_A

Подставим в это уравнение разложение (П6), умножим на UN(z) и проинтегрируем по z от 0 до L. С учетом условия ортогональности (П7) получим:

1 c²

8p--=---------

P  K_pL 4nto L E_p

.

Поскольку K_P>> k_±и k_±L ~ k_±l >> 1, то тем более K_pL >> 1 и, следовательно, параметр 8_p<< 1.

В однородной плазме из уравнения (П12) следует дисперсионное уравнение k2

to = to₀-1y, to₀= kc_A, y = —T8_pto₀.

2k²

В области альфвеновского резонанса ω0=kzсА, Y = Ya = ^(1/2)8p ^to0.

L

—— d² E^ dx²

——

⁺(q^{2 -}ky) Ei

—

-V_±(V_±E_±)

+ LUN(z)^de⁽X’z) dz = 0.

о           d z

+

Интегрируя в последнем члене по частям и используя соотношения (П8), приводим уравнение к виду

^— d²E_l dx²

—

+(q2 - ky) E

—

-V_±(V_±E_±) +

+i 2^- (A' + KL^X) E_±= 0.

Введем обозначения

V_±= (-iky, d / dx),

(П9)

где

A e±

,

2K_P              2K_H

^8p= ^ 2 + K2V⁸H = ^ у + k2\t’ ⁽K p + K H ) L         ⁽K p + K H ) L

а знак суммы означает суммирование по сопряженным ионосферам. С помощью этих обозначений уравнение (П9) можно переписать в виде

——

(q²+ ik²z?_±)E_±=-V_±(V_±E_±).                 (П10)

Из соотношений (5), (7), (8) и (25) нетрудно получить, что

—   • 4n® - v±Ei= i— S .

cB₀

(П11)

Это означает, что правая часть уравнения (П10) выражается через функцию g . Но тогда, рассматривая его как алгебраическое уравнение на компонен-— ты вектора E±, можно выразить их через функцию g . Подставляя найденные таким образом значения в соотношение (П11), получим уравнение на эту функцию:

d 2% (./²)' d% 2 ТУ— ^{+ (}q dx q dx

-

k2)S = 0.

(П12)

Работа выполнена при поддержке РФФИ, гранты № 07-05-00185 и № 09-02-00082.