MHD waves in the collisional plasma of the solar corona and terrestrial ionosphere

Plasmas of the solar atmosphere and terrestrial ionosphere are multicomponent media consisting of charged and neutral species. The magnetohydrodynamic (MHD) approach is a valid tool to a good degree for the modeling of large-scale solar and near-Earth plasma phenomena. The success of MHD in the solar photosphere and terrestrial magnetosphere can be seen from comparing the realistic MHD models with observations. In both media MHD waves are ubiquitous [Nakariakov et al., 2016] , and they may act as intermediary transferring energy from vast reservoir of low-energy particles to a small group of high-energy particles.

In solar physics, the study of Alfvén waves, transverse incompressible magnetic oscillations, is very popu- lar due to its appeal to the solar coronal heating, as these waves can be easily excited thanks to the convective gas motions. Only a tiny fraction of this energy, if carried by the Alfvén waves to a higher altitude, will suffice to heat the corona to millions of degrees. Upward propagating Alfvén waves have been validated as a possible mechanism for heating the Sun’s corona by transporting convective energy from the photosphere [Tomaczyk et al., 2007; McIntosh et al., 2011].

The entire near-Earth space environment is filled with MHD waves with time scales from fractions to tens of minutes. These waves are recorded by satellite and ground magnetometers as ultra-low-frequency (ULF) pulsations. The terrestrial magnetosphere is a collisionless medium in the ULF time scale, so ideal MHD approach is an adequate theoretical tool for describing

ULF waves [Menk, Waters, 2013] . However, in the terrestrial ionosphere (altitudes from thousand to few thousand kilometers) particle collisions become significant and the ideal MHD becomes insufficient. Any magnetospheric MHD disturbance can penetrate to the ground only through such collisional medium. Moreover, strong dynamic disturbances in the ionosphere, such as explosive atmospheric impact (seismic shock, hurricane), sudden auroral heating, rocket launches, explosions, etc., can excite transient ULF response [Pokhotelov et al. , 1995] .

The solar atmosphere and terrestrial ionosphere are a mixture of plasma and neutrals with a weakly ionized gas in the bottom layers and a fully ionized plasma in the upper layers. Such partially ionized gas does not behave like fully ionized plasma, and hence the ideal MHD description of these media dynamics at best is a crude approximation [Pandey et al., 2008] . For an adequate interpretation of the magneto–seismology observational results in the solar atmosphere and near-Earth environment it is necessary to consider MHD waves in a partially ionized plasma in a multi-fluid description for the electrons, ions, and neutral gas. Consideration of MHD waves in a collisional plasma indicated not just an occurrence of some collisional damping, but a possibility of new types of MHD waves to emerge [Sorokin, Fedorovich, 1982, de Pontieu, Haerendel, 1998; Balles-ter et al., 2018] .

In our previous studies, we have developed the so called E-approach in a general form, which makes it possible to consider the three-component plasma consisting of electrons, ions, and neutrals with arbitrary ratios between frequencies of collisions between different species [Nekrasov, 2008, 2009] . For astrophysical and space plasmas often consisting of species of many types (electrons, ions, dust grains, neutrals), this multicomponent E-approach considering the dynamics of each species separately has turned out to be an adequate method [Nekrasov, Shadmehri, 2011] .

In this paper, on the basis of the E-approach we derive on the basis of the E-approach a general dispersion relation for the fast magnetosonic and Alfvén waves in a uniform collisional plasma. We consider the case of a low-β plasma where the gradient of the thermal pressure is small as compared with electric, magnetic, and collisional forces. We show that new MHD modes, depending on the ratio between the wave frequency and collisional frequencies, may appear. These relationships can be used to interpret some low-frequency wave processes in the solar corona and terrestrial ionosphere.

1. BASIC LINEARIZED EQUATIONS

A three-fluid version of Ohm’s law describes relations between currents and electric/magnetic fields in a multi-component plasma taking collisions with neutral and ion species into account (e.g., [Song et al., 2001] ). From the momentum balance between plasma components the equations of motion for electrons, ions, and neutrals follow [Zaqarashvili et al., 2011, 2012]

d v „ q „ q _

—e + v e .V v _e = -q -E + - q -v _e x B -d t m _e m _e c

-Vei (ve - vi )-Ven ( ve - vn ) , dv-     _ q _ q „

—i. + vi .Vvi = -q- E + -q- vi x B - dt             mi     mi c

-^V ie ( v i - v e ) -^V in ( v i - v n ) ,                        (1)

dv n n n ne n e ni n i . d t

Here, index j marks electrons (e), ions (i), and neutrals (n), v j is the velocity of species j, q j is their charge, ν_kl is the collision frequency of particle k with particle l, and c is the speed of light. The electric and magnetic fields, E and B , are coupled with particle dynamics by the Faraday’s and Ampere’s equations. The background plasma and magnetic field are assumed to be homogeneous. The background magnetic field B 0 is directed along the axis Z.

From the momentum conservation law, the relation for the different particle collisional frequencies follows ν _i j m _i N _i = ν j _i m j N j , where i, j denote an electron, ion, or neutral. We consider oscillations with small amplitudes, so the collisional terms hold only the background (undisturbed) specie densities. We leave effects of temperatures, pressure, viscosity, and gravity out of account. The background magnetic pressure is supposed to exceed the thermal pressure P , i.e. в = 2 ц Р / B 0 0 1. The ionosphere and inner magnetosphere are examples of such cold plasma. In the solar chromosphere and corona the parameter β < 1 [Rodriguez Gomez et al . , 2019] .

The dynamics of neutrals, described by the third equation from system (1), is determined only by collisions with charged particles. Using equations for electron and ion velocities, we can obtain an equation for plasma density from the continuity condition. Nonetheless, in our consideration the information about perturbed density will not be necessary.

After linearizing Equations (1) and substituting the perturbed velocity of neutrals vn into the linearized equations, we obtain the equation for ion and electron velocities vj, where index j marks electrons (e) or ions (i). For perturbations of the form « exp(ikr - itot), the equations of motion become algebraic and the determinant of this system gives the dispersion relation in a general form qj

- i to₽ j v j = F j +—- v j x B ,                      (2)

mjc where

F e = qe" E -^a e ( v e - v i ) , m _e

F i = q^- E -a ( v i ^- v e ) .

m _i

Here, we introduce notations

. V ee = 1+-en-, ei = 1+-i^, an         an

I .   V V  )             I .   V V)

ae =Vei|1 + -en-ni- I, ai =Vie 11 + -ne-i^L

I    anVei J           I    anVie an =-ito + (Vne +Vni ).

This equation enables us to consider different relations between the wave frequency ω and collisional frequen-

МГД-волны в столкновительной плазме солнечной короны cies ν_ne+ν_ni. The solution of Equation (2) may be presented as

° U j . to F - i ®P j F j x ,

° U j y =-® j F jx — i ®₽ j F jy ,                        (4)

^- i top j u j z = F z ,

where ° 2 = to 2 -p ² to ², and to j = qB⁰ is the cyclotron m j c

frequency (index j marks electrons and ions).

2. PERTURBED CURRENT AND DIELECTRIC TENSOR

We now find the perturbed current J = ^ q j N j v j = q i N ₀ ( v i - v _e ) . The condition of quasineutrality N _e= N _i= N , and q _e=- q _i, has been assumed. Using equation (2) for the transverse velocity and taking into account equations (4), we obtain the following relationships

aJ x + bJ = qN- ( dE y - i ^to E x ) , a ^Jy ^{- bJ}x = q i- N i" ( ^{- dE}x ^- i ^to fE y ) .

m _i

3. DISPERSION EQUATION

From Faraday’s and Ampere’s laws we can obtain the equations for perturbations. Using equations (7) and (8), we find

(n2 -exx)Ex - exyEy = 0, e xyEx +( nz - Exx ) Ey - nynzEz = 0,                 (9)

-nynzEy +(n2- ezz ) Ez = 0, where ny z =( ky, kz) c I to is the refraction index of plasma, and n2 = n2 + n2.

Components ε _xx , ε _xy , and ε _zz given by equations (7) and (8) in a general form can be applied to arbitrary ratios between collision frequencies and wave time scales. This enables the study of wave propagation in a partially ionized plasma in different domains of the solar atmosphere or terrestrial ionosphere. Below, we consider specific important cases. We first consider waves propagating almost along the background magnetic field when k_y →0 (quasi-parallel propagation), and then the oblique wave propagation, k y ≠0.

Here, the notations are introduced

. [ Рд P a |       tojttj a = 1 - i to -V + -eV- , b = —V + l °2   °2 )°

, to; toe m; , P; Pe m; d = -V +     , f =+

^to e ^a e

° 2 ,

3.1. Longitudinal propagation

The condition for the quasi-parallel (field-aligned) propagation k_y →0 can be found from the inequality n 2 0 e xy . As follows from Equation (9), the dispersion relation D (ω, k_z )=0, where D(ω, k_z ) is the determinant of the system (9), for the field-aligned propagation of MHD modes is

.

z xx x xy y .

The solution of Equation (5) for the perturbed J x,y is as follows

( ^{4 n} i I ^to ) J = 6 xx E x + S xy E y ,

(4ni I to) J = -e Ex + eE , y       xy x xx y where

currents

6 xx

^£ xy

to pi

( a ² + b ²) to Pi

ibd    „)

----⁺ af I , to        )

iad

( a ² + b ² ) l to

- bf

and to pi = ( 4 n q ² N i / m i )    is the ion

plasma frequency.

From equations (2) and (4), we find the perturbed

longitudinal (field-aligned) current J_z = q i N ₀ ( as follows

4 n i т c

Jz = 6zzEz , to

- u )

e z

^e zz

^to pi

- i to

1 a; aE | - i to+ —L + — l       l P i P e J J

| 1 m i 1 ] 1+I lP , m e P e )

.

The contributions of ions and electrons into the wave dynamics can be easily estimated separately from Equations (7) and (8).

This equation describes two circularly-polarized waves: the fast magnetosonic and Alfvén modes. Their electric fields rotate in opposite directions in the plane perpendicular to the magnetic field B 0 .

To find the tensor elements and resulting dispersion equation, we must specify collision frequencies and timescales. From the dispersion equation for MHD modes we consider separately three limiting cases and derive relationships for a phase velocity V and damping rate.

3.1.1. Weakly collisional plasma

First, we consider a weakly collisional plasma when to i ^ to ^ v _in. In this case, neglecting factors ж v _in I to 0 1, the terms in (3) and (6) are simplified as follows a_n.- i го, a_e.v_ei+ i v_env_niIm, a i .v_ie+ i v_nev_inIto, e i . 1, e e — 1, a . 1, b . a i I to i +a_eI to e , d . 0, and f . to - ². The elements of the tensor reduce to the following

^to pi      C 2               , ^to pi

. — = 70, ^e xy . ^{- b}— .

to ²     V 2              to ²

Relationships (11) show that the off-diagonal elements in (9) are small as compared with ε xx , ε xy <<ε xx , and can be neglected. Therefore, the resulting dispersion equation may be reduced to

( n_z 2 -e xx ) = 0.

From (12) it follows that the wave phase velocity along the magnetic field is the ordinary Alfvén velocity ω/ k z = V A = B /[4πρ i ]^{1 / 2}.

The influence of weak collisional effects can be estimated keeping the collisional terms « v _in / to in the dispersion relationship (12)

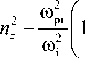
v v ne in to2

—

V CO I i— 1 = 0. to )

The resultant relationship for the wave phase velocity takes the form

to = y

1     V A kz

f 1 ^- ne ^- .n I + i V^ l 2 to 2 )    2 to 2

Thus, in the case to ^ v _in the MHD eigenmodes are weakly damping Alfvén and fast magnetosonic waves. Their phase velocities, given by (13), are somewhat lower than the Alfvén velocity V A .

3.1.2. Collisional plasma with moderate ion-neutral coupling

Now we consider somewhat lower frequencies, when vni 0 to 0 vin, where vni is the neutral-ion collision frequency. In this case, neglecting small terms « to / vin 0 1, the relations (3) and (6) are simplified as follows: an.-im, ae.vei+ivenvni/m, ai.vie+ivnevm/ff>, PciVen/m,         Pi.ivin/m,          a . 1- vin ai / Q2, b . bVa / to3, d . b2to2 / to3, and f . P; /Q2. The i ii    ii       i i tensor elements reduce to the following

s

xx

P i to pi

^Q 2 ^—v _m ^a i

^s xy

topi to2)

0 s _xx

^s yy = ^s yx . °.

As a result, dispersion relation (12) takes the following form

2                 toPivin nz + ■ / 2           \         2     °.

i ^to ( ^to i ^{— v} ie^v_m ) ^{+ v} _n e^v_m

In the case of a weak B -field, when v ² _n v _ne ^ toto ², we arrive at the following dispersion equation and the relation for the phase velocity

₂                                           1/2

, to„:            (Г)            | V V I nz2 + —pi- = °, — . iVAI-“l .         (14)

^v in ^v ne       kz        l to )

In the case of a strong B -field, when toto _i ² » ton^v ne , we obtain

2 topi vin n to n2 + p T — °,   . — ikz A.(15)

i totoi         kz

Thus, in the case vni 0 to 0 vin   all MHD eigenmodes are to be severely damped.

However, at very low frequencies, when neutrals and ions become strongly coupled, a possibility of weakly damping MHD modes, named decelerated MHD modes, emerges. This case is considered below.

3.1.3. Dynamics of strongly coupled neutrals and ions

Now we consider the low-frequency limit in which to 0 v _ni. In this case, neutrals are strongly collisionally coupled with ions. Neglecting small terms ∼ ω/ν_ni, we obtain from (6) that a n . v_ni, a_e. v_ei+ v_en, a i . V ie + V ne V_m/V ni , P i . 1+ P n /P i , e e . 1+ V en /V ni ,

a . 1 — i to ^ P i a i / Q i ² +P _e a _e / Q 2 ) , b . p ² to ² a i / to ³, and d . to ² / Q ² + ( to 22 / Q 2 ) ( m i / m _e ) . As a result, dispersion relation (12) reduces to the following form

n_z ²

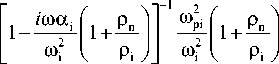
From the relationship (16) the relation for phase speed of Alfvén wave can be obtained with account for collisions

to = y

- V A

kz

^"

i ^toa i [     p n

1 I 1 +

^{2 to} i l     P i.

Here V A is the modified (decelerated) Alfven velocity

^V A = ^B 0 / [ ^{4 n} ( P i +P n ) ] ‘^/2 .

Unlike the ordinary Alfvén velocity V A , the modified velocity V _A is determined by total density of ions and neutrals, ρ i +ρ n .

To elucidate the physics of decelerated MHD modes we may consider the neutral velocity V n in a wave

К v n            ni

— .

^V i    ^v ni ^— i ^to

According to this relationship, in the frequency interval v _in 0 to , corresponding to a weakly damping MHD mode in Section 3.1.1., the velocity of neutrals is much lower than the ion oscillatory velocity, V _n 0 V i . Therefore, neutrals are not involved in the wave propagation, and wave propagates with the Alfvén velocity with a weak attenuation. On contrary, in the low-frequency limit, to 0 v _ni, corresponding to a decelerated MHD mode in Section 3.1.3, neutrals are involved in a joint oscillatory motion with ions, V _n . V i . In other words, MHD waves are mass-loaded with neutrals [Vranjes et al., 2008] .

• 3.2.    Oblique Propagation

• 3.2.1.    Alfvén mode

We now consider the case of oblique wave propagation when k_y ^ ° . Assuming that n y ^ s xy , the terms ^ s xy E x _y describing the Hall effect can be omitted. Then, we obtain the following dispersion equations

(n ² —s„ EE — — °, ( n _z² —s„ EE — — °.              (18)

xx x            z xx y

Equations (18) describe the independent linearly polarized magnetosonic, E x * °, and Alfven, E_y * °, waves.

For Alfvén waves, we include the contribution of the field-aligned field E z and find the dispersion relation

МГД-волны в столкновительной плазме солнечной короны nZ -E x + n2 — = 0, e zz

where εzz given by equation (8) has the form e zz

—

® 2e to ( toP e + i a e )

where ω_pe is the electron plasma frequency. The ions do not contribute to the longitudinal current due to their high mass in comparison with the electron mass. In ideal MHD it is assumed that ε zz →∞, and E z is neglected.

We consider only the most interesting case to 0 v ni . In this low-frequency limit, we have

«e.Vei+ Ven,     ee. 1+Ven/Vni,     toPe 0 ae, and to(1 +Ven/ Vni ) 0 Vei +Ven. Using (19) and the condition of quasi-neutrality αi=(me/mi)αe, we find from (19) the dispersion relationship to2 + i ne k 2to — kz VA = 0.

The factor n _e = a _e c ² / to pe describes the magnetic diffusivity of Alfvén waves. From this relationship the relation for the phase speed of oblique decelerated Alfvén wave can be obtained

Г = V aJ¹ — i n e k_z

k ² to

k z V 2

• 3. 2.2. Compressional mode

We consider fast magnetosonic (compressional) waves, described by the first equation (18), in the low-frequency limit with a strong collisional coupling of neutrals with ions, to 0 v ni . Neglecting small terms «to / v _ni 01, we obtain from (6) that a _n .V_ni, a e . V ei + V en , « . V ie + V_n e V_m/V ni , e i ^ 1+P n /P i , e e . 1+V en /V ni , a . 1 — i to ( P ; a i / Q 2 +P e a e / Q 2 ) , b . p ² to ² a i / to ³, and d . to i / Q ² + to _e/ Q 2 ( m i / m _e ) . As a result, the dispersion relation (18) reduces to the followingform

I to2 + inik2to — k2VA = 0, ni = -vl vie +-ne-in topi I         vni

.

The phase velocity with account for the collisional correction ∝ iηi is as follows to |,    .Hik ]

— . V 1 — i .

k A I       2 V ^A I

Thus, the low-frequency fast compressional mode propagates in a collisional plasma with a reduced Alfvén velocity V _A and a weak damping.

• 4.    DISCUSSION

  The above consideration has shown that in a weakly ionized plasma a new type of MHD waves are possible, named decelerated MHD waves [Ballester et al., 2018] . These decelerated MHD waves should not be mixed up with the ordinary slow ion-acoustic mode. In decelerated MHD waves the neutral component is involved in oscil-

• MHD waves in the collisional plasma of the solar corona lation together with ions. These weakly damping waves may exist under condition T ^ т . v—1, where T is the wave period.

The occurrence of new modes in a strongly collisional ionospheric plasma was demonstrated by Sorokin and Fedorovich [1982] . They analyzed the relationship for the current j generated by oscillations of plasma with velocity V which may be described by the simplified Ohm’s law

. to           to_eto                 e ² N

• v,    j — “ j ^x B + — ^e ir B ^x j ^x B =---- E ,

• 4.1.    Solar atmosphere

e B        vin B2             m , where E′=E+c-1V×B. The wave phase velocity and damping rate of MHD waves are determined by the parameter Vni. At frequencies to 0 vni ions can drag neutrals into the wave dynamics, so a collisional plasma oscillates as an entity. In this case, the propagation velocity VA is determined by the total medium density, comprising both ions and neutrals. If the ionization rate is low, Ni / Nn 0 1, the velocity of decelerated MHD mode is much lower than the classical Alfvén velocity. Our more general consideration has confirmed the existence of decelerated MHD modes and has enabled us to estimate the damping rates of those modes.

To highlight the physical nature of the MHD modes modified by a strong collisional coupling we have considered the wave properties in a homogeneous system. In realistic situations, a steep inhomogeneity of plasma or magnetic field may result in the formation of Alfv´enic resonators and compressional mode waveguides. Though formally mathematically the Alfvén mode has no turning point, a substantial wave reflection may occur in regions with a strong contrast between the transverse Pedersen conductance Σ P and wave conductance Σ_A=(μ_o V _A)^-1 [Yumoto et al., 1995] , field-aligned gradient of Alfvén velocity [Cally, 2012] , or rapid variation of the curvature of magnetic field lines [Pilipenko et al., 2005] . As a result, Alfvénic resonators can be formed between these regions. The waveguides where the fast magnetosonic (compressional) modes can be trapped are formed in the regions with a deep minimum of Alfvén velocity. To justify a possibility of the guided decelerated MHD wave propagation a profile of the modified Alfvén velocity V _A ( z ) should be constructed from available empirical models.

We suppose that the background magnetic pressure exceeds the thermal pressure P , that is P = 2 p P / B 0 0 1. The approximation of cold plasma is valid in the terrestrial ionosphere and inner magnetosphere, and in the solar chromosphere and corona. Moreover, even a finite value of β does not influence qualitatively the properties of large-scale MHD waves: a thermal pressure does not modify the Alfvén mode, whereas the fast magnetosonic mode a thermal pressure acts additively with magnetic pressure.

We neglect the influence of a gravity. A possible modification of low-frequency MHD waves may occur upon account of gravity resulting in a stratification of plasma density [McLellan, Winterberg, 1968]. The contribution of gravity effects into the ideal MHD theory is characterized by the effective height H. U2/g, where U2 = {VS2, VA}. The gravity-modified MHD modes were called magneto-gravity waves (MGW) alike acoustic-gravitational waves. The gravity effects can be neglected when kH ^ 1. In the ionosphere, the estimated scale H is much larger than any possible wavelength of ionospheric modes ∝ k-1, so the effect of gravity can be neglected. Moreover, the consideration of gravity effects in [McLellan, Winterberg, 1968] was performed in the ideal MHD theory regardless of collisional effects.

The solar atmosphere is a partially ionized medium with fractional ionization changing with altitude. The lower solar atmosphere — the photosphere, is a weakly ionized medium, and though with increasing altitude the fractional ionization drops, even in the chromosphere the neutral number density dominates over the plasma density by an order of magnitude. In the upper transition region and corona the solar plasma is fully ionized, but in the photosphere and chromosphere up to low transition region it is only partially ionized.

In the photosphere, the ionization rate N i / N n varies with altitude from ∼ 10^-4 to ∼ 1. The collision frequency ν in varies from ∼ 10⁹ to ∼ 10² Hz [Pandey et al., 2008] . Therefore, the neutral-ion collision frequency ν ni may vary from ∼ 10⁵ to ∼ 10² Hz. Thus, Alfvén and fast magnetosonic waves with frequencies much lower than the effective neutral-ion collision frequency v_n i . 10 2 Hz have to propagate in the photosphere with a low damping due to a strong collisional coupling of ions with neutrals partaking in oscillations together.

The solar prominences is only a partially ionized medium as well. The condition of the strong collisioncoupling between neutrals and ions is valid for wave periods T >30 s. Thus, the prominence oscillations [Balthasar et al., 1993; Foullon et al., 2009] observed with such periodicity may be interpreted as decelerated Alfvén waves with strong neutron-proton collisional coupling.

The emergence of new modes, named modified fast and slow waves, owing to a strong coupling between charged and neutral particles in solar plasma was shown by Ballester et al. [2018] . In general, our results agree with that from [Ballester et al., 2018] , but in their study the electron-neutral collisions have not been taken into account. Additionally, we provide the relationships for the phase velocities and damping rates that are useful for the comparison with observations.

• 4.2.    Terrestrial ionosphere

  In the terrestrial ionosphere, gyrofrequencies of electrons, ro e . 10 6 s^-1, and ions, m i . 10 2 s^-1, do not vary much with altitude. In the dayside ionosphere the ion density is N , .3^10 5 cm^-3 in the E layer (120 km) and N .3-10⁶ cm^-3 in the F layer (350 km). Corresponding values of the neutral component density are N n .10¹¹ cm^-3 and N n . 10 9 cm^-3 in the E and F layers resp ectively. Therefore, the ionization rate is N i / N n ~ 3·10^-6 in the E layer, and N _i/ N _n ~ 3·10^-3 in the F layer.

• 5.    CONCLUSION

  Using the multi-component approach, earlier developed in [Nekrasov, 2008, 2009] , we have considered a model of collisional three-component cold plasma consisting of electrons, ions, and neutrals. This approach makes it possible to follow the movement and change of parameters of each species separately and to obtain the corresponding physical consequences. The dielectric tensor elements in a partially ionized plasma have been derived in a general form, so they can be applied to arbitrary relationships between collision frequencies of species and wave timescales. For a collisional plasma we have derived the dispersion equation and relationship for the phase velocity for MHD modes for three limiting cases: a weakly collisional plasma, a moderate collisional plasma, and a strongly collisional plasma. The critical parameter that determines the wave regime is the ratio between the wave period T and the time of

Collision frequencies can be estimated using classic relationships with the help of the standard model of neutral ionosphere CIRA. According to this model, electron-neutral collision frequency ν en varies from ∼ 10¹⁰ Hz in the D layer (60–70 km) to ∼ 10³ Hz at altitudes above 150 km. The ion-neutral collisional frequency varies from ν in ∼ 10² Hz in the E layer to ν in ∼ 1 Hz in the F layer. Thus, the neutral-ion collision frequency ν ni varies from ∼ 10^-4 Hz in the E layer to ∼ 10^-3 Hz in the F layer. Therefore, the critical time scales that determine the possibility of the decelerated MHD wave occurrence is T * . 160 min in the E layer and T * . 16 min in the F layer. In a partly ionized plasma, electromagnetic disturbances with periodicity larger than the critical time scale T * may be associated with decelerated MHD modes.

In early experiments with powerful impact onto the ionosphere by rocket launches a specific type of ionospheric disturbance in the F layer was noticed [Karlov et al., 1980] . At a distance around 2000 km from a launching site, a sudden decrease in the ionospheric density was detected after ∼ 50 % of rocket launches [Tribble et al., 1989] . The apparent propagation velocity of these ionospheric disturbances was above 30 km/s, so they cannot be associated with internal gravity waves in the upper atmosphere. Some evidence for the occurrence of very low frequency periodic disturbances in the terrestrial ionosphere has been found by Barkhatov et al., [2014] . Quasi-periodic geomagnetic disturbances in the frequency band 10^-5 - 10^-3 Hz were associated with waves generated by the auroral electrojet during substorms [Barkhatova et al., 2009] . Such very long-period ( T> 20 min) disturbances in the ionosphere may be interpreted as decelerated MHD compressional mode (considered in the Section 3.2.1).

According to the above theoretical estimates, low-frequency MHD waves propagate not with Alfvén velocity (which is about several hundred km/s in the F layer), but with velocity about few tens of kilometer per second. This velocity is higher than the typical velocity of the acoustic-gravity waves (few hundreds of meter per second), and corresponds to the disturbance velocities observed after a strong impact on the ionosphere.

МГД-волны в столкновительной плазме солнечной короны the neutral dragging by ions - ν _n ^- _i¹. The consideration based on the multi-fluid hydrodynamics confirms the existence of specific decelerated MHD waves with phase velocity much less that the classical Alfvén velocity. These theoretical results can be applied to different parts of the solar photosphere and terrestrial ionosphere. For the partially ionized plasma of the solar photosphere with a strong collisional coupling of neutrals with ions, the occurrence of weakly damping low-frequency Alfvén waves modified by neutrals becomes possible. In the terrestrial ionosphere, decelerated fast compressional MHD modes can propagate along the F layer of the ionosphere with velocities higher than the typical acoustic velocity.

This research was supported by the state contracts with IPE (AKN) and SRI (VAP). The useful comments of both reviewers are appreciated.