Минимизация избыточной величины крутящего момента в шарнирных узлах многоразового раскрытия-складывания

Появление перспективных проектов космических буксиров, заправщиков и других средств обслуживания космических аппаратов ставит новые требования перед космическим аппаратом во время срока его активного существования. При перемещении космического аппарата такого типа между его рабочими орбитами появляется необходимость многоразового складывания механических устройств солнечных батарей в транспортировочное положение с возможностью их последующего раскрытия в рабочее положение [1–4].

Конструкция механического устройства солнечной батареи многоразового раскрытия и складывания состоит из раскрываемых панелей солнечной батареи и штанги, соединенных между собой посредством шарнирных узлов (ШУ) многоразового раскрытия-складывания [5; 6].

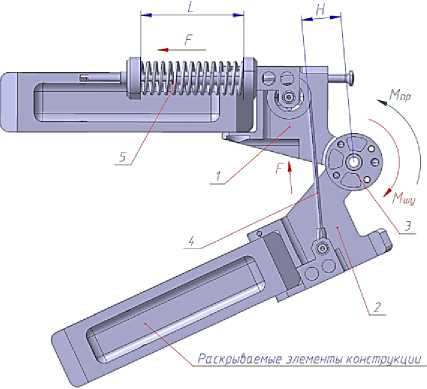
Шарнирный узел многоразового раскрытия и складывания, показанный на рис. 1, состоит из упорного кронштейна шарнира (1), приводного кронштейна шарнира (2), ролика, механически жестко связанного с приводным шарниром (3), троса (4), пружинного привода (5).

Процесс раскрытия-складывания ШУ показан на рис. 1 и включает в себя два этапа [7]. Первый этап раскрытия или складывания ШУ происходит под действием крутящего момента М _пр , который

КИЕ АППАРАТЫ И

передается на ролик от электромеханического привода и вращает приводной кронштейн относительно упорного вокруг их общей оси вращения в сторону раскрытия или складывания ШУ. При этом на приводной кронштейн от упорного через трос действует усилие F сжимающейся пружины, которое возникает вследствие уменьшения величины L пружинного привода. Усилие F , действующее на расстоянии H от оси вращения шарнира, создает крутящий момент М _шу , направленный противоположно М _пр и препятствующий вращению приводного кронштейна шарнира. Таким образом происходит преодоление момента сопротивления М _шу движущим моментом М _пр до того положения, при котором трос пересекается с осью ШУ и плечо H не становится нулевым.

Том 5

Основным требованием, предъявляемым к шарнирным узлам, является величина крутящего момента М _шу в конце раскрытия или складывания, которая должна быть максимальной и достаточной для преодоления всех сил сопротивления и полного перевода и фиксации элементов конструкции в конечные положения.

• 1.    Анализ величины крутящего момента шарнирных узлов многоразового раскрытия-складывания

Величина крутящего момента М _шу зависит от угла поворота ШУ α и выражается формулой (1):

M шу ( а ) = F ( а ) • H ( а ).            (1)

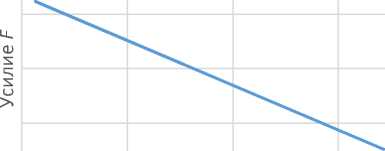
Зависимость величины усилия F от величины сжатия L, характерная для спиральных пружин сжатия, имеет общий вид, показанный на рис. 2.

Сжатие L

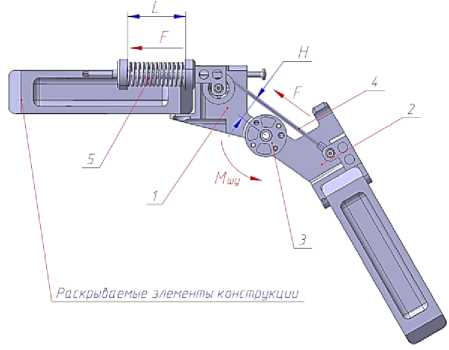
Рис. 1. Шарнирный узел многоразового раскрытия-складывания

Второй этап раскрытия или складывания ШУ происходит под действием крутящего момента М _шу , который меняет свое направление на противоположное и способствует раскрытию или складыванию приводного кронштейна ШУ до перевода его в крайнее положение.

0  20  40  60  80 100 120 140 160 180

Угол поворота а°

Рис. 2. Формы зависимостей усилия и сжатия пружины

Значение сжатия L зависит от угла поворота и геометрических характеристик ШУ. В общем виде форма зависимости сжатия пружины L от угла поворота шарнирного узла α показана на рис. 2.

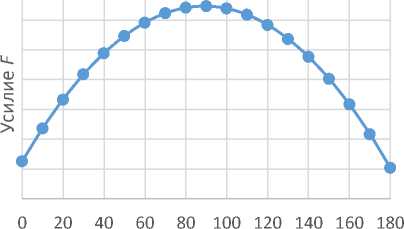
Таким образом, функция зависимости усилия спиральной пружины сжатия от угла поворота шарнирного узла многоразового раскрытия-складывания F (α) будет иметь вид, показанный на рис. 3.

Угол поворота α°

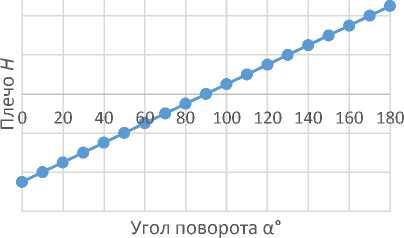
Рис. 3. Зависимости величины усилия пружины и величины плеча от угла поворота шарнира

Форма зависимости плеча H от угла поворота ШУ определяется геометрической компоновкой ШУ и имеет линейный характер (рис. 3).

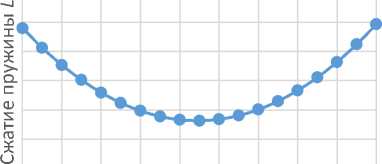
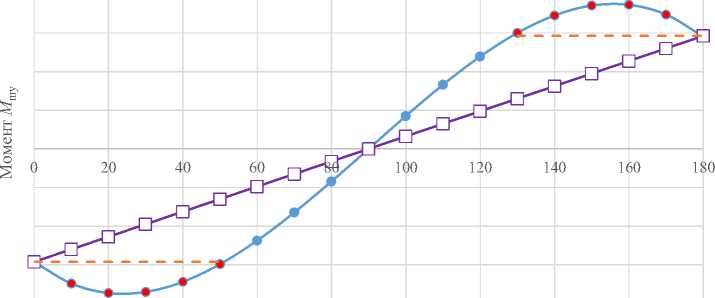
Используя формулу (1), была получена форма зависимости крутящего момента М _шу от угла поворота для ШУ многоразового раскрытия-складывания с использованием спиральной пружины сжатия (рис. 4).

Исходя из полученных теоретических данных видно, что форма зависимости М _шу от угла поворота ШУ, показанная на рис. 4, имеет нелинейный характер. При этом максимальная величина крутящего момента регистрируется при повороте ШУ на угол 25° и 155°, превышает необходимую в конце раскрытия или складывания и является избыточной.

Так как в течение первого этапа движения ШУ раскрытие или складывание происходит путем преодоления момента сопротивления М _шу крутящим моментом М _пр , передающимся от электромеханического привода, появляется необходимость применения более мощного электромеханического привода и увеличения прочностных характеристик ШУ вследствие действия больших изгибающих моментов в процессе раскрытия, что приводит к увеличению массогабаритных характеристик шарнирного узла.

Причиной возникновения зон избыточного крутящего момента является непостоянство зависимости величины усилия от сжатия и нелинейность зависимости величины сжатия пружины от угла поворота ШУ (рис. 2). Так как нелинейность зависимости величины сжатия пружины от угла поворота ШУ обусловлена особенностью конструкции шарнирного узла и принципом его работы, исключение возникновения зон увеличения крутящего момента без изменения конструкции ШУ возможно путем изменения характера зависимости величины усилия пружины от ее сжатия.

Использование пружины, генерирующей постоянную величину усилия на всем промежутке движения троса, позволяет получать линейную зависимость величины крутящего момента от угла поворота шарнирного узла (рис. 4).

—•— Спиральная пружина сжатия

Пружина постоянного усилия

Угол поворота шарнира α°

Рис. 4. Зависимость величины крутящего момента от угла поворота шарнира

(оСМИЧЕскиЕ

АППАРАТЫ И

Том 5

2.    Расчет пружины постоянного усилия

Пружины постоянного усилия применяются в составе приводов механических устройств космических аппаратов, при этом во время своего хода они способны оказывать постоянное усилие, неизменное по величине в пределах рабочей деформации пружины [11; 12]. Пружины изготавливаются из листового материала специально подобранной формы и обладают начальным усилием плотно намотанного рулона.

• ³⁸ В настоящее время наиболее распространенным материалом, из которого изготавливаются

  пружины данного типа, является нержавеющая сталь «AISI 302» ГОСТ Р 58127-2018 (EN 102703-1.4310).

Несмотря на широкое использование пружин постоянного усилия, существующие процедуры анализа и расчета пружин постоянного усилия являются неполными и неэффективными [13–15].

Для осуществления расчета усилия пружины F необходимо определить материал пружины и ее основные геометрические характеристики [16].

Механические характеристики материала, необходимые для расчета:

• •    коэффициент Пуассона µ;

• •    временное сопротивление на разрыв (предел прочности) σ _в (Па);

• •    модуль упругости E (Па);

• •    относительное сужение ψ.

Геометрические параметры пружины (рис. 5):

• •    внутренний радиус R (мм);

• •    толщина пружины t (мм);

• •    ширина пружины b (мм).

С целью увеличения эффективности процедуры расчета усилия требуемой пружины необходимо учитывать количество циклов работы устройства, так как исходя из зависимостей, описанных в ГОСТ 25.504-82, видно, что в условиях малоцикловой нагрузки расчетный предел прочности может быть задан больше, чем теоретический. Увеличение значения предела прочности влияет на максимально возможное значение толщины пружины, от которой зависит генерируемое ей усилие [16].

Таким образом, после определения геометрических характеристик и выбора материала пружины необходимо определить количество циклов работы пружины N . Расчет уточненного значения предела прочности σ ^* согласно ГОСТ 25.504-82 производится следующим образом:

• о * = e / 3,5 -° в _ n __Од2 ₊      — n __Од2 ^. (2)

в

V E            1 “V       )

Для дальнейшего расчета необходимо определить максимально возможную толщину пружины t _max , при которой она сможет нормально функционировать при выбранных геометрических характеристиках и условиях эксплуатации:

t max =2⋅σ ^*в ⋅ R ⋅ ^{1 -µ 2} .               (3)

E

После определения максимального значения толщины пружины t _max необходимо выбрать наиболее близкое значение толщины t из имеющихся вариантов конфигураций пружин и произвести расчет усилия F , генерируемого пружиной:

F = E • b •   t—^ - ( 1 -ц² )

24 - R ^{2 v      7}

Используя приведенный выше алгоритм расчета пружин постоянного усилия, возможно вычислять необходимые геометрические параметры пружины при заданном требуемом усилии, решая задачу в обратном порядке.

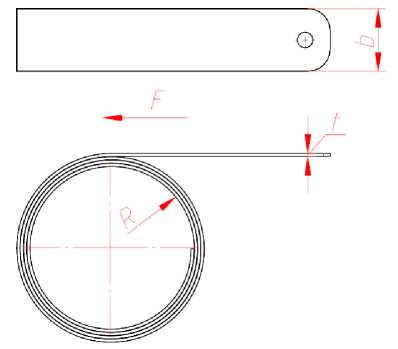
Рис. 5. Условное представление пружины постоянного усилия

Для автоматизации процесса расчета пружин данного типа была разработана программа, в которую заложены алгоритмы расчета, представленные формулами (1)–(4). Интерфейс программы представлен на рис. 6.

Параметры материала пружины

Коэффициент Пуассона:

Геометрические параметры пружины

Толщина пружины

Число циклов:

Предел прочности:

Модуль упругости:

Относительное сужение:

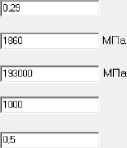
Ширина пружины:

Внутренний радиус:

Максимальная

Параметры расчета

Задаваемая

Произвести расчет

Усилие 114,73

Внутренний рлйиус

Расчет максимальной толщины пружины

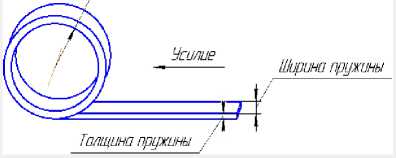
Рис. 6. Интерфейс программы

Выход |

3. Экспериментальные результаты измерений

С целью верификации предложенного алгоритма расчета пружин постоянного усилия был проведен сравнительный анализ на соответствие расчетных данных с действительно измеренными значениями усилия пружин, конфигурации которых представлены в табл. 1.

Таблица 1

Характеристики экспериментальных образцов

№ образца (пружины)	Характеристика	Значение
Пружина № 1	Диаметр	16 мм
	Ширина	16 мм
	Толщина	0,2 мм
	Расчетное усилие	14,7 Н
Пружина № 2	Диаметр	30 мм
	Ширина	20 мм
	Толщина	0,32 мм
	Расчетное усилие	28,56 Н
Материал пружин: нержавеющая сталь «AISI 302»

Измерение усилия пружин проводилось разрывной машиной «EUROTEST T-50» с использованием специально разработанной оснастки. Условия проведения эксперимента представлены на рис. 7.

Экспериментальные результаты измерений усилия пружины № 1 и пружины № 2 представлены в виде графиков, показанных на рис. 8.

Исходя из полученных экспериментальных зависимостей усилия пружины от перемещения, расчетная величина усилия соответствует измеренной при растяжении (раскручивании) пружины. Величина усилия при сжатии (скручивании) пружины оказывается меньше расчетной по причине возникновения сил трения между слоями пружины и трением между барабаном и осью [11; 12].

Для подтверждения работоспособности шарнирного узла многоразового раскрытия-складывания с использованием пружины постоянного усилия был смоделирован и изготовлен прототип шарнирного узла, представленный на рис. 9.

Для проведения испытаний шарнира были использованы ранее рассчитанные и испытанные пружины постоянного усилия, характеристики которых представлены в табл. 1. Графики зависимости расчетных и экспериментальных значений крутящего момента шарнирного узла от угла его

Рис. 7. Процесс измерения усилия пружины

Том 5

Растяжение пружины №1      Сжатие пружины №1          Расчетные значения

Растяжение пружины №2      Сжатие пружины №2

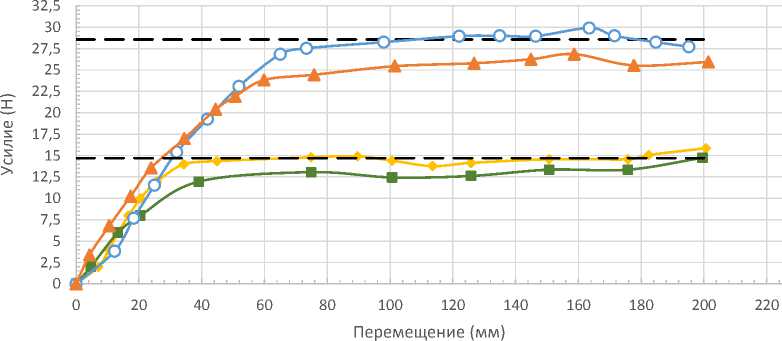
Рис. 8. Результаты измерений усилия пружин

Рис. 9. Прототип шарнирного узла

Раскрытие ШУ с пружиной постоянного усилия

Раскрытие ШУ с эквивалентной спиральной пружиной

Складывание ШУ с пружиной постоянного услилия

Складывание ШУ с эквивалентной спиральной пружиной

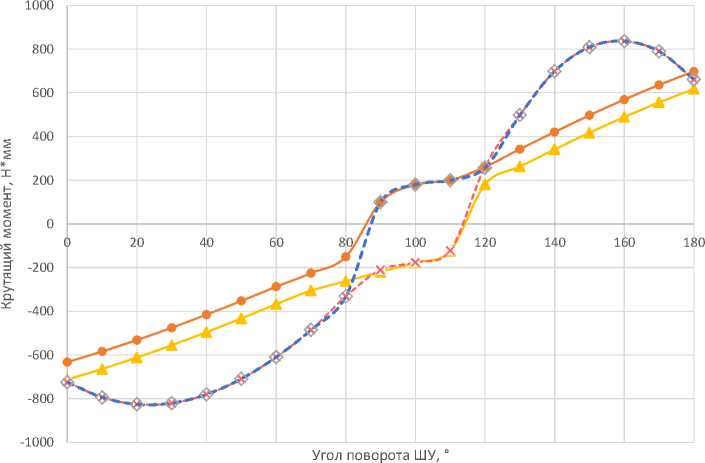
Рис. 10. Результаты испытаний ШУ многоразового раскрытия-складывания

поворота для пружины № 2 и для эквивалентной спиральной пружины представлены на рис. 10.

Изменение формы зависимости на участке поворота 80–110° обусловлено тем, что в подвижных элементах оси ШУ возникает максимальная сила реакции опоры, что приводит к увеличению силы трения, а вследствие и момента сопротивления раскрытию ШУ.

Заключение

Для рассмотренного шарнирного узла требуемой величиной крутящего момента в конце процесса раскрытия или складывания является величина не менее 600 Н∙мм. Шарнирный узел с обоими типами пружин удовлетворяет поставленному требованию. В случае применения пружинного привода со спиральной пружиной сжатия максимальное значение крутящего момента составляет 815 Н∙мм. При применении пружины постоянного усилия максимальное значение величины крутящего момента генерируется в конце процесса раскрытия или складывания и соответствует требуемому, что позволяет использовать электромеханический привод на 26 % менее мощный, чем в случае применения пружинного привода со спиральной пружиной, с условием выполнения поставленных перед шарнирным узлом технических требований.

Таким образом, минимизация величины крутящего момента шарнирных узлов многоразового раскрытия-складывания позволяет снизить общую массу конструкции механического устройства солнечной батареи путем использования электромеханического привода минимально необходимой мощности. Также, вследствие уменьшения изгибающих моментов, действующих в процессе раскрытия, возможно уменьшение количества материала силовых элементов конструкции шарнирного узла, что дополнительно снизит массу конструкции.