Минимизация погрешностей определения координат геофизических скважин

Координаты пространственного положения забоя обсаженных и необсаженных скважин определяют на основе регистрации времени распространения акустических сигналов. Одним из направлений совершенствования методов сейсморазведки является совершенствование способов и средств возбуждения упругих колебаний [2,3]. Обычно генерируемый сигнал распространяется в виде продольной волны, однако вследствие отклонения геометрических и весовых характеристик генератора сейсмических колебаний (ГСК) возможно возбуждение поперечных волн, приводящих к смещению вектора колебательного ускорения в точке приема. Целью данной работы является рассмотрение одного из вариантов уменьшения величины поперечной волны.

Схема генератора сейсмических колебаний минометно-плунжерного типа приводится на рис.1.

Рис.1. Схема установки ГСК: 1 - миномет, 2 – плунжер, 3 – контейнер, 4 – направляющая

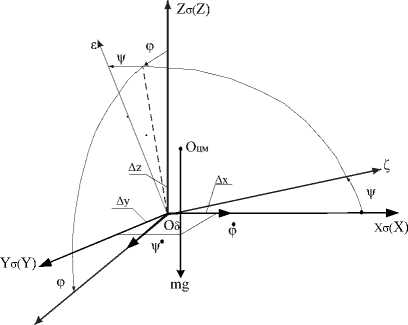
Системы координат, связанные с минометом и плунжером ГСК - генератора сейсмических колебаний, представлены на рис. 2.

η

Рис.2. Система координат элементов установки ГСК: XYZ – система координат, связанная с минометом; X Z Y – базовая система координат плунжера; £Ц£ - связанная базовая система координат; A x , Л у , A z - координаты центра масс плунжера в базовой системе

где fi_x , в , в — коэффициенты демпфиро-

2C вания по связанным осям,  a0Y =---;

m

С „ С

2       Y2       Z aOY      ; aOZ mm

.

Угловая скорость разворота связанной системы координат относительно базовой может быть представлена в виде

a = ip) + j p + kO .

Уравнение угловых движений по формуле

^^ + ox K = V M

_ dt       ^

где K – кинетический момент:

K = J • a ,

(7) определяется

J =

^ ^J XX

—

J XY

J

XZ

—

—

У

J XY

J XZ

JYY

J ZY

JZ

J zz у

,

Вектор смещения центра масс в связанной системе координат определяется по формуле

^ M - вектор моментов.

Проекции моментов сил на связанные оси

r = i ( A x + A z p ) + j ( Л y -A z p ) + + k ( A z -A x у + A y p ),

будут иметь такой вид:

M _Q = mg A y - C p • p , M n = mg ^{A x -} C p у ,

где p и p - углы поворота связанной системы pq£ относительно базовой системы

M .

= 0 .

С учетом формул (8), (9), (10), (11), (12), (13) получим выражение:

X ^ Z ^ Y . .

Проекция силы тяжести mg на связанные оси может быть представлена в виде

F = - i mg у - j ( mg p) - kmg . (2)

При контакте с минометом сила реакции определяется жесткостью:

F^ = i C_x 8₆ + jC_Y 8_Y + kC_z 8_Z , (3) где C , C , C – коэффициенты жесткости в осях базовой системы координат.

С учетом (2) и (3) получим уравнения поступательного движения:

8x + 2px8x + o2,8x = gу,(4)

Sy + 2P Y 8y + Ю OY 8y = g ф,( 5)

8z + 2p Z 8z + o2z 8z = g,(6)

_T  dp)              d p

J XX --+ Cm ’ p — J XY ---

XX dt      ^p       XY dt

—

• - JxyPp + Jyy • P2 = mgAy, dp

JYY    + Cp ' P  J XY dtdt

• + J XX pp - J xy • P 2 = mg A x ,

—

г dp

XZ dt

—

T dP

JZY ,   JXYpp + dt

+ JYY ' P^ = 0.

Решив уравнения (4) – (6), получим

8 x = C i x exp [ - в + ^

+ ^C 2 X exp ^[ fi x V fi x

+4- • r , ^ OX

-

^a OX ] • t ⁺

®Ox ] t +

-

Sy = C , y exp [ — e Y + №

-

® OY ^]

+ C ₂ y exp ^[- P y ^- ^21

+ g^T- • ^ ,

^ OY

-

^ OY

] • t ⁺

• t +

^S = ^C 1 Z ^{exp [ -} fi z ⁺ 7 fi z - ^ OZ ]■ t ⁺

^C 2 Z ^{exp [ —} fi z - V fi z - ^ OZ ] • t ⁺    2” ,

^OZ где fix > ^OX , Py > ^OY , fiz > ^OZ .

В выражениях (17) – (19) первые два слагаемых при t ^ от обращаются в нуль. Тогда зx = 4g- • V ,                (20)

® OX

g

³ У = —T~ •Ф ,               (21)

® OY

Первый	член	разложения		функции		в ряд
Фурье будет иметь вид
Ф 1 X	= B x	T •	г sin n x I	2 T		(26)
		T	7   Tix   j	2T O
Ф 1 Y	= B y	T	г sin n y i	2 T		(27)
		T	7 п J	, O
Ф 1 Z	= B z	T •	г sin n z i	2 T		(28)
		T	7 n J	, O
где				I
Bx = Bx	gT ^ J xY , J , 7 ^ OX			A y J	,	(29)
B y = By	g^wJ J 2   , ^ , XY , XX , 7 ^ OY			I A x J	,	(30)
B z = B z	s r 2 7 ^ oz J	.				(31)

Тогда уравнение волны для каждой из связанных осей будет таким:

W . = A . B x ,

Sin n x I

--------I ^{, T} , T O n x  J

• 2 п Г

• Sin — I t

T 7

—

x I

I , c J

W n = A n ^By ,

^Sin n y

8 z = 4

® OZ

.

■ 2 п Л

• Sin —I t t 7

—

7 ⁿ J

, T , T o

^y I

I , c J

Уравнения сейсмических волн в системе координат n— примут следующий вид:

д2W 1 д W2

---1 +--7---о =Фх COS дx2    C2 д t2      X

W = A - B z ,

—

x I C J ,

Sin n z I

-------- I ^{, T} , T O n z J

^{д 2} W, .

д У²

£ д W

C2  д t2

_     2 n Г

= Ф _Y cos— t

T I

—

У 1

•  2 n (

• Sin —I t t 7

z

c

I .

д 2 W

----~ + д z ²

1 д W --- = Ф₇

C2  д t2      Z

2 n Г cos— t

T I

c J

,(24)

z Л

—

c J

,(25) где Т – период волны, с – скорость распространения волны.

В результате получаем составляющие поперечных волн    W , , W _n , W _s , которые опре-

деляют несбалансированность плунжера. Для ослабления воздействия поперечных составляющих сейсмической волны проводим статическую и динамическую балансировку ГСК [4, 5], рассчитываем параметры эллипсоида инерции по известной методике [1] и вычисляем углы отклонения главных центральных осей инерции (ГЦОИ) по формулам:

γx

^Jx ² y

^Jx ² z

dp

dw

γ y

\ ^{( J}xx - J yy ) ²    ( J xx — J yy ) ²

J yz

J zz - J yy

^dt t = 0

^dt t = 0

4 = 0 = W| , = 0 = ⁰   (40)

где J , J , J – моменты инерции относительно базовой системы координат,

J , J , J – центробежные моменты инерции.

При установке плунжера в корпусе генератора сейсмических колебаний необходимо развернуть базовые оси плунжера относительно корпуса миномета на угол рассогласования до совмещения ГЦОИ с базовыми осями, при этом плунжер относительно базовых осей OX_ист,OY_ист,OZ_ист занимает положение, в котором вектор виброускорения будет направлен вдоль оси OZ базовой системы координат плунжера и связанной с базовой системой координат ГСК, тогда главные центральные оси плунжера, миномета и корпуса генератора сейсмических колебаний будут совпадать.

Координаты центра масс плунжера Ax = Ay = Az = 0, J_. = JY7 = JV7 = 0, XY    XZ    YZ тогда J примет вид

получим

4 = 0 ,(41)

W = 0 .(42)

С учетом (41), (42) формулы (20), (21) примут вид

Тогда, приняв во внимание (41), (42), (43), (35), получим для составляющих сейсмических волн (32), (33)

W. * 0,(44)

Wn « 0.

Следовательно, составляющая сейсмиче-

ской волны по оси Z будет

B Z

g

V   n z   J

, t , T \

J XX 0 0

^JYY 0

^J ZZ у

Из формулы (16) получаем

J yy W 2 = 0 ,

тогда

.

Уравнения (14), (15) запишем в виде

■  2 п Г.

Таким образом, статическая и динамическая балансировки агрегатов генератора сейсмических колебаний, формирующих динами-

ческие нагрузки, позволяют сохранить одну составляющую сейсмической волны (46), а поперечные составляющие могут быть сведены до уровня функций погрешности баланси-

ровки.

Выводы

Jxxd4+C' 4=0, dt dw.

dt

При начальных условиях

Приведенные результаты исследования не имеют абсолютного характера, их необходимо рассматривать как оценки областей, которым нужно уделять особое внимание при проектировании, построении схем контроля генератора сейсмических колебаний, служащих повышению точности определения координат местонахождения забоя скважин.