Mining wrinkle-patterns with local edge-prototypic pattern (LEPP) descriptor for the recognition of human age-groups

Published Online July 2018 in MECS DOI: 10.5815/ijigsp.2018.07.01

Human age recognition from face image has become an inseparable part of diversified human-centric computing applications, including surveillance monitoring, biometric authentication, and forensic arts [1,

• 2] . However, the task of age recognition is very challenging in practice due to the disparate and complex individual face-aging mechanism [3, 4]. Since human aging can mainly be represented by the aging-affiliated appearance changes on the face, description of these changes is the key to recognize human age. Therefore, detail and fine-point definition of the discernible aging-affiliated textures is required for a reliable agingdescription.

Earlier works on anthropometric studies show that craniofacial growth and skin aging are two common changes that occur during human aging [1], [5]-[8].

Craniofacial growth refers to the gradual shape change in the head skull, while skin aging preserves the texture (appearance) change information associated with skin aging. Our focus is confined to skin aging due to its finer-level texture definition in distinct aging-affiliated patterns, such as, wrinkle, furrow, and blemishes that are considered as significantly visible cues for human aging [9]-[11]. Visually, furrows and blemishes appear similarly as wrinkles; nevertheless, wrinkles appear mostly among these patterns in human faces and become more evident with gradual age progression. Hence, wrinkles are considered as the most discriminative visual cue in human aging [1], [12]-[15]. Motivated by this, we further analyze the appearance of wrinkle patterns in face images more precisely and found that wrinkles mainly appear in two ways, a) strong wrinkles, and b) smoother wrinkles. We also observe that texture-structure of a wrinkle-pixel is significantly different from a nonwrinkle pixel. We argue that incorporating such characteristics of wrinkle patterns in the feature-code is of great importance in recognizing particular age-class. Moreover, subtle intensity distortion may affect the structure of the pixels belonging to a continuing-wrinkle. Therefore, measures should also be taken against such distortion effect in preserving the appropriate structure of the pixels belonging to a continuing wrinkle.

In this work, we address the above issues with the proposed feature descriptor, Local Edge-Prototypic Pattern (LEPP) in order to ensure a reliable description of aging from facial image. We observe that proposed descriptor achieves better accuracy than other existing methods in popular datasets in recognizing human age groups. Moreover, we visualize the comparative efficacy of LEPP against other descriptors under noise, exhibiting the robustness of LEPP in such condition.

• A.    Related Works

Active methods for age recognition can be divided into following categories: anthropometric model [16]-[18], aging manifold model [3],  [19]-[21], deep learning methods [22]-[23], and appearance-based method [14], [24]-[28].

Classical anthropometric models utilize geometric relationships among facial components to represent the facial description. Since facial components are difficult to detect under appearance changes, anthropometric models often end up with low recognition results. Agingmanifold approaches represent face into low-dimensional aging manifolds in embedded subspace. However, these methods are global in nature, and therefore, may lose important micro-level aging information in practice. Recently deep-learning approaches have been applied to age classification task. Most of these methods require additional training data to generate age-model yielding complexity and external dependency to the networkstructure. Moreover, high performance of recent deepmethods is still somewhat dependent on computerhardware. Due to such limitations, there is a growing need for traditional feature descriptors that are fast to compute, memory efficient, and yet exhibiting good discriminability and robustness. Such feature descriptors fall in the category of appearance-based approaches. Roughly speaking, these methods mainly use imagefilters to extract micro-level texture and shape information of face. In particular, there are two directions in appearance-based methods: texture-based descriptor, and edge-based descriptor.

Among texture-based descriptors, Local Binary Pattern (LBP) [24]-[26] is the most popular one. LBP generates code from the intensity difference between a pixel and its neighboring pixels. LBP is advantageous in monotonic illumination but shows sensitivity towards the noise and non-monotonic illuminations  [29]-[30].3  Moreover, because of this naive texture specific coding scheme, LBP code is often inconsistent in capturing the direction of the edge appropriately [27]-[28], which, in turn, makes the LBP code weak in wrinkle patterns, where the edges are most prominent. Conversely, edge-based descriptors such as Positional Ternary Pattern (PTP) [27], Local Directional Pattern (LDP) [29] and Local Directional Pattern (LDN) [30] use the position of top few responses of compass masks to denote the principal axes of the edge, and generate their codes using such edge-directional information. Although edge-based descriptors show their efficacy in preserving the principal direction of wrinkle (e.g., edge) properly, they fail short to preserve many other variations. For instance, owing to using small 3×3 image region, these descriptors gain limited information about the neighboring structure of the target pixel. Therefore, in case of dealing a smoother wrinkle, they often fail to understand the gradual texture change of such wrinkles and misinterpret them as other random textures. Moreover, using such a small region in generating code is prone to subtle noise and local distortion, which may deviate the principal direction-axes and generate different codes. Moreover, except some recent edge-descriptors, such as Directional AgePrimitive Pattern (DAPP) [28], most of the above methods generate codes for featureless textures, such as flat and random noisy textures, arising uncertainty in the feature description. Therefore, roughly speaking, existing descriptors still suffer to incorporate different characteristics of wrinkle patterns unambiguously in representing the age-description, which needs to be addressed properly in order to achieve better agerecognition results.

• B.    Our Contribution

In this paper, we address the aforementioned issues with a new local descriptor, Local Edge-Prototypic Pattern (LEPP), for the age-group recognition problem. The basic idea of LEPP is to set prototypic restrictions for the neighboring pixels using their relation with the center pixel in terms of the gradient information while both of them belong to an edge/line. LEPP uses these restrictions, afterwards, to prioritize the neighbors falling only in the direction of edge within the local neighborhood, ensuring the appropriate shape definition of different patterns, such as wrinkle, furrow, and blemish. Using gradient information allows LEPP to explore bigger neighboring region than that of the former edge-descriptors. This is advantageous to gain richer information of the texture structure, which, in turn, handles slight distortion-affect in local region ensuring consistent structures of the pixels. In this way, LEPP preserves different characteristics of wrinkle-patterns yielding a stable aging-definition. LEPP is found to achieve better performance than other descriptors in benchmark datasets, as well as, it performs well under noise. Hence, the contribution of this work can be summarized as,

• 1)    We present a new local descriptor, Local Edge-Prototypic Pattern (LEPP) that preserves different characteristics of aging-affiliated textures, especially, wrinkles, consistently, yielding a reliable aging-description.

• 2)    We evaluate the stability of LEPP in terms of its robustness to noise, where LEPP is found to perform better than other current descriptors.

• 3)    We evaluate the performance of proposed descriptor on benchmark age-group datasets, where LEPP outperforms existing descriptors convincingly. Moreover, LEPP achieves better accuracy than contemporary deep learning methods at specific case.

• II.    Methodology

Since the aging-affiliated textures, such as wrinkles, blemishes, and furrows mainly appear as edges in the image [14], [27]-[28], characterizing the signature of the edge is crucial in aging description. In our approach, we represent the direction of the inlying edge of a pixel by prioritizing its specific neighbors that form edge/line with the center pixel. For this, we define a set of structural restrictions for the surrounding neighbors. These restrictions are defined based on the prototypic gradient orientation of a neighbor pixel when it forms an edge with the center pixel. We prioritize the neighbors that show such gradient orientations and consider them as the token of the direction of inlying edge. Besides, the neighbors that do not comply with such orientations are ignored. In this way, the proposed coding scheme ensures appropriate representation of the direction of the edge (e.g., wrinkles), and ignores random patterns.

gH = h * i ,                (1)

G V = V * i ,                  (2)

where, H and V are defined as,

"- 1  0    + 1"

H = - 2  0   + 2 ,            (3)

- 1  0    + 1

"- 1   - 2   - 1"

V = 0   0   0.           (4)

+ 1   + 2   + 1

We use G and G to compute gradient magnitude Gi

and gradient orientation O^q of the pixel, i , by

G = 7 ( G H )² + ( G V )²,

a ( G i ) =

G , if , G >  /

0,   otherwise ,

Neighbor Position	Gradient Orientations
	Higher weight, q	Lower Weight, ^	No Weight
0, iv	3,4,11,12	2,5,10,13	Others
I, V	5,6,13,14	4,7,12,15	Others
it, vi	0,15,7,8	1,14,6,9	Others
ui.ru	1,2,9,10	0,3,8,11	Others

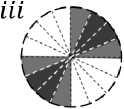
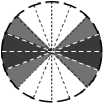
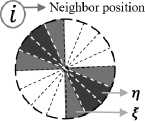
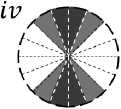
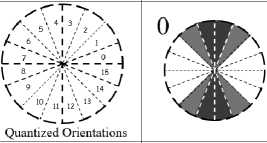
Fig.1. Prototypic-orientations for each neighboring pixel are shown through black and gray colors. Orientations with black and gray colors denote higher (n) and lower weight (f), respectively. Assignment of n and f for each neighbor are also given explicitly in the associated table.

• A.    Coding Scheme

We initiate LEPP code computation by extracting gradient magnitude and orientation at each pixel of an image by applying 3×3 Sobel Operator. Let us denote an image pixel as i. We convolve Horizontal (H) and vertical (V) Sobel operators with that pixel to get corresponding horizontal and vertical edge responses G and G

V

O i = tan ^{- 1}( % ),

where, a(G i ) applies a threshold, y, on the magnitude, G i . This threshold filters the low magnitude of the featureless flat pixels that do not contribute to the representation of edge structure. Gradient magnitudes, that do not pass the threshold, γ, are set to zero, and pixels having such low magnitudes are not considered in the calculation of LEPP code, afterwards. In eq (6), the superscript, q , on orientation, O i , denotes that O i is quantized into q bins. We use q=16 in this work. We now calculate a(G i ) and O^q for all the pixels of an input image.

We characterize the direction of the inlying edge by prioritizing the neighbors that form edge/line with center pixel. When an edge/line is formed between a neighbor pixel and the center pixel, gradient orientation at that neighbor appears orthogonal to the direction of that edge/line [31]-[32]. We regard these orientations as prototypic-orientations of the corresponding neighbors, which are marked by black colors in Fig. 1. In the coding, we impose higher preference to the neighbors showing such orientations, and consider them as the possible directions of the inlying edge. A neighbor usually does not show prototypic-orientations in the absence of an edge/line formed with center pixel, and hence we ignore the neighbors not showing the prototypic-orientation. Formally, we put weights at each kth neighbor based on its orientation Oq as following, respectively,

П , if , O k e { a , b , c , d },

^{e (}O k ) -\^ , if , O k e { p , q , r , s },

0, otherwise, where, β(Oq ) returns higher weight value, η, when Ok directly matches with any of its the predefined prototypic-orientations (a, b, c, d). Besides, orientation appearing in the nearby bins (p, q, r, s) of the prototypic-orientations are assigned slightly lower weight, f. Assignments of n and ffor each neighboring pixel can be found in the table given in Fig. 1. It is noteworthy to mention that we use Gaussian weighting for setting the weight values of n and f. We now prioritize the neighbors by computing priority-score, PSk, at each kth neighbor,

PS

^PS { k :0 < k < 7}

0, if , в ( O k ) - 0,

a(G;J x e(Oq), otherwise, where, PSk only generates scores at the kth neighbor when β(Oq ) is not zero. Thus, eq. (8) generates higher scores in the neighbors those form edge with center pixel. We are interested in n-neighbors having the maximum scores that are to be considered as the major directions of the inlying edge. In the coding, we distinguish these top n-directions by setting bit-1 to their positions, while setting bit-0 to others. Hence, the LEPP code is defined as,

⁷                                      1, a >  0,

LEPPn-ZZk(PSk — PSn)x2k, Zk(a)-^ n    n k-0                                0, a < 0, where PSn is the n-th highest score. Fig. 2 shows an example of LEPP code computation with n=2.

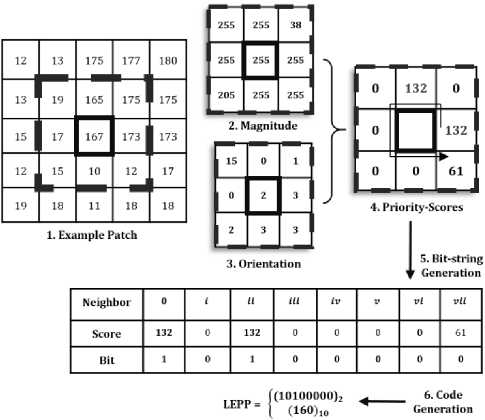
Fig.2. LEPP Code computation (with n = 2 ) for the target pixel, marked in black box in the example patch.

• B.    Feature-vector Generation

We choose histogram-based approach to generate the final feature vector for each face. At each pixel, we compute LEPP code according to eq. (9) and concatenate them into a single histogram to represent a facial description. To incorporate more locality in the code, we divide the image into more blocks ( R¹,R²,…..,R^z ) and generate histogram for each block followed by concatenating them all into one feature vector.

H (k) - Z A (C(x,y),k), A ( a , b ) -| 1’ a = b ’ (10) (x,y) e R ' I ^0, a * ^Ь ,

Ch -^ z 11 H z , (11)

where, C is the LEPP code, k is the number of histogram bin corresponding to a C code of block R^z . Ω is concatenation operator that concatenates each individual histogram, H^z , computed from all z = 1, 2,…,n blocks, and forms single histogram, C H . We regard C H as the final feature-vector in our approach, which we send to the classifier for the classification task.

• C.    Discussion

In this section, we discuss some of the key advantages of the proposed method in preserving diverse variations of aging-affiliated textures.

One key advantage of LEPP is that it represents the structure of the different wrinkle patterns, appropriately. To show this, we provide sample-patches of a stronger and a smoother wrinkle in Fig. 3. Both the wrinkles possess vertical edges, and we observe that LEPP successfully identifies the proper direction of the edges by generating maximum priority-scores at the vertical directions (at position ii and vi ), respectively. This is especially significant for the smoother wrinkles since existing descriptors often misinterpret smoother wrinkles as other random-textures (e.g., flat texture) owing to the inability to characterize the gradual texture-change of such wrinkles. Nevertheless, LEPP explores wider region than that of the other edge-descriptors, and gain richer knowledge of the neighboring structure in order to characterize the gradual texture change information of smoother wrinkles, generating distinctive code for them. In this regard, we also note that LEPP differentiates the textures from featureless flat region. We show such an example in Fig. 3, where we point that LEPP applies a threshold on the magnitude of the pixel in order to filter such texture. Pixels having a lower magnitude (than the threshold), are not taken into account in the codegeneration, afterwards.

Using such wider neighboring information is also advantageous to be more stable against slight distortion and subtle noise-effect in local region. Therefore, LEPP is able to generate consistent code-pattern in the continuing wrinkles. To make it more elaborate, we

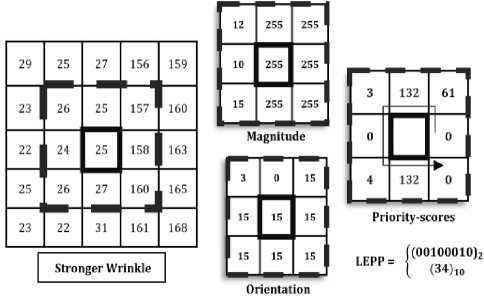
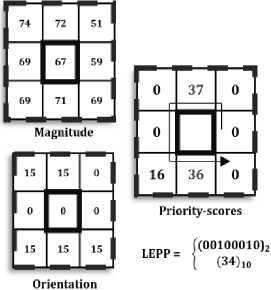
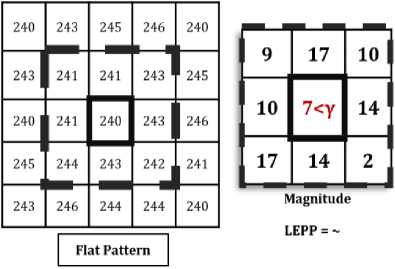
Fig.3. LEPP code for a stronger wrinkle, smoother wrinkle, and a flat patch. We use γ=20 as the threshold.

present an example Fig. 4, where we show the generation of LEPP codes for different parts of a continuing wrinkle. For this, we aim to generate codes at some specific parts of the target wrinkle, where different types of edges are evident, such as diagonal-edge, horizontal-edge, and a curved-edge. We observe that despite having uneven intensity variations around the wrinkle, the diagonal, horizontal, and curved directions are characterized successfully by LEPP, which can be understood by observing maximum priority-scores generated at the diagonal, horizontal and curved positions, respectively. These examples strongly demonstrate the efficacy of LEPP in generating stable wrinkle codes under subtle local distortions.

• III.    Experimental Results

In this section, we present a comprehensive experimental analysis of LEPP regarding its selection of optimal parameters, recognition accuracy in popular datasets, its stability under noise, and its computation time. We perform age-group recognition experiments in three datasets, including, ADIENCE [26], GALLAGHER [33], and FACES dataset [34].

• A.    Experimental Settings

We start our experiment by cropping the face from input images using the given landmark position or manual selection, followed by normalizing it to 110×150 pixels. As described, we divide the face into several uniform non-overlapping blocks and concatenate all the code histograms from these blocks to generate the final feature-vector. For classification, we apply Support Vector Machine (SVM) [35] with RBF kernel function since it has already shown promising result in appearance-based age recognition [27]-[28]. However, to select the optimal parameters, we conduct a grid-search on the hyper-parameters within a cross-validation approach and pick the parameter-values giving the best cross-validation results.

To generate the recognition results for LEPP, we conduct standard 5-fold subject-exclusive crossvalidation experiments, as done in previous works [22], [23], [26], [28]. Subject-exclusive folds are generated in such a way that the folds are disjoint, that is, a subject appearing in one fold does not appear in another fold.

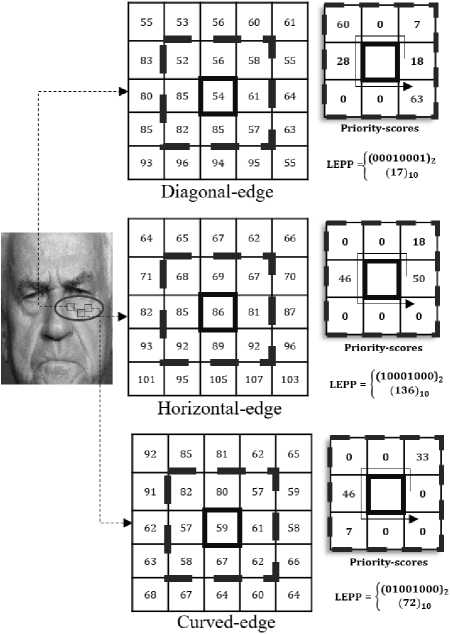
Fig.4. LEPP code in different parts of a wrinkle, especially in a diagonal-edge, a horizontal-edge and a curved-edge.

• B.    ADIENCE Results

ADIENCE [26] is a recently published age-group dataset including both male and female face images within 8 age groups ( 0-2, 4-6, 8-13, 15-20, 25-32, 38-43, 48-53, 60+ ). ADIENCE dataset consists of real-world facial images appearing at significant rotation, expression and pose variations. However, there are two subsets available in this dataset: frontal and complete set. Similar to [26], [28], we conduct experiments on frontal set in this work.

Selection of Optimal Parameters: There are several parameters of the proposed method, such as, threshold γ (in eq. (5)), weight-values for n and f (in eq. (8)), the number of edge-direction n (in eq. (9)), and block-size (in eq. (10)), which need to be set. For the parameter selection purpose, we test the performance of the proposed method for different parameter-values in ADIENCE. The values giving the best recognition rate are selected as the optimal parameters.

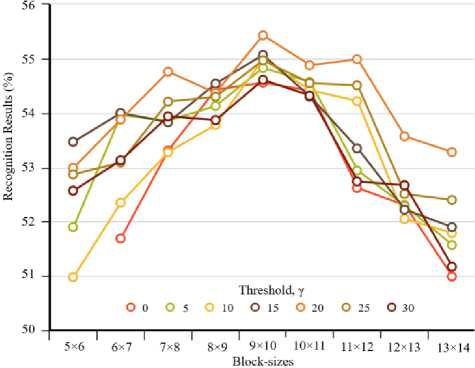
Fig.5. Performance of LEPP for different threshold values and blocksizes in ADIENCE.

At first, we test the performance of LEPP for different γ values varying from 0 to 30 with a stride of 5 within different block sizes varying from 5×6 to 13×14 . The results are shown in Fig. 5. We observe that the highest result is achieved at considering γ = 20 and a block-size of 9×10 . We note that a higher threshold-value may eliminate number of pixels from the image. Therefore, while generating a histogram of a smaller-sized block, one may face lack of samples, causing sampling-error, in practice [36]. Moreover, setting a lower threshold keeps a considerable amount of flat pixels in the face image, which may add redundant information in the feature description. On the contrary, considering comparably larger-sized blocks may possess limited spatial information. Therefore, γ = 20 and block-size of 9×10 gives a good trade-off between preserving sufficient spatial information and adequate samples, and hence we consider these values as the optimal parameters.

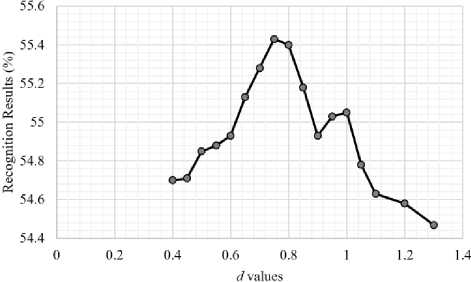
Fig.6. Performance of LEPP in ADIENCE for different standard deviation, d , in setting the Gaussian weight

Moreover, as mentioned earlier, we set the value of η and f through Gaussian weighting with zero-mean and standard deviation, d . That is, different value of standard deviation d can generate different values of n and f. Hence, to select the optimal d value, we test LEPP with different d values ranging from 0.4 to 1.3 . Fig. 6 shows that the highest result is achieved at d=0.75 . However, using d=0.75 with standard Gaussian formula, we get the value of n and f as 0.518612 and 0.240694 , respectively. This means that the higher weight η is almost double of the lower weight f, which appropriately serves our purpose in prioritizing the target neighbors. Therefore, we consider d = 0.75 as the optimal standard deviation value in setting the value of n and f.

Selection of the direction of edge, n, is another important factor in LEPP. For this, we test LEPP for different n values and present the results at Fig. 7, where we observe the highest result at considering n=2 . Considering n=1, LEPP achieves the worst result. However, n=1 points to use only the primary edge direction of the pixel, which may miss the other edge directions that are required for corner and curve-like textures. In this regard, n=2 is more suitable to represent such texture structure with its two edge direction, which is also evident in the results presented at Fig. 6. On the contrary, n=3 is usually appropriate for complex junction-like edge structure. However, the facial image does not possess such complex structure, which why it

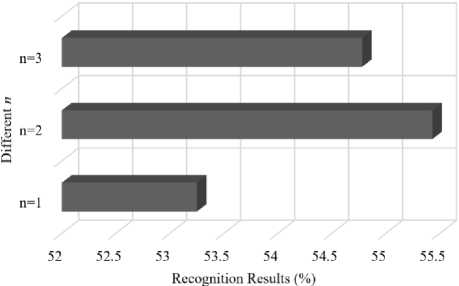
Fig.7. Performance of LEPP for different edge-direction, n , in ADIENCE.

may often add redundant information to the pixel structure, contributing towards its inferior accuracy than that of n=2 . Therefore, we consider n=2 for the optimal n value for LEPP .

Performance under Noise:  We evaluate the performance of LEPP under noisy environment in order to evaluate its stability against such condition. For this purpose, we artificially add random Gaussian noise with zero mean and standard deviation within two intervals (0.08 ~ 0.16 and 0.16 ~ 0.32) for each image of

ADIENCE dataset. It is noteworthy to mention that noises within the given intervals are randomly distributed in order to cope with the uneven natural condition. We now evaluate the recognition accuracy of LEPP against other descriptors, including LBP, LDP, LDN, PTP, and DAPP with 5-fold subject-exclusive cross-validation protocol, and present the results in Table 1. Note that we also present results without adding any noise, in this table. However, for both the cases, proposed descriptor achieves better accuracies than other descriptors, exhibiting its efficacy under such noisy condition. One key reason behind this consistent performance is that LEPP uses larger neighboring area in order to encode the feature-description, which allows LEPP to tackle the effect of subtle noise and distortion of intensity within local texture yielding the generation of stable feature codes. Moreover, some featureless textures, such as flat patterns may change their structure easily under noise. LEPP applies a threshold to filter such uncertain featureless pixels. Therefore, the effect of the uncertain patterns is also limited in LEPP, contributing towards its consistent performance.

Table 1. Performance of Different Descriptors under Noise in ADIENCE dataset

Descriptors	No noise	Noise Variances
		0.08 ~ 0.16	0.16~0.32
LBP	41.1 [26]	31.06	28.98
LDP	48.5 [26]	35.44	32.21
LDN	51.42 [28]	36.35	33.75
PTP	53.27 [28]	39.55	35.87
DAPP	54.9 [28]	40.67	38.64
LEPP	55.43	43.87	40.08

Note: Results with citations are from the original paper

Table 2. Comparative Recognition Results against state-of-the-art Results in ADIENCE dataset with 5-fold subsect exclusive protocol

Methods	Results (%)
LBP [26]	41.1
FPLBP [26]	39.8
LBP+FLBP [26]	44.5
LBP+FPLBP+P0.5 [26]	38.1
LBP+FPLBP+P0.8 [26]	32.9
LBP+FPLBP+D0.5 [26]	44.5
LBP+FPLBP+D0.8 [26]	45.1
LDP [28]	48.5
LDN [28]	51.42
Best from [23]	50.7
Cascaded DCNN [22]	52.88
PTP [28]	53.27
DAPP [28]	54.9
LEPP	55.43

Note: Results with citations are from the original paper

Recognition Accuracy: We test the performance of LEPP in ADIENCE dataset within predefined eight age groups. Table 2 present the results for 5-fold subjectexclusive protocol. Results show that LEPP outperforms the existing descriptors, including LBP, FPLLBP, LDP, LDN, PTP and recently published DAPP. Moreover, it is important to notice that, LEPP performs better than contemporary deep learning methods [22]-[23]. The possible reason behind this better accuracy than the deepmethods is that LEPP preserves the appropriate shape of wrinkle, which enables clear aging definition in the classification. Moreover, LEPP discards the uncertain featureless codes from its feature-vector, which ensures the sole presence of specific aging-affiliated textured code in the histogram. Such explicit representation of aging-affiliated feature perhaps works better than the higher-level features generated by deep learning methods, contributing to the higher accuracy of LEPP.

• C.    GALLAGHER Results

Gallagher dataset [33] consists of a collection of people images with seven age categories: 0-2, 3-7, 8-12, 13-19, 20-36, 37-65, and 66+. Images are collected from various social programs photos, like, wedding, family programs, naïve group photos, etc. GALLAGHER images preserve considerable variability in the images due to the natural face images. For instance, people having dark glasses, face occlusions, and unusual facial expressions can be found in the images, which makes the dataset very challenging in nature.

Table 3. Comparative Recognition Results against state-of-the-art Results in GALLAGHER dataset with 5-fold subsect exclusive protocol

Methods	Results (%)
LBP [26]	58.0
FPLBP [26]	61.0
LBP+FLBP [26]	59.0
LBP+FPLBP+P0.5 [26]	46.8
LBP+FPLBP+P0.8 [26]	41.3
LBP+FPLBP+D0.5 [26]	64.3
LBP+FPLBP+D0.8 [26]	66.6
LDP [28]	66.8
LDN [28]	67.4
PTP [28]	68.8
DAPP [28]	69.91
LEPP	70.44

Note: Results with citations are from the original paper

Table 3 shows the comparative results of LEPP in GALLAGHER dataset. From the presented result, we observe the preeminence of LEPP over existing descriptors. It is important to notice that the results of LEPP are comparatively closer to the edge-based descriptors, such as PTP and DAPP. Nonetheless, the result of LEPP is considerably better than the texturebased approaches like LBP, FPLBP, and their fusions, showing its superiority over such approaches.

However, some of the unsuccessful predictions are given in Fig. 8.

Fig.8. Some unsuccessful predictions from ADIENCE (upper row) and GALLAGHER (lower row) datasets

C. FACES Results

FACES dataset [34] has three image groups: young, middle-aged, and older. Among them, there consists 61 young subjects, 60 middle-aged subject, and 58 older subjects. FACES images are of different varieties, comprising male, female and different expressions. The images were taken under controlled studio environment, and images were carefully post-processed after being taken.

We generate the result for LEPP and other descriptors among three age groups in FACES dataset. We present the results in Table 4, where LEPP shows better performance than LBP, LDP, LDN, PTP, and DAPP. However, it is interesting to note that, LBP performs better than some edge-based descriptors, such as LDP, LDN, and PTP. Perhaps this happens because of the controlled nature of the FACES images, where the effect of noise and uneven illumination are trivial. We also note that the overall recognition accuracies are high in FACES compared to former two datasets owing to the less number of classes in FACES. Moreover, the controlled nature of the face images that avoid the natural deviation of head, lip, and other noise-affect, also contribute towards such overall higher recognition accuracies in FACES dataset. However, the reason for the high accuracy of LEPP than other descriptors in FACES is straightforward. Typically, the older face images possess a high amount of wrinkles. Since LEPP appropriately depicts the wrinkle structure, LEPP feature-histogram contains diverse wrinkle codes. On the contrary, infant and young aged faces possess fewer wrinkles while having more regions that are flat. LEPP explicitly discards the flat patterns in the coding, and hence, infant's faces possess fewer accumulations of wrinkle codes compared to older faces, which clearly differentiates these images from the older one.

Table 4. Comparative Recognition Results in FACES dataset with 5fold subsect exclusive protocol

Methods	Results (%)
LBP	83.3
LDP	82.0
LDN	82.5
PTP	78.31
DAPP	83.43
LEPP	84.25

• D.    Computation Time

  We show the computation time of proposed LEPP in terms of the average time to compute its feature-vector. We conduct this experiment with Visual Studio 2015 on Intel Core i5 @2.67GHz with 8GB RAM. For this experiment, we randomly collect 100 images from the working datasets and record the time required for extracting LEPP feature-vector for each of the images. We compute the average time in milliseconds (ms), and present it in Table 5. We also conduct the same procedure to calculate the computation-time for other descriptors. It is evident that LBP is computationally most efficient method among others owing to its computational simplicity. Edge descriptors, including LDP, LDN, LPTP, and PTP require comparatively more time than LBP due to the convolution process of compass masks. However, proposed LEPP requires slightly more time than more time than the above-mentioned edge-descriptors. For each target pixel, LEPP has to check all the neighbors with its respective structural restrictions, which perhaps consume considerable computation, contributing towards such extra time. However, LEPP still achieves higher accuracy than recently published DAPP, and most importantly, it provides us significant gain in recognition results along with its stable performance under noise. Such stable recognition accuracy, robust performance and moderate computation time strongly advocate the efficacy of LEPP in the recognition of age groups in multi-disciplinary purpose.

Table 5. Feature-vector Computation Time of Different Descriptors

Descriptors	Computation Time (ms)
LBP	3.5
LDP	4.8
LDN	4.6
PTP	4.4
DAPP	6.7
LEPP	6.1

• IV.    conclusion

In this paper, we deal age recognition problem signifying the importance of characterizing diverse wrinkle patterns with consistent feature-codes and propose a new feature descriptor, LEPP, to address this issue. Proposed LEPP descriptor characterizes the inlying edge shape of the pixel by prioritizing the neighbors that form an edge with the center pixel. LEPP initiates a set of structural restrictions to prioritize the neighboring pixels, through which, it avoids the random patterns and represents the appropriate direction of the inlying edge of the wrinkles. Moreover, LEPP uses a wider neighboring area to generate the code, which allows LEPP to be stable against subtle local distortion and noise. We evaluable the performance of LEPP in three benchmark datasets, where LEPP clearly shows its superiority over existing descriptors.

However, extending the proposed coding scheme of LEPP for other facial analysis tasks, such as age estimation, expression and gender recognition, can be regarded as potential future works. We leave these here as our future endeavors.