Minutiae Distances and Orientation Fields Based Thumbprint Identification of Identical Twins

Biometric systems are automated methods of verifying a person on the basis of his physiological and behavioral characteristics. Physiological features based biometrics include iris image, finger prints, thumb print, palm print, face, finger veins, hand geometry, DNA sequence, and palates. Behavioral features based biometrics include gaits (style of walking, and style of talking) signature and voice. Physiological and behavioral characteristics can be used to identify a person if these characteristics satisfy universality, distinctiveness, permanence, and collectability conditions [12].

The twins are classified into two categories namely fraternal twins (monozygotic twins) and identical twins (zygotic twins). Fraternal twins are produced from two eggs and these eggs are fertilized separately by two different sperms. Therefore, fraternal twins differ in face structure, DNA sequence and voice [6]. It is easy to identify fraternal twins on the basis of face structure, DNA sequence, and voice. Identical twins are fertilized from the same egg. Therefore, identical twins have the same DNA sequence and face structure. Identical twins identification is always a challenging task. Identical twins differ in thumbprints (TP), hand geometry (HG), iris images (II), finger veins (FV), palatal structure (PS), finger prints (FP) and gait signatures (GS). Therefore, either one of these biometrics or their combinations can be used for identical twins identification [14][16]. Mathematically, an Identical Twin Identification System (ITIS) can be defined as follow:

(TP, HG, II, FV, PS, FP, GS) ∈ ITIS

ITIS = {TP ^ HG ^ II ^ FV ^ PS ^ FP ^ GS}

If ITIS uses a combination of two or more biometrics for identification then it can be represented as:

ITIS = ^mC n where, 2 ≤ n ≤ m

Here, m represents the total number of biometrics, and n represents the number of biometrics used for identical twins identification.

Figure 1: Facial images of identical twin pair (SatyaPrakash-DevPrakash).

The facial images of an identical twin pair are given in figure 1. The identical twins of figure 1 are sharing same chromosomes and similar physical characteristics. Therefore, they cannot be distinguished using DNA sequence or facial structure. A thumbprint based verification and identification of identical twins was presented by [8]. In verification phase, the system compares an input thumbprint with the enrolled thumbprint of a specific user to determine if they are from the same finger. In identification, the system compares an input fingerprint with the prints of all enrolled users in the database to determine if the person is already known under a duplicate or false identity.

In this research paper we have used a new technique for identifying thumbprint images of identical twins on the basis of minutiae coordinates with orientation angles and minutiae distances.

• II.    RELATED WORK

Identical twins have the closest genetics based relationship. Therefore, the maximum similarities between fingerprints are expected in identical twin pairs. Anil K. Jain showed that a state-of-the-art automatic fingerprint identification system can successfully distinguish identical twin pairs on the basis of their fingerprints with a slightly lower accuracy [6]. Anil K. Jain proposed a new method for identifying identical twins using automatic fingerprint verification system. The system can successfully distinguish identical twins on the basis of minutiae orientation fields. The matching algorithm transforms two minutiae sets to a common frame of reference by using translation and rotation based alignment procedure. Finally, the matching scores are calculated as a function of the number of ‘matched’ and ‘unmatched’ minutiae points [7, 8]. An overview of all biometrics with their advantages and limitations was presented by [9]. A study on evaluating the uniqueness of fingerprints using statistical analysis was presented by [3]. In Han’s method, minutiae points were used for comparing identical twins. Neil Yager proposed minutiae features based personal identification. Minutiae features contain most of the fingerprints individuality and these features are most important for identity verification [18].

A palm print based identical twins identification approach called ‘Competitive Code’ was proposed by [17]. Orientation features based identical twins fingerprint matching method was proposed by [11]. In this method, the fingerprint was divided into non overlapping blocks and representatives of ridges in the blocks were assigned. The orientations of blocks were determined by pixel gradients [11]. Sargur N. Srihari used two levels for identifying identical twins. Six features which are included in level 1 are right loop, left loop, whorl, arch, twin loop and tented arch. Level 2 includes ridge ending and bifurcation features [14]. Tai P. Chen proposed token based fingerprint authentication technique using smart card, USB token, USB thumb drivers, and RFID tokens. Each token contains all the information about fingerprints of an individual [2]. Zhenan Sun proposed a fusion based identical twins identification. In this method, a combination of fingerprints, face and iris image were used for recognizing identical twin pairs [15].

Facial structure based identical twins identification technique was proposed by [10]. Klare used Multi Scale Local Binary Patterns (MSLBP) and Scale Invariant Features Transform (SIFT) descriptors for differentiating identical twins. The multi-scale local binary patterns are the concatenation of local binary patterns feature descriptors with radii 1, 3, 5, and 7 [10]. Soma Biswas proposed a facial recognition based method for identifying identical twins. She described that a human is capable of identifying the discriminations of facial traits which can potentially be useful to develop new algorithms [1]. An efficient technique for identifying individuals using eigen iris, minutiae thumb, and DNA sequence features was developed by [12][13].

Tao X. proposed a new method for finding similarities and dissimilarities between identical and fraternal twins. He observed that similarity between fingerprints of identical twins was 0.7440 where as similarity between fraternal twins was 0.3215 [16].

• III.    PROPOSED METHODOLOGY

The thumbprint patterns of identical twins differ in terms of their minutiae coordinates, orientation angles, and minutiae distances. Therefore, identity of identical twins can be verified by analyzing minutiae coordinates, orientation angles, and minutiae distances of their thumbprints. As per our proposed method, identical twins identification can be carried out using preprocessing, computation, and matching phases.

• A.    Preprocessing

An input image (raw image) is converted to a thinned binary image in preprocessing phase. It also includes following steps for converting thinned input image to a processed image [13]:

Step 1: Image Smoothing [Join the broken ridges of inner parts of a thumbprint image.]

Step 2: Ridge Thinning [Decrease the thickness of ridges to a single pixel value using bwmorph( ) function of MATLAB 7.0.]

Step 3: Black and White Binary Image Conversion [Convert the thinned image to a binary image using im2bw( ) function of MATLAB 7.0]

2(a) satya1

2(b) dev1

2(c) satya2

2(d) dev2

2(e) satya3

2(f) dev3

Figure 2: Thumbprint images of SatyaPrakash and DevPrakash

The thinned binary images of figure 3 are obtained after applying steps 1, 2, and 3 of preprocessing phase on images of figure 2.

A minutia point is a bifurcation point or a ridge breakage point of an image. The methods of finding minutiae points, orientation fields, and minutiae distances are explained in the next section (section III B.)

• B.    Computation of Minutiae Coordinates, Orientation Angles, and Minutiae Distances

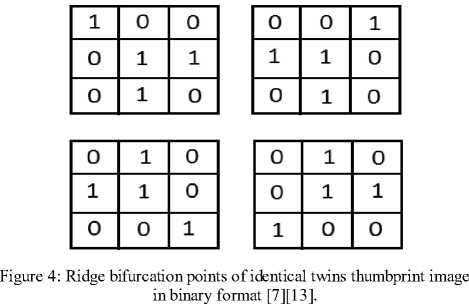
The ridge bifurcation point of a thumbprint image is a point where a ridge bifurcates into two ridges. The binary format of ridge bifurcation points can be represented by figure 4. The ridge bifurcation patterns and the ridge breakage patterns of identical twins thumbprint images can be represented by thirty two different patterns and these patterns are presented in figure 5.

3(a) satya1_thinned

3(b) dev1_thinned

3(c) satya2_thinned

3(d) dev2_thinned

3(e) satya3_thinned

3(f) dev3_thinned

Figure 3: Thinned binary images of SatyaPrakash and DevPrakash.

In figure 5, m1 to m24 are representing ridge bifurcation patterns and m25 to m32 are representing ridge breakage patterns. A minutia point consists of three values: X coordinate, Y coordinate, and orientation angle (θ). The directions of a minutia orientation angle can be categorized into eight parts namely north (N), north_east (NE), east (E), south_east (SE), south (S), south_west (SW), west (W) and north_west (NW).

If each direction of a minutia point is represented by a number then a minutia point and its orientation angle can be represented by following mathematical equations:

Minutia Point = (X, Y, θ);

Where, ө is the angle of orientation of a minutia point.

θ = {N, NE, E, SE, S, SW, W, NW};

Я 6 = {1, 2, 3, 4, 5, 6, 7, 8};                          (3)

Minutia distance matrix is a matrix that represents the distance of every minutia point to every other minutia point in the form of rows and columns. The distance between two minutiae points M 1 and M 2 can be obtained by using following formula:

D 1 = [(x 1 – x 2 )² + (y 1 – y 2 )²]^1/2 (Euclidian Distance)   (4)

Here, (x 1 , y 1 ) and (x 2 , y 2 ) are the coordinates of two minutiae points. D 1 represents the distance between minutiae points. A thumbprint image may have approximately 80 to 150 minutiae points.

0	0	1
L	1	D
0	0	1

0	1	0
0	L	0
1	0	1

1	0	0
0	1	1
1	0	0

1	0	1
0	1	0
0	1	0

• C.    Matching Technique

To find the dissimilarities between thumbprint images of identical twin pairs we need to execute following steps:

Step 1: Store minutiae points coordinates and orientation angles of first person’s thumbprint image of identical twin pair in a matrix M1, where size of matrix M1 is mx3 and m represents number minutiae points.

Step 2: Store the minutiae distances of first person’s thumbprint image of identical twin pair in a matrix M 2 , where size of matrix M 2 is mxm.

Step 3:   Store minutiae points coordinates and orientation angles of second person’s thumbprint image of identical twin pair in a matrix M3, where size of matrix M3 is nx3 and n represents number minutiae points.

Step 4:   Store the minutiae distances of second person’s thumbprint image of identical twin pair in matrix M4 where size of matrix M4 is nxn.

Step 5: Compare M 1 with M 3 and M 2 with M 4 .

if (M 1 != M 3 and M 2 != M 4 )

{ print “Identical Twins have unique thumbprints”;

} else { print “Identical Twins have same thumbprint”;

}

Step 6: END.

m1 = [0,0,1;1,1,0;0,0,1];

m3 = [1,0,0;0,1,1;1,0,0];

m5 = [1,0,0;0,1,1;0,1,0];

m7 = [0,1,0;1,1,0;0,0,1];

m9 = [0,0,0;1,1,1;0,1,0];

m11 = [0,1,0;1,1,1;0,0,0];

m13 = [1,0,1;0,1,0;1,0,0];

m15 = [0,0,1;0,1,0;1,0,1];

m17 = [0,1,0;1,1,1;1,0,0];

m19 = [1,0,0;1,1,1;0,1,0];

m21 = [0,1,0;0,1,1;1,1,0];

m23 = [0,1,1;1,1,0;0,1,0];

m25 = [1,0,0;0,1,0;0,0,0];

m27 = [0,0,1;0,1,0;0,0,0];

m29 = [0,0,0;0,1,0;0,0,1];

m31 = [0,0,0;0,1,0;1,0,0];

m2 = [0,1,0;0,1,0;1,0,1];

m4 = [1,0,1;0,1,0;0,1,0];

m6 = [0,0,1;1,1,0;0,1,0];

m8 = [0,1,0;0,1,1;1,0,0];

m10 = [0,1,0;1,1,0;0,1,0]; m12 = [0,1,0;0,1,1;0,1,0]

m14 = [1,0,1;0,1,0;0,0,1]; m16 = [1,0,0;0,1,0;1,0,1];

m18 = [0,1,0;1,1,1;0,0,1];

m20 = [0,0,1;1,1,1;0,1,0]; m22 = [1,1,0;0,1,1;0,1,0];

m24 = [0,1,0;1,1,0;0,1,1]; m26 = [0,1,0;0,1,0;0,0,0]

m28 = [0,0,0;0,1,1;0,0,0] m30 = [0,0,0;0,1,0;0,1,0]

m32 = [0,0,0;1,1,0;0,0,0]

Figure 5: The ridge bifurcation and breakage patterns of identical twins thumbprint images [4][13].

The next section (section IV) presents experimental analysis of results with actual data of identical twin pair collected by using own scanning device and FVC datasets.

• IV.    EXPERIMENTAL ANALYSIS OF RESULTS WITH ACTUAL DATA OF IDENTICAL TWINS

The thumbprint images of all identical twin pairs can be differentiated on the basis of their minutiae coordinates (X, Y, θ), and minutiae distances.

A. Result Analysis of SatyaPrakash and DevPrakash Images

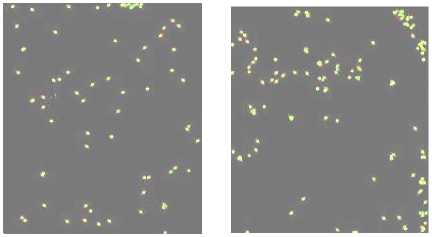
We used MATLAB 7.0 and a desktop computer of 1.7MHz processing speed for conducting experiments. The minutiae points and orientation angles obtained after applying the proposed method on thinned thumbprint images of figure 3 are presented in figure 6. The minutiae coordinates and orientation angles of figure 6 images are calculated using rules of section III..

6(a) dev1       6(b) satya1

6(c) dev2            6(d) satya2

6(e) dev3             6(f) satya3

Figure 6: Minutiae orientation fields of identical twin images

Table I: Comparing thumbprint images of SatyaPrakash and DevPrakash.

I(a) Minutiae coordinates with orientation angles matching%

	dev1	dev2	dev3	satya1	satya2	satya3
dev1	100%	87%	90%	5%	5%	7%
dev2	87%	100%	83%	8%	7%	9%
dev3	90%	83%	100%	6%	6%	6%
satya1	5%	8%	6%	100%	74%	75%
satya2	5%	7%	6%	74%	100%	81%
satya3	7%	11%	7%	75%	81%	100%

I(b) Matching% of minutiae distances

dev1

dev2

dev3

satya1

satya2

satya3

dev1 100% 81% 80.5% 6.2% 6.0% 6.4% dev2 79.5% 100% 82% 6.5% 6.2% 6.1% dev3 80% 81% 100% 6.0% 6.3% 6.1% satya1 6.1% 6.0% 6.2% 100% 84% 79% satya2 6.0% 6.1% 6.1% 82% 100% 79.5% satya3 6.2% 6.1% 6.1% 80% 79% 100% dev1_minutiae_coordinates_and_angles=

{{13,179,2},{14,181,8},{27,178,8},{47,204,2},{49,14,3},{51,207,3}, {53,143,8},{53,208,5},{60,190,4},{60,209,5},{61,203,1},{62,52,6},{ 63,204,4},{66,165,6},{74,43,7},{74,45,8},{86,3,2},{87,210,4},{95,4 6,},{97,138,6},{113,154,6},{117,85,8},{121,90,1},{122,73,2},{123,1 14,},{124,70,4},{133,74,4},{135,150,2},{136,100,1},{146,83,7},{14 9,32,2},{151,30,6},{156,9,3},{160,117,3},{164,213,6},{165,43,7},{1 66,213,5},{170,143,3},{174,115,6},{176,212,6},{182,4,8},{190,27,4 },{192,213,2},{198,56,4},{198,207,6},{217,196,6},{223,208,6},{225 ,178,4},{229,4,4},{230,191,6},{230,202,3},{237,200,4},{239,199,3}, {242,4,2},{244,7,7},{244,182,7},{246,185,7},{246,188,6},{246,198, 3},{247,177,3},{248,172,6},{249,200,4},{251,172,2},{252,180,2},{2 55,123,6},{255,187,4},{258,17,5},{260,29,2},{260,81,3},{261,13,4}, {263,112,4},{263,123,7},{264,13,8},{264,118,3},{264,148,8},{264,1 84,2} };

satya1_minutiae_coordinates_and_angles =

{{3,138,4},{9,80,6},{10,77,7},{10,79,3},{10,85,5},{10,179,4},{11,8 6,8},{12,87,8},{13,75,8},{13,86,4}{13,187,2},{18,108,8},{21,192,3} ,{24,199,2},{26,197,4},{31,16,8},{35,199,8},{38,14,4},{41,22,8},{4 1,156,6},{44,6,5},{47,210,3},{49,30,3},{49,85,8},{50,84,3},{51,85,4 },{53,210,8},{54,210,8},{59,31,2},{60,52,3},{61,142,2},{62,107,6}, {63,28,2},{63,99,5},{64,100,8},{65,99,4},{76,118,2},{68,24,6},{70, 118,4},{71,218,8},{72,134,5},{73,24,5},{74,6,6},{74,53,6},{74,117, 8},{75,86,8},{75,113,7},{77,60,2},{79,104,4},{79,131,5},{79,139,3} ,{79,141,6},{80,99,3},{80,140,4},{81,103,6},{82,48,2},{84,38,4},{8 5,177,7},{91,97,3},{91,106,4},{93,105,3},{109,207,8},{110,25,4},{1 10,40,3},{114,29,5},{115,27,4},{115,183,6},{117,29,3},{121,68,4},{ 122,106,6},{123,69,1},{125,118,3},{132,220,3},{142,190,8},{147,33 ,8},{156,31,4},{157,5,4},{158,209,3},{161,177,7},{162,176,4},{163, 211,5},{164,14,5},{165,13,3},{165,213,4},{165,219,6},{166,15,8},{ 172,216,3},{182,200,4},{188,218,3},{190,206,7},{190,211,3},{200,2 08,2},{208,82,6},{212,217,3},{223,69,6},{223,217,3},{228,184,4},{ 229,154,7},{229,167,8},{236,200,4},{238,209,3},{239,188,3},{243,7 1,5},{244,22,7},{244,49,6},{245,136,2},{245,138,8} };

Figure 7: Numerical representation of minutiae coordinates and orientation angles of dev1 and satya1 images of figure 6.

The numerical representation of minutiae coordinates and orientation angles of dev1 and satya1 images of figure 6 are presented in figure 7. The distances between minutiae points for each image of figure 6 were calculated using Euclidean Distance formula and these distances were compared. While comparing the minutiae coordinates and minutiae distances, the deviations of -10 to 10 were taken into consideration.

The minutiae coordinates with orientation angles and minutiae distances of SatyaPrakash and DevPrakash images were compared using steps of section III C. The average values of minutiae distances and minutiae coordinates with orientation angles were taken into considerations for comparing the thumbprint images of SatyaPrakash and DevPrakash.

The comparison results of DevPrakash and SatyaPrakash thumbprint images are presented in table-I. The ensemble effect of figures 6, 7, and table-I shows that thumbprint images of SatyaPrakash and DevPrakash are not exactly same. The minutiae distances and minutiae coordinates with orientation angles of SatyaPrakash and DevPrakash thumbprint images are completely different.

B. Result Analysis of FVC04 and FVC06 Datasets

We tested the proposed method on thumbprint images of fifty identical twin pairs of Fingerprint Verification Competition (FVC) datasets: FVC04, and FVC06 [4][5]. We selected the most visible image from a set of six to eight images for each person of the twin pair. Few of these images with their minutiae points and orientation angles obtained after applying the rules of sections III A, and III B, of the proposed method are presented in figure 8.

8(a) twin1_p1_image

8(b) twin1_p1_thinned

8(c) twin1_p2_image

8(d) twin1_p2_thinned

8(e) twin2_p1_image

8(f) twin2_p1_thinned

8(g) twin2_p2_image

8(h) twin2_p2_thinned

8(i) twin1_p1_minutiae

8(j) twin1_p2_minutiae

8(k) twin2_p1_minutiae

8(l) twin2_p2_minutiae

Figure 8: Thumbprint images, thinned images, and minutiae points with orientation angles of FVC04 and FVC06 identical twin pairs [4][5].

In figure 8, twin1_p1_image is first person’s thumbprint image of the first twin pair and twin1_p2_image is second person’s thumbprint image of the same twin pair whereas, twin2_p1_image is first person’s thumbprint image of the second twin pair and twin2_p2_image is second person’s thumbprint image of the second twin pair.

The comparison results of figure 8 in terms of minutiae distances, and minutiae coordinates with orientation angles are composed in table II. The analysis of results of table II show that identical twins thumbprint images of FVC04 and FVC06 are differing with each other in terms of minutiae distances, and minutiae coordinates with orientation angles. The ensemble effect of tables II(a) and II(b) prove that identical twins of FVC04 and FVC06 have unique thumbprints.

Out of fifty pairs of identical twins of FVC datasets, the proposed method falsely accepted two pairs and it falsely rejected three pairs of twins. The proposed method is not having any false acceptance or false rejection for DevPrakash and SatyaPrakash thumbprint images. We have observed in experiments that two thumbprint images of the same person of FVC datasets have more than 80% matching score.

Table II: Comparing FVC04 and FVC06 identical twins thumbprint images.

II(a) minutia coordinates with orientation angles matching%

	twin1_p1	twin1_p2	twin2_p1	twin2_p2
twin1_p1	100%	14%	3%	2%

twin1_p2	7%	100%	1%	2%
twin2_p1	2%	1%	100%	13%
twin2_p2	1%	2%	12%	100%

4.	Sun [15]	VeriFinger	EER: 6.79%
5.	Tao [16]	VeriFinger	EER: 5.83%
6.	Proposed	ITIS	EER: 5%

II(b) comparing minutia distance matching%

	twin1_p1	twin1_p2	twin2_p1	twin2_p2
twin1_p1	100%	20%	5%	4%
twin1_p2	10%	100%	2%	7%
twin2_p1	5%	4.0%	100%	18%
twin2_p2	2%	4%	16%	100%

• C. Accuracy and Robustness Testing

For robustness and accuracy testing we deviated each minutiae coordinate of identical twins by ten points in negative and positive sides and then we compared these images at each deviation. The results of DevpPrakash, SatyaPrakash, FVC04, and FVC06 are presented in tables I, and II.

The results of tables I and II prove that images of the same person of identical twin pairs have above 80% matching, whereas the images of two different persons of identical twins have bellow 15% matching. The accuracy comparisons of our proposed method with other methods for measuring the similarities and dissimilarities amongst identical twins thumbprint images in terms of False Acceptance Rate (FAR) or Equal Error Rate (ERR) are given in table III.

The actual images of DevPrakash and SatyaPrakash are ranging from 48KB to 60KB whereas the images of FVC04 and FVC06 are in the range of 105KB to 115KB. As per the proposed method if we store minutiae coordinates and orientation angles of identical twins images for further identification then we need approximately 450 bytes to 600 bytes of memory. If we store minutiae distances of these twins for further identification then we need approximately 11KB to 14KB of memory.

Table III: Comparing the results of our proposed method with other methods.

	Algorithm	Matcher Name	Matching Results (Identical Twins)
1.	Jain [7]	Minutiae	FAR: 2 - 6% higher
2.	Han [3]	Minutiae	EER: 1 – 2% higher
3.	Srihari [14]	NFIS	FAR:6.17%

In worst scenario, if we need to store minutiae coordinates with minutiae orientation angles, and minutiae distances of each person of identical twin pairs in smartcard for further identification then we will need approximately 11.50 KB to 14.50 KB memory space.

V. CONCLUSION

In the proposed method we have found that each person of an identical twin pair has a unique combination of minutiae coordinates, orientation angles, and minutiae distances for the thumbprint images. The proposed method has proved that identical twin pairs have 80% to 95% of dissimilarities in their thumbprints which are better in comparison to the results of other methods discussed in result analysis. The ensemble effect of thumbprints and the essence of sociological behaviors of identical twins can be considered as future research directions in this domain.

ACKNOWLEDGMENTS

The researchers would like to thank Professor (Dr.) Ram Pal Singh (Director, Birla Institute of Technology Ranchi, INDIA - Allahabad Campus) for his kind support in completing this research work. The researchers are thankful to Professor (Dr.) Ajay Chakrabarty (Vice Chancellor, Birla Institute of Technology, Mesra, Ranchi, India) for creating academic and research oriented environment at the institute.