Мягкое декодирование произведений кодов произвольной размерности на базе кодов с единственной проверкой четности

Исследования в области помехоустойчивого кодирования показали достоинства кодов с проверкой на четность (КПЧ), которые наиболее эффективно реализованы в кодах с малой плотностью проверок на четность, в последовательных каскадных конструкциях и в плетеных сверточных кодах [1, 2, 3, 4]. Применение классических конструкций КПЧ с одной проверкой четности в виде произведений нескольких кодов описано в работах [1, 5]. В них особое внимание уделено исследованию кодов размерностей 2D, а коды размерности 3D описаны в работе [6, 7]. Повышенное внимание к подобным системам защиты данных от ошибок объясняется возможностью применения в них простых алгоритмов декодирования, основанных на итеративных преобразованиях индексов мягких решений (ИМР) о принятых символах. Важной особенностью подобных кодов является их структурная приспособленность к использованию в процедуре декодирования перспективных моделей клеточных автоматов [8]. Настоящая работ направлена на распространение возможностей таких моделей на случай, когда конструкция КПЧ составляет размерность 3D и больше.

ПОСТРОЕНИЕ ПРОИЗВЕДЕНИЙ КОДОВ АДАННОЙ РАЗМЕРНОСТИ

Принцип построения произведений кодов (ПК) заданной размерности заключается в сис-

темном изменении избыточности при наращивании объема информационных блоков. Рассмотрим модели построения ПК произвольной размерности. Пусть кодер избыточного кода формирует слова конечной длины n из замкнутого

множества S , для которых справедливо правило единственной проверки четности, применяемое к информационным векторам длины k , тогда n = k + 1 . В общем случае символы этих слов выбираются из конечного алфавита A = { a } , которые приемником фиксируются в виде жестких решений. В общем случае a принимает значения

из GF ( 2 m ) , где m ^G N • Обозначим через

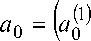
.. a 0^П ’ )

переданную по каналу после-

довательность, а через a s = ( a S 1

,..

., a Sn ⁾ ) ,

S = 1, S другие последовательности рассматриваемого множества. Задача декодера состоит в вычислении функции правдоподобия C 0 для последовательности a 0 такой, что C 0 >  C s для всех последовательностей из S .

Пр

и передаче сигналов a

(О

по каналу с поме-

хами на входе приемника наблюдается вектор w ⁽¹⁾ = W l^ ,—,w nn ⁾ ) = a 0i ^{) +} l ⁽ i ⁾ , где l ⁽ i ⁾ — вектор

шума, компоненты которого – независимые гауссовские величины с нулевым математическим ожиданием и дисперсией N 0 2 . Условная плотность распределения вектора w ⁽ i ⁾ , при m = 1 наблюдаемого на выходе канала, имеет вид

f ( и< ' ⁾ |a 0'⁾) = ( ^N o ) " ¹'² exp !" ( w - £ 1'² ) 2 /N o [ , (1)

где E – энергия сигнала, приходящаяся на один бит.

В общем случае порождающая матрица тривиального КПЧ имеет вид G = [IkxkPkxl ], где Ikxk — единичная матрица, а Pkx1 — единичный вектор-столбец. Для подобного кода при невыполнении условий четности исправление ошибки выражается в инвертировании символа, имеющего наименьший ИМР [1, 8]. Для получения ПК из двух тривиальных КПЧ размерности 2D кодер формирует из k векторов-строк квадратную матрицу a/ = |йхоz||k, где х = 1 ,k, z = 1 ,k и только для данной размерности положим у = 0 . Таким образом, для удобства последующих рассуждений матрица Ak рассматривается в плоскости x0z пространственной системы координат. Матрица Ak путем проверок четности по векторам-строкам и векторам-столбцам преобразуется в матрицу вида An = |йхоz Un • Очевидно, что в Ak общее число информационных элементов достигает значения k2 , тогда как число проверочных разрядов в An будет равно r2d = 2k + 1. Для выявления общих закономерностей формирования избыточных символов ПК произвольной размерности целесообразно значение r2D разделить на две составляющие: r2D = 2k, определяющую избыточность по про веркам информационных разрядов, и V2DD = 1 (проверка проверок) выражающую избыточность для вектора-столбца и вектора-строки. В последующем избыточность, непосредственно зависящую от проверок информационных разрядов, обозначим символом <•> . Проверка от проверочных разрядов представим символом <<•>> . Матричная форма описанного кода имеет вид:

a101    a102   ...   a10k     〈a10n〉 a201    a202   ...   a20k     〈a20n〉

A n =       ........ ..... ..... (2)

a k 01     a k 02     ...   a k 0 k     ^〈 a k 0 n ^〉

〈 a_{n 01}〉 〈 a_{n 02}〉 ... 〈 a_{n 0 k} 〉 〈〈 a_{n 0 n} 〉〉 .

Общая избыточность оценивается выражени ем r2D = r2D + r2D = 2k + 1.

Структура ПК в 3D образуется при у + 0 , если следом за матрицей a x 1 z 1 n по координате y дополнительно разместить новую матрицу II ^ах 2 z I n и так до значения у = n — 1 , а затем на

позиции y = n сформировать матрицу проверок

a xnz 1 n . Следовательно, кодер формирует k матриц A n размерности 2 D , получая совокуп-

ность матриц A n n

a x 1 z

n

, 1

A n

a x 2 z

n

, A n = й_x k _z . Фиксируя х и z , кодер оценивает четность1 выбранных элементов, изменяя y :

^йх1 z ® ^йх 2 z ® ••• ® ^axkz = ^axnz - ^и формирует

матрицу проверок <  A n > = а xnz

n

по всевозмож-

ным x и z . Полученная конструкция в пространстве координат x , y и z образует куб из информационных и проверочных элементов (в общем случае прямоугольный параллелепипед), который назовем кадром. Порождающая матрица этого кода определяется кронекеровским произведением матриц G исходных кодов. Введенная в код избыточность (относительная скорость кода) R оценивается соотношением

DD

R = П 'kq/nq / = П г — V nq / , а минимальное q = 1                q = 1

кодовое расстояние для описанных конструкций

D определяется как dmin = П dq = 2 D .

q = ¹

Применяя последовательно это правило несколько раз, можно получить широкий диапазон длин кодов. Например, код размерности 4D получают из n кадров кода 3D, при этом новые проверочные символы формируют соответствующим сложением одноименных матриц размерности 2D, взятых по одной из всех кадров 3D. Код размерности 4D образуется путем объединения k совокупностей с образованием матричной структуры вида:

A n ¹ =| й х 1 z l n A n ² =| й х 1 z | i n • A 1 k =1 й х 1 z | i n <  A 1 n > = 1 Й Х 1 z| n A 2¹ =| й х 2 z l I n A 2² =| й х 2 z| Щ • A nk =1 й х 2 z| n < A nn >  = 1 й х 2 z l 1^ ...................    .................. ..... ................... .................... (3) k 1          ⁿ       k 2          ⁿ kk ⁿ kn ⁿ

A n H ^ tkz 11       A n H ^ tkz 11      •••     A n H ^ tkz 11       < A n >   f^ k/^ J!

n 1            ⁿ n 2 ⁿ nk ⁿ nn ⁿ

< A n > ^й xnz 11    < A n   > ^й xnz 11     •••   < A n   > |^a xnz 11    <<  A n   >>    ^й xnz 11 •

Необходимо отметить, что в такой конструкции появляется возможность псевдослучайного извлечения матриц 2D из кадров, определяющих информационную совокупность данных разбитых на кадры 3D. В (3) обозначение вида A nij показы- n

1 с номером i из

вает, что берется матрица a xyz

кадра с номером j с образованием проверочных

Таблица 1. Распределение избыточных элементов некоторых произведениях кодов

Размерность кода Значение k Значение n dmin Избыточность по информационным э лемент ам Из бы точн ость п орядка 1 Изб ыточ нос ть п оря дка 2 И збы точн ость п орядка 3 1D k к+1 2 1 0 0 0 2D k2 (к+1)2 22 = 4 2k 1 0 0 3D k3 (к+1)3 23 = 8 3k2 3k 1 0 4D k4 (к+1)4 24 = 16 4k3 6k2 4k 1 5D k5 (к+1)5 25 = 32 5k4 10k3 10k2 5k соотношений вида {•) и {{•)) . Распределение избыточных элементов ПК представлено в табл. 1.

Для произвольных D полная избыточность определяется соотношением

( k + 1 ) D - k^D = ^{f D} ) k^D - 1 + ^{f D} ) k^D - 2 ₊ . „₊^{f D} ) k + 1. (4)

1 1 J       1 ² J           I D - 1 J

Декодер приемника при любой размерности КПЧ обрабатывает только совокупность кадров, поэтому его сложность однозначно определяться сложностью декодирования кадра. Характеристики некоторых ПК представлены в табл. 2. Естественно, код 1D не является произведением кодов, но параметры других кодов, приведенных в этой таблице кратны его k и n . В графе таблицы с символом R ф представлены относительные скорости кодов при условии выкалывания избыточных символов порядка один и более, иначе тех символов, которые определяют структуру избыточных кадров {{•)) .

Анализ показывает, что характеристики приведенных ПК сопоставимы с турбокодами или кодами с малой плотностью проверок на четность [3], но обладают более емким технологическим ресурсом. Например, при организации адаптивных систем обмена данными, при использовании сложных видов модуляции, при реализации принципа выкалывания избыточных данных или в процедуре перемежения составляющих кадров.

ПРОЦЕДУРА ДЕКОДИРОВАНИЯ

НА ОСНОВЕ МОДЕЛИ КЛЕТОЧНОГО АВТОМАТА

Представление КП в виде матриц позволяет использовать в процедуре декодирования достаточно развитый аппарат моделей клеточных ав- томатов (КА). Декодер представляется как бинарный математический объект с дискретным пространством и временем. Для исключения роста сложности декодера КА рассматривается на плоскости, т.е обрабатывает массивы даны в объеме, представленных в (2). Это открывает возможность параллельной обработки подобных массивов данных в плоскостях 0yz , 0xz и 0xy с последующим сведением результатов по принципу декодирования в целом.

При мягком декодировании каждый i-й бит, i = 1 n представляется в виде жесткого решения, сопровождающегося ИМР в виде некоторого вещественногол. , Л = Amin, Amax , определяемого mn max в зависимости от (1) [9, 10]. Обозначая жесткое решение 0 через знак “–”, а решение 1 через “+”, для кортежа двоичных данных …1 0 0 1 1… получают      последовательность вида

... + Л . - л . ₊ 1 - л . ₊ 2 + Л . ₊ з + Л . ₊ 4 ... , которая обрабатывается мягким декодером по правилу:

L<Л„ ) + L(Лpc) - (-1)‘-m хsign[L(Л„ )]х х sign[L (Apc)]х min(L (A„ )|, L (Apc )|)     (5)

где функция sign (•) возвращает знак своего аргумента; L(X ki ) - ИМР символа, участвующего в формировании проверочного бита; L(Л_рс ) -ИМР проверочного символа; m – число исключенных из анализа положительных ИМР, входящих в корректируемый вектор [5]. Применение последнего параметра способствует росту производительности декодера за счет снижения доли неинформативных итераций. Бинарность КА определяется совокупностью знаков “–” и “+”, а диск-

Таблица 2. Параметры произведений кодов ряда размерностей

Размерность кода Значение k Значение n dmin R R Ф 1D 8 9 2 0,89 - 2D 64 81 4 0,79 0,80 3D 512 729 8 0,70 0,73 4D 4096 6561 16 0,62 0,67 5D 32768 59049 32 0,55 0,67 ретные состояния зависят от значений Ai. Правило формирования целочисленных Ai для двоичных видов модуляции определяется выражением

Л ( w ^{) =}

^A max -----A w

PM мп

где M мп – математическое ожидание модулируемого параметра и 0 <  р < 1 - интервал стирания [9]. За конечное число шагов и заданных начальных условиях декодер должен достичь пространственно-однородного состояния, при котором среди элементов матриц будет допустимое число ошибочных. В классическом КА в момент времени t 0 каждая обрабатываемая клетка окружена соседними клетками, находящимися в своих уникальных состояниях. Для оценки состояния произвольной клетки декодера целесообразно использовать определение окрестности клетки по Нейману, которую в данном приложении назовем расширенной. Расширение происходит за счет тех символов, которые определяют выполнение четности для данной строки (столбца). Процедура (5) способствует повышению значения C 0 , но ее исход не является однозначным. Обозначим через (+ pc ) выполнение условия четности на приемной стороне для принятой группы символов. В случае нарушения принципа четности приемник фиксирует значение (— pc ) . Работу декодера с системой итеративных преобразований и проверками на четность целесообразно описывать целевой функцией вида

Q { S;M( A ); г ( A ) } ^ sign ( S )    max min , ₍₇₎

S^(— pc) M(A) Г/Р где S – значение четности по всем информационным разрядам принятой группы символов; параметр ]M (A) - абсолютная величина среднего значения кортежа мягких решений этих символов; параметр <г(А) является показателем разброса мягких решений, вычисляемым по правилу:

гл =n—1)^;.,(м (A)—AD’. (8)

Исследования показали, что по отдельности представленные параметры не являются инфор- мативными и не позволяют оценить очередность обработки нескольких кодовых векторов в системе с произведением кодов [6]. В соответствии с Q{*} декодер на первом шаге декодирования выполняет проверку четности, на втором шаге обработки данных оценивает среднее значение при- нятых ИМР символов и в последнюю очередь определяет степень разброса зафиксированных приемником индексов. Максимальное значение IM (A ) соответствует высокой достоверности принятых символов, однако может быть получено множество одинаковых значений |M (A) при различной совокупности оценок, поэтому допол-

( A ) .

нительно

необходимо оценивать параметр Г

Если возникает ситуация неопределенности, ког- да IMi ЛЪ |M,.(A) при i ^ j , то приоритетной для последующей обработки данных является комбинация, у которой ri (A )< r j (A) .Это полностью отвечает принципу распространения доверия в ходе декодирования группы кодовых комбинаций [6]. Работу декодера рассмотрим на примере обработки матрицы размерности 4х4, параметры которой представлены в табл. 3, при этом в числителе обрабатываемой клетки показаны исходные данные, в знаменателе (выделены жирно) результаты работы декодера.

В каждой матрице 2D имеются сведения о значениях | M ( A ) и <г ( А ) , определенные для всего множества попавших в нее оценок \ A j ^} . Эти данные используются для оценки очередности обработки матриц 2D в составе кадра. В табл. 2 представлен пример обработки клетки с расширенными окрестностями Неймана, однако в ряде случаев горизонтальная или вертикальная со-

Таблица 3. Пример обработки варианта данных матрицы 2D (исходные данные/результат первого шага)

Параметры ^i j A2 j A3 j A pc (pc) IM (A) r(A) Ai, +5 –1 +7 +7 – 5,00 8,00 Ai2 –7 +6 +7 –7 + 6,75 0,25 Ai3 +6 +3 +4 +2/–5 +/– 3,75/4,50 2,92/1,67 Apc –7 –7 +6 +7 + 6,75 0,25 (pc) + + + –/+ 2/2 M (a) 6,25 4,25 6,00 5,75/6,50 5,56/5,75 r(A) 0,92 7,58 2,00 6,25/1,00 3,99/3,13 ставляющие могут отсутствовать, тогда для коррекции данных применяется алгоритм (5).

В примере на основе сравнительных данных для всех Q { • } первоначально обрабатывается столбец с ^ pc . Используя (5), в декодере для выбранного столбца формирует последовательность –7 +2 | +7 (вертикальной чертой выделен проверочный разряд +7, и m = 1 ). После выполнения первого шага итеративных преобразований для выделенной последовательности будет получено

• [ + 2 — 7 ] + 7 = — 5 - новая апостериорная оценка для (-7);

• [ — 7 + 2 ] + 7 = — 5 - новая апостериорная оценка для ( + 2 ) ;

После второго шага итераций

• [ + 2 — 5 ] + 7 = — 3 - вторая апостериорная оценка для (-7);

• [_— 7 _— 5 ] + 7 = - 7 - вторая апостериорная оценка для ( + 2 ) .

Результаты коррекции ИМР столбца:

• + 7 ( —7 — 3 )( +2 — 7 ) + 7 = +7 —10 — 5 + 7 .

Значения индексов больше \Ху | > 7 в блоке заменяются на значение 7 для сохранения разрядной сетки процессора приема при представлении ИМР. Результаты первого шага обработки данных показаны в таблице 3 в виде знаменателей дробей преобразованных данных. Для последующей обработки в соответствии с Q { • } выбирается строка с Лц .

Декодер формирует последовательность +5 -1 | +7 при m = 1 . После первого шага итераций нового цикла будет получено

• [ — 1 + 5 ] + 7 = + 4 - новая апостериорная оценка для (+5);

• [ + 5 — 1 ] + 7 = + 4 - новая апостериорная оценка для ( — 1 ) ;

Второй шаг итерации

• [ — 1 + 4 ] + 7 = + 3 - вторая апостериорная оценка для (+5);

• [ + 5 + 4 ] + 7 = + 7 - вторая апостериорная оценка для ( — 1 ).

Результаты коррекции ИМР первой строки: (+5 + 3)(— 1 + 7) + 7 = +7 + 6 + 7 + 7.

Поскольку для новых данных отрицательные значения для параметра ( pc ) находятся в строке и столбце, необходимо осуществить коррекцию только символа +3, изменив его знак на противоположный. Результат коррекции приведен в табл. 5. Для улучшения общих параметров обрабатываемой матрицы допустимо повышение ИМР символа, находящегося в единственном числе на пересечении строки и столбца.

Подобным образом параллельно обрабатываются другие матрицы 2D. Учитывая однородность данных, одинаковые простые правила перехода и малое число связей между элементами, такие процессы удачно проектируются на архитектуру существующих параллельных вычислительных комплексов. На рис. 1 представлены структуры ошибок, конфигурация которых может возникнуть при обработке матриц 2D. Клетки с серым фоном (номера 1,…, 4) восстанавливаются за счет использования (5) или перекрестных проверок, конфигурации ошибок вида 5, 6 и 7. восстановленными в рамках одной матрицы размерности 2D восстановленными быть не могут.

Оценивается вероятность подобного события сверху для КПЧ 2D выражением вида

P o ^ 2p br ^{х ( 1 —} Р ь ⁾ n ^— 2 ^{х 1} ,     (9)

n                   (n — 1)

где p b – вероятность ошибки на бит.

Таблица 4. Пример обработки варианта данных матрицы 2D (второй шаг/результат второго шага)

Параметры	Л	Л 2 j	Л ; j	Л pc	( Pc )	I м ( Л )	0я
Лп	+5 /+7	–1 /+6	+7	+7	–/+	5,00/ 6,75	8,00/ 0,25
Л 12	–7	+6	+7	–7	+	6,75	0,25
Л 13	+6	+3	+4	–5	–	4,50	1,67
Л РС	–7	–7	+6	+7	+	6,75	0,25
( pc )	+	+/–	+	+	2/ 2
м ( я )	6,25/ 6,75	4,25/ 5,50	6,00	6,50		5,75/ 6,19
^ ( Л )	0,92/ 0,25	7,58/ 3,00	2,00	1,00			3,13/ 1,49

Таблица 5. Итоговые данные

Парам етры	A j	A- 2 j	A 3 j	A pc	( Pc )	| M ( A )	^ ( A )
A	+7	+6	+7	+7	+	6,75	0,25
A 2	–7	+6	+7	–7	+	6,75	0,25
A i3	+6	+/–3	+4	–5	+	4,50	1,67
A	–7	–7	+6	+7	+	6,75	0,25
( pc )	+	+	+	+	2/2
M ( A )	6,75	5,50	6,00	6,50		6,19
^ ( A )	0,25	3,00	2,00	1,00			1,49

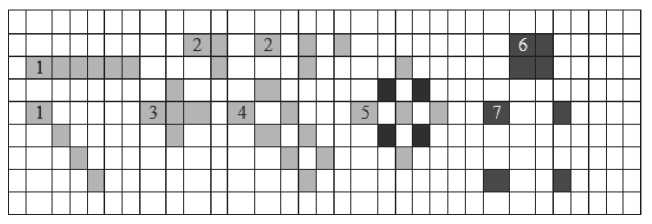
Рис. 1. Структуры ошибочных символов в модели клеточного автомата

ВЫВОДЫ

Применение кодов с единственной проверкой четности в современных системах обмена данными позволяет унифицировать процедуру мягкого декодирования кодовых векторов в составе кодов любой допустимой размерности за счет применения моделей клеточных автоматов, относящихся к NP -полным задачам, и представления кодов в виде наращиваемых по единому принципу для выбранного k конструкций, которые в наибольшей степени приспособлены к современным сетевым технологиям при передаче блоков и ячеек данных.

Открывается возможность параллельной обработки матриц размерности 2D, представляющих кадр данных с последующим сведением отдельных результатов в итоговый результат по принципу декодирования кодового вектора “в целом”. Это в полной мере отвечает организации работы современных процессоров, построенных на ПЛИС.

Анализ выражения (9) показывает, что в условиях низких отношений сигнал-шум вероятность образования невосстанавливаемой структуры ошибок оказывается величиной второго порядка малости. Вероятность образования подобной структуры ошибок в матрице 3D оказывается исчезающее малой, следовательно, невос-станавливаемая структура ошибок в рамках одной матрицы 2D с высокой вероятностью исправляется за счет перекрестных проверок в составе кадра.

Работа выполнена в рамках государственного задания Министерства образования и науки Российской Федерации.