Многоатрибутивное формирование гарантоспособных систем управления и обработки информации

Создание новых и совершенствование существующих систем управления и обработки информации требует решения ряда задач, связанных с формированием структуры систем, а также перечнем функций, которые должны выполнять системы в соответствии с выбранным принципом построения [1; 2].

На сегодняшний день актуальна проблема обеспечения заданного уровня надежности при формировании структуры систем управления и обработки информации с учетом ряда технико-экономических требований [3].

Для обеспечения гарантированной работоспособности систем управления и обработки информации требуется высоконадежное отказоустойчивое функционирование как программных, так и аппаратных средств системы [4]. Реализация механизмов аппаратной и программной отказоустойчивости возможна благодаря использованию программной избыточности и аппаратного резервирования элементов подсистем.

Внедрение дополнительных избыточных элементов в структуру систем управления и обработки информации требует разработки программно-алгоритмических средств формирования оптимального состава систем и планирования оптимального развития структуры систем на различных этапах их жизненного цикла и с учетом динамики функционирования.

Постановка задачи. Рассмотрим систему управления и обработки информации, которая состоит из ряда подсистем. Отказ любой из подсистем приводит к отказу всей системы в целом. Каждая из подсистем может быть реализована несколькими способами, характеризующимися различными значениями параметров надежности, стоимости, ресурсоемкости и т. п. Требуется определить вариант реализации системы управления и обработки информации, т. е. выбрать конфигурацию элементов каждой подсистемы, которая доставляет экстремум некой целевой функции и обеспечивает успешное решение всех задач, поставленных перед системой управления и обработки информации, с вероятностями не ниже заданных ограничений. При этом затраты также не должны превосходить заданных границ.

Метод решения. Математическая модель задачи формирования системы управления и обработки информации имеет следующий вид: определить вариант v0, доставляющий максимум целевой функции

n

P (v) = П j Ujj)(1)

j = 1

при наличии ограничений gp(v) = ZX(uj (ij)) - gP, p=1, -’ q;

j = 1

g p ⁽ v ) = inL g p ⁽ u j (ij > ) ^ g P , p = q ⁺ 1, -, Q ;

j = 1

v G V, Uj(ij) G Uj, j = 1, _, n,(3)

где U j ( i j ) - способ реализации j -й подсистемы; U j = { U j (1), ..., U j ( i j ), ..., U j ( i j ), j = 1, ..., n - совокупность всех элементов, которые могут быть использованы в j -й подсистеме, количество элементов во множестве U j равно £ /' ; v - текущий вариант системы n управления и обработки информации; V = П U j ;

j = 1

P j ( U j ( i j )) - надежность (вероятность безотказной работы на заданном интервале времени) элемента i j -го типа j -й подсистемы; g_p ( U j ( i j )) - значение р -го ограничивающего фактора для элемента i j -го типа j -й подсистемы; g p ( v ) - количество р -го ограничивающего фактора, израсходованного на всю систему; g p * - максимально возможное количество р -го ограничивающего фактора для всей системы в целом.

Задачи (1)-(3) эквивалентны следующей задаче: найти максимум

n f (v) = Z fj( Uj(ij))                  (4)

j = 1

при наличии ограничений (2) и (3), где f j ( U j ( i j )) = = lg P j ( U j ( i j )).

Таким образом, задача оптимального формирования системы управления и обработки информации по критерию надежности сводится к задаче вида (2)-(4).

Если результат решения задачи оптимального формирования неудовлетворителен (т. е. полученная надежность системы управления и обработки информации мала), но используемые ресурсы исчерпаны не полностью, то необходимо прибегнуть к резервированию элементов подсистемы, понимая под этим следующее.

Исследования выполнены в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг.

Если произведено резервирование в j -й подсистеме, и она содержит Л j + 1 элементов (л j резервных и один основной), то выход из строя подсистемы происходит при выходе из строя всех Л j + 1 элементов (так называемое «параллельное резервирование»).

Рассмотрим задачу повышения надежности формируемой системы управления и обработки информации путем резервирования. При этом по мере рассмотрения допустимых значений технико-экономических параметров элементов подсистем будут отсеяны типы элементов, которые учитывать в дальнейшем нет необходимости. В частности, это делается при построении вариантов системы управления и обработки информации с резервированием [5]. Перенумеруем оставшиеся элементы во множествах U j (j' = 1,..., n ) после отсева их по ограничениям (2) и (3), так что U j = { U j (1), ..., U j ( l j ), ..., U j ( £ j )}, где ^ <  ^ (j■ = 1,..., n ).

Для построения вариантов подсистем с резервированием определим максимальный X j ( l j ) и минимальный X j ( l j ) объем избыточности (соответственно, максимальное и минимально возможное число резервных элементов) для l j -го типа j -й подсистемы. При этом будем использовать постоянные для каждой подсистемы величины:

A g p = g p* - g p ( v pv ( I) I U j ), P = 1,..., Q , j = 1, •--, n .

При этом максимальный объем избыточности X j ( l j ) для каждого элемента, вошедшего во множество U j , определим следующим образом:

^х * ₍ у ) = p mm q

^A g^jp ^g P ⁽ u j (lj ) )

где через [ а ] обозначена целая часть а .

Минимальный объем избыточности X j ( l j ) для каждого элемента, вошедшего во множество U j , определяется по формуле

**   _ х у (lj) =

max p=q+1,..., Q

^A g p ^g P ⁽ u j(lj ) )

Несмотря на то что можно положить X**j(lj) = 0, для уменьшения множества возможных вариантов реализации системы управления и обработки инфор- мации с резервированием желательно получить число различных объемов избыточности |Xj(lj)| = X j(lj) -X j(lj) + 1 как можно меньшим.

В случае когда ограничения на минимально допус тимые значения вероятности отсутствуют, минимальный объем избыточности можно определить следующим способом. Будем прибавлять в j-й подсистеме по одному элементу того типа, который имеет максимальную надежность, до тех пор пока при добавлении очередного элемента не произойдет нарушения хотя бы одного из ограничений. Если же ограничения нарушаются сразу, то рассматривается следующий по надежности тип элементов.

Вычислим значение надежности для построенной таким образом системы:

n

P = п (1 - (1 - j U k ( lk ) ))) ^{X k (} ) , k = 1

где P j ( u_k ( l_k )), k ^ j - максимально возможная надежность, которой обладает один из типов элементов, использующийся в k -й подсистеме; P j ( U j ( l j )) - надежность элемента l j -го типа, использующегося в j -й подсистеме; X , ( l j ) - количество резервных элементов l j -го типа j -й подсистемы.

Из выражения P * <  1 - (1 - P j ( U j ( l j ))) X ** ’^(lj )⁺¹ можно определить X ^** j ( lj ) - минимально возможное количество резервных элементов, необходимых для достижения надежности, равной P или более. Ясно, что максимум надежности будет достигаться для величин X j ( lj ) , которые, по крайней мере, не меньше полученных величин X ^** j ( lj ) .

Если определенная таким образом или по формуле (6) минимальная глубина объема избыточности равна X j(у ) хотя бы для одного j = 1,..., n , то максимальный объем избыточности X ^* j ( lj ) , определяемый по формуле (5), может быть уточнен выражением

- *

X j (у) = min p=1,..., q

*

^g p ^   ^{( X} k ( lk ) ⁺ 1) ^g p ^{( U} k ( lk ) )

k=1, k # j gp(Uk (lk))

Видно, что X j(у ) <  X * j(ij ) . Аналогично можно уточнить минимальный объем избыточности, определяемый формулой (6), при помощи известного максимального объема избыточности X ^* j ( lj ) .

Запишем математическую модель задачи оптимального «параллельного» резервирования:

n

P(v) = П Pj(Ujт)) ^ max(7)

j = 1

при наличии ограничений

n gp(v) = Ёgp(UXj)) < g*p, p = 1 -> q, j=1

n gp(v)=Ё gp(u X(lj))) - gp, p=q+1, ->Q, j=1

n

^{X j(lj} )

v 6 V =ПUj,Uj(lj) 6 Uj,j 1 •"’n, j=1

где наличие в варианте системы управления и обработки информации v = ( u^ ^{l l1} ,..., и x j ) ,..., u n-n n^ ) переменной и X j 6 U j означает, что в выбранном варианте в j -й подсистеме в качестве основного и резервных элементов выбраны элементы l j -го типа, и выбранный объем избыточности равен ^X j(lj)^{( X} j(U ) <^X j(lj ) <^X j(lj ) ).

В ограничениях (8) и (10) слагаемые в левых частях, определяющие значение р-го ограничивающего фактора для j-й подсистемы для основного и резервных элементов, примут вид gp (UX'(in)) = (X j(lj) + 1)gp (Uj(lj)) .

Вероятность безотказной работы j-й подсистемы в выражении (7) определяется в виде р (и Xj(ij Л — 1 — П — Р (и    11хj(ij)+I

P j^{( u} j (ij ) ) = ^{1 (i} P j^{( u} j (ij)>>        .

Множество возможных вариантов реализации j-й подсистемы с резервированием имеет вид п" - и.Xj(lj) I -1 F' • А -X**             1

Uj = {uj(ij) 1 lj = 1,-’ ^j’ Xj(ij) = Xj(ij)’-’ Xj(ij)}, j = 1,^, n, число элементов в этом множестве n ξj

। u j i = nz ( x * ( j ) -x j j ) + 2).

j = 1 i j -= i

Представим задачу формирования системы управления и обработки информации следующим образом:

n максимизировать f (v) = ^ fj (uj(tj)) при условиях j=i gp(v) = E gp(u jp) - gp, p =1, ”■> q;

j=i gp(v) =E gp(u j - gp, p=q+1, ”■> Q;

j = i

T n TF7 ^-X j^(lj )

v e V = ПUj,uj(ij) e Uj, j = 1, ..., n, j=i

ξj где Л v) = lgP(v); Uj = {uj(tj) \ tj =1,..., £ (\ X j у,) \ +1)}

—

i j = 1 множество возможных вариантов j -й подсистемы; I Uj = u j и г н V "\.

Эта задача эквивалентна задаче (7)—(I0), поскольку логарифм является монотонным преобразованием. Введение множеств u j является просто результатом замены переменной ujj на uj(tj) с соответствующим изменением множества значений.

Таким образом, имея целевую функцию и ограничения, можно перейти к формированию оптимальной системы управления и обработки информации. Оптимизация происходит по критерию надежности, тогда как на все оставшиеся технико-экономические параметры накладываются ограничения. Ограничение на систему в целом: g p ( v ) - g p ( v ), где p — критерий, на который накладываются ограничения.

Одним из подходов к решению проблемы выбора является следующая итерационная процедура.

Поочередно производится отсев по каждому из критериев. Для этого, рассматривая каждый критерий, для каждой из n подсистем упорядочим все £ j■ типы элементов по возрастанию, согласно значениям рассматриваемого критерия.

Сумма первых значений упорядоченных типов элементов представляет необходимый минимум ресурсов для формирования системы управления и обработки информации. Очевидно, что эта сумма должна быть меньше ограничения на текущий критерий как необходимое условие существования допустимых решений.

Следующим шагом является определение «допуска» для каждой подсистемы, он вычисляется по формуле A g p = g p — g p , где g ps — сумма элементов первого столбца. Все элементы j -й подсистемы, превосходящие значение «допуска», отбрасываются и в дальнейшем уже не рассматриваются. Рассмотрев все критерии, выполняем следующую итерацию.

Процедура заканчивается, когда отсева элементов больше не происходит.

Однако может случиться и так, что все элементы будут отброшены. В этом случае необходимо расширить наложенные на систему ограничения или использовать менее ресурсоемкие элементы в подсистемах.

Резервирование элементов происходит с учетом объема избыточности, что приведет к повышению надежности создаваемой системы управления и обработки информации. Максимизируемая целевая функция будет иметь вид

n

f(v) = Z ( c0lg Pj+ ci), j=i где Pj — надежность j-й подсистемы; с0, сi — константы (с0 > 0), значения которых можно выбрать из соображений удобства вычисления.

Завершающий этап предлагаемого метода — поиск оптимального решения. При нахождении решения используются элементы подсистем с учетом объема избыточности и целевой функции.

Применяется итерационная процедура, предложенная выше. Однако прежде рассмотрения допустимости по критериям рассматривается ограничение на целевую функцию. Это ограничение не задано жестким образом, а находится на каждой итерации по формуле

f ( v ) - f* =

f max + f

*

- i

для первой итерации/и = f _nm, где f „ _ax, f _nm — соответственно сумма максимальных и минимальных для каждой подсистемы значений целевой функции.

Вычисления заканчиваются, когда прекращается отсев, т. е. найдено оптимальное решение, или же когда все элементы какой-либо подсистемы отброшены. Во втором случае приходится расширить ограничение на целевую функцию. Решением будет являться результат, полученный на последней итерации.

Экспериментальная часть. С использованием предложенных подходов и моделей разработана программная система многоатрибутивного выбора компонентов гарантоспособной системы управления и обработки информации. Гарантоспособность системы обеспечивается применением мультиверсионной методологии при реализации отдельных элементов подсистем [6]. Благодаря использованию данной программной системы автоматизируется процесс выбора лучшего варианта реализации гарантоспособной системы из множества предложенных вариантов (рис. i).

	Тараметры системы |S| N£ подсист | Мультиверы-| Стоимость 10бьем     | Время     | Надежность	наде Я		9 1
	1           И            5            10           4            0.6 1             2             17            5             2             0.9 1             3             10            5             5             0.85 1            4            2            40           20           0.55 1             5             5             6             5             0.8 1             6             25            2             2             0.95 1            7            7            35           10           0.65 2             1              8             15            15            0.7 2            2            30           10           10           0.95 2            3            8            10           40           0.75 2            4            10           15           10           0.85 3            1            12           12           20           0.75 3            2            10           15           15           0.7 3            3            25           10           10           0.9 3            4            11           15           38           0.7 4             1              5             5             13            0.7 4            2            4            10           35           0.8 4            3            20           2            5            0.95 4            4            5            6            10           0.8		по объему <= G5 по времени <= 65 Константы СО = 96 С1 =22
			— показать элемент оставшиеся отсев по типам
Исконные данные |"Глубина"| Поиск опт. решения!

Рис. 1. Главное окно программной системы многоатрибутивного выбора компонентов гарантоспособной системы управления и обработки информации

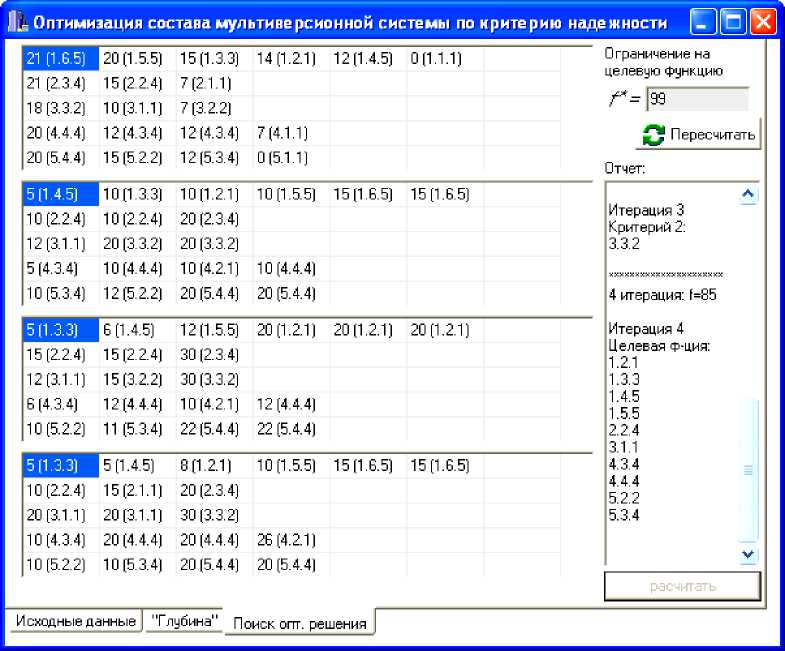
Рис. 2. Выбор компонентов гарантоспособной системы управления и обработки информации с оптимальной избыточностью

Протокол выбора компонентов программной системы многоатрибутивного выбора компонентов гарантоспособной системы управления и обработки информации представлен на рис. 2 в части окна с заголовком «Отчет».

В верхней правой части окна (см. рис. 2) приведено значение надежности формируемой системы управления и обработки информации, которая выступает ограничением при выборе компонентов.

Таким образом, в данной статье выполнена формализация постановки задачи формирования оптимальной структуры системы управления и обработки информации. Согласно данной формализации, при развитии системы управления и обработки информации обеспечивается повышение уровня ее надежности за счет резервирования элементов отдельных подсистем при условии, что ресурсы использованы не полностью.

В результате теоретических исследований, проведенных при тестировании программного комплекса, подтверждена высокая эффективность мультиверси-онной методологии при разработке гарантоспособных систем управления и обработки информации и целесообразность ее применения в таких критичных областях, как космические системы, распределенные вычисления, а также управление и обработка информации.

Результаты работы позволят решать задачи по формированию и развитию структуры систем управления и обработки информации, обеспечивающей гарантоспособность функционирования систем данного класса.