Многофункциональная цифровая модель системы искажения и восстановления изображений

Восстановление изображений часто определяется как процесс оценки исходного изображения по искаженному. Всякий раз, когда точное восстановление невозможно, задача восстановления становится задачей аппроксимации. Задача восстановления обычно формулируется следующим образом: необходимо найти исходное неискаженное изображение z ( x , y ) из уравнения

Az + n = u ( x , y ) + n ( x , y ) = ~ ( x , y ) ,

( x , y ) e W                                     (1)

где A - линейный оператор, n ( x , y ) - шум, ~ ( x , y ) -наблюдаемое искаженное изображение, u e U , и z e Z .

Методы восстановления изображений

Существующие подходы решения задач восстановления изображений условно можно разбить на 3 группы:

• •    подходы, основанные на использовании априорной и апостериорной информации;

• •    подходы, основанные на использовании методов обработки сигналов;

• •    подходы, основанные на методах теории некорректно поставленных задач.

Априорная и апостериорная информация включает в себя ряд параметров, которые учитываются при восстановлении изображений. Апостериорные данные могут быть использованы при определении искажений, которому подверглось изображение при регистрации. Апостериорное знание использует наблюдаемое изображение ~ ( x , y ) для определении некоторого параметра, описывающих искажение. Например, возможно определение функции рассеяния точки (ФРТ) по резким краевым участкам протяженных объектов изображений или по точечным объектам, о которых точно известно, что

они существуют. Другие примеры апостериорных методов включают получение оценок дисперсии шума и спектра мощности из относительно гладких областей искаженного изображения. Иногда, помехи, возникшие при регистрации, становятся очевидными при преобразовании Фурье и эти данные можно использовать в процессе восстановления. Приведенные выше примеры апостериорных методов, конечно не исчерпывают все возможные методы, но они дают представление об основных направлениях в данного подхода.

Большинство методов, разработанных на ранних этапах исследования проблемы обработки изображений, относятся ко второй группе - методам обработки сигналов [1]. Подход, применяемый в задачах обработки сигналов, использует модель с однородным оператором A и функцией рассеяния точки в (1), описываемую выражением:

~( x , y ) =

= JJ h ( x — 5 , y — П ) z ( 5 , П ) dd + n ( x , y ) ’

где ~( x , y ) - зарегистрированное наблюдаемое изображение, h ( x - 5 , y - n ) - функция рассеяния точки, n ( x , y ) - шум и z ( 5 , n ) - искомое, исходное изобра-

жение. Вид уравнения (2) подразумевает, что его вивалентное Фурье-представление может быть писано в следующем виде:

эк за-

U ( f x , f y ) = Z ( f x , f y ) H ( f x , f y ) + N ( f x , f y )  (3)

Известно, что общее линейное решение нения (2) может быть записано как

z ( 5 , n ) = JJ K ( 5 — s , П — t ) ~( s , t ) dsdt где ядро инверсии имеет следующую форму:

K ( s , t ) = -Ay JJ R ( f x , f y ) e ^{i (} s^{fx + tfy} ) df x df y =

4n

н * ( fx , f y ) e i sf x ⁺ t^f y )

д 2 Л I             |2

^{4 П}    HI ( f x , f y )| +^ ( f x , f y )

dfxdf_y ,

урав-

где Т ( f x , f y ) - заданная функция.

Таким образом, при отсутствии шума, очевидный восстанавливающий фильтр – это инверсный фильтр:

R ( f x , f y ) = H ^{- 1}( f x , f y ). (6)

Тогда, z(f, n) может быть найдена путём об- ратного преобразования Фурье выражения:

Z ( f x , f y ) = R ( f x , f y )U ( f x , f y ).               (7)

Однако, обратный фильтр может не существовать, если он имеет экстремумы или H( fy , fy ) не- корректно задан. При наличии шума оптимальный фильтр восстановления (в MSE критериях) это фильтр наименьших квадратов или Винеровский фильтр

R ( fx , f y ) =

H ^*( f x , f y )

H ( f x , f y )²

S nn ( f x , f y ) S zz ( f x , f y )

где S_nn ( f_x , f_y ) и S_zz ( f_x , f_y ) - спектры мощностей шума и исходного изображения, которые мы полагаем известными. Также полагаем, что шум, который был добавлен - это белый шум, то есть, его спектральная плотность постоянна, а изображение и шум некоррелированы. Этот метод хорошо работает для изображений с высоким соотношением сиг-нал/шум, которое определяется как отношение между дисперсией изображения и дисперсией шума, и плохо подходит для изображений с низким соотношением сигнал/шум.

Универсальные методы решения этой проблемы используются в регуляризационном [2-4] и статистическом подходах. В обоих случаях, решение проблемы восстановления состоит в нахождении или условного, или безусловного экстремума, и в частности к поиску минимума следующего функционала:

z = inf M (z )= inf {p (Az, u)+ аф(z)}, (9) z e Z z e Z где Φ(z) является или стабилизатором Ω(z) (в детерминированном подходе), или Гиббсовым потенциалом Γ(z) с α=1 (в статистическом подходе).

К сожалению, при прямом использовании данного метода трудно решить проблему минимизации в общем двумерном случае. Возможность упрощения задачи минимизации обычно базируется на использовании особых свойств интегрального оператора A . Во многих случаях, система отображения описывается однородным оператором, и смазанное изображение определяется уравнением (2). Если искаженное изображение u(x, y) задано на всем участке (x, y)e (-да,да), уравнение (1) является уравнением типа свертки и может быть решено с использованием метода преобразования Фурье. Фактически, искаженное изображение u (x, y) определено на ограниченной области W . Это не позволяет применять преобразование Фурье непосредственно к уравнению (1). Чтобы преодолеть это ограничение, требуется дополнительная процедура, для расширения определения искаженного изображения на весь диапазон (x,y)е(-да,да) [3].

Цифровая модель формирования системы искажения и восстановления изображений.

Эффективное нахождение общего решения задачи восстановления изображений, определенной уравнением (3), представляет собой весьма сложную задачу в том числе и из-за больших размеров изображений и как следствие, большого количества вычислений. Этот недостаток значительно ограничивает широкое использование этого подхода.

Обзор публикаций последних лет показывает, что метод Фурье до сих пор является наиболее широко используемым в задачах восстановления изображений. Хорошо известно, что метод Фурье имеет, по крайней мере, два недостатка: (a) метод применим только для решения уравнений типа свертки и (b) он может использоваться только в линейных алгоритмах восстановления. Для этого случая можно записать:

z „ = inf M ⁽ z ) = inf ^{| Az ^- u |2 + ^a Z |2 ^} .     ⁽¹⁰⁾

z e Z           z e Z              n            z ^y

Использование быстрого преобразования Фурье для решения этой проблемы делает Фурье-подход самым быстрым и дешевым инструментом для решения задачи восстановления. С этой точки зрения, линейные алгоритмы очень важны, поскольку они имеют общую схему основных операций, аналогичную для всех их. Это подобие даёт нам возможность создать многофункциональную цифровую модель процессов искажения/восстановления изображений и использовать ее как основной программный инструмент для разработки, выполнения и сравнения результатов применения этих алгоритмов.

Основные функциональные блоки разработанной модели выполняют следующие процедуры по обработке данных:

• •    Формирование исходного изображения.

• •    Дефокусировка исходного изображения.

• •    Наложение шума на дефокусированное изображение.

• •    Расчет восстанавливающего фильтра.

• •    Восстановление.

• •    Вычисление ошибок.

• •    Визуализация изображений и данных.

Разработанная цифровая модель содержит, наряду с наиболее широко используемыми искажающими функциями, различными видами шума и восстанавливающими фильтрами, набор итеративных алгоритмов для восстановления изображений. Она работает под управлением операционных систем Windows 95/98/NT4/2000 или выше. Взаимодействие пользователя с системой реализовано через графический интерфейс пользователя. Практическое использование разработанной модели продемонстрировано на рисунках 1 и 2.

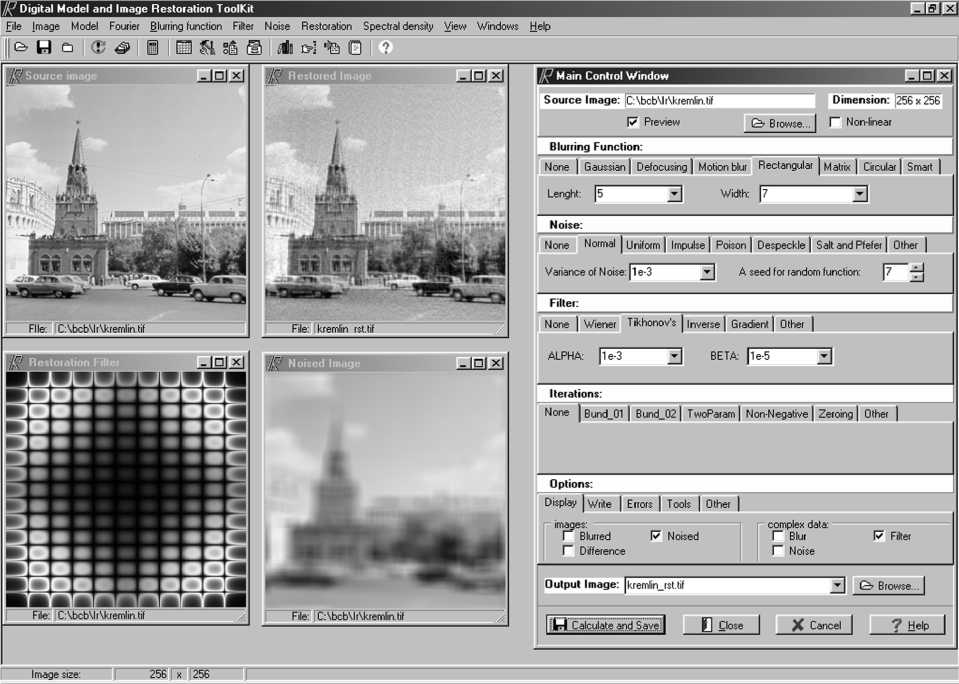
Рис.1. Экран пользователя при использовании Тихоновского фильтра.

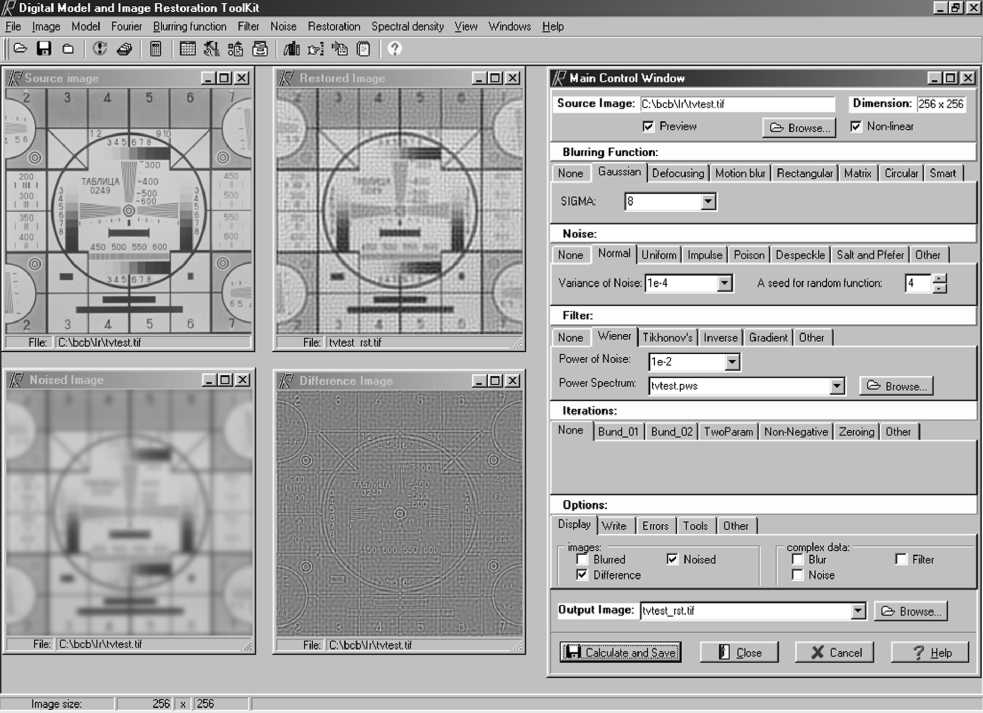
Рис.2 Экран пользователя при использовании Винеровского фильтра.

Обработка данных организована по типу конвейерной обработки. Поток данных обрабатывается последовательно "блок за блоком" со встроенными и программноизменяемыми значениями параметров. Каждый функциональный блок может быть переконфигурирован на этапе выполнения.

На рисунках изображены копии экранов пользователя при работе с моделью. Они содержат несколько графических форм:

• •    Главная управляющая форма модели, расположена на правой стороне экрана. На ней находится семь панелей, расположенных вертикально на форме: "Исходное изображение", "Искажающая функция", "Шум", "Фильтр", "Итерации", "Параметры" и "Выходное изображение".

• •    Другие графические формы используются для необязательной визуализации обрабатываемых данных на разных стадиях процесса обработки изображений.

Рассмотрим главную управляющую форму, представленную на рисунках. Первая и последняя панели используются для выбора исходного и выходного изображений. Пять других сделаны в виде панелей с блокнотами-переключателями. Каждая из них имеет набор закладок, при переключении на которые пользователь получает возможность изменения необходимых параметров. Таким образом, последовательность выбранных пользователем закладок определяет конкретную реализацию модели ис-кажения/восстановления изображения. В частности модель, представленная на рис. 1 определена следующими параметрами:

• •    Искажающая функция определена как прямоугольный смаз; т.е. соответствует прямоугольной ФРТ размером 5х7 пикселов.

• •    Аддитивный шум с дисперсией равной 0.001.

• •    Восстанавливающим фильтром выбран Тихоновский фильтр с α = 1.0 e - 3 и β = 1.0 e - 6 .

• •    Итеративный процесс не применяется.

• •    Смазанное, зашумленное изображение и фильтр восстановления будут визуализированы в процессе обработки данных.

Модель, представленная на рис. 2 определена следующими параметрами:

• •    Искажающая функция определена как Гауссова функция с σ = 6.

• •    Аддитивный шум с дисперсией равной 0.001.

• •    Восстанавливающим фильтром выбран фильтр Винера.

• •    Итеративный процесс не применяется.

• •    Смазанное и зашумленное изображения и разность между восстановленным и исходным неискаженным изображениями будут визуализированы в процессе обработки данных.

Заключение

Разработана многофункциональная цифровая модель системы искажения и восстановления изображений. Модель работает под управлением операционных систем Windows 95/98/2000/NT4.0 или выше. Модель может использоваться как эффективный инструмент для экспериментального выполнения и сравнения различных алгоритмов восстановления изображения основанных на Фурье-подходе. Все необходимые эксперименты в представленной работе были выполнены на этой модели.

Работа поддержана Российским фондом фундаментальных исследований в рамках проекта 9901-39039.