Многоэкспертные бинарные системы как средство повышения вероятностей обнаружения атак на информационные ресурсы

Мир переживает интенсивное развитие искусственного интеллекта, Интернета, вещей (1оТ) и больших данных (big data), бурное развитие Интернета, и поэтому проблема обеспечения безопасности информационных ресурсов становится более актуальной, чем когда-либо. Одним из важнейших инструментов обеспечения информационной безопасности служат системы обнаружения атак (Intrusion Detection System - IDS), которые созданы для наблюдения и фильтрации сетевых действий путем выявления атак, и для предупреждения сетевых администраторов. При создании таких систем широко используется искусственный интеллект [1], машинное обучение [2], искусственные нейронные сети [3], экспертные системы [4-9] и т.д. Комбинированное использование аппарата, искусственных нейронных сетей

и экспертной системы обеспечивает необходимую гибкость и обучение системы на основе новых знаний, в то же время полученные от экспертов знания позволяют улучшить эффективность работы экспертной системы.

В работе [10] была предложена процедура оптимального голосования в многоэкспертных бинарных системах (МЭБС), принимающих только два решения типа да - нет, свой - чужой, атака - нормальное соединение. В основе этой процедуры лежит оптимальный выбор числа экспертов, принимающих положительное решение о наличии той или иной гипотезы. Здесь были рассмотрены два подхода, когда известны условные вероятности принятия решений отдельными экспертами и когда условные вероятности неизвестны, но в экспертной системе возможно проведение режима статистических испытаний. Было показано, что решение системы в режиме статистических испытаний асимптотически приближается к точному решению, когда известны значения условных вероятностей экспертов.

В этой статье процедура оптимального голосования, описанная в [10], применена для оптимизации МЭБС-обнаружения атак типа Reconnaissance (зондирование), экспертами которой выступают многослойные нейронные сети, метод опорных векторов и метод случайного леса. Здесь используется метод статистических испытаний, описанный в [10], который позволяет обойти проблему межэкспертной статистической зависимости.

2.    Постановка задачи и состав базы данных атак UNSW-NB 15

Задача, которая рассматривается в настоящей работе, заключается в создании оптимальной МЭБС-обнаружения атак типа Reconnaissance, основными элементами которой являются многослойные нейронные сети, метод опорных векторов и метод случайного леса.

Обучение и тестирование системы выполнено на современной базе данных UNSW-NB 15 [11]. Подробное описание этой базы данных приведено в работах [12-13]. Эта база данных была создана в 2015 году. В ней были исправлены недостатки баз данных KDD CUP 99 и NSL KDD [14-15], а также были добавлены новые современные виды атак. База данных включает в себя 4 csv файла, содержащих 2540044 записей сетевого соединения. Каждая запись характеризуется 49-ю признаками из пяти категорий: номинальных, целочисленных, числовых, временных и бинарных. Кроме того, имеются также наборы данных для обучения и тестирования, содержащие 175341 и 82332 записей соответственно, число признаков в которых уменьшено до 45. В этой базе содержатся нормальные данные и 9 типов атак [13]:

• •    Normal: нормальные транзакции данных.

• •    Fuzzers: атака на программу или сеть, когда на её вход подаётся большой объём случайно сгенерированных данных.

• •    Analysis: различные атаки путём сканирования портов, отправки спама и текстовых скриптов (HTML файлы).

• •    Backdoors: метод, в котором механизм безопасности системы (аутентификация) обходится незаметно, чтобы получить доступ к компьютеру или его данным, обеспечивая несанкционированный доступ к компьютеру и при этом оставаясь незамеченным.

• •    DoS: вредоносное вторжение, которое делает сервер перегруженным, затрудняя авторизованным пользователям получить доступ к компьютеру.

• •    Exploits: атака, которая использует ошибки в программе или системе, сбои и уязвимости программного обеспечения и приводит к непредвиденному поведению хоста или сети.

• •    Generic: техника, которая работает против всех блочных шифров и использует хеш-функцию, чтобы вызвать коллизию без информации о структуре блочного шифра.

• •    Reconnaissance: атака, которую можно определить как probe - атака, в процессе которой собирается информация о компьютерной сети, чтобы в последствии обойти её защитные системы.

• •    Shellcode: вредоносные программы, где злоумышленник проникает в часть кода для того, чтобы контролировать скомпрометированный компьютер.

• •    Worms: атака, в которой атакующий код копирует себя, чтобы распространиться на другие компьютеры. Часто он использует компьютерную сеть, чтобы распространяться в зависимости от сбоев в безопасности компьютера, который был использован для доступа к сети.

3.    Структуры многоэкспертных бинарных систем 3.1.    Структура многоэкспертной бинарной системы, состоящей из трех экспертов

Как отмечалось во введении, в настоящей статье процедура оптимального голосования, описанная в [10], применена для оптимизации многоэкспертной бинарной системы обнаружения атак типа Reconnaissance, поскольку количество атак этого типа занимает серединное положение среди числа атак, представленных в базе данных UNSW-NB 15. Для краткости в дальнейшем атаку типа Reconnaissance будем обозначать как атака R. Предварительно данные базы UNSW-NB 15 проходят предобработку, т.к. в том виде, в каком они представлены в базе данных, не могут непосредственно использоваться в многоэкспертной бинарной системе. Структура предобработки данных показана на рис. 1.

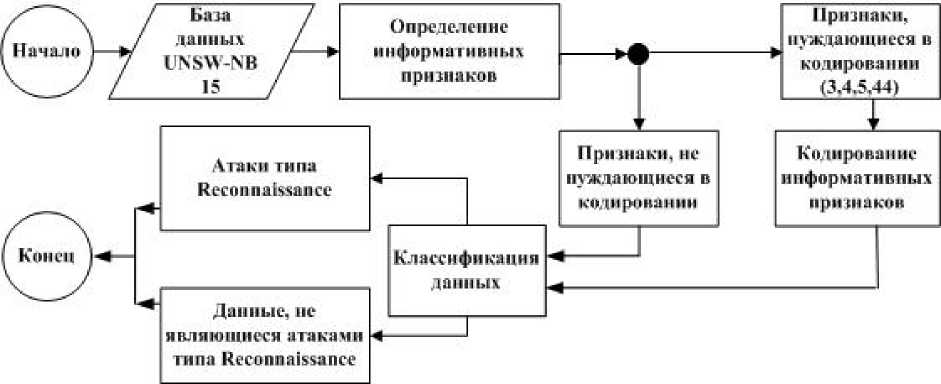
Рис. 1. Структура, предобработки данных базы UNSW-NB 15

В соответствии с этой структурой анализируются признаки данных из базы UNSW-NB 15, после чего нечисловые признаки 3, 4, 5 и 44 кодируются, и все данные разделяются на. два. класса: данные, соответствующие атакам типа. Reconnaissance (атака. R) и остальные данные, состоящие из нормальных соединений и всех типов атак кроме атак R, которые далее будут называться «не R атаки».

Для создания МЭБС в задаче обнаружения атак в качестве экспертов в настоящей статье использованы эксперты на. основе многослойных нейронных сетей (МНС) [16], метода, опорных векторов (SVM - support vector machine) [16] и метода случайного леса (RF -random forest) [17]. Ниже рассмотрены две структуры таких систем, одна, из которых состоит из трех бинарных экспертов в виде 3-х МНС, а другая - из 5-и бинарных экспертов, 3 из которых МНС, а. также SVM и RF.

Данные из предобработанного набора данных из базы данных UNSW-NB 15 разбиваются на обучающую и тестовую выборку. Обучающая выборка содержит 80% данных, а тестовая - оставшиеся 20%. В свою очередь, обучающая выборка разбивается на три равные части для обучения каждого эксперта. Оценка, результатов обучения производится с помощью тестовой выборки. Состав данных файлов обучения и тестирования представлен в табл. 1. Структура. МЭБС, состоящей из 3-х экспертов, представлена, на. рис. 2.

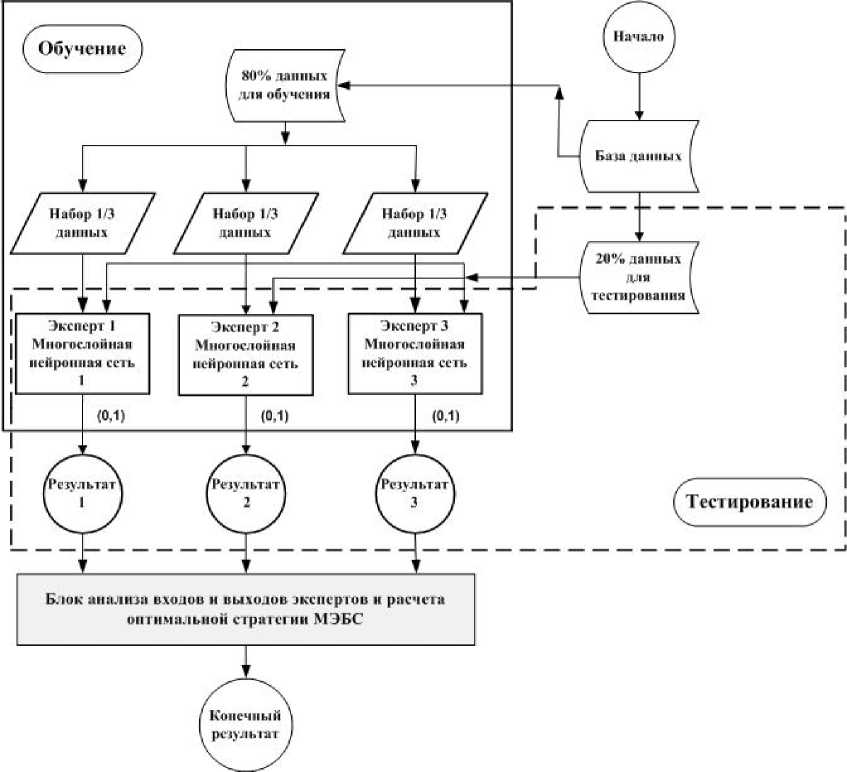
Рис. 2. Структура. МЭБС, состоящей из 3-х экспертов

Таблица. 1

Состав данных файлов обучения и тестирования для трех экспертов

	Количество атак типа R	Количество данных остальных типов (не R атак)
Состав файла обучения для 1-го эксперта	2725	40897
Состав файла обучения для 2-го эксперта	2725	40900
Состав файла обучения для 3-го эксперта	2723	40874
Состав файла тестирования для МЭБС, состоящей из трех экспертов	2043	30727

Для повышения точности обучения в каждом файле обучения методом повтора, количество атак R сделано равным количеству не R атак. МЭБС построена на базе нейронных сетей, при этом каждый эксперт представлен МНС, но с разным числом нейронов и слоев, характеристики которых приведены в разделе 4.1 Обучение и тестирование экспертов МЭБС.

3.2.    Структура многоэкспертной бинарной системы, состоящей из пяти экспертов

Структура. МЭБС, состоящей из пяти экспертов, представлена, на. рис. 3.

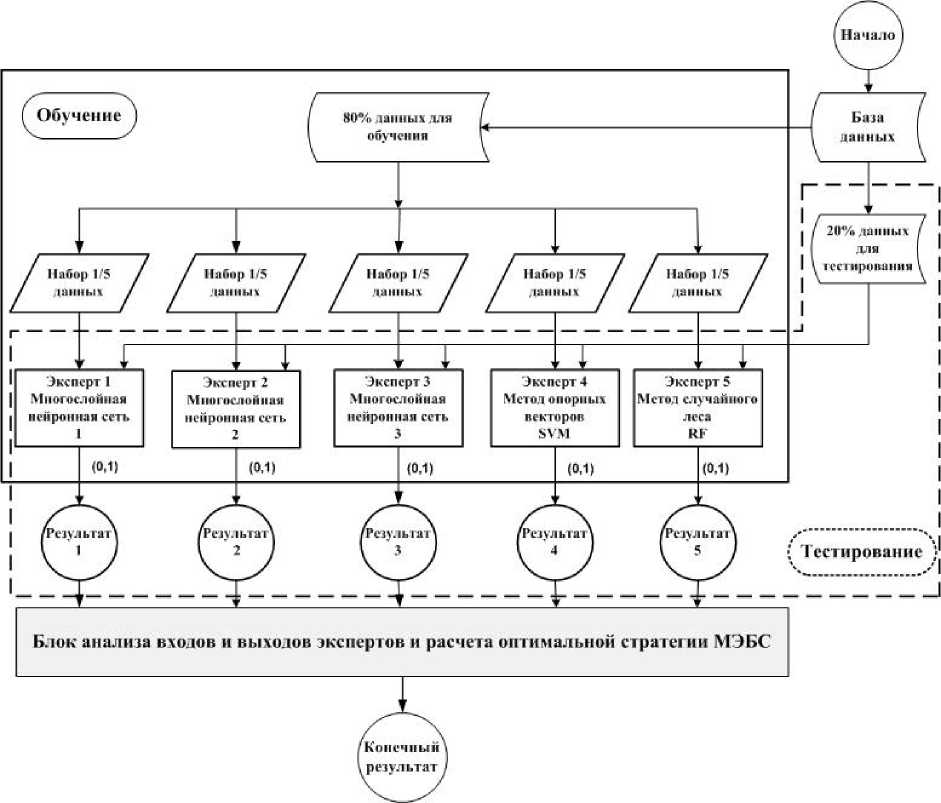
Рис. 3. Структура. МЭБС, состоящей из пяти экспертов

Эта. система, представляет расширенную версию предыдущей системы, в которую добавлены два. эксперта, в виде метода, опорных векторов и случайного леса. Как и для случая трех экспертов, здесв для повышения точности обучения в каждом файле обучения методом повтора, количество атак R равно количеству не R атак. Обучающая выборка. из 80% данных разбивается на пять равных частей для обучения каждого эксперта. В табл. 2 указаны состав данных для обучения и тестирования каждого эксперта.

Таблица. 2

Состав данных файлов обучения и тестирования для пяти экспертов

	Количество атак типа R	Количество данных остальных типов (не R атак)
Состав файла обучения для 1-го эксперта	1634	24544
Состав файла обучения для 2-го эксперта	1634	24545
Состав файла обучения для 3-го эксперта	1634	24539
Состав файла обучения для 4-го эксперта	1634	24540
Состав файла обучения для 5-го эксперта	1637	24555
Состав файла тестирования для МЭБС, состоящей из 5-и экспертов	2043	30727

Обучение МЭБС выполняется в два этапа. На первом этапе по доступным для обучения данным происходит обучение всех экспертов системы распознаванию конкретного вида атаки. На втором этапе обученные эксперты интегрируются в МЭБС, которая в зависимости от решения каждого эксперта в соответствии с соответствующим ей алгоритмом принимает решение о характере входного сигнала: атака R или не R атака.

4.    Экспериментальные результаты4.1.    Обучение и тестирование экспертов МЭБС

Обучение экспертов МЭБС выполняется по данным, представленным в табл. 1 и 2, с помощью пакета прикладных программ Neural Network Toolbox, входящего в состав MATLAB Application Toolboxes так, чтобы достигнуть наилучшего результата обучения каждого эксперта.

В случае МЭБС, состоящей из трех экспертов МНС, было проведено обучение и тестирование трехслойных (15-10-1, 30-20-1, 50-30-1, 100-50-1, 100-100-1, 150-100-1, 200-100-1, 200-150-1) и четырехслойной нейронной сети (30-20-10-1), где первая цифра - число нейронов в первом слое, по данным, числовые характеристики которых представлены в табл. 1. Число входов как в МНС, так и в SVM и в RF равно числу информативных признаков в записи сетевого соединения, равное 42. У всех МНС в последнем слое находится один нейрон с аналоговым выходом. В режиме тестирования и последующего функционирования выходной сигнал обученной МНС поступает на пороговый элемент, принимающий значения 0 (не R атака) и 1 (атака R) в зависимости от значения его порога. Значение порога существенно влияет на вероятности обнаружения как не R атаки, так и атаки R и выполняет важную функцию последующей оптимизации МЭБС. С этой целью величина порога реализована как переменная величина, которая принимает различные значения от 0.1 до 0.9 с шагом 0.01.

При обучении МНС был использован алгоритм обучения Левенберга-Марквардта (trainlm) [18]. Среди обученных и тестированных МНС для включения их в состав МЭБС были выбраны три, которые характеризуются наилучшими параметрами обнаружения атаки типа R и не R атаки.

В случае МЭБС, состоящей из пяти экспертов в составе трех МНС, SVM и RF, было проведено обучение и тестирование по данным, числовые характеристики которых представлены в табл. 2. МНС обучались по процедуре, аналогичной описанной выше для случая трех экспертов. Обучение эксперта по методу опорных векторов (SVM) выполнялось при различных значениях функций ядра [19]: Gaussian Radial Basis Function (RBF), linear, polynomial. Эксперт по методу случайного леса, который базируется на ансамбле из большого числа решающих деревьев [20], использовал подвыборку размером N, где N = 42 -число информативных признаков сетевого соединения. Среди обученных пяти экспертов для включения их в состав МЭБС были выбраны те, которым соответствуют наилучшие характеристики обнаружения атаки R и остальных соединений, табл. 4.

Таблица 3

Параметры трех экспертов

№ эксперта	Параметры
	Тип эксперта	Метод обучения	Число слоев и нейронов в слоях	Порог	Процент обнаружения атак R, %	Процент обнаружения не R атак, %
Эксперт 1	МНС	Trainlm	30-20-10-1	0.74	73.86	96.41
Эксперт 2	МНС	Trainlm	30-20-1	0.74	85.12	94.32
Эксперт 3	МНС	Trainlm	15-10-1	0.74	90.70	93.91

Таблица 4

Параметры пяти экспертов

№ эксперта	Параметры
	Тип эксперта	Метод обучения	Число слоев и нейронов в слоях	Порог	Процент обнаружения атак R, %	Процент обнаружения не R атак, %
Эксперт 1	МНС	Trainlm	30-20-10-1	0.6	84.68	92.39
Эксперт 2	МНС	Trainlm	30-20-1	0.6	80.52	94.08
Эксперт 3	МНС	Trainlm	15-10-1	0.6	89.92	94.33
Эксперт 4	SVM	Rbf	-	-	88.06	90.86
Эксперт 5	RF	All	-		87,66	93.37

4.2.    Процесс оптимизации МЭБС для повышения вероятности обнаружения атак R

МЭБС предназначена для такого объединения результатов решений отдельных экспертов, чтобы решение многоэкспертной бинарной системы было лучше, чем решения отдельных экспертов. Подходы к решению этой задачи и соответствующие алгоритмы можно найти в работах [21-24]. В [10] была описана и исследована процедура построения оптимальных МЭБС, которая расширила метод голосования по большинству - один из основных методов МЭБС. Метод голосования по большинству предполагает, что МЭБС принимает решение о конкретной гипотезе, если за данную гипотезу проголосовала более половины экспертов. В [10] показано, что этот подход интеграции решений экспертов не является наилучшим: необходимо исследовать все возможные решения МЭБС, состоящей из К экспертов, когда конкретная гипотеза принимается, если за нее проголосовали более М экспертов. Число таких решений равно числу экспертов К и среди этих решений существует одно решения голосования по большинству. Оптимальным решением МЭБС будет одно из К решений системы, при котором функционал системы достигает оптимальное значение.

Расчет данных решений МЭБС может быть выполнен при известных вероятностях правильных решений экспертов системы в случае, когда решения отдельных экспертов статистически независимы. В случае статистической зависимости в [10] предложена процедура, которая основана на методе статистических испытаний и которая позволяет обойти проблему статистической зависимости решений отдельных экспертов.

В настоящей работе для оптимизации МЭБС использован метод статистических испытаний, несмотря на то, что вероятности решений экспертов были предварительно оценены. Причина тому - статистическая зависимость экспертов, которая не была полностью устранена обучением экспертов на различных данных.

Оптимизация МЭБС, состоящей из трех экспертов

В случае применения принципа голосования по большинству система сообщает об обнаружении атаки R, если два или три эксперта сообщают, что происходит атака. Если же два или три эксперта сообщают, что имеет место не R атака, то система сообщает, что атака R отсутствует имеет место не R атака. При таком подходе распознается 85.71 % атак типа Reconnaissance и 95.06% случаев остальных соединений.

Оптимизация МЭБС голосования выполнена путем изменения принципа голосования следующим образом: если три эксперта голосуют, что имеет место не R атака, то система сообщает об отсутствии атаки R, в остальных случаях система сообщает об обнаружении атаки R. Результат для такой системы: распознается 96.23% атак R и 91.07% случаев остальных соединений.

Кроме этих двух возможных решений МЭБС, существует и третве, когда атака принимается, если за нее голосуют три эксперта. Все три возможных решения для данной системы представлены в табл. 5.

Решения МЭБС, состоящей из 3-х экспертов

Таблица 5

№ решения		Число атак в выборке	Число не R атак в выборке	Число не R атак, принятых за атаку R	Число обнаруженных атак R	Процент обнаруженных атак R, %	Процент обнаруженных не R атак, %
1	3 эксперта сообщают о не R атаке	2043	30727	2744	1966	96.23	91.07
2	2 или 3 эксперта сообщают о не R атаке	2043	30727	1519	1751	85.71	95.06
3	1, 2 или 3 эксперта сообщат о не R атаке	2043	30727	459	1384	67.74	98.51

Экспертная система может выбрать одно из трех возможных решений согласно с заложенным в ней критерием, например [10]. Если система принимает решение в соответствии с первой строкой табл. 5, то она дает предпочтение обнаружению атаки R. Если система принимает решение, соответствующее третьей строке, предпочтение дается обнаружению не R атак. Заметим, что вторая строка соответствует принципу голосования по большинству. На рис. 4 приведено сравнение принципа голосования по большинству и решения, которое представлено в первой строке табл. 5.

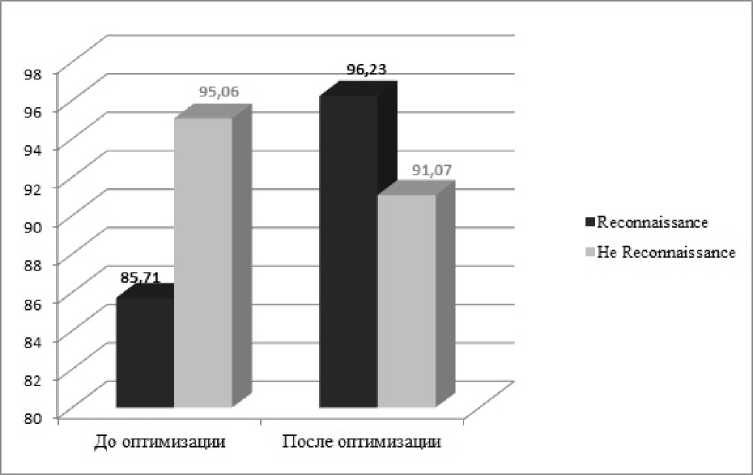
Рис. 4. Сравнение результатов до оптимизации и после оптимизации (принцип голосования по большинству и решение первой строки табл. 5)

Процесс оптимизация МЭБС, состоящей из пяти экспертов

В [10] было показано, что увеличение числа независимых экспертов в МЭБС приводит к повышению вероятности правильного решения о наличии той или иной гипотезы. Настоящий эксперимент с пятвто экспертами должен был подтвердить или опровергнуть этот вывод для случая статистической зависимости между экспертами в модельной задаче обнаружения атак типа R и не R атак. В табл. 6 приведены результаты 5 возможных решений МЭБС, состоящей из пяти экспертов.

Таблица б

5 решений МЭБС, состоящей из пяти экспертов

№ решения		Число атак в выборке	Число не R атак в выборке	Число не R атак, принятых за атаку R	Число обнаруженных атак R	Процент обнаруженных атак R %	Процент обнаруженных не R атак, %
1	5 экспертов сообщают о не R атаке	2043	30727	3868	2018	98.78	87.41
2	4 или 5 экспертов сообщают о не R атаке	2043	30727	2699	1983	97.06	91.22
3	3, 4 или 5 экспертов сообщают о не R атаке	2043	30727	2195	1871	91.58	92.86
4	2,3,4 или 5 экспертов сообщают о не R атаке	2043	30727	1497	1629	79.74	95.13
5	1,2,3,4 или 5 экспертов сообщают о не R атаке	2043	30727	490	1301	63.68	98.41

Из анализа табл. 6 следует, что оптимальная МЭБС с пятью экспертами предоставляет возможность в выборе того варианта решения, который позволит решить задачу обнаружения атаки R или не R атаки в соответствии с функционалом, который заложен в систему. В отличие от системы голосования по большинству, представленной третьей строкой таблицы б, с вероятностью обнаружения атаки R, равной 0.92, и вероятностью обнаружения не R атаки, равной 0.93, данная система предоставляет еще 4 варианта решений, которые могут быть использованы согласно заложенному в систему функционалу.

Результаты, приведенные в табл, б, показывают, что система с большим числом экспертов (5) более успешна, чем система с меньшим числом (3). Достаточно сравнить первую строчку табл. 5 и вторую строчку табл. б. Результаты данного сравнения представлены на рис. 5. Обе вероятности для МЭБС, содержащей 5 экспертов, больше соответствующих вероятностей системы с тремя экспертами.

Представленный в настоящей работе подход к оптимизации МЭБС позволил получить результаты, которые существенно лучше известных результатов. Так, в работе [25] сообщается о 69.9% процентах обнаружения атак типа Reconnaissance, а в работе [26] - о 75.26%.

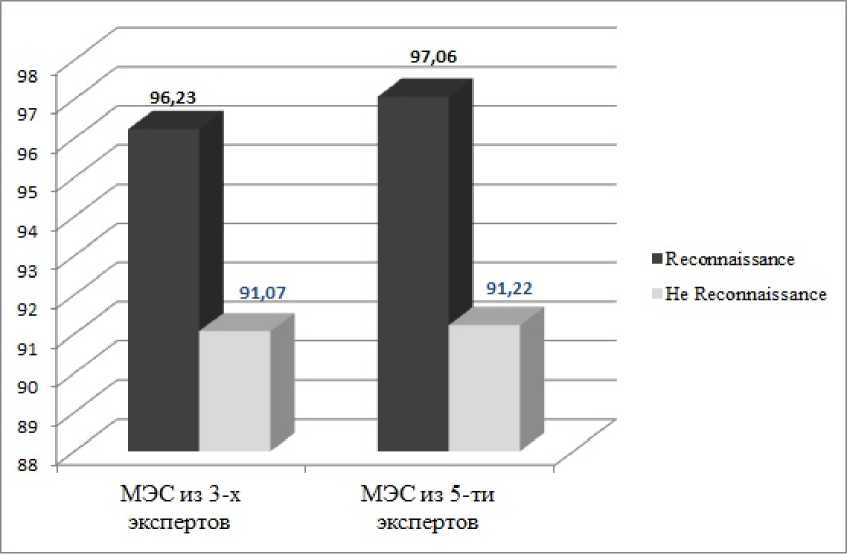
Рис. 5. Сравнение результатов многоэкспертных бинарных систем, состоящих из трех и пяти экспертов

5.    Заключение

Приведенные результаты применительно к задаче обнаружения атак типа Reconnaissance показывают, что оптимальные МЭБС могут служить эффективным инструментом, позволяющим повысить вероятность обнаружения атак. Данный подход может быть применен к различным видам атак.

Повышение вероятностей обнаружения атак и других соединений в МЭБС может быть выполнено за счет повышения числа экспертов системы и обеспечения максимально возможной статистической независимости экспертов. Последнее достигается за счет включения в МЭБС экспертов разной природы и статистической независимости данных в обучающих последовательностей экспертов системы.