Многокаскадный волоконно-оптический усилитель с контролем ширины спектра усиливаемых импульсов

ляется одним из основных проблемных мест си-миляритонной модели, препятствующих достижению высоких энергий импульса [3].

В настоящей работе предлагается каскадная полностью волоконная схема усиления лазерных импульсов, использующая световоды с изменяющейся нормальной ДГС. При помощи подбора профилей ДГС усилителей и пассивных световодов-модуляторов возможно контролировать ширину спектра импульса, поддерживая ее в пределах полосы усиления (максимум ~ 60 нм).

Рассмотрим динамику оптического импульса в световоде с изменяющейся нормальной ДГС Mz ) > 0 и постоянным усилением. Для временной огибающей импульса u ( t, z ) справедливо нелинейное уравнение Шредингера (НУШ)

д u . Р₂(z ) д ² и d z”^z 2 dt^

+ i y \и |²

Г и = —и,

где z – координата вдоль волокна, t – время в сопутствующей с импульсом системе координат, Г — постоянный коэффициент усиления. В настоящей работе мы ограничим рассмотрение случаем распространения импульса в световодах с изменяющейся ДГС и постоянным при этом параметре нелинейности волокна У, что справедливо, например, для световодов с W-профилем показателя преломления в поперечном сечении, изготавливаемых в НЦВО РАН. Технология их вытяжки позволяет достигать существенного изменения ДГС за счет небольшой вариации диаметра волокна, при этом площадь моды и коэффициент нелинейности с большой степенью точности вдоль такого световода можно считать постоянными [4, 5]. Важно также отметить, что в таких световодах удается создавать необходимое по длине распределение ДГС при сверхма- лых значениях дисперсионного параметра третьего порядка, что подтверждает справедливость исходного уравнения (1), записанного в пренебрежении высших порядков дисперсии.

Параметр дисперсии представим в виде 3 ₂( z ) = 3 ₂₀d ( z ) , где под 3 ₂₀ будем понимать значение дисперсии групповых скоростей (ДГС) на входе в световод. Вводя новую переменную

где ф ( ^ ) - фаза импульса, a - постоянная для симиляритона величина чирпа или скорости ЧМ, функция G_par ( t , ^ ) задает форму огибающей параболического импульса и определяется выражением

1    ² / 2^ }. t ^ T s ( ^ )

О ,               t >  ^T s ⁽ ^)

z

£ ( z ) = I d ( z)dz и огибающую импульса j 0

A ( t , z ) = u ( t , z )/ ^d ( z ) , от уравнения (1) мы приходим к уравнению с постоянными дисперсией и нелинейностью, но неоднородным по длине усилением:

dA . 320 a A • I j2 л geУ(^) A i L£_    + 5 A A = ffA , a^ 2 at2     ’ (2)

где эффективный коэффициент усиления может быть записан в виде:

^ge» ^ =           ^1Пd( ^ ^} .     <3)

Можно утверждать, что распространение импульса в световоде с переменной нормальной ДГС 3 2 ( z ) и постоянным усилением p эквивалентно распространению в световоде с постоянной нормальной ДГС и постоянным эффективным усилением при выполнении соотношения

где ф_s ( ^ ) - константа с размерностью времени, определяющая максимальную протяженность импульса по уровню нулевой мощности 2 ф_s . Она связана с длительностью импульса на полувысоте как T FWHM = 2Tt_s . При этом амплитуда и фаза асимптотического параболического решения не зависят от начальной формы импульса, а определяются только начальной энергией импульса E ° и параметрами световода. В случае постоянного усиления g _eff мы можем записать, что при ^ —> ^ справедливы следующие соотношения

geffE0

1/3

^A ® ² ( 75^

^T s ⁽ ^ ) =

exp

g«?

,

a = gfL

3 2 ( £ ) + g 3 ^) = P 3 20 - (4)

Таким образом, задавая профиль изменения ДГС в световоде, возможно влиять на характер его распространения через эффективный коэффициент усиления, физический смысл которого связан с изменением баланса нелинейности и дисперсии. В световодах с убывающей нормальной ДГС относительный рост влияния нелинейности эквивалентен распространению импульса в среде с дополнительным усилением и наоборот, растущий профиль ДГС приводит к относительному уменьшению нелинейности, и распространение импульса происходит в среде с эффективным усилением, сниженным по сравнению с физическим.

Известно, что в активных световодах с нормальной дисперсией возможен самоподобный (симиляритонный) режим распространения импульса, суть которого в том, что огибающая импульса асимптотически при z — ^ стремится к параболической форме, масштабирующейся с ростом координаты импульса [1-3]. Общий вид импульса параболической формы может быть записан как

A ( t , 3 ) = A ( ^ ) G par ( £ t )exp[ i ( ^ ( ^ ) + a t ²)] , (5)

Учитывая выражение для чирпа импульса, уравнение (4) можно переписать в виде:

³ -P 3 , ( z ) + 6 a3 ; (z) = 0 .     (8)

a z

Решением данного уравнения является функция, задающая профиль ДГС, обеспечивающий существование асимптотического решения уравнения (2) в виде ЧМ импульса параболической формы. Это уравнение типа Бернулли. Его решение имеет вид:

₃ , z ) =      P 3 ,0 e ^{p z}

²       P + 6 a3 ₂₀( e ^{p z} - 1)"          ⁽⁹⁾

Данный профиль ДГС обеспечивает постоянное эффективное усиление g _eff = 6 a3 ₂₀ при наличии постоянного физического усиления p . Отметим, что для пассивного световода c пренебрежимо малыми оптическими потерями, т. е. в случае Р — 0 , мы получаем известный результат [6], заключающийся в том, что профиль ДГС пассивного волокна, удовлетворяющий условию существования симиляритона, должен иметь гиперболический вид

³ 2^{( z} ’ = x+a^z ■         (10)

Следует подчеркнуть важный факт, заключа-

ющийся в том, что в пассивном волокне-тэйпере формируется параболический импульс с чирпом a , при этом величиной чирпа можно управлять, выбирая параметры тэйпера – начальное значение ДГС 3 20 и постоянную убывания 6 а3 ₂₀ .

Рассмотрим теперь стандартную схему усиления импульсов в активных световодах с постоянной нормальной ДГС, которая описывается уравнением (1), причем 3 2 (z ) = 3 2 = const . При высоком значении коэффициента усиления Г> 0.1 м ^-1 наблюдается быстрый выход импульса на симиляритонную асимптотику, которая описывается соотношениями (7) с учетом т^ого, что § = z , A ( t , z ) = u ( t , z ) и д ефф = ^Г . Энергия импульса растет экспоненциально по

мощного усиления ДГС световода быстро растет согласно (9), снижая эффективный инкремент усиления и скорость частотной модуляции импульса. Между собой усилительные участки соединяются пассивными световодами с уменьшающейся ДГС, в которых дисперсия гиперболически спадает (согласно (10)) до начального значения, причем постоянная убывания подбирается таким образом, чтобы ограничить скорость частотной модуляции и ширину спектра импульса. Структура каскада показана на рис. 1.

Отметим некоторые особенности. Профиль ДГС начального усилительного элемента каскада задается, исходя из обеспечиваемого физического усиления Г I

длине активного световода, чирп импульса стабилизируется на значении a = Г /6 3 2 . Параметры нормальной ДГС использующихся на практике световодов W-профиля находятся в пределах 3 2 ~ 10^-27 — 5 ^. 10^-26 с²/м [5], таким образом мощное усиление приводит к сильной ЧМ импульса a >  10 24 с^-2. Рассматривая импульсы с начальной длительностью т 0 = 10^-12-10^-11 с, можно убедиться, что асимптотически, ширина спектра симиляритона пропорциональна скорости ЧМ. Это можно видеть, исходя из оценки

3 2 ( z ) =

^Г 3 e ^Г I z

Г . + g_eff ( e^г I z - 1)

Стартовое значение 3 20 выбирается по возможности минимальным, чтобы обеспечить максимальный диапазон изменения ДГС, эффектив-

Аю ~

— + аТ- = ат

2 ^{ss .}

^т 0

ное усиление в первом элементе можно положить g ef = 0 , таким образом 3 2 ( z ) = 3 20 e ^Г I z • При невысокой пиковой мощности начального импульса усиление в первом элементе каскада происходит практически в линейном режиме, так как хотя мощность импульса испытывает экспоненциальный рост, отношение коэффициентов нелинейности и дисперсии так же экспоненци-

Отмечаем, что ширина спектра импульса быстро растет по длине усилителя Аю = ехр( Г z /3) и при мощном усилении быстро выходит за пределы полосы усиления, таким образом, получение симиляритонов высоких энергий ограничено препятствием в виде конечного спектра существующих усилителей. Эрбиевые волоконно-оптические усилители (EDFA) с длиной волны X = 1,56 мкм могут обеспечить однородное усиление в диапазоне около 60 нм, или, соответственно, в полосе частот Аю = 5 - 10¹³ c ^{- 1} . Одним из способов снижения чирпа симиляри-тонов является использование в усилителях волокон с большой дисперсией 3 2 >  5 " 10 ²⁶ с²/м [7-8], что, однако, сталкивается с трудностями в реализации одномодового режима распространения и со сравнительно высоким поглощением в волокнах такого типа.

Мы предлагаем каскадную схему усиления лазерных импульсов, которая использует световоды с изменяющейся нормальной ДГС. Суть данной схемы состоит в том, что на участках

ально снижается. Далее усиленный импульс распространяется во втором элементе – пассивном световоде с уменьшающейся ДГС

3 2I ( z ) =

в11

^{1 +} g eff z .

Стартовое значение ДГС второго элемента 3 2 ^I 0 ^I выбирается максимально возможным и близким к значению на выходе первого элемента. Коэффициент гиперболического убывания одновременно является эффективным инкрементом усиления, под действием которого импульс выходит на симиляритонную асимптотику с постоянным чирпом а = g f /6 3 2 I 0 . Значение эффективного усиления следует выбирать таким образом, чтобы чирп не превосходил некоторого предельного значения и уширение спектра импульса лежало в пределах полосы усиления. Для импульсов с начальной длительностью несколько пикосекунд можно фиксировать а ^ 10 2 ³ С ^- 2 , причем чем длиннее усилительный каскад, тем меньшее значение чирпа следует за-

давать. При этом высокое значение З 1 ₀ позволяет выбирать существенное эффективное усиление g eff ^{— 6} «^З 10 , при котором ДГС спадает до минимальных значений на длине нескольких сотен метров.

В дальнейшем профили ДГС выбираются аналогично за тем исключением, что в усилительных элементах дисперсия растет не экспоненциально как в первом элементе, а согласно (9)

З^ ( z ) —

Г В^N е^Nz N З 20 ^e

Г „ + 6 аЗ 2Д e ^Г " z - 1)’

где Г N - физическое усиление в N -м элементе, 3 N — начальное значение его ДГС (минимальное в усилительных элементах). Импульс при усилении в этих элементах сохраняет чирп а . Профили ДГС соединительных пассивных световодов задаются аналогично (12), при распространении в них импульс так же поддерживает постоянную частотную модуляцию со скоростью а . Следует выделить лишь последний световод-модулятор. Спектр симиляритона, прошедшего все усилительные каскады, ограничивать нет необходимости, наоборот, его следует расширить, сообщив импульсу дополнительный высокий линейный чирп, погасив который параболический симиляритон возможно эффективно сжать и получить высокую пиковую мощность. Таким образом, профиль ДГС финального световода следует задать также согласно (12), но эффективный инкремент усиления можно увеличить для получения высокого линейного чир-па импульса.

Мощный импульс с высокой скоростью ЧМ, получаемый на выходе каскада может быть направлен для погашения чирпа и сжатия на элемент, обладающий аномальной дисперсией и минимальной нелинейностью. Предполагается, что это может быть пара дифракционных решеток

Для проверки теоретических результатов было проведено численное моделирование прохождения начального гауссового импульса вида u0 (t) — VP exP (-12 / 21o2)

длительностью t0 - 2.5 пс и пиковой мощностью P0 — 20 Вт (начальная энергия E0 — 88.5 пДж) и длиной волны X — 1557 нм в четырехкаскадном усилителе-модуляторе построенном по изложенной выше схеме. Профиль ДГС усилительного каскада приведен на рис.2. На первом отрезке длиной L1 — 2.6м происходит усиление с инкрементом ГI —1.5м-1, что соответствует общему усилению около 17 дБ. ДГС при этом экспоненциально возрастает З! (z) — З2о eГ'z с начального значения З20 — 10-27 c2 / м до конеч-

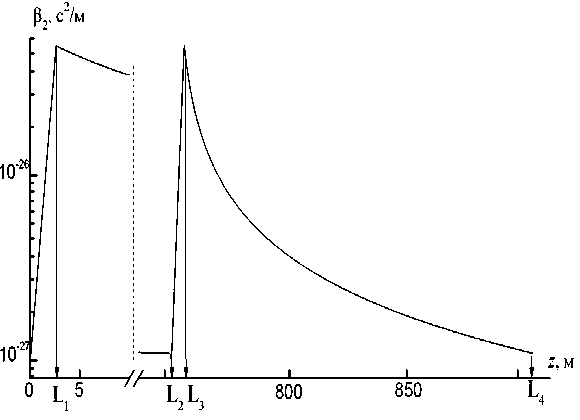
Рис. 2. Профиль ДГС усилительного каскада, использованный для численного моделирования

ного (которое является начальным для второго элемента) З 2 0 — 5 - 10 ^{- 26} c ² / м . Во втором элементе длиной L ₂ — L 1 — 750 м ДГС пассивного световода спадает по закону

З 2 ( z ) —

II

^З 20

1 + 6 • 2 - 10²³ З 2 ₀ ( z - L 1 ) .

Конечное значение ДГС во втором элементе З 2 ( L ₂) — 1.087 • 10 ^{— 27} c ² / м близко к начальному для третьего усилительного элемента З 2 0 I — 10 ^{— 27} c ² / м . Третий элемент длиной L 3 — L ₂ — 5 м обладает инкрементом усиления Г III — 0.8 м ^{— 1} и общим усилением около 17, 4 дБ. Его ДГС растет согласно

III Г 111 ( z - L 2 )

Я III (zA --------- ^{ш З20} --------------

^З 2 ( ) Г III + 6 • 2 •Ю²³ • С ( e^Г “I ⁽ z ^- L 2 ) -

1), (14)

при этом З™ ( L 3 ) близок к З 2 V — 5 •Ю ^{- 26} c ² / м . Наконец, в пассивном световоде длиной

L 4 - L 3 — 150 м ДГС спадает как

З¹! ( z ) —

IV

З ₂₀

1 + 6 •Ю²⁴ З¹ ! ( z - L 3 )

до финального значения З ! ( L ₄) —1.087•Ю ^{- 27} с ²/ м . Моделирование проводилось в предположении, что коэффициент нелинейности постоянен по длине каскада и равен Y = 3.33 Вт"¹км"¹.

На рис. 3 представлены результаты моделирования – эволюция изменения мгновенной частоты и формы огибающей импульса при прохождении каскада. Можно видеть, что в первом элементе импульс усиливается практически сохраняя гауссову форму огибающей и приобретая невысокую ЧМ. На втором этапе импульс, проходя световод с уменьшающейся ДГС (13), выходит на симиляритонную асимптотику, его огибающая приобретает параболическую форму, а изменение мгновенной частоты растет линейно Д ^ — 2 а 1 , где чирп в соответствии с (13)

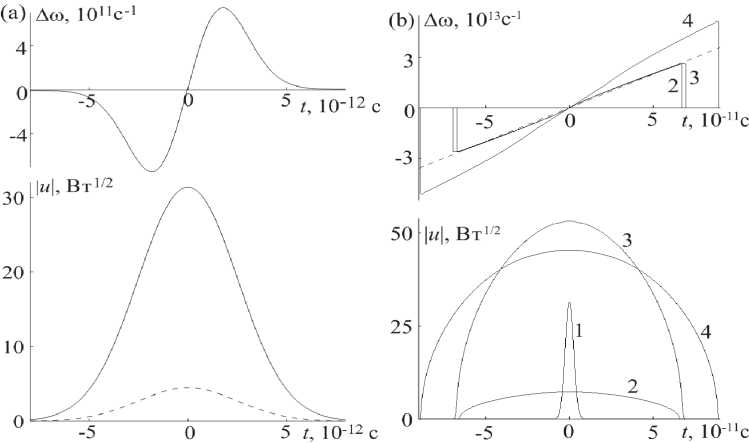
Рис. 3. Результаты численного моделирования:

(a): изменение мгновенной частоты и форма огибающей импульса после прохождения первого элемента каскада. Начальный импульс показан штриховой линией. (b): эволюция изменения мгновенной частоты и формы огибающей импульса при прохождении каскада. 1– после первого элемента, 2– второго, 3–третьего, 4 – на выходе из каскада. Штриховой линией на графике изменения мгновенной частоты показана асимптотика A to = 2 a t , a = 2 ■ 10²³ c ^{- 2}

a = 2 ■ IO²³ c ² . Далее можно видеть, что в третьем усилительном элементе чирп импульса сохраняется, и увеличение мощности происходит практически без роста ЧМ. Наконец, на выходе из каскада импульс приобретает повышенный чирп, отмечаем, что он отклоняется от линейной зависимости, что можно объяснить неполным сближением с асимптотическим решением.

На рис. 4 показана эволюция спектра импульса. Отмечаем, что на участках усиления с

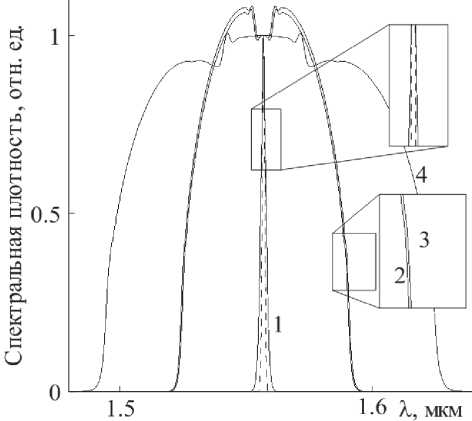
Рис. 4. Результаты численного моделирования. Эволюция спектра импульса при прохождении усилительного каскада: 1 – после первого элемента; 2 – после второго; 3 – после третьего; 4 – на выходе из каскада. Штриховой линией обозначен спектр начального импульса

быстрорастущей ДГС спектр импульса изменяется незначительно. Уширение спектра происходит в пассивных световодах-модуляторах с уменьшающейся ДГС. Скорость частотной модуляции в световоде, соединяющем усилители, задана таким образом, чтобы ширина спектра импульса не превосходила ширины спектра усиления ~ 60 нм. В последнем элементе каскада спектр резко уширяется, вследствие повышения скорости ЧМ. В итоге, на выходе каскада получен импульс с формой огибающей близкой к параболической, его длительность T fwhm ~ 1.2 10^-10 с, пиковая мощность P = 2.8 кВт, энергия E = 317 нДж = 3.58x10 3 E 0 . Проведено моделирование компрессии полученного импульса на линейном диспергирующем элементе с аномальной дисперсией ^ 2 ■A L = - 1.545 ■ IO ²⁴ с ² . Результаты представлены на рис. 5. Полученный в результате импульс обладает пиковой мощностью немного менее 800 кВт. Отмечаем правильную форму сжатого импульса с наличием дифракционных максимумов первых порядков.

Для сравнения было проведено моделирование прохождения импульса в усилителе с постоянной ДГС, равной среднему значению ДГС в каскаде при сохранении величины общего усиления. Усреднение ДГС проведено по трем первым элементам каскада, в которых ширина спектра импульса ограничивалась. Получено среднее значение ДГС

L ₁

L                      2

А = _Г И ft. ( - ) dz * f ft ! ( z ) dz *

L

L

L ₁

-7 5 1И12’ Ю5 Вт

5"

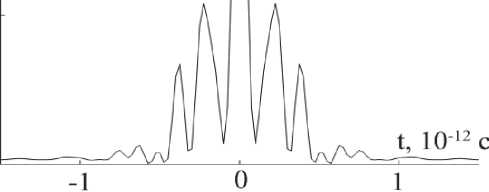
Рис. 5. Результат компрессии импульса, полученного на выходе усилительного каскада

L 3

+ j P™ ( z ) dz >

L 2                   ^

= 4.3 - 10 27 c / м - ² .

Длина усилителя с постоянной ДГС выбрана равной длине трехэлементного каскада L3 . При этом при условии равного общего усиления получаем, что инкремент усиления в нем равен Г = 0.0104 м-1. Результаты сравнения представлены на рис.6. Как можно видеть, ширина спектра импульса, прошедшего усилитель с постоянной ДГС значительно шире чем у импульса, прошедшего каскад. Это можно объяснить повышенным значением чирпа у импульса, усиленного при постоянной ДГС. Действительно, при усилении импульс выходитна симиляритон-ную асимптотику со скоростью ЧМ a = Г / 6Р2 = 4.03 -1023 с-2 > a , что и приводит к значительной ширине спектра AXFWHM = 150 нм. Таким образом, реальное получение мощных импульсов в усилителях с постоянной ДГС крайне затруднительно, вследствие недостаточной ширины полосы усиления. Альтернативным способом может стать предложенная каскадная схема усиления с использованием световодов с изменяющейся ДГС.

В заключение сформулируем выводы: в работе предложена каскадная полностью волоконная схема усиления лазерных импульсов, использующая световоды с изменяющейся нормальной ДГС. Усиление предполагается производить на участках с быстрым, близким к экспоненциальному, ростом нормальной дисперсии. Участки усиления соединяются пассивными световодами с уменьшающейся нормальной ДГС. В процессе распространения в каскаде импульс трансформируется в параболический си-миляритон, скоростью частотной модуляции которого возможно управлять при помощи подбора профилей дисперсии усилителей и пассивных световодов-модуляторов. Отметим, что скорость частотной модуляции можно снижать, выбирая пассивные световоды большой длины с меньшей скоростью снижения ДГС, при этом число усилительных элементов можно увеличить. Использование данной схемы позволяет контролировать ширину спектра импульса, поддерживая ее в пределах полосы усиления (максимум ~ 60 нм) и получать симиляритонные им-

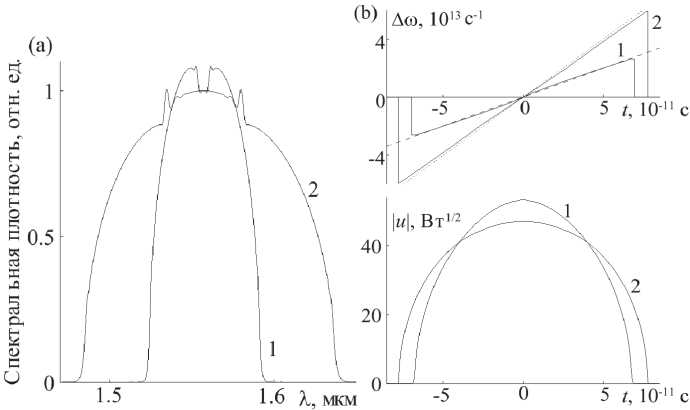
Рис. 6. Сравнение характеристик импульсов прошедших

1 – три каскада усилительной схемы, 2 – усилитель с постоянной ДГС и постоянным усилением. Длина и средние значения усиления и ДГС в обоих случаях равны. (а) – спектры импульсов, (b) – изменения мгновенной частоты и формы огибающих. Прямыми на графике изменения мгновенной частоты показаны асимптотики: штриховая - A to = 2 at, a = 2 - 1 0 ²³ c^² , пунктирная - A to = 2 at , a = 4.03 -10²³ c "²

пульсы сверхвысоких энергий – до 1 мкДж и выше.При помощи финального модулятора мощному выходному импульсу возможно сообщить высокий линейный чирп, что позволит его эффективно сжать и достичь рекордных пиковых мощностей более 1 МВт.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках федеральных целевых программ «Научные и научно-педагогические кадры инновационной России на 2009 - 2013 годы» и «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы».