Многокомпонентные оптоэлектронные структуры спектрального взаимодействия в качестве адаптивных элементов оптики

Воздействие информационных параметров в оптоэлектронных устройствах (ОЭУ) происходит, в основном, двумя способами: 1 - путем пространственно-временной модуляции светового потока некогерентного излучения (к этому же, в конечном счете, сводится и изменение степени и направления поляризации излучения); 2 - путем интерференционного взаимодействия когерентных компонент излучения и их модуляции, т.е. путем воздействия на амплитуду (интенсивность) и фазу световой волны.

В тоже время, использование принципа спектрального взаимодействия оптических элементов позволяет получить достаточно эффективные и простые по конструктивному исполнению ОЭУ. В многокомпонентных оптронных структурах (МОС) спектрального взаимодействия (рис. 1) на поверхность оптоэлектронных элементов (ОЭЭ), т.е. на поверхность источника излучение (ИИ), элементов оптической системы (ОС) и приемника излучения (ПИ), наносится дополнительный ряд компонент (2, 3, 5, 6), выполняемых в виде многослойных тонкопленочных покрытий (МТП). Эти компоненты, выполняя спектроформирующую функцию, функцию избирательной, временной и пространственной фильтрации, модуляции и коммутации, существенно изменяют свойства ОЭЭ. Здесь воздействие информационных параметров происходит в результате спектрального взаимодействия многокомпонентных оптоэлектронных элементов - в результате взаимного движения их спектральных характеристик. Такое движение спектральных характеристик может быть осуществлено различными путями: воздействием тепловых, электрических, магнитных, акустических полей, изменением

Рис. 1. структурная схема МОС

В результате такого взаимодействия становится возможным добиться инвариантности параметров ОЭУ к внешним дестабилизирующим факторам -температуре окружающей среды, вибрации и т.д., реализовать функцию временной и пространствен- ной модуляции, коммутации, спектрального уплотнения и создать прецизионные ОЭЭ и ОЭУ систем управления, измерения и контроля [1].

Многокомпонентные оптоэлектронные элементы спектрального взаимодействия - это оптоэлектронные элементы, в оптическую цепь которых введены (на поверхность которых нанесены) компоненты, выполняющие спектроформирующую и спектровзаимодействующую функции, функции пространственной и временной фильтрации и модуляции.

Многокомпонентные оптоэлектронные системы спектрального взаимодействия (МОС) - это оптоэлектронные устройства, содержащие хотя бы один многокомпонентный оптоэлектронный элемент, воздействие информативных параметров в которых происходит в следствии взаимодействия спектральных характеристик.

Математическая модель МОС

Если обозначить Ф (Я,т и _Ф ) , Т (Я, t т, и _т ) , £(Л t , t ,U _s ) - абсолютные спектральные характеристики излучения ИИ, пропускания ОС и чувствительности ПИ, и_ф , U_T,U_S - управляющие сигналы ИИ, ОС и ПИ, а Ф‘ ( Я , t,т), Т * ( Я , t,т), S k ( Я , t ,t) - абсолютные спектральные характеристики пропускания i, J, k-го МТП, нанесенных на поверхности ИИ, ОС и ПИ соответственно, то для последовательно соединенных МОЭ спектральный состав излучения I * (Я, t , т ), падающего на фоточув-ствительную площадку ПИ, определится из выражения:

I * (Я, t, т) = {Ф *(Я, t ,т, иф) -П ФП (Я, t ,т)} ■ i∈I

{ T * ( Я , t ,т, U t ) -П Т * ( Я , t ,т )} ■ { S * ( Я , t ,т, U s ) ■ , j ∈ J

П snk (Я, t ,т)} k∈K где I, J, K - множество индексов компонент МТП, нанесенных на ИИ, элементы ОС и ПИ соответственно.

В большинстве случаев [1] с достаточной степенью точности и не зависимо от физической природы процессов, происходящих в оптоэлектронных элементах, их абсолютные спектральные характеристики можно аппроксимировать разностными функциями вида:

Ф * ( Я , t , т , и ф ) = Ф м ( t , т , и ф ) ■ Ф [ Я - Я ф ( t , т )],

T * ( Я , t , т , U_T ) = Т м ( t , т , U_T ) ■ Т [ Я - Я ( t ,т )],     (1)

S* (Я, t, т, Us ) = Sm (t, т, Us ) ■ S[Я - Яs (t)], где: ФА-X* (t ,т)], Т [ X - Хт (t, т)], 5 [X - Xs (t ,т)] - относительные спектральные характеристики мощности излучения ИИ, пропускания ОС и чувствительности ПИ соответственно; Фм (t, т, И ф), Т. (t, т, И Т), 5м (t, т, И 5) - температурно-временные зависимости изменения максимумов их абсолютных спектральных характеристик; Хф(t,т), XT(t,т), Xs(t,т)- температурно-временные зависимости длин волн максимумов соответствующих спектральных характеристик.

С учетом (1) спектральные характеристики элементов МОС определятся:

Ф * ( X , t , т , И ф , И Ф , U X ) = Ф . ( t , т , И ф ) ■ Ф [ X - X ф ( t , т )] ■ П Ф . п ( t , т , и Пф ) ■ Ф П [ X - X ф п ( t , т , И ^ ф )];

Т * ( X , t , т , И т , И „, , U X ) = Т м ( t , т , И т ) ■ т [ X - X t ( t , т )] ■ П Т мп ( t , т , Ик ) ■ Пи - X Tn ( t , т , u x )];

5’(X, t, И5, И k, И„kx5) = 5м (t, т, И5) ■ 5[X - Xs (t)] ■ П 5Мп (t, т, Ик) ■ 5k [X - Xk (t, т, Ик5 )], k∈K где И„ф, И„т, Ик - управляющие воздействия на максимумы пропускания соответствующих МТП, ИФ, UXT, Us - управляющие воздействия на сдвиг спектральных характеристик МТП.

Так как в общем случае для МОС наблюдается координатная зависимость их спектральных характеристик (по поверхности элементов), то их абсолютные спектральные характеристики (обозначены знаком « ** ») запишутся в виде:

Ф “ ( x , y , z , X , t ,т, Ик) = Ф * ( X , t , т , И ф , И „ф , U X ) ■ ^GФ ⁽ x , y , ^z );

т “ ( x , y , z , X , t , т , И Т ) = Т * ( X , t , т , И т , И „т , U X ) ■ G t ( x , У , z );

5 ” (x, y, z, X, t ,т, И^) = 5 * (X, t, И5, Ик, Ик5) ■ G5 (x, y,z ), где: Оф(x,y,z), Gt(x,y,z), Gs (x, y, z)- весовые функции, учитывающие координатную зависимость соответствующих спектральных характеристик ИИ, ОС, ПИ соответственно, а Иф*,ИТ*,И5‘ - множество управляющих воздействий МОЭ. Тогда с учетом выражения для освещенности [2] чувствительной площадки РП ПИ от смещенного относительно него на величину x0, y0 ИИ с излучающей площадкой РИ, получим обобщенное выражение для величины выходного сигнала ПИ в виде:

ijki jk

J ( t , ^т , ^U ф , ^U т , ^U 5 , ^U пФ , ^U nT , ^U п5 , ^U nXФ , ^U nXT , ^U nX5 )

λ _В

= J <Л 4- Jf z

^X H ^Р П ^{0 Р} И

Ф "( x 0 , y 0 , z 0 , X , t , т , И_ф) ■ Т " ( x , y , z , X , t , т , И Т ) ^[( ^{x - x} 0 )^{2 +} ( y ^- y 0 )^{2 + z} 0 ^2]

x 5 ** ( x , y , z , X , t , т , И 5 *) ■ dx ₀ dy ₀ dx dy } d X .

Выражение (2) позволяет учесть как влияние информационных и управляющих воздействий на элементы МОС, так и влияние внешних дестабилизирующих факторов (ВДФ).

В таб. 1 с позиций теории чувствительности приведены выражения для определения чувствительность МОС a I = A J / J к изменению управляющих сигналов и ВДФ.

В таблице приняты следующие условные обозначения:

1      д Ф м ( t , т , И ф )

--, ^Ф м ⁽ t ^{, т} , ^И Ф )      ^дт

τ

^α SМ ⁼

1      e s_ ( t , т , и₅ )

мS

--,

5м (t ,т, И5 )     дт a =    1 дТ. (t,т, Ит)

^М Т . (t , т , И т ) д т

ОС, ПИ;

-

инерционность ИИ,

iτ α ФМn ⁼

1       д Ф „ ( t, т , И ф )

—■— --------,

Фп (t,т, ИФ )     дт ajт =     1     дТ.„ (t ,т, Ит)

0MM"  Tj (t ,т, Ит)     дт     ’ ат =     1     85к (t ,т, Ит)

^5Mn  5к ( t , т , И т )      д т

-

инерционность ИИ,

ОС, ПИ по цепи управления МТП;

_a = 1 8 Ф . ( t , т , И ф ) ФМ ф . (t, т ,И ф ) a t ’

. =      ^{1      д Т} м ⁽ t ^{, т} , ^И Т )

" М” т . (t, т ,И т )      a t

,

1      d S . (t , т , Ц )

5. (t ,т, U5)     at тельность ИИ, ОС, ПИ;

-

температурная чувстви-

, t =       1       Э Ф ., ( t, т , И ф )

^М Ф.(t,т,Иф)     а^     ’ оХ =    дТ^,

"™ т..(t, т ,И т )      a t

O k =____ ¹____ ^д' ⁵ 'п ⁽ t ^{, т} , ^{И т} ) - температурная чувст-

5М 5. (t,т, Ит)     at вительность ИИ, ОС, ПИ по цепи МТП;

_о = 1 d X _? ( t , r )

X® X»(t,т) дт ’ тт _   1   8X(t,т)

,

/X (t ,т) дт аУ = —1— dX; (t,т) - инерционность изменения X; (t ,т) дт длин волн максимумов спектральных характеристик ИИ, ОС, ПИ;

A * = Ф [ X - Xф ( t , т )] ■ || Ф¹,, [ X - Xф „ ( t , т , U X )] ■ Т [ X - X t ( t , т )] ■

П Т п [ X - XT„ ( t , т , И-„ X T )] ■ 5 [ X - Xs ( t )] ■ П 5 п [ X - Xk ( t , т , U^k „ X _S )] d X i ∈ J                                                  k ∈ K

λ _В

A = J A 1 d X λ _Н

. лт =       1      d X kn (t,т,И„ X Ф )

’ "Ф1 Xin(t,т,ЦФ)     дт     ’ т =      1      дД(t,T,U),

T T ( t ^т U T )     ^{д т}

TT =      1      дД ( t , T , U )

S’ s (t ,т, Uns)      дт инерционность

изменения длин волн максимумов спектральных характеристик МТП соответственно ИИ, ОС, ПИ;

_а = 1 дД » (t , т )    , = 1 C s (t , т ) _а = 1 д Д (t , т ) -

» т»(t,т) Ct ’ ” ST(t,т) Ct ’ ж s(t,т) Ct температурные коэффициенты изменения длин волн максимумов спектральных характеристик ИИ, ОС, ПИ;

_а  =        1        is , ( t ,т, 1. » )

»’ ф( (t ,т, Uns»)      dt      , а =     1    cs, (t т UnT)

" < (t ,т, Ut)     dt     ’ o" =-----1----dTsn (t,т, US)   - температурные

S (t ,т, US)     at коэффициенты изменения длин волн максимумов спектральных характеристик МТП соответственно ИИ, ОС, ПИ;

в -д»^, в -CTTM, в s - крутиз-λФ                  λT

∂λФ             ∂λT на спектральной характеристики ИИ, ОС, ПИ;

_ d»[s-S » ]         _ ату,- л , ]       _ a s k [ s -4]

P»      --i ’    PsTn      -.1     ’    Pss-

∂λФn                  ∂λTn                 ∂λSn крутизна спектральной характеристики МТП соответственно ИИ, ОС, ПИ;

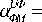
1      дФ м ( t ,т, U » )

»m (t ,т, U»)

1      CT . (t т U t )

Tm (t ,т, Ut )

1       CS. ( t ,т, U s )

Sm (t т Us)

чувствительность

максимумов спектральных характеристик ИИ, ОС, ПИ к соответствующим управляющим воздействиям;

_av» =     1     дФ м, (t т и )

»М ». (t ,т, Un)

, UT =       1     ar ( t ,т, U n )

T^MM T (t т U ) dU^j ’ Mn ⁽ t ,^т, U Tn )      U TTn

O US  ----¹---- ^{a S Mh (t , т} ’ U S’ ) - чувствительность

М* Sm (t ,т, US’)    eUkn максимумов спектральных характеристик МТП соответственно ИИ, ОС, ПИ к соответствующим управляющим воздействиям;

_{a m} =      1      дД фп ( t ,т, U s » )

”" Дф (t,т,UnT»)    CUnT»    ’ aU =     1     asTn (t ,т, U’TT)

STn j„ (t ,т, U’TT)    CUtt    ’ aUS ------1----aTsn(t,т’US) - чувствительность

S”* ts(t,т,Uss)    aUnss изменения длин волн максимумов спектральных характеристик МТП соответственно ИИ, ОС, ПИ к соответствующим управляющим воздействиям.

Как видно из (2) и таблицы 1 выходной сигнал ПИ определяется величиной излучаемого ИИ светового потока, спектральными характеристиками МОЭ и взаимодействием этих спектральных характеристик. Причем, этим взаимодействием можно управлять как путем изменения соответствующих управляющих воздействий, так и изменением крутизны и взаимного расположения спектральных характеристик элементов.

Таблица 1.

Чувствительность МОС к управляющим воздействиям и ВДФ

Воздействие	Коэффициент чувствительности
время А т	τ       τ       τ            τ             j τ            k τ α ФМ + α SМ + α TМ + ∑ α ФМn + ∑ α TMn + ∑ α SMn + jk 4 j A '[T.» P » a » + S s P s s a l s ^ + Т^ Р а гХт + A λ Н S T »„ P k « i»„ + s T Tj„ P T r„ a ; j ; „ + E Sn ea ds. ] d S i ∈ I                       j ∈ J                     k ∈ K
температура А t	t              t             t                     it                       jt                    kt α ФМ + α SМ + α TМ + ∑ α ФМn + ∑ α TММ + ∑ α SММ + i                j               k 1) A •[ » P » » O, » + ”S P ,A + TP т ак т + A Н S S »„ P i»„ « i'»„ + S Т Т„ Р Д г „ а Т„ + S Т кт„ в к„ а к”„ ] d S i ∈ I                       j ∈ J                    k ∈ K
интенсивность излучения ИИ A U » , A U ’»	UФ               iUФ     i а »М A U » + S a »Mn A U n» i
пропускание ОС AU t , AU nT	а ТМ A U t + £ «S , A U nT
чувствительность ПИ A Us ’ A U S	US               kUS     k « SM A U S + S « SMn A U nS k
Сдвиг спектральной характеристики МТП ИИ A U ’ s »	— J A 1 [ S S »„ P i»„ a i»n A U n» ] d S A Н     i ∈ I
Сдвиг спектральной характеристики МТП ОС A U ’ t t	— J A 1 [ S S Tn P S t, « U A U T t ] d S A Н j ∈ J
Сдвиг спектральной характеристики МТП A U S	1 — [A i [У т ф р к,„ « SU S a US ] d s 1             S’ Anfl Anfl       nSa A Н    k ∈ K

Многокомпонентные адаптивные элементы оптики

Оптика когерентного излучения и, особенно, компьютерная оптика, являясь частью современных вычислительных оптических систем, нашла широкое применение благодаря способности к адаптации, гибкости в перенастройке, высокой скорости обработки информации. Применение когерентной оптики предполагает использование достаточно сложных и громоздких оптических систем. В тоже время, многие вычислительные задачи можно решить, используя элементы некогерентной оптики: модуляторы и демодуляторы, корректоры нелинейности, дефлекторы, коммутаторы оптического сигнала и др. На рис. 2 изображена конструкция простейшего адаптивного оптического фильтра.

оптического излучения

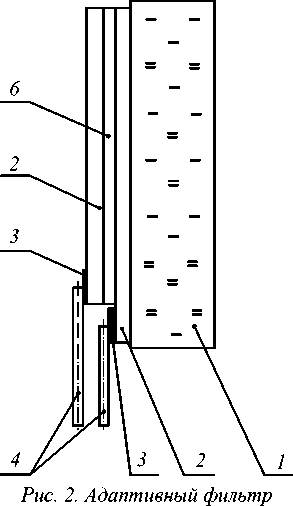
Он состоит из стеклянной подложки 1, на которую между двумя прозрачными омическими электродами 2 нанесены тонкопленочные слои интерференционного фильтра 6. К омическим электродам 2 подводится управляющее напряжение с помощью выводов 4. Резонансный слой такого спектроформирующего элемента (СФЭ) выполнятся из материала, обладающего электрооптическим, электрострикционным или обратным пьезоэффектом. При изменении управляющего напряжения изменяется показатель преломления резонансного слоя фильтра или его толщина и, в соответствии с выражениями таб. 1, изменяется длина волны максимума пропускания (рис. 3). Зависимость величины показателя преломления и толщины резонансного слоя СФЭ от управляющего напряжения для некоторых материалов линейная, для других - близка к квадратичной, зависимость же длины волны максимума пропускания адаптивного СФЭ от управляющего напряжения близка к косинусоидальной.

Ясно, что из-за небольших величин электро- и пьезооптических постоянных материалов СФЭ диапазон изменения максимума пропускания СФЭ небольшой. Однако, используя метод спектрального взаимодействия элементов, можно существенно улучшить характеристики.

Так, если на обратную сторону стеклянной подложки адаптивного фильтра (см. рис. 2) нанести такую же многослойную спектроформирующую систему, то возможна реализация функции модулятора оптического излучения, управляемого с помощью одного или двух напряжений. Если величины управляющих на- пряжений выбрать так, чтобы спектральные характеристики при их изменении не перекрывались между собой или перекрывались частично (рис. 3), то такой оптический элемент реализует функцию электрооптического затвора с функцией «И» по управляющим напряжениям или функцию регулируемого ослабителя оптического излучения соответственно.

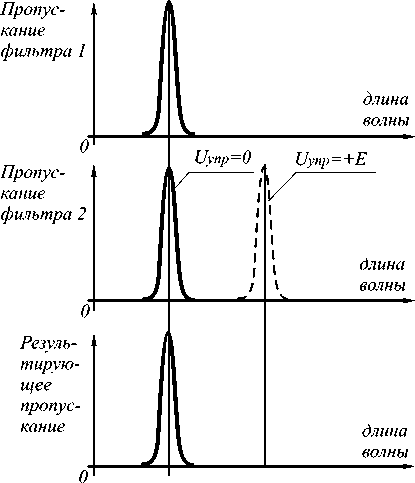
Рис. 3. Спектральные характеристики пропускания адаптивного фильтра при различных управляющих напряжениях

Выходной сигнал ПИ такого элемента определится из выражения:

λВ

J ( U n ¹ λ T , U n ² λ T ) = a ∫ Ф ( λ ) ⋅ S ( λ ) ⋅ Т ¹ п [ λ , U ¹ n λ Т , U ¹ d λ Т ] ⋅ ^λ Н

⋅ Т п ² [ λ , U n ² λ Т U d ² λ Т ] ⋅ dλ ,

Т пⁱ [ λ , U nⁱ λ Т , U dⁱ λ Т ] =

π n 2 d 2 (1 + α n^U U nⁱ λ Т )(1 + α d^U U dⁱ λ Т )

H + D cos[

λ

]

где i=1, 2, α_n ^U , α_d ^U - электрооптический коэффициент и коэффициент линейного расширения материала СФЭ вследствие электрострикционного или обратного пьезоэффекта соответственно.

На рис. 4 изображена зависимость пропускания такого модулятора оптического излучения от величины управляющего напряжения (параметр D определяет полосу пропускания СФЭ), а на рис. 5 -зависимость величины управляющего напряжения от полосы пропускания СФЭ.

Диапазон изменения управляющих напряжений ∆ U (измеренный по уровню 0,2) определяется соотношением величин электрооптического (элек-трострикционного, пьезо-) коэффициента и полосой пропускания СФЭ:

∆ U

1 α n ^U

2 π N - arcCos (8/ D - 1) _-1

2 π N + arcCos (8/ D - 1)

Рис. 4. Характеристика пропускания модулятора оптического излучения

U 2 < X ) = U упр 2 X / X m — U упр 3 , где X_m - размер дефлектора в направлении координаты X .

К электродам 1, 3 фильтра 2 подключен источник управляющего напряжения U_yпр1 . Учитывая координатные зависимости оптических толщин n d_ резонансных слоев СФЭ 2 и 6:

n2 d2 ( x) = n20 d20 (1 + aUUупр 1 ) , n 6( X ) = n 60 d 6o{1+a (Uупр 2

x

^U упр 3^)} , x_m

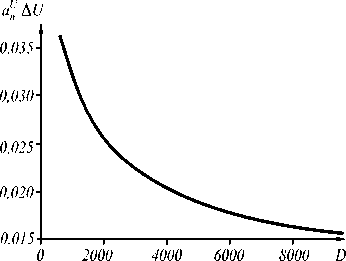
Рис. 5. Связь диапазона управляющих напряжений и электрооптических свойств материалов

На рис. 6 изображена конструкция оптического дефлектора, реализованного на методе спектрально-

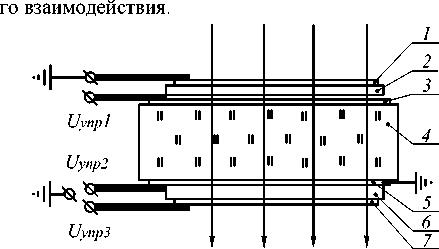
Рис. 6. Аналоговый тонкопленочный дефлектор некогерентного оптического излучения.

Он состоит из двух идентичных узкополосных тонкопленочных интерференционных фильтров, выполненных из нанесенных на подложку 4 оптически прозрачных электродов 1, 3, 5, 7 (окись олова), резонансных полуволновых и зеркальных слоев 2, 6 из материалов, обладающих электрооптическим, электрострикционным или обратным пьезоэффектом (сернистый цинк, криолит и др.). К электроду 5 фильтра 6 с двух сторон с помощью низкоомных электродов подключен источник развертывающего напряжения U_yпр2 , создающий линейное падение напряжения в электроде 5. Ко второму электроду 7 фильтра 6 подключен источник управляющего напряжения U_yпр3 . В результате между электродами 5, 6 фильтра 6 создается линейно изменяющаяся разность потенциалов U₂(X) :

где n ₂₀, n ₆₀, d ₂₀, d ₆₀ - показатели преломления и толщины резонансных слоев СФЭ 2 и 6 при отсутствии управляющих напряжений, определим координату Х наибольшего пропускания дефлектора:

X =

U+U упр1     упр3 v _ v

— X m = ^Y ■ X m .

^U упр 2

Как видно, координатная зависимость максимума пропускания дефлектора линейная, определяется только величинами управляющих напряжений и не зависит от свойств и стабильности материалов СФЭ. Ширину области прозрачности дефлектора A X (по уровню 0,5) можно определить из соотношения электрооптического коэффициента материала СФЭ, управляющих напряжений и полос пропускания спектроформирующих элементов (рис. 7):

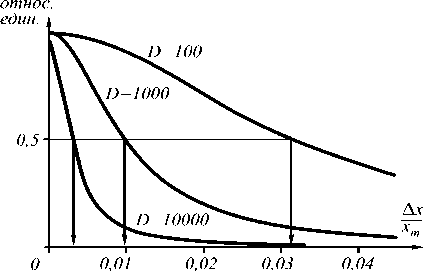
Рис. 7. Зависимость ширины области прозрачности дефлектора от полосы пропускания СФЭ

λ _В ∫ λ Н

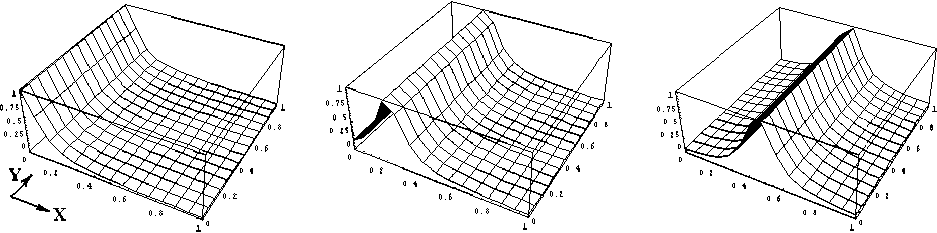
γ=0                        γ=0,25                        γ=0,5

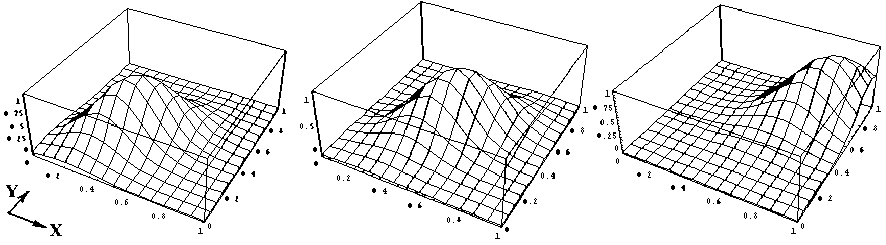
Рис.8. Пропускание дефлектора при различных управляющих напряжениях y = (и ,+ и а/и ..

< m        упр 1       упр 3        упр 2

γ=0                       γ=0,25                          γ=0,5

Рис. 9. Пропускание двухкоординатного дефлектора при различных управляющих напряжениях

у = (U _l+ U a²/ U U , / m        упр 1       упр 3         упр 2 упр 4

При введении в конструкцию дефлектора третьего фильтра (см. рис. 6), идентичного фильтру 6, но пространственно развернутого на 90⁰ вдоль оси Z , и подаче на его электроды соответствующего управляющего напряжения и_упр4 , устройство реализует функцию двухкоординатного сканирования (рис. 9).

Ширину области прозрачности дефлектора NX , A Y (по уровню 0,5) можно определить из соотношения электрооптического коэффициента материала СФЭ, управляющих напряжений и полос пропускания спектроформирующих элементов:

пропускания дефлектора ограничивается как соотношением полосы пропускания СФЭ и величины электрооптического коэффициента, так и шириной электродов (полос), а, поэтому, может быть уже, чем в варианте рис. 6.

λВ

∫ л (H + D cos[B(1 + a" {Uупр2

т . ‘( л и упр , ) • Ф W-S ( Л ) • d A

^A X + " упр , $)/ Л ])( H + D cos[ B (1 + a " { U „ 4

Xm

ДУ „

V + ^U упр- V)'^л ]) y_m

λВ

= 0,5 J T . '( Л , " упр J³ Ф ( Л ) . S ( Л ) . d A ;

λ Н

T* . ( л , U уп^ ) =

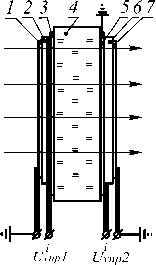
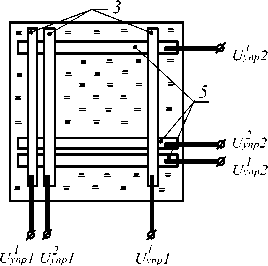
Рис. 10. Дискретный тонкопленочный дефлектор (коммутатор) некогерентного оптического излучения

H + D cos[ B (1 + a . U „р; )/ Л ]

где Y m - размер дефлектора в направлении координаты Y .

Вариант реализации дискретного дефлектора, который так же может выполнять функцию многоканального коммутатора некогерентного излучения, изображен на рис. 10. Здесь омические электроды спектроформирующих элементов выполнены в виде системы ортогональных полос, подключенных к независимым источникам управляющего напряжения. Область прозрачности такого дефлектора (коммутатора) находится под перекрестием электродов с одинаковыми управляющими напряжениями. В этой конструкции дефлектора ширина пространственного