Многокомпонентный количественный ПЦР-анализ

В статье [1] были рассмотрены методические особенности и предложен способ моделирования двухкомпонентного сигнала ПЦР. Выполнено сравнение трех способов определения порогового цикла при двухкомпонентных ПЦР-анализах. Определены зависимости погрешностей измерения от разности пороговых циклов измерительного и соседнего спектральных каналов. Показано, что при действии помехи в виде 10 %-х сигналов соседнего канала погрешность пороговых циклов измерительного канала может достигать значения ± 0.3 единицы температурного цикла.

Однако известно, что значительное уменьшение погрешностей может быть получено путем применения алгоритма, который позволяет рассчитать вклад каждого соседнего красителя в измеряемый спектральный сигнал [2]. Один из вариантов такого алгоритма реализован в программном обеспечении анализатора нуклеиновых кислот АНК-32, который серийно выпускается в ИАП РАН [3]. Для компенсации прохождения сигналов каждого из четырех красителей в измеряемые каналы используется матрица пересчета. Если экспериментально подобрать калибровочные коэффициенты, то при дальнейшей работе взаимное влияние красителей соседних каналов будет минимально.

В данной статье предложен способ на основе сигмоидальной (S-образной) функции (СФ), обеспечивающий автоматическую полную компенсацию взаимного влияния красителей соседних спектральных каналов без предварительной калибровки.

ПОСТРОЕНИЕ МНОГОКОМПОНЕНТНЫХ МОДЕЛЬНЫХ СИГНАЛОВ

Для построения модельных сигналов СФ в нескольких каналах использованы аналитическая форма и методика расчета, приведенные в наших статьях [1, 4, 5]:

F = F m / (1 + exp (( C 0 – C ) / k )) +

+ f 0 + f 1 ∙ C + f 2 ∙ C ², (1)

где F — интенсивность флуоресценции, измеряемая в относительных единицах флуоресценции (о. е.); F m — максимальное изменение интенсивности флуоресценции в конце реакции; C — порядковый номер цикла амплификации (от 1 до 50); C ₀ — дробный номер цикла, при котором интенсивность флуоресценции достигает половины значения F m ; k — коэффициент, который определяется наклоном кривой; f 0 — смещение нулевой линии (фон детектора); f 1 — коэффициент, который определяется линейным дрейфом нулевой линии; f 2 — коэффициент, учитывающий квадратичную составляющую дрейфа нулевой линии.

В статье [4] было показано, что дробный цикл C ₀ можно принять в качестве величины порогового цикла C t реального сигнала ПЦР. Ниже приведен пример вычислений трехкомпонентных модельных сигналов СФ с помощью электронной таблицы Excel (таблица).

Компенсационные коэффициенты m и n , а также суммы квадратов сигналов ошибок S k определяются путем дальнейших расчетов. Параметры исходных однокомпонентных моделей были выбраны, исходя из следующих критериев.

Величины C 0 , равные 18.5, 23.5 и 28.5 ед. циклов амплификации, выбраны с разностью, равной 5 циклам, поскольку в статье [1] было показано, что при такой разности наблюдаются максимальные погрешности измерений. Величины F m и f₀ , равные 1000 и 0 о. е., соответствуют обычному динамическому диапазону ПЦР-сигналов после нормализации. Величина к = 1.39 соответствует наклону реальных графиков ПЦР-сигналов.

Вычисления модельных сигналов СФ в 3 каналах выполнялись в следующей последовательности.

Электронная таблица для вычислений трехкомпонентных модельных сигналов СФ

Номер ячейки	Номер цикла С	A	B	C	D	E	N	S
2		m =	-	-	-	0.048	0.097	0.028
3	-	n =	-	-	-	0.056	0.069	0.037
4	-	C 0 =	18.5	23.5	28.5	18.5000	23.4999	28.5000
5	-	F m =	1000	1000	1000	992.9	992.7	995.6
6	-	k =	1.39	1.39	1.39	1.390	1.389	1.390
7	-	f 0 =	0	0	0	0.00	0.01	0.00
8	-	f 1 =	0	0	0	0.00	0.00	0.00
9	-	f 2 =	0	0	0	0.00	0.00	0.00
10	-	S k =	—	—	—	0.00001	0.007	0.0003
11…60	1…50	F 1 …F 50

• 1.    В ячейках В11:В60 вычислялась интенсивность флуоресценции F исходной однокомпонентной модели СФ по формуле (1) с параметрами, приведенными в ячейках В4:В9 , как зависимость от номера цикла C (рисунок, ряд 1).

• 2.    Аналогично в ячейках C11:C60 и D11:D60 вычислялись однокомпонентные модели СФ с параметрами в ячейках C4:С9 и D4:D7 (рисунок, ряд 2 и 3).

• 3.    В следующих ячейках G11:G60 , H11:H60 и I11:I60 (в таблице не показаны) были вычислены трехкомпонентные модели СФ с произвольно выбранными в качестве примера коэффициентами взаимного влияния соседних спектральных каналов от 0.03 до 0.1. В первых ячейках сигналы этих моделей можно выразить следующим образом:

G11=B11+C11*0.05+D11*0.06 , (2)

H11=C11+B11*0.1+D11*0.075 , (3)

I11=D11 + B11*0.04+C11*0.03 . (4)

В этом примере для модельного сигнала G11 в формуле (2) модельные сигналы C11*0.05 и D11*0.06 являются аналогами 5 % и 6 % помех от соседних спектральных каналов. Точно также для модельного сигнала H11 в формуле (3) модельные сигналы B11*0.1 и D11*0.075 являются аналогами 10 % и 7.5 % помех от соседних спектральных каналов.

На рисунке приведены графики модельных сигналов. Видно, что сигнал трехкомпонентной модели в столбце H значительно отличается от исходного сигнала в столбце С .

КОМПЕНСАЦИЯ ПОМЕХ ОТ СОСЕДНИХ СПЕКТРАЛЬНЫХ КАНАЛОВ

Предлагается способ расчета параметров исходных однокомпонентных сигналов и компенсации помех от соседних спектральных каналов путем использования оптимальных комбинаций многокомпонентных сигналов.

Для случая трехкомпонентных сигналов вводится понятие компенсационных коэффициентов, которые обозначены m и n . Компенсация помех в ячейках J11 , O11 и T11 может быть достигнута следующим способом:

J11= G11–H11*m1–I11*n1,(5)

O11= H11–G11*m2–I11*n2,(6)

T11= I11–G11*m3–H11*n3.(7)

Вычисления однокомпонентных сигналов в остальных ячейках столбцов J , O и T могут быть выполнены аналогично по формулам (5, 6 и 7) с теми же компенсационными коэффициентами.

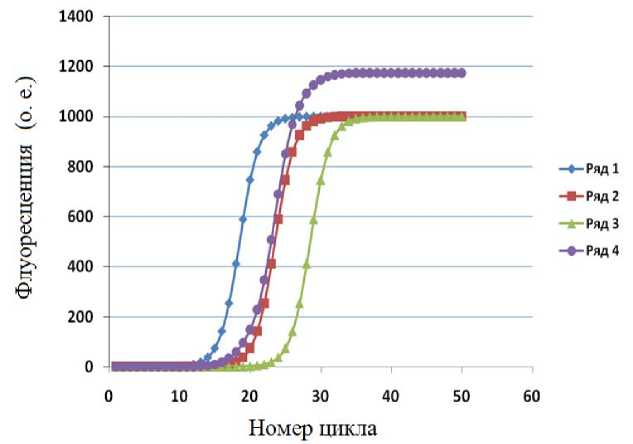
Зависимости модельных сигналов флуоресценции от номера температурного цикла с параметрами, приведенными в таблице.

Ряды 1, 2 и 3 — модельные сигналы с параметрами в столбцах B , С , D .

Ряд 4 — сигнал трехкомпонентной модели в столбце H

ОПРЕДЕЛЕНИЕ ОПТИМИЗИРОВАННЫХ ПАРАМЕТРОВ И ПОСТРОЕНИЕ ВОССТАНОВЛЕННЫХ

ОДНОКОМПОНЕНТНЫХ СИГНАЛОВ

Для вычисления компенсационных коэффициентов и оптимизированных параметров восстановленных однокомпонентных сигналов предлагается использовать аппроксимацию компенсированных сигналов J11:J60 , O11:O60 и T11:T60 сигналами однокомпонентных моделей СФ, предварительно построенных с произвольными параметрами в ячейках E11:E60 , N11:N60 и S11:S60 и оптимизированных при дальнейших расчетах методом наименьших квадратов.

Для оптимизации этих сигналов вычислялись квадраты сигналов ошибок в ячейках:

К11=(J11-E11)^2 ;

P11=(O11-N11)^2 ;

U11=(T11--S11)^2

и в остальных ячейках этих столбцов. Затем вычислялись суммы квадратов сигналов ошибок S k в ячейках:

E10=СУММ(К11:К60) ;

N10=СУММ(P11:P60) ;

S10=СУММ(U11:U60) .

Оптимизированные параметры однокомпонентных сигналов СФ в ячейках E2:E9 (таблица) были получены путем достижения условий минимального значения величин Sk в ячейке E10 при использовании опции "Поиск решения" из меню "Данные". Для этого выполнялись следующие действия: "Установить целевую ячейку E10", "Равной минимальному значению", "Изменяя ячейки E2:E9" и "Выполнить".

Аналогично вычислены оптимизированные параметры однокомпонентных сигналов СФ в ячейках N2:N9 и S2:S9 .

При сравнении исходных параметров моделей СФ в столбцах B , C и D с оптимизированными параметрами в столбцах E , N и S соответственно можно отметить очень малые отличия. Графики, построенные по этим параметрам, также мало отличаются. Основным положительным результатом предложенного способа автоматического восстановления однокомпонентных сигналов является совпадение восстановленных величин C 0 с точностью до 4 знака после запятой (18.5000; 23.4999 и 28.5000).

Аналогичные результаты получены при аппроксимации и оптимизации параметров двухкомпонентных и четырехкомпонентных ПЦР-сигна-лов.

Можно рекомендовать восстановленные величины C 0 использовать в качестве пороговых циклов C _t реальных многокомпонентных сигналов ПЦР, при этом влияние красителей соседних каналов на погрешности измерения будет несоизмеримо малым по сравнению с влиянием шумов и других дестабилизирующих факторов.

ЗАКЛЮЧЕНИЕ

Предложен способ построения модельных сигналов многокомпонентного ПЦР-анализа на основе сигмоидальной функции.

Предложен способ компенсации помех от соседних спектральных каналов. Для этого введено понятие компенсационных коэффициентов, которые используются при аппроксимации комбинаций многокомпонентных сигналов однокомпонентными сигналами.

Предложен способ автоматического определения 8 оптимизированных параметров восстановленных однокомпонентных сигналов. Приведен пример определения этих параметров при аппроксимации трехкомпонентных сигналов.

Показано, что погрешности измерения пороговых циклов за счет влияния красителей соседних каналов не превосходят одной сотой процента единицы температурного цикла.