Многокритериальная оптимизация структуры нейросетевых моделей параллельными генетическими алгоритмами

The problem oftask planning during information processing and control in distributed real-time systems is considered. It is offered algorithm of forming the plan with minimum number of processors. Heuristic algorithms of planning are considered and their relative comparison is presented.

• В.В.    Тынченко

МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ СТРУКТУРЫ НЕЙРОСЕТЕВЫХ МОДЕЛЕЙ ПАРАЛЛЕЛЬНЫМИ ГЕНЕТИЧЕСКИМИ АЛГОРИТМАМИ1

Обсуждается применение эволюционного подхода для построения нейросетевых моделей. Формулируется постановка задачи многокритериальной безусловной оптимизации структуры нейронной сети. Для решения поставленной задачи используются многокритериальные параллельные генетические алгоритмы..

Нейросетевое моделирование является в настоящее время одним из эффективных подходов к решению сложных технических задач, таких как автоматизация процессов распознавания образов, адаптивное управление, аппроксимация функционалов, прогнозирование, создание экспертных систем, организация ассоциативной памяти.

Искусственная нейронная сеть (ИНС) - это набор нейронов, соединенных между собой. С конструктивной точки зрения нейрон - это устройство получения функции нескольких переменных с возможностью настройки его параметров. В общем случае нейрон имеет один выход и несколько входов (синапсов), которые осуществляют связь между нейронами. Математическая модель нейрона имеет следующий вид:

У = f ( ^ ) ,

N

S = S W i- X i , (1)

i = 1

гдеу - величина сигнала на выходе нейрона;/- функция активации нейрона; х- величина сигнала на i-ом входе нейрона; W . - весовой коэффициент i-го входа нейрона.

В соответствии с данной моделью сигнал на выходе нейрона формируется следующим образом: сумматор осуществляет сложение взвешенных входов, а преобра зователь реализует некоторую активационную функцию от выхода сумматора. В общем случае активационная функция является нелинейной, однако практикуют и линейные функции.

Наиболее общим случаем организации нейронов в сеть является многосвязная ИНС, где каждый нейрон может быть связан с любым другим нейроном [1].

Одним из неформализованных моментов практического применения нейросетевого моделирования является выбор структуры ИНС, которая определяется количеством нейронов, их активационными функциями, а также наличием связей между конкретными нейронами. Зачастую структура нейросети выбирается исходя из особенностей решаемой задачи, а также на основе рекомендаций специалиста, имеющего достаточный опыт работы с подобными системами. Автоматизация этого процесса предполагает решение многопараметрической оптимизационной задачи выбора эффективной структуры ИНС.

При решении оптимизационной задачи выбора эффективной структуры ИНС обычно в качестве критерия оценки эффективности нейросетевых моделей используется общая среднеквадратичная погрешность их обучения, которую необходимо минимизировать. При решении ряда задач на основе нейросетевого моделирования требуется выполнение многократных расчетов по нейросетевой модели за короткие промежутки времени, что говорит о целесообразности добавления еще одного критерия оптимизации - оценки эффективности построенной ИНС по вычислительной сложности, которую также необходимо минимизировать.

Формализуем постановку задачи многокритериальной безусловной оптимизации структуры ИНС следующим образом:

E ( C , W , af ) ^ min_, C , W , af

CD ( C , af ) ^ min , .                          c , af-

где E( - ) - общая среднеквадратичная погрешность обучения ИНС; CD(4) - вычислительная сложность ИНС; С - матрица связей ИНС размерности N _s • Nf W- матрица весов связей ИНС размерности N • Nf af - вектор активационных функций на нейронах в ИНС размерности Nf N_h - количество нейронов в ИНС.

Общая среднеквадратичная погрешность обучения ИНС вычисляется по формуле где ТДР) - время обработки одной связи ИНС.

Время ТДР) зависит от вычислительной мощности конкретной вычислительной системы, поэтому для унификации оценки вычислительной сложности ИНС перейдем к безразмерным величинам, не зависящим от времени. Для этого разделим обе части выражения (6) на ТДР):

cd ⁽ C , ^af , P ) = N _С в ( C ) + X      ^{( af} , P ) .     (7)

T ^св ( P )                     Т ^св ( P )

Обозначим CD ( C , af ) = cd ⁽ C ^{, af ,} P ) T ^св ( p )

.

Введем не зависящий от аппаратной реализации коэффициент относительной сложности вычисления активационной функции на .-м нейроне как

,    т ^акт ( af , p )

K i ( af ) = —--------, тогда критерий оценки вычисли

Т ^св ( P )

тельной сложности нейросетевой модели примет окончательный вид

N и CD (C, af) = NСв (C) + X Ki (af).

= 1

E ( C , W, af ) =

m

X\

j = 1 ’

X ( OUT k ( C , W , af ) - y j ) k = 1

n

m

где OUT k ( C , W , af ) - реальное значение k-го выхода ИНС, имеющей структуру ( C , W , af ) при подаче на ее входы_/-го образа; у ^ - идеальное (желаемое) выходное состояние k-го нейрона; п - количество нейронов на выходе сети; т - размер обучающей выборки.

Вычислительная сложность нейросетевой модели напрямую зависит от временных затрат на обработку всех связей нейросети и на вычисление активационных функций на каждом нейроне, поэтому представляется логичным оценивать вычислительную сложность ИНС следующим образом:

_    N. (C)         Nи    _ cd(C, af, P) = X Тв (C, P) + X TaKT (af, P), (4) i=1                   i=1

где N ( • ) - количество связей ИНС; Т“б) - время обработки .-ой связи ИНС; Т™^) - время вычисления активационной функции на .-ом нейроне; N - количество нейронов ИНС; Р- производительность вычислительной системы.

Под временем обработки одной связи ИНС понимается время добавления веса данной связи к сумме весов уже обработанных ранее связей на входе конкретного нейрона:

n+1

Т™ (C, P) = Т (X Wy) - Т (X Wy),(5)

j=1

где Т(х) - время вычисления х; w . - .-ый вход/-го нейрона; п = 0,1,2,... - количество обработанных связей.

Время обработки одинаково для всех связей и определяется программной и аппаратной реализацией ИНС. Тогда формула (4) примет вид

_              Nи   _ cd (C, af, P) = Nсв (C) • Tсв (P) + X Т (af, P), (6)

= 1

Для решения многокритериальных задач оптимизации существует ряд классических методов, однако они плохо подходят для решения сложных задач в силу следующих присущих этим методам недостатков:

• -    некоторые методы могут быть чувствительны к характеру формы Парето-оптимального фронта;

• -    может требоваться некоторая дополнительная информация, которая чаще всего неизвестна;

• -    для получения Парето-оптимального множества требуется несколько независимых друг от друга циклов оптимизации, согласование которых может вызвать чрезмерное количество вычислений.

Вследствие этого для решения многокритериальной оптимизационной задачи выбора эффективной структуры ИНС предлагается применить эволюционный подход, позволяющий преодолеть сложные моменты, возникающие при использовании классических методов. Эволюционные алгоритмы обеспечивают глобальный просмотр пространства поиска решений, позволяют избегать локальных минимумов и получать много альтернативных решений за один цикл оптимизации.

Эволюционный подход к проектированию структуры ИНС можно разбить на два этапа.

На нервом этане осуществляется выбор соответству-

ющей схемы представления структуры нейросети. Ин формация о структуре может непосредственно кодиро-

^в

I -

ваться в виде двоичных последовательностей, т. е. каждая связь и каждый узел (нейрон) прямо специфицируется

определенным количеством битов. Такой способ представления называется схемой непосредственного коди-

^в

^в

рования (сильная схема спецификации). В данной схеме каждая связь нейронной сети непосредственно задается ее двоичным представлением. Матрица С размерностью п • п, С = [с] _п , _п может представлять связи нейронной сети, состоящей из п узлов (нейронов), причем значение ^.определяетналичие или отсутствие связи между .-ым и/-ым нейронами. Если с = 1, то связь существует, если с..= 0, то связь отсутствует При таком подходе двоичная

последовательность (хромосома), представляющая связи нейронной сети, имеет вид комбинации строк (или столбцов) матрицы С. Если принимать во внимание лишь однонаправленные связи, это позволит учитывать только те элементы матрицы С, которые задают связи данного узла (нейрона) со следующими узлами. Кроме этого, хромосома должна содержать информацию о виде активационной функции на каждом нейроне. Информацию об активационной функции можно добавлять в конец последовательности бит соответствующего нейрона.

Второй этан включает в себя выполнение пяти шагов.

• 1.    Декодирование каждой особи текущей популяции для описания структуры нейронной сети.

• 2.    Обучение каждой нейронной сети, имеющей структуру, полученную на первом шаге. Обучение ИНС с заранее определенной структурой является многопараметрической задачей оптимизации, которая заключается в поиске оптимального набора весов связей нейросети. Для решения данной задачи также целесообразно использовать эволюционный подход [1; 2]. В генетических алгоритмах веса кодируются в виде двоичных последовательностей (хромосом). Каждая особь популяции характеризуется полным множеством весов нейронной сети. Оценка приспособленности особей определяется функцией приспособленности, задаваемой в виде суммы квадратов погрешностей, т. е. разностей между ожидаемыми (эталонными) и фактически получаемыми значениями на выходе сети для различных входных данных.

• 3.    Оценивание приспособленности каждой особи (закодированной структуры ИНС).

• 4.    Репродукция особей, согласно выбранному способу селекции.

• 5.    Применение генетических операторов скрещивания и мутации для получения нового поколения.

В отличие от однокритериальной оптимизации, где целевая функция и функция пригодности часто идентичны, при решении многокритериальной задачи необходимо так производить назначение пригодностей и отбор, чтобы достичь Парето-оптимального множества. Различаются эволюционные методы, где критерии рассматриваются отдельно, подходы, основанные на классическом методе уплотнения, и методы, напрямую использующие концепцию доминирования по Парето. К последней группе методов относится широко известный эволюционный метод многокритериальной оптимизации FFGA (Fonseca and Fleming’s Multiobjective Genetic Algorithm) [3], который представляет собой основанную на Парето-доминировании процедуру ранжирования индивидов, где ранг каждого индивида определяется числом доминирующих его индивидов.

Назначение пригодности в FFGA осуществляется в соответствии с нижеследующим алгоритмом [3].

Вход: P_t (популяция).

Выход: F (значения пригодности).

Шаг 1. Для каждого i OP вычисляют его ранг:

г(> 1 + I {/ I j G P^j i}S, где символ | ■ | обозначает мощность множества. Индивид, чей вектор решения недоминируем относительно P имеет ранг 1.

Шаг 2. Популяция сортируется согласно рангу г. Каждому i g P_t назначается сырая пригодность F'(i), интерполируя от лучшего (r(i) = 1) к худшему индивиду (r(i) <  N).

Шаг 3. Вычисляются значения пригодностей F(i) усреднением значений сырой пригодности F'(i), среди индивидов i О P с идентичным рангом r(i) (выравнивание пригодностей в целевом пространстве).

Поскольку выполнение расчетов по адаптивным поисковым алгоритмам занимает большое количество времени, для решения задачи выбора эффективной структуры ИНС целесообразно применить параллельные генетические алгоритмы (ПГА) и выполнять вычисления одновременно на нескольких независимых вычислительных устройствах. Данный подход позволит значительно повысить быстродействие и улучшить качество найденных решений.

Различия в способах распараллеливания генетического алгоритма определяются особенностями реализации основных этапов алгоритма:

• -    способом оценивания пригодности индивидов;

• -    способом реализации операторов мутации, селекции и скрещивания;

• -    количеством независимо эволюционирующих популяций (субпопуляций);

• -    способом реализации оператора миграции при наличии нескольких субпопуляций.

Наиболее распространенными и значимыми являются следующие два способа: ПГА с распределенной оценкой пригодности (Master-Slave PGA) и мультипопуляци-онные ПГА [4].

ПГА с распределенной оценкой пригодности использует единственную популяцию, которая разбивается на группы по числу доступных процессоров, и индивиды каждой группы оцениваются на отдельном процессоре (в идеале - один индивид на один процессор). Селекция и скрещивание носят глобальный характер, т. е. каждый индивид может конкурировать и скрещиваться с любым другим индивидом из популяции.

В мультипопуляционных ПГА популяция делится на субпопуляции, каждая из которых эволюционирует изолированно от всех других (географическая изоляция). Периодически некоторые индивиды перемещаются от одной субпопуляции к другой (мигрируют). Для реализации механизма миграции вводится дополнительный оператор - оператор миграции, определяющий следующие параметры:

• -    топологию связи между субпопуляциями (гиперкуб, тор, двумерная или трехмерная решетка и т. п.);

• -    скорость миграции (количество перемещаемых индивидов);

• -    схему миграции, т. е. способ отбора индивидов для перемещения в другую популяцию («лучшие», «худшие», отобранные случайным образом) и способ отбора замещаемых индивидов («лучшие», «худшие», отобранные случайным образом);

• -    миграционный интервал, определяющий частоту перемещения (если интервал постоянный - синхронная миграция, если интервал может изменяться в зависимости от некоторого события - асинхронная миграция).

В рамках данной работы была реализована клиент-серверная программная система, позволяющая автоматизиро- вать процесс выбора эффективной структуры ИНС с использованием многокритериального ПГА. В качестве многокритериального генетического алгоритма в программной системе используется FFGA. Программная система предоставляет пользователю следующие возможности:

• - устанавливать параметры генетического алгоритма настройки весов связей ИНС (объем популяции, генетические операторы, количество итераций и т. д.), а также изменять эти параметры в ходе работы программы;

• -    изменять параметры генетического алгоритма при выборе эффективной структуры ИНС (объем популяции, генетические операторы, количество итераций и т. д.), а также изменять эти параметры в ходе работы программы;

• - устанавливать параметры параллельного генетического алгоритма (топологию связи между субпопуляциями, скорость и схему миграции, а также миграционный интервал);

• -    отслеживать в ходе работы программной системы построение графиков пригодности лучшего и худшего индивидов популяции, а также средней пригодности популяции при настройке весов ИНС;

• -    отслеживать в ходе работы программной системы количество недоминируемых индивидов популяции, а также построение графиков средней пригодности популяции и пригодности худшего индивида популяции при выборе эффективной структуры ИНС.

Разработанная программная система была использована для выбора эффективной структуры ИНС, а также весов связей при решении практической задачи моделирования процесса рудно-термической плавки [5].

В качестве параметров, характеризующих эффективность работы печи рудно-термической плавки, были выбраны такие параметры, которые характеризуют процесс с различных сторон, т. е. позволяют оценить технологические, энергетические и экономические аспекты. К ним относятся потери цветных металлов с отвальными шлаками (CNI); производительность (П); удельный расход электроэнергии (^_у); температура шлака (Т); выбросы вредных веществ в атмосферу (С_гю) и другие.

В связи с высокой температурой и агрессивной средой в печи трудно получить непрерывную, надежную и полную информацию о процессе, поэтому выбор управляющих параметров обусловлен не только их весомым влиянием на процесс, но и возможностью получения непрерывной, достоверной информации о них. На основании этого в качестве основных управляющих воздействий используются электрические параметры и загрузка шихты по отдельным составляющим: количество загружаемого в печь агломерата (G ); количество загружаемого в печь кремнезема (G_sio2); количество загружаемого в печь кокса (О_С); количество загружаемого в печь конвертерного шлака (О ); ввод электрической мощности (Р); заглубление электродов (Н) напряжение (U) и другие.

При этом химический состав загружаемого агломерата и химический состав конвертерного шлака были приняты постоянными.

Размерность вектора входных воздействий на процесс равна 10, вектора выходных параметров также составляет 10. Для проведения экспериментов использовалась выборка из 47 точек [5].

При решении задачи нейросетевого моделирования процесса рудно-термической плавки использовалась сеть из пяти однотипных персональных компьютеров с процессорами Athlon64 3200+.

При решении задачи были выбраны следующие параметры мультипопуляционного ПГА:

• - размер популяции (20 индивидов);

• -    количество поколений (30);

• - турнирная селекция (3 индивида в турнире);

• -    равноточечная рекомбинация;

• -    средняя мутация;

• -    максимальное количество скрытых нейронов (10);

• -    топология связи между субпопуляциями (каждая с каждой);

• -    скорость миграции (2 индивида);

• -    синхронная миграция с интервалом в 3 поколения;

• -    схема миграции (для перемещения случайным образом отбираются недоминируемые индивиды; замещаются индивиды с наименьшим значением функции пригодности).

Список используемых активационных функций и соответствующих им коэффициентов относительной сложности вычисления приведен в таблице.

В результате решения данной задачи была получена аппроксимация Парето-множества - множество из 16-ти нейросетевых моделей с ошибкой настройки от 3,42 до 3,74 % и вычислительной сложностью, лежащей в пределах от 357,04до 369,27.

Приближение фронта Парето на последнем поколении генетического алгоритма представлено на рисунке.

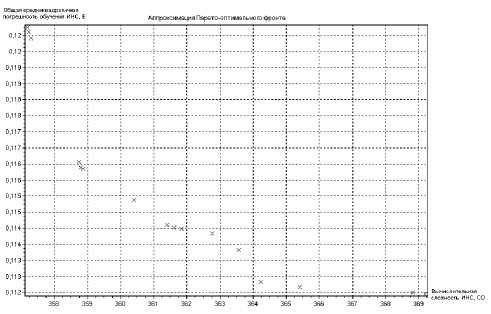
Аппроксимация Парето-оптимального фронта для задачи моделирования процесса рудно-термической плавки

Полученные результаты свидетельствуют об эффективности применения эволюционного подхода для автоматизации нейросетевого моделирования, при этом разработка и внедрение параллельных генетических алгоритмов позволит значительно ускорить процесс построения нейросетевых моделей, повысить их качество и предоставить возможность выбора нейросетевой модели из множества альтернатив, исходя из требуемой точности и имеющихся вычислительных ресурсов.