Многокритериальное моделирование процессов и конструкции камеры смешения пароструйного эжектора конденсационной турбины

Значительная часть методов исследования объектов отечественной теплоэнергетики и их элементов не вполне учитывает факторы, влияющие на работу эжектора. Нами выбрано направление изучения процессов повышения энергетической эффективности часто применяемых пароструйных эжекторов ЭО-50 (рис. 1) конденсационных турбин ВКВ-22-1.

Принцип действия эжектора заключается в том, что пар, подаваемый к эжектору, поступает по паропроводу 2 к соплу 3. При этом скорость пара после сопла достигает 800–1000 м/с. Теплоноситель проходит через камеру всасывания, которая соединяется с патрубком 1 подвода воздуха из конденсатора. Поступающий из конденсатора воздух увлекает за собой пар, образуя при этом паровоздушную смесь. Она проходит через диффузор 4 (скорость смеси резко падает, а давление повышается) и попадает на трубки 5 охладителя, по которым прокачивается холодный конденсат турбины. Образовавшийся в охладителе конденсат рабочего пара удаляется из корпуса эжектора че- рез дренажный трубопровод, а воздух поступает во вторую ступень эжектора. После второй ступени воздух с давлением несколько выше атмосферного выбрасывается в помещение машинного зала. Конденсат турбины поступает в камеру 8 и проходит через камеру 7 в подогреватели низкого давления.

В расчетах рабочих характеристик эжекторов обычно осуществляется оптимизация на основе моделирования по отдельным критериям. Например, так моделируют процессы эксплуатации паротурбинного оборудования с пароструйным эжектором, имеющим конструкцию камеры смешения, которая предотвращает лишь срыв потока смеси газов.

Такой подход позволяет незначительно повысить КПД эжектора (до 1,5 %), коэффициент скорости потока (до 2,5 %), снизить расход рабочего пара (до 32,3 %), уменьшить размеры камеры смешения и повысить срок службы от 20 до 40 лет [1].

Возможности применения инновационных методов моделирования процессов паротурбинного оборудования обусловлены развитием методов

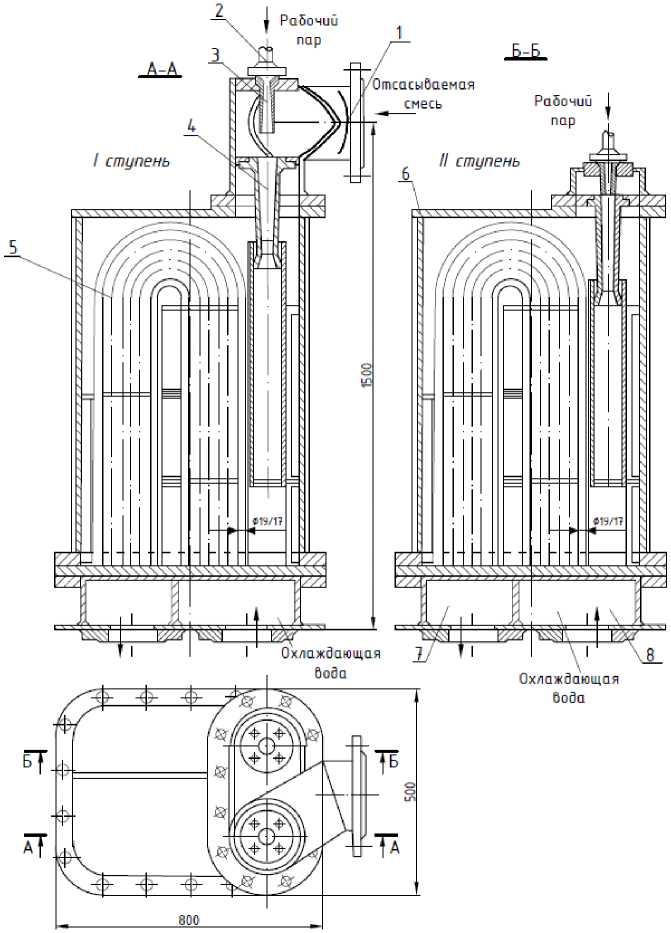
Рис. 1. Схема двухступенчатого пароструйного эжектора: 1 – патрубок подвода воздуха из конденсатора; 2 – паропровод; 3 – сопло; 4 – диффузор;

5 – трубки охладителя; 6 – корпус; 7 и 8 – выходная и входная водные камеры

теори и и пра кти ки газ од ин ам и чес к и х ра с че тов . К роме того, а на л из ре зу л ьта т ивнос т и м е тодов применительно к эжектор а м конд ен са ц ион ны х турбин показал необходимость р а с шире н ия числ а крите риев оп ти м а л ьнос т и при ре г у лиров а н ии пар а м е тров проце с с ов и ге ом етрии ко нс тр у кц и и. Э то подтв е р ж да е т оте че с т в е н ны й опы т конс тр у иров ани я кам е р с м е ше ния и повыше ни я эффе кт ив ности работы агр е га тов , ис пол ьзующи х м ногос т у пе нчатые пароструйные эжекторы. Не ре г у л ир у е м ое по крите ри ям эффе кт ивнос ти из м е не н ие пл ощади се че ни й горл ов и н ка м е р с м е ше ни я (пе рв ой и п осл е д у ющей с т у пене й) (с м . рис . 1) поз в ол ил о д опол н ител ь но пов ыс и ть К П Д па рос тр уй ны х эж е кторов лишь до 7,8 % [1–3].

Также необходимо рассмотреть на принципиальной схеме работы струйного аппарата на рис. 2 принцип движения потоков сред, поступающих в камеру смешения. Из сопла А поступает рабочий пар (поток) и патрубка подвода воздуха из конденсатора поступает инжектируемый поток, вместе они поступают в камеру смешения В – конфузор и диффузор. В камере смешения происходит выравнивание скоростей с повышением давления паровоздушной смеси. Из камеры смешения В и конфузор поток поступает в диффузор, где происходит дальнейший рост давления. Получается, что давление смешанного потока на выходе из диффузора выше давления инжектируемого потока, поступающего в приемную камеру.

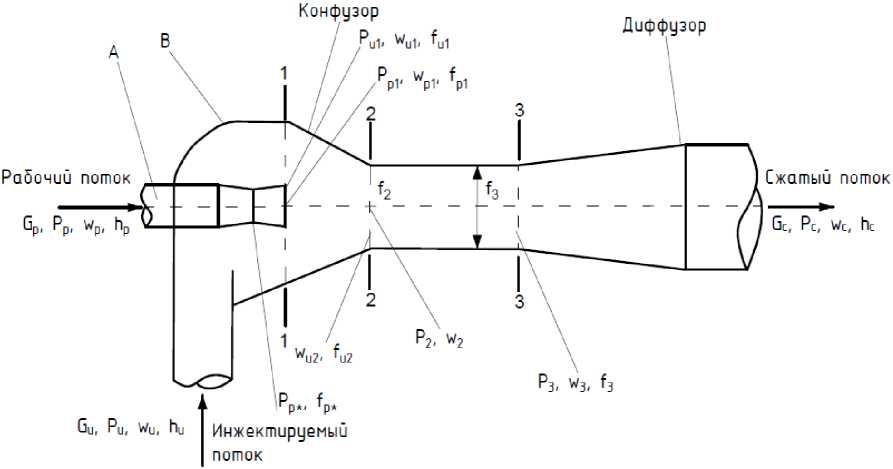
Рис. 2. Принципиальная схема работы струйного аппарата: А – сопло для подачи рабочего пара; В – камера смешения; 1, 2, 3 – сечения для расчета эжектора

Актуальность темы исследования

Актуальность м н огокрите р иа л ь ного м оде л ирования эле м е нтов п арот ур би н ного обор удов ани я в ц и ф ров ом и физ иче ском пре дс та вл ени и обос но в ан а не об х од им ос тью пов ы ше ни я эне рге т иче с кой и э к ол оги чес кой эффект ивн ос ти в кон це п ци и циф р овиз ац и и м ет од ов устойч и в ого ра з в ит ия стран ы и р е ги она . Э та концеп ци я з акл юча етс я в обеспече ни и по тре бнос тей б у д у щ и х покол ени й в э не рго сб ере ж е н ии м е то да м и, ускоряющими при н яти е р е ше ни й в прое ктах и пл ана х . Пр и этом с л е д у е т у ч е с ть по л ож и те л ь ны й з а ру беж ны й опыт ко нс т р у и ров а н ия эл ем е н тов те п л оэне рге ти к и и те п л о техн и ки по отде л ь ным кри т ери ям оп тимальности – да в л е н и е в с а с ыв ани я, коэффиц ие н т и нж ек ци и и площадь камеры смешения [1, 2].

Постановка задачи исследования

Несоответствие состояния отечественной теплотехники современным требованиям и факторам-вызовам многокритериальности оценки приводит к снижению энергетической эффективности. Для большего повышения энергетической эффективности турбинного оборудования, сравнимого с достижениями развитых стран мира, необходимо решить следующие проблемы: чрезмерное снижение энергетической эффективности турбины вследствие присосов воздуха в уплотнениях турбины (до 5 %) [1, 3]; снижение КПД конденсационных турбин ВКВ-22-1 (до 2 %) из-за срывов потока паровоздушной смеси [1, 2, 4]; повышенные затраты на ремонт турбины и эжектора из-за неоптимальной площади сечения камеры смешения в эжекторе [3]. Недостаточная степень решения указанных проблем эжекторов определила цель работы – выявить и исследовать на основе многокрите- риального моделирования процессов повышения энергетической эффективности эжектора турбины при интегральном применении системы критериев оптимальности в оценках трех параметров: минимизация отклонения вакуума в конденсаторе, давления всасывания и расхода пара при регулировании проходного сечения камеры смешения пароструйного эжектора по показателям энергоэффективной площади [5]. Для достижения цели решены следующие задачи оценки газодинамических процессов в паровом эжекторе: анализ влияния методов моделирования процессов повышения энергетической эффективности пароструйных эжекторов паротурбинного оборудования; совершенствование газодинамических расчетов применением трех и более критериев оптимизации; разработка методики совершенствования газодинамических расчетов для обоснования эффективных параметров камеры смешения.

Теоретическая часть

Для оценки влияния методов моделирования на энергетическую эффективность пароструйных эжекторов конденсационных турбин использованы стандартные газодинамические расчеты. Авторы исходили из гипотезы, что использование многокритериального подхода к моделированию системы методов и процессов позволит более значительно повысить возможности увеличения энергетической эффективности исследуемого оборудования. Опыт развитых стран и наши расчеты показали влияние на этот показатель увеличения числа критериев оптимальности. Кроме того, повышаются качество конструирования и возможности регулирования процессов эксплуатации оборудования, спроектированного таким образом. Проблема снижения КПД турбины ВКВ-22-1 до 1,5–2 % из-за срывов потока паровой смеси обычно решается известными типовыми методами [4, 6]. Повышенные затраты на ремонт турбины и эжектора появляются по факторам неоптимальной площади камеры смешения в эжекторе и поставок некачественных запчастей. Это ведет к простоям оборудования, усугубляемым высоким моральным и физическим износом (в том числе из-за нерегули-руемости проходных сечений камеры смешения). Возможности применения инновационных методов ограничиваются также недостаточностью финансирования, усилением влияния экономического кризиса и санкций. Срок службы оборудования при этом снижается до 15–25 лет. Из типовых стандартных методов газодинамических расчетов при моделировании использовались следующие: построение расчетных рабочих характеристик пароструйного эжектора с использованием нормативов эксплуатации оборудования и одного критерия оптимальности процессов; применение численных методов моделирования для решения нелинейных дифференциальных уравнений и другие [1, 7, 8]. Анализ указанных библиографических источников показал, что такие методы во многом решают поставленные проблемы. Однако моделирование на их основе обусловливает ряд проблем: низкая точность и чрезмерная сложность расчетов; возможность проявления собственных свойств модели из-за несоответствия критериев подобия объекта и модели; необходимость применения особых контрольно-измерительных приборов на физической модели или объекте; относительная сложность построения модели; трудности достоверной экстраполяции результатов на другие масштабы из-за отсутствия надежных критериев достоверности масштабного перехода. Несмотря на перечисленные недостатки, цифровое, или математическое и физическое моделирование часто служит единственным методом исследования. В данном случае цифровой симулятор физической модели применен для верификации результатов математического моделирования процессов эжекции [9]. Инновационные методы многокритериального моделирования позволяют получить более значительное повышение энергетической эффективности. Оптимальное решение, основанное на современных достижениях теории газодинамических процессов, отличается возможностями описания статики и динамики взаимосвязанных процессов моделируемого симулятора объекта. Расширение числа показателей и критериев, оценивающих связанные процессы, повышает качественные и количественные возможности направлений повышения энергетической эффективности проектируемой конструкции теплотехнического оборудования [7, 8]. На этапах эксплуатации необходимо обеспечить регулируемость процессов с использованием дополнительной информации по прямым и обратным связям методов. Многокритериальная модель и предлагаемая система критериев расширяют возможности регулирования обратной связи не только между методами, но и между расчетной моделью симулятора и физической моделью. Дополнительные эксперименты приводят к уточнению системы моделей, углублению знаний об этом явлении, к постановке новых экспериментов [7, 8].

Научная часть

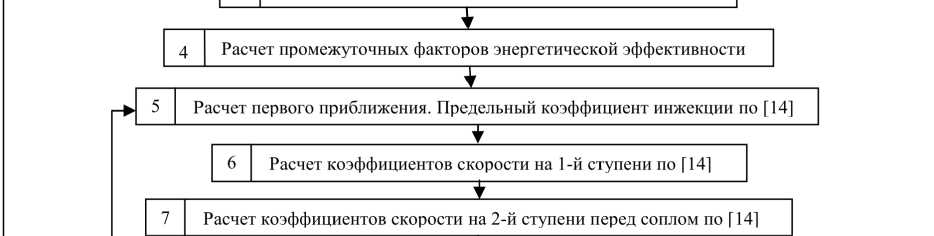
Методика расчетов может быть отображена моделью многокритериальной оптимизации параметров реализации газодинамических процессов в пароструйном эжекторе конденсационной турбины (рис. 3). Многокритериальность предлагается обеспечить на основе комбинирования стандартных (типовых) методов расчета в многокритериальной модели. Для этого применяется численное моделирование процессов образования паровоздушной смеси газов в эжекторе исследованием взаимосвязи показателя-свойства энергетической эффективности и факторных параметрических показателей. Методика расчета и моделирования процессов представлена моделью алгоритмического вида на рис. 3. Использование ее прямых и обратных связей (по условиям 2, 10, 13 и 16) позволит оценить повышение энергетической эффективности по показателю увеличения КПД в итоге оптимизации. Выбрана система трех критериев, измеряемых термодинамическими и геометрическими параметрами минимизации: давление всасывания; расход пара и термодинамических параметров потоков; площадь эффективной камеры смешения, регулируемая по указанным параметрам. Они определяют обоснованные направления совершенствования камер смешения эжекторов. Моделирование геометрических характеристик сопел камеры смешения эжектора позволяет регулировать указанные параметры в необходимом диапазоне. Особенно это актуально для эжекторов конденсационных установок, так как в процессе эксплуатации могут изменяться такие параметры, как расходы и температуры подсасываемой паровоздушной смеси и циркуляционной воды. Поэтому требуется разработка обоснованной регулируемой геометрии камеры смешения в конструкциях таких установок. Под регулированием геометрии камеры смешения понимается возможность изменять основные геометрические характеристики – отношение площадей входных сечений сопел для эжектирующего и эжектируемого сред α = f ₁/ f ₂ в последовательности этапов алгоритма, как цифровой модели процессов конструирования и функционирования эжектора (см. рис. 3) с учетом критического режима работы эжектора. Критический режим работы эжектора – переход от сверхзвуковой скорости к дозвуковой скорости, который достигается при помощи скачков уплотнения для обеспечения наиболее выгодного режима работы пароструйного эжектора.

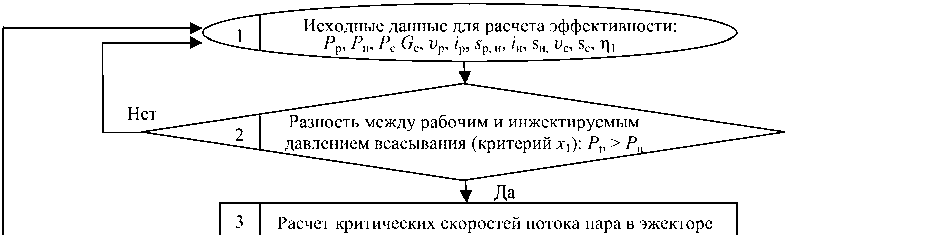
Разность между рабочим и инжектируемым давлением всасывания (критерий лу): Р_р > Р.

Исходные данные для расчета эффективности:

^р, ^н, Pc ^cs Пр, Zp, Sp. „, (_и, S_n V_o S_c, Ц ।_____

Нет

3	Расчет критических скоростей потока пара в эжекторе

4	Расчет промежуточных факторов энергетической эффективности

5	Расчет первого приближения. Предельный коэффициент инжекции по [14]

6	Расчет коэффициентов скорости на 1-й ступени по [14]

7	Расчет коэффициентов скорости на 2-й ступени перед соплом по [14]

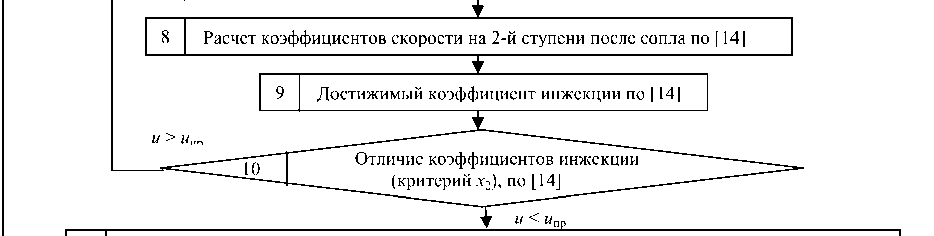
Отличие коэффициентов инжекции (критерий х2), по [14]____

8	Расчет коэффициентов скорости на 2-й ступени после сопла по [14]

9	Достижимый коэффициент инжекции по [14]

11	Расчет расхода рабочего пара, площади камеры смешения и энтальпии сжатого потока по [14]

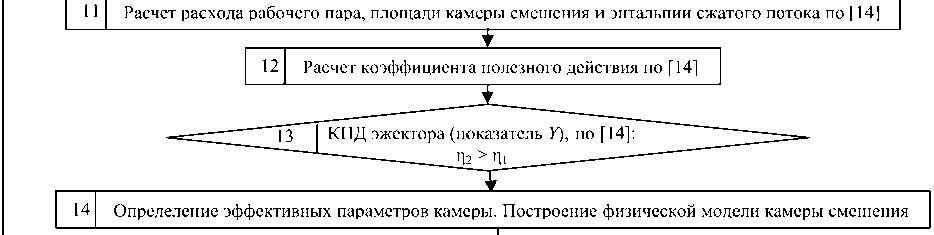
КПД эжектора (показатель У), по [14]

12	Расчет коэффициента полезного действия по [14]

14	Определение эффективных параметров камеры. Построение физической модели камеры смешения

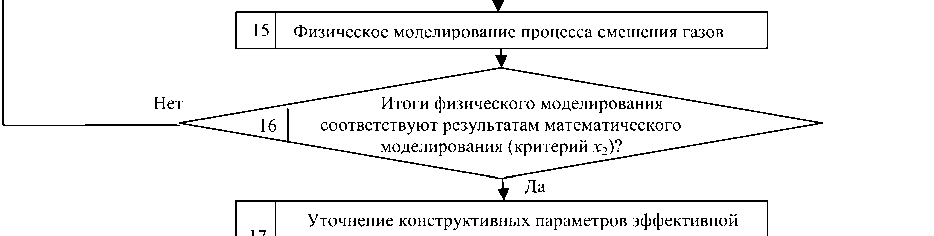
Итоги физического моделирования соответствуют результатам математического ----^моделирования (критерий х2)?___——■

Нет

15	Физическое моделирование процесса смешения газов

17	Уточнение конструктивных параметров эффективной камеры смешения

18	Проектирование усовершенствованной камеры смешения методом многокритериального моделирования

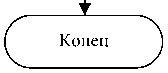
Рис. 3. Цифровая модель многокритериальной оптимизации параметров камеры смешения пароструйного эжектора

• 1.    Определение характеристики эжектора. Исходными данными для построения характеристики эжектора являются параметры, которые определяют скорость звука в рабочем паре (α_р*) и инжектируемом потоке (α_и*).

• 2.    Оценка условия между давлением рабочим и инжектируемым всасывания ( P _p >  P _и). Затем рассчитываются относительные давления ( Р _и / Р _р ) по формуле (1).

• 3– 8. Расчеты стандартных факторов и коэффициентов для определения по формуле (1) предельного коэффициента инжекции u пр .

• 9.    Оценка достижимого коэффициента инжекции по формуле (2).

• 10.    Проверка условия: если оно верно, то необходимо переходить ко второму этапу методики.

• 11,    12. Расчет условия 13 для определения КПД эжектора (показатель-свойство Y как цель повышения энергетической эффективности эжектора) по формуле (3).

Далее переходим к третьему этапу – условие 14 и 15, в которых необходимо определить расход рабочего пара по формуле (4) и эффективные параметры камеры смешения по формуле (5). На заключительном этапе необходимо сопоставить результаты физического и математического модели- рования. Их совпадение позволяет уточнить ре- альные параметры камеры смешения, корректировать указанные параметры, полученные при расчете. В итоге повышается обоснованность конструи- рования и регулирования геометрии камеры смешения. Моделирование процессов регулирования геометрии камеры является предметом дальнейших исследований. В газодинамических расчетах используются известные исходные данные рабочих эжекторов ЭО-50, ЭО-50М и формулы [10–15], сведенные в табл. 1. Дополнительно введены критерии в блок-схеме расчета (рис. 4):

Y – показатель энергетической эффективности паротурбинного оборудования, а x_n – это показатели-факторы (причины, вызывающие проблемы):

• x ₁    – давление всасывания в эжектор ( P _p >  P _н), где P _p – насыщенный рабочий пар перед эжектором, Па; P _н – инжектируемый насыщенный пар, Па. Определим критерий х ₁ по формуле (1).

Опишем уравнением (1) рабочий участок характеристики работы пароструйного эжектора P н = f ( u ) в диапазоне давлений всасывания от P н , которому соответствует u = 0, до P н = P р1 :

u

пр

f 3     ¹ ) k н П н* a p* P u

Ц

( f ,.   q рн J k p П р* a н* P p

Таблица 1

Газодинамический расчет рабочих эжекторов ЭО-50 и ЭО-50М по критериям оптимизации (дополненная часть расчетов) по алгоритму рис. 3

Показатели по этапам алгоритма	Обо-значения	Размерность	Формулы расчета	Результаты расчета
				Стандартный метод		Многокритериальный метод
1	2	3	4	5	6	7
1. Исходные данные	u p i р s р	м3/кг кДж/кг кДж/(кг·К)	По табл. 1 [13]	0,32 2756 6,76	0,32 2756 6,76	0,32 2756 6,76
	U u i и s и	м3/кг кДж/кг кДж/(кг·К)	По табл. 1 [13]	26,4 2564 8,35	26,4 2564 8,35	26,4 2564 8,35
	U c s с	м3/кг кДж/(кг·К)	По табл. 1 [13]	5,11 7,77	5,11 7,77	5,11 7,77
2.Расчет критических скоростей потока пара в эжекторе по критерию х 1	α р*	м/с	По формуле 1.2 [14]	442	451	395
	α и*	м/с	По формуле 1.2 [14]	380	389	367
3. Расчет промежуточных факторов энергетической эффективности	Vo	–	^yo _ a u* a p*	0,8597	0,86	0,964
	1 Ve	–	1 Ve	1,16	1,16	1,037
	П р2 =П р и	–	По формуле 2.2 [14]	0,0083	0,009	0,009
	λ ри	–	По газодинамическим таблицам П2 [13]	2,63	2,62	2,67
	q ри	–	По газодинамическим таблицам П2 [13]	0,0652	0,066	0,0759

Окончание табл. 1

1	2	3	4	5	6	7
Расчет первого приближения
4. Расчет первого приближения. Определение предельного коэффициента инжекции	λ с3	–	Принимаем по газодинамическим таблицам П2 [13]	0,57	0,562	0,594
	q с3	–	Принимаем по газодинамическим таблицам П2 [13]	0,793	0,785	0,815
	П с3	–	Принимаем по газодинамическим таблицам П2 [13]	0,84	0,844	0,827
	u пр	–	По формуле 2.32 [14]	0,289	0,296	0,395
	q и2	–	По формуле 2.30 [14]	0,659	0,661	0,658
	λ и2	–	По газодинамическим таблицам П2 [13]	0,446	0,448	0,453
4. Расчет первого приближения. Определение предельного коэффициента инжекции	П и2	–	Принимаем по газодинамическим таблицам П2 [13]	0,899	0,899	0,904
	П с2	–	Аналогично по формуле 2.2 [15]	0,157	0,157	0,157
5. Расчет коэффициентов скорости на 1-й ступени	К 1	–	По формуле 2.20 [14]	0,834	0,834	0,834
	К 2	–	По формуле 2.21 [14]	0,812	0,812	0,812
6–7. Расчет коэффициентов скорости на 2-й ступени	К 3	–	По формуле 2.22 [14]	1,784	1,8	1,159
	К 4	–	По формуле 2.23 [14]	8,841	8,979	7,229
8. Достижимый коэффициент инжекции	u	–	По формуле 2.24 [14]	0,282	0,296	0,394
9. Отличие коэффициентов инжекции по критерию х 2	δ u	%	u - u np 5 u =-------p-- 100% 0,5 ■ ( u + u пр )	2,5	0,2	0
u <  u пр – расчеты выполнены верно и соответствуют условию 9
10. Определение расхода рабочего пара	G р	кг/с	G p = 1 + u	6,08	4,86	3,08
10. Определение площади камеры смешения и энтальпии сжатого потока	f *	м 2	G„ ■a.      , f = —p-- 10 - 3 k ■ П * ■ Р 0	7,644	6,24	3,59
	f р	м2	=     G p ■%* --10 - 3 p k ■ Пр* ■ Р р ■ q p2	0,073	0,054	0,030
	f и	м2	f =--- G ulOn*-- 10 - 3 и k ■ П и* ■ Р и ■ q и2	0,081	0,06	0,033
	f 2	м 2	f 2 = ( f , + f и ) ■Ю- 3	0,154	0,144	0,063
	f 3	м2	=--- G ^0 *--10 - 3 J3    ₽■ k ■ Пс * ■ Р с ■ q C 2	0,05	0,041	0,0297
	i c	кДж/кг	.     i p + u ■ i и 1 c =    1 1 + u	2709,9	2708,3	2698,2
11–16. Расчет коэффициента полезного действия. Проверяем условия 13, 14, 16 по критерию х 3 . Затем приступаем к конструированию усовершенствованной камеры смешения, пункты 17–18	η	%	u ■ ( ic — i i — Tq c ■ ( ^ c — % ) ) n =    —и—o.c.vjc—И/У ■ 100 % i p — i c — T o.c. ■ ( s p — s c )	25,8	26,9	33,6

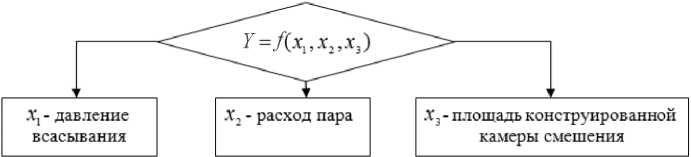
Рис. 4. Блок-схема расчета математической модели исследования объектов

где Р _c – давление сжатого воздуха на выходе из эжектора, Па;

Р _и – давление инжектируемого пара, Па;

f * =

G p - a *

k ■ П * ■ Р 0

■ 10 - ³ ,

Р _p – давление рабочего пара, Па [14].

где G _р – массовый расход рабочего пара, кг/с;

a * - местная скорость звука;

x ₂ – расход пара на турбину и эжектор, а также термодинамические параметры рабочего, ин-

жектируемого и смешанного потоков, в данном случае отличие коэффициентов инжекции (δ u ) по формуле (2). Из формулы (1) определяем отличие коэффициентов инжекции по формуле (2)

k – показатель адиабаты, k = 1,13;

П* – относительное давление потока;

Р ₀ – насыщенный рабочий пар перед эжектором, Па [14].

5 u =

I u - u пр I

0,5 ■ (u + uпр)

■ 100%,

где u _пр – предельный коэффициент инжекции;

u – достижимый коэффициент инжекции [14].

x ₃ – площадь конструируемой камеры смешения усовершенствованного (наиболее эффективного) эжектора. Данные показатели-факторы помогают нам наглядно на рис. 3 определить, от чего зависит показатель энергетической эффективности (КПД) данного объекта исследования. Проверяем условия 13, 14, 16 по критерию х 3 – КПД эжектора (η, %), расхода рабочего пара ( G р , кг/с) и площади камеры смешения ( f , м²) по формулам (3)–(5) [14]. Коэффициент полезного действия рассчитывается по формуле (3)

u ■(ic -i -T■(»c -5 ))

n= —--— c--и -100%,     (3)

i p - i c - T o.c. ■ ( ⁵ p - ⁵ c )

где u – достижимый коэффициент инжекции;

• i c – энтальпия сжимаемого потока, кДж/кг;

• s с – энтропия сжимаемого потока, кДж/(кг·К);

• i и – энтальпия инжетируемого потока, кДж/кг;

• s _и – энтропия инжетируемого потока, кДж/(кг·К);

• i _р – энтальпия рабочего потока, кДж/кг;

• s _р – энтропия рабочего потока, кДж/(кг·К);

T _о.с. – температура рабочего тела в состоянии равновесия с окружающей средой, T _о.с. = 293 К [14].

Расход рабочего пара определяется по формуле (4)

G р

G c

1 + U ’

где G _c – расход сжатого пара, кг/с;

u – достижимый коэффициент инжекции.

Критическое сечение любого потока выражается формулой (5), более подробно формулы для расчета всех участков камеры смешения представлены в табл. 1 [14]:

Сравнение результатов

По результатам численного моделирования с использованием электронного симулятора эжектора, алгоритмической модели и типовых газодинамических расчетов по условиям 2, 10, 13 и 16 – инновационного и типового методов построены графики исследуемых зависимостей на рис. 5 и 6 с зависимостями P и / P р = f (η) и f 2 / f 3 = f (η) [2,7–9]. Согласно [7, 10, 14] при отношении выходного диаметра ( d c ) вых расширяющейся части сопла к диаметру ( d к ) м камеры смешения, при равном отношении ( d _c)_вых/( d _к)_м = 1,1–1,7, достигается максимальный КПД эжектора с давлением на выходе выше давления рабочего потока. Также известно, что площадь минимального поперечного сечения f ₂ конфузора камеры смешения превышает площадь минимального поперечного сечения f ₃ диффузора камеры смешения эжектора, принимаются отношение значений указанных площадей в пределах 1,1 ≤ f 2 / f 3 < 3,7 (рис. 6). По результатам теоретических и экспериментальных исследований авторов [7, 10, 14] единственным условием получения большего давления смеси «пар – жидкость» на выходе из эжектора, чем давление рабочего пара, является небольшое превышение площади f ₂ минимального поперечного сечения конфузора над площадью f ₃ минимального поперечного сечения камеры смешения, таким образом требуется выполнение условия f 2 / f 3 > 1 [7, 10, 14] .

Из табл. 2 можно сделать вывод, что отношение площадей и их варьирование позволит повысить эффективность камеры смешения эжектора, следовательно, повысить энергетическую эффективность турбинного и паротурбинного оборудования на предприятиях. С помощью электронного симулятора и соблюдения указанного соотношения диапазонов возможно выполнять расчеты быстро и без ошибок. Результаты расчетов сведены в табл. 2. Результаты моделирования камеры смешения позволяют выявить зоны эффективной работы,

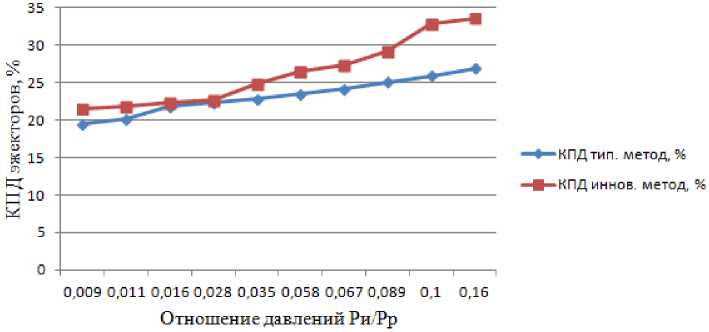
Рис. 5. Результаты многокритериального моделирования зависимости отношений давлений от КПД эжектора

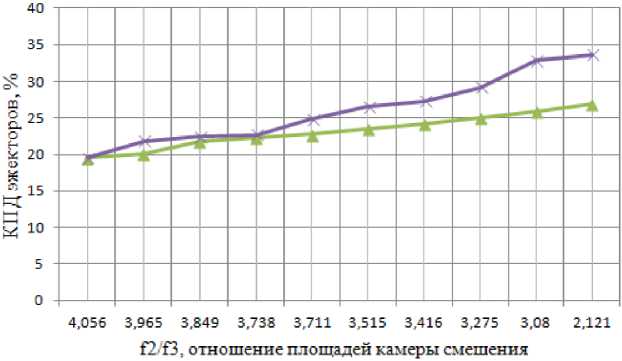
Рис. 6. Результаты стандартного (типового) и многокритериального (инновационного) моделирования с учетом отношения значений указанных площадей в пределах 1,1 ≤ f ₂ / f ₃ < 3,7

Таблица 2

Расчет оптимальных параметров пароструйных эжекторов типовым и инновационным методами

Р и / Р р , Па	КПД тип , %	КПД иннов , %	( d c)вых /( d к ) м	f 2 / f 3
1	2	3	4	5
0,009	19,5	21,5	0,667	4,056
0,011	20,1	21,8	0,750	3,965
0,016	21,8	22,4	0,800	3,849
0,028	22,3	22,7	0,933	3,738
0,035	22,8	24,8	1,067	3,711
0,058	23,5	26,5	1,200	3,515
0,067	24,2	27,3	1,333	3,416
0,089	25,1	29,2	1,467	3,275
0,1	25,9	32,8	1,600	3,080
0,16	26,9	33,6	1,789	2,121

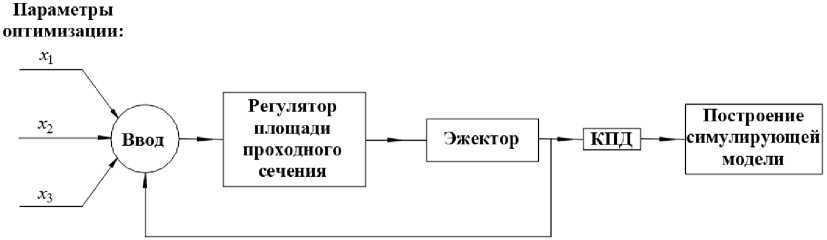
Рис. 7. Модель симулятора модели эжектора

см е ше ния, явл яе тся да вл ен ие па ров оз д у шно й с меси . У читы в а е тс я от ноше н ие п л оща дей ос е в ого конфузора и осевого диффузора ( f 2 / f 3 ).

Практическая значимость

С пом ощь ю п острое н ной а л горит ми ческой мод ел и оп т имиз ац и и п ара ме тров эж е к торов опр еде л е н ы в оз м ожнос ти бол ь ш е го пов ышени я эффективнос ти в с ра в нени и с о ст а нда рт ным и м е то да м и. И с пол ьз ов ание эл ектрон ног о с имул я тора физ ической м од ел и (ри с. 7) поз в ол ит с н из и ть в р емя проект иров а ни я и констр у и ров ан и я к ам е ры с м е ше н ия и с ред ств а на из готовл е н ие де та л ей обор удов ан ия.

Заключение

П ос та в л енная це л ь дос т иг н у та с пом ощью п острое ни я а л гори тм иче с кой м ногокри тери а л ьной мод ел и , поз в о л яюще й ос ущ е с тв и ть га з од ина м ич еские расчеты э ж е к торов с ис пол ьз ов ан ие м с ис те-

мы методов, верифицируемые с использованием электронного симулятора физической модели. Обоснованы более значительные возможности повышения эффективности пароструйного эжектора: КПД – на 7,8 % при снижении расхода пара на 3 кг/с. Многокритериальная модель использует систему методов его цифровой модели обоснования конструкции и регулирования, связанных прямыми и обратными связями. Это определило необходимость расширения состава и оптимизации системы параметров: площадь проходного сечения конструированной камеры смешения, расход пара и термодинамические параметры потоков, учитывающие давление всасывания. Результаты моделирования рекомендованы к применению в практике проектирования модернизации конструкций и эксплуатации исследуемого оборудования.