Многокритериальные системы оптимизации в агропромышленном комплексе

Оптимизацией называется целенаправленная деятельность, которая заключается в получении наилучших результатов при заданных условиях [1].

Для нахождения оптимальных решений необходимы специальные математические методы, и уже в 18 в. ученые заложили математические основы оптимизации (численные методы, вариационное исчисление и др.) [Там же]. Кроме этого, введем понятие критерия оптимальности – количественной оценки оптимизируемого качества объекта [Там же].

На основании выбранного критерия оптимальности составляют целе- вую функцию, которая представляет собой зависимость данного критерия от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации [2].

Для решения задачи оптимизации производят следующие операции:

– составление математической модели объекта оптимизации;

– выбор критерия оптимальности и составление целевой функции;

– установление возможных ограничений, которые накладываются на переменные;

– выбор метода оптимизации, позволяющего найти экстремальные значения искомых величин.

Обзор литературы

Вопросам, связанным с многокритериальной системой оптимизации, посвящено большое количество научных работ.

Например, А. Г. Трифонов уделял внимание множеству альтернативных методов; рассматривал метод достижения цели как задачу нелинейного программирования; анализировал стратегию взвешенных сумм, которая преобразует многокритериальную задачу минимизации в некую простую для всех выбранных объектов, чтобы в дальнейшем к ней можно было применить стандартный алгоритм оптимизации [3].

Учеными были предложены следующие методы многокритериальной оптимизации [4]:

– метод Ранга, предназначенный для поиска критериев на основе оценок экспертов;

– метод Preobrazovanie – для преобразования исходных данных по шкале Харрингтона;

– метод Max , представляющий собой поиск максимального значения и деление на него всех текущих значений;

– метод Ves , используемый в многомерной оптимизации (методе анализа иерархий);

– метод PoiskMaxVesa – для поиска максимального значения в методе многомерной оптимизации, позволяющий выбрать наилучшую альтернативу;

– метод Proverka , используемый в многомерной оптимизации (методе Ранга).

Д. И. Батищев, Д. Е. Шапошников рассматривали человеко-машинные процедуры решения задач многокритериального выбора. Основное внимание они уделяли анализу и использованию информации об относительной важности критериев оптимальности при принятии решений.

Исследования А. В. Лотова, И. И. Поспеловой посвящены теории много- критериальной оптимизации и методам поддержки принятия решений при нескольких критериях.

В. В. Подиновским были рассмотрены основные идеи многокритериальных систем и дано представление о методах выбора оптимальных вариантов, оцениваемых по нескольким критериям с использованием информации об их относительной важности.

Мы предлагаем применить методы многокритериальной оптимизации в сельскохозяйственном производстве.

Mатериалы и методы

Рассмотрим теплообменник, который предназначен для охлаждения горячей жидкости, в данном случае молока, от температуры t ₁ до температуры t₂. В качестве хладагента использовалась вода с температурой t ₃. Функционирование теплообменника характеризовалось следующими информационными переменными: W ₁, W ₂ – массовые расходы поступившего молока и хладагента; h – конструкционный тип теплообменника (противоточный, прямоточный пластинчатый); F – площадь поверхности теплообмена; Q – количество тепла, переданное потоком молока потоку хладагента; K – общий коэффициент теплопередачи; Δ t – среднелогарифмическая разница температур; t ₁, t ₂, t ₃, t ₄ – температуры молока и хладагента на входе и на выходе из теплообменника соответственно [5–7].

Математическую модель теплообменника представим в виде пяти информационных связей; основные уравнения теплопередачи приведем в следующих формулах [8]:

Q = K ⋅ F ⋅∆ t ,             (1)

( t 1 - t 4 ^)-( t 2 - t 3 )

In (^Д

⁽ t 2 - t 3 )

K = f ( t „ t 2 , 1 3 , 1 4 , W 1 , W 2 ) ,       (3)

^W1 • c ' ( t 1 - t 2 ) - W 2 • c 2 '( t 4 - t 3 ) = 0, (4)

Q = W i • c • ( t i - 1 2 ) .[           (5)

где с и c _в – теплоемкость молока и воды соответственно.

Перечислим оптимизирующие информационные переменные для исследуемого теплообменника: n = 5; m = 11; F = m – n = 6. Согласно технологическим условиям функционирования теплообменника, регламентированными информационными переменными в системе являются W ₁, t ₁, t ₂, t ₃.

В качестве оптимизирующих переменных были выбраны конструкционный тип теплообменника h и массовый расход хладагента W ₂. Численные значения базисных (искомых) информационных переменных ( F , Q , K , Δ t , t ₄) получим после решения математической модели теплообменника [9–11].

В качестве хладоносителя был выбран хладон R410А, который имеет следующие характеристики:

– температура кипения – -51,4 0С;

– давление насыщенного пара – 1,56 МПа;

– воспламеняемость отсутствует;

– коэффициент разрушения озона равен 0 [12–13].

Также был использован тепловой насос, для которого применялись следующие критерии оптимизации:

– коэффициенты преобразования;

– температурные показатели (на входе и выходе из насоса);

– потребляемая мощность насоса;

– производительность;

– эксплуатационные показатели [14–33].

Многокритериальная оптимизация решает множество задач параметрической и структурной оптимизации.

Для расчета параметров нагрева воды и охлаждения молока с помощью теплового насоса была использована математическая модель с учетом переменных.

Схема моделирования установки, нагрева воды и охлаждения молока представлена на рис. 1 [34].

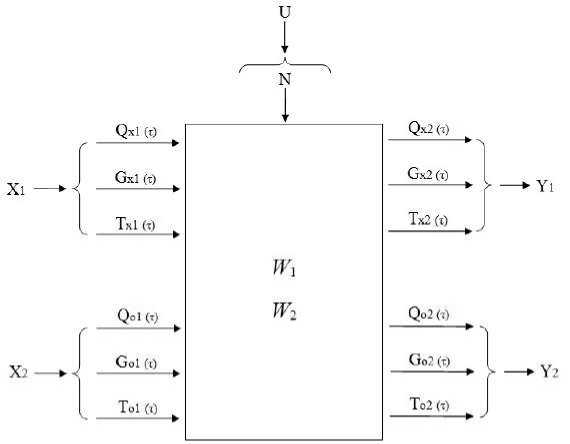
Р и с. 1. Схема моделирования установки нагрева воды и охлаждения молока

F i g. 1. Driving simulation of water heating and milk cooling installation

На данной схеме нагрев воды и охлаждение молока представлены в виде изменяющейся (динамической) системы, которая осуществляет преобразование входных воздействий в выходные переменные параметры.

Входной вектор Х1 и выходной вектор Y1 относятся к грунтовой воде:

X1 = {QX1(τ); GX1(τ); ТX1(τ)}, (6)

У1 = {QX2(τ); GX2(τ); ТX2(τ)}, (7)

где QX1(τ) – количество тепла, отбираемого грунтовой водой в единицу времени (холодопроизводительность), кВт; GX1(τ) – расход грунтовой воды на входе в насос, кг/ч; ТX1(τ) – температура грунтовой воды на входе в насос, К; QX2(τ) – количество тепла, оставшегося у грунтовой воды, кВт; GX2(τ) – расход грунтовой воды на выходе из насоса, кг/ч; ТX2(τ) – температура грунтовой воды на выходе из насоса, К.

Входной вектор Х2 и выходной вектор У2 относятся к воде, нагреваемой тепловым насосом:

X2={QO1(τ); GO1(τ); ТO1(τ)}, (8)

У2={QO2(τ); GO2(τ); ТO2(τ)}, (9)

где QO1(τ) – количество тепла, которое переносится водой, поступающей для нагревания на входе в насос, кВт; GO1(τ) – расход нагреваемой воды на входе в насос, кг/ч; ТO1(τ) – температура нагреваемой воды на входе в насос, К; QO2(τ) – количество тепла, которое передается в единицу времени нагреваемой воде, кВт; GO2(τ) – расход нагреваемой воды на выходе из насоса, кг/ч; ТO2(τ) – температура нагреваемой воды на выходе из насоса, К;

Входной управляющий вектор U является мощностью компрессора N, кВт.

Выходные векторы Y 1 и Y 2 зависят от входных векторов F₁ и F₂. Эта связь может быть выражена оператором W. При построении математической модели и ее технологического процесса необходимо установить вид и структуру оператора, который описывает зависимость выходных параметров от входных:

Y = W [X1, X2].

При нагреве воды и охлаждении молока с использованием теплового насоса мы получаем выражения:

Y1 = W1[X1; X2];

Y2 = W2[X1; X2],

У1 = {QX2(τ); GX2(τ); ТX2(τ)};

У2 = {QO2(τ); GO2(τ); ТO2(τ)}.

Входной управляющий вектор U представляет мощность компрессора N, кВт. Главная задача моделирования – получение математических зависимостей для определения холодо-QX1(t) и теплопроизводительности QO2(t) насоса:

QX1(t) = W1[N; GX1(t); ТX1(t)],

Q O2 (t) = W 2 [N; G O1 (t); Т O1 (t); Т O2 (t);

G X1 (t); Т X1 (t)].

Рассмотрим модель нагрева воды и охлаждения молока с использованием теплового насоса, которая будет являться функциональной (рис. 2) [7].

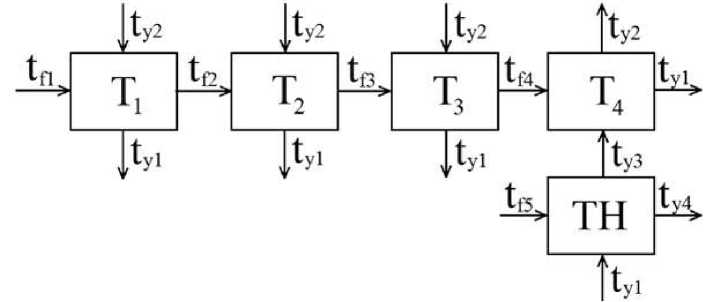
Р и с. 2. Модель нагрева воды и охлаждения молока с использованием теплового насоса F i g. 2. Model of water heating and milk cooling using a heat pump

В качестве основных уравнений при расчете теплообмена, как известно, используются уравнение теплопередачи и уравнение теплового баланса.

Определяющим фактором работы теплового насоса является, как было отмечено ранее, мощность компрессора N, поэтому необходимо установить ее зависимость от всех остальных характеристик работы теплового насоса [7]:

N = W 3 [ q x 1 ( t ) ; q 02 ( t ) ; G ( t ) ] ,

N = q ₁ – q ₂.          (10)

Коэффициент преобразования тепла вычисляется следующим образом:

K = ^{q 1} .              (11)

T N

Также укажем формулу для определения коэффициента преобразования холода:

K E = ^q _N ² .             (12)

Таким образом, тепловой насос можно считать многофункциональной системой.

Результаты исследования

Задачи однокритериальной минимизации представляют собой самую про- стую математическую модель оптимизации, в которой основная функция зависит от одной переменной. Для получения более полной характеристики параметров проектируемого объекта необходимо увеличить количество рассматриваемых критериев качества. Таким образом, задачи проектирования сложных систем всегда многокритериальны, поскольку при выборе достоверного варианта приходится учитывать множество различных требований, предъявляемых к системе.

Обсуждение и заключения

Многокритериальная оптимизация решает множество задач параметрической и структурной оптимизации. Необходимо отметить, что при использовании многокритериальной системы найти оптимальное решение гораздо сложнее, чем при однокритериальной. Однако при этом значительно повышается качество решения, а получаемые результаты достаточно приближены к реальным ситуациям поведения изучаемого объекта. Чем больше критериев качества вводится в рассмотрение, тем более точную характеристику бъекта можно получить. По нашему мнению, задачи сложных систем всегда многокритериальны, поскольку при выборе оптимального варианта необходимо учитывать множество различных требований, предъявляемых к рассматриваемому объекту.