Многомасштабный подход в задаче линейного программирования для расчета преломляющего оптического элемента, формирующего заданное распределение освещенности в дальней зоне

Задача расчета оптического элемента, формирующего заданное распределение интенсивности или освещенности, в приближении геометрической оптики представляет собой сложную теоретическую и вычислительную проблему. Она сводится к решению нелинейного дифференциального уравнения (НДУ) эллиптического типа.

При этом формулировка задачи расчета оптического элемента как решения НДУ не является удачной, поскольку предполагает гладкость поверхности оптического элемента. Данное условие ограничивает класс распределений освещенности, которые могут быть сформированы оптическим элементом. В частности, гладкая оптическая поверхность не позволяет сформировать распределение освещённости, определённое в несвязной области. А также гладкость поверхности является препятствием для формирования со сложными негладкими границами. Альтернативой являются подходы, тесно связанные с задачей перемещения масс Монжа–Канторовича. Это дает возможности для использования методов расчета соответствующих оптических элементов путем численного решения задачи перемещения масс или эквивалентных ей.

Наиболее эффективные методы расчета [1 – 11] так или иначе основаны на данной взаимосвязи. Далеко не все задачи неизображающей оптики могут быть сформулированы в виде задачи перемещения масс. В частности, такой переформулировки нет для задачи формирования заданного распределения освещенности в ближней зоне. Тем не менее некоторые идеи, связанные с задачей перемещения масс, работают и в этих случаях [12, 13]. В [9, 11] описаны известные типы оптических элементов, для которых задача расчета сводится к задаче перемещения масс с некоторой функцией стоимости.

Мы рассматриваем задачу расчета преломляющего оптического элемента, формирующего заданное распределение освещенности в дальней зоне при параллельном освещающем пучке лучей. Эта задача может быть сформулирована как задача перемещения масс Монжа–Канторовича. Но в большинстве публикаций, например, в [9, 11], рассматривается только формулировка задачи перемещения масс для задачи формирования заданного распределения интенсивности, которая эквивалентна данной. В данной статье мы явно приводим задачу перемещения масс для распределения освещенности в дальней зоне. Также мы описываем связь функционала Лагранжа и вариаци- онной задачи, которая часто фигурирует в статье о задаче перемещения масс в неизображающей оптике.

Ранее делались попытки [14, 15] использования линейной вариационной задачи для расчета отражающего элемента, формирующего заданное распределение интенсивности. Их нельзя назвать удачными, поскольку использовалось решение задачи линейного программирования, являющейся прямой аппроксимацией линейной вариационной задачи. Соответственно, из-за высокой вычислительной сложности, которую мы отмечали ранее, авторам [14, 15] удалось получить решения только для изображений, аппроксимируемых сеткой из 64 точек.

В данной статье мы демонстрируем метод, позволяющий рассчитывать оптические элементы, формирующие достаточно сложные распределения интенсивности. Мы ограничиваемся рассмотрением преломляющего оптического элемента, формирующего заданное распределение освещенности на удаленной плоскости при параллельном освещающем пучке лучей, но этот подход работает с любой задачей, допускающей переформулировку в виде задачи перемещения масс [9, 11]. Данный подход является вариантом многомасштабного метода, в определенном смысле он схож с результатами [16, 17].

Постановка задачи расчета оптического элемента

Здесь мы подробно опишем математическую формулировку задачи расчета преломляющего оптического элемента. По сравнению с реальной задачей вводятся два существенных упрощения. Во-первых, на данном этапе мы игнорируем факт наличия френелевских потерь, считая, что весь световой поток достигает экрана. При этом в дальнейшем френелевские потери можно учесть, выбрав решение, минимизирующее отклонение лучей (минимум задачи перемещения масс) и, соответственно, близкое к оптимуму по френелевским потерям. Во-вторых, рассматривается приближение «дальней зоны», то есть мы пренебрегаем размерами оптического элемента. В этом случае точка экрана, в которую попадает луч, определяется только его направлением. Это достаточно распространенное приближение в светотехнических расчетах. Например, эквивалентная задача формирования заданного распределения интенсивности рассматривается в публикациях [1, 2, 9, 11, 17]. В отличие от этих статей мы рассмотрим задачу перемещения масс непосредственно для формирования распределения освещенности в удаленной плоскости, в результате функция стоимости будет иметь несколько иной вид, чем в указанных статьях.

Пусть Е 3 - трехмерное пространство с координатами ( u 1 , u 2 , z ). Рассмотрим параллельный световой пучок, распространяющийся в направлении e = (0,0,1) и имеющий в плоскости z = 0 распределение освещённости I ( u ), u е G . На удаленной плоскости П, задаваемой уравнением z = f , расположен экран.

Предположим также, что задана преломляющая поверхность y = R ( u ), при этом показатель преломления при z< R ( x ) равен n 1 , а при z< R ( u ) равен n 2 . Она задает лучевое отображение у : G ^ П следующим образом. Луч, выходящий из точки плоскости z =0 с координатами ( u 1 , u 2 ) и направлением e , преломляясь на поверхности z = R ( u ), приобретает направление т ( u ) = ( т ₁ ( и ), т ₂ ( и ), т ₃ ( и )). Поскольку расстояние f до экрана очень велико по сравнению с размером оптического элемента, можем пренебречь размерами оптического элемента и считать, что точка пересечения преломленного луча с плоскостью z = f определяется только направлением т ( и ). Соответственно, отображение у в координатах задается формулой

* и ) = [ AW, AW у

I Т з ( и ) Т з ( и ) )

В результате на плоскости z = f формируется распределение освещённости L(x) в некоторой области D, определяемое условием сохранения светового потока jL (x) dx = J" I (и) du, (1) “ Y-1(ш)

для любого борелевского шс D .

В случае дифференцируемой поверхности рефрактора соотношение (1) можно записать в виде уравнения Монжа – Ампера:

I ( и ) = L ( у ( и )) ■ J Y ( и ), (2) где J , ( и ) - якобиан отображения у , вычисленный в точке u .

Теперь, если поверхность R неизвестна, но заданы функции I ( u ) и L ( x ) с носителями G и D соответственно, возникает задача расчета преломляющей поверхности из условия формирования заданного распределение освещенности L на удаленной плоскости z = f . То есть требуется рассчитать поверхность R , которая индуцирует биективное отображение у (описанным выше способом), для которого выполнено условие (2). Итоговая геометрия рассматриваемой нами задачи приведена на рис. 1.

Функция стоимости и задача перемещения масс

Мы будем рассматривать поверхность рефрактора как огибающую семейства плоскостей, фокусирующих в приближении дальней зоны весь световой поток в точки плоскости z = f . В дальнейшем мы будем предполагать наличие условия дальней зоны, не делая соотвестветсвующих оговорок.

Утверждение 1. Плоскость, фокусирующая весь световой поток, распространяющийся в направлении e = (0,0,1), в точку (xi, x2,f) плоскости z =f, задается уравнением вида z = £( и, x) - S, (3)

где S – константа, а n 2 xi U1 + n 2 x 2 u 2

П 1 7 X 1 ² + x 2 + f ² - n 2 f

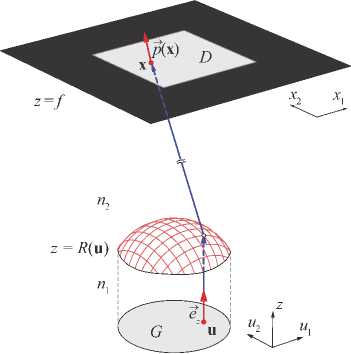
Рис. 1. Геометрия задачи

Доказательство. Предположим, преломленный луч фокусируется в точку ( x 1 , x 2 , f ). Это означает, что преломленный луч имеет направление единичного вектора

<                                       г Л

Х 1 X 2 f

^ V x 2 + x 2 + f ² V x 2 + x 2 + f ² V x 2 + x 2 + f ² _?

—*

R =

Направление входящего луча e = (0,0,1), а единичную нормаль обозначим N =( N ₁ , N ₂ , N ₃ ). Поскольку векторы N , e, R лежат в одной плоскости, можем записать

N = a ■ — + b ■ R .

Векторно умножив это соотношение на N , получим

0 = a ■ e x N + b ■ R x N ..

Поскольку векторы единичные, то e x N = sin фinc, R x N = sin фref . По закону Снелла n1 ■ e x N = n 2 ■ R x N.

Значит, a    R x N    n1

— .

b e x N n ₂

То есть N || n 1 ■^— - n ₂ ■ R , где

—      —            n 2 xi ni ■ e - n 2 ■ R = —=====,

I V x i ² + x 2 + f ²

-      n 2 x 2       n i 7 x ² + x 2 ² + f ² - n 2 f

J x i ² + x 2 + f ²       J x i ² + x 2 ² + f ²      _?

Обозначим через N _z =( N _{z 1} , N _{z 2} , N _{z 3} ) вектор, параллельный n_i ■ e - n ₂ ■ R , для которого N z 3 =i. То есть —

N z =

= n 2 x i --------. n 2 x 2 -------- 1 .

^ n_i x 2 + x 2 + f ² - n ₂ f n_i J x 2 + x 2 + f ² - n ₂ f _?

Уравнение плоскости с нормалью N z имеет вид (3). □

Поверхность z = R ( u ) является огибающей семейства поверхностей вида (3), если для некоторой дифференцируемой функции S ( x ) выполнено

R (u ) = К( u, x) - S (x), д           —

—[ ^( u , x ) - S ( x )] = 0, i =i,2. a x i

Как и в статьях [1 –5, 7, 8], мы будем рассматривать частный случай огибающих, когда во втором уравнении (5) имеет место не произвольная критическая точка, а точка минимума. В этом случае условие (5) можно записать

R ( u ) = min(K( u , x ) - S ( x )). x e D

Лучевое соответствие при этом может быть задано формулой

y ( u ) = argmin(K( u , x ) - S ( x )).

x e D

Определение 2. Отображение T : G ^ D называется интегрируемым, если для некоторой функции S e C ( D ) имеет место представление

T ( u ) = argmin(^( u , x ) - S ( x )).

x e D

Соотношение (7) полностью определяет отображение T при известной функции S . Будем обозначать такое отображение T^S .

Определение 3. Будем называть отображение T : G ^ D удовлетворяющим условию сохранения светового потока, если для любого борелевского подмножества йс D выполнено

J I ( u ) du = j L ( x ) dx .

T ^{- 1}( ш ) ^й

Условие сохранения светового потока может быть переформулировано следующим образом.

Лемма 4. Условие сохранения потока для обратимого отображения T : G ^ D равносильно любому из условий:

• i)    для любого борелевского йс D выполнено:

j I ( u ) du = J L ( x ) dx ;

T ^{- i} ( _m )               ^й

• 2)    для любой h e C ( D ) выполнено:

J h ( x ) L ( x ) dx = J h ( T ( u )) I ( u ) du ;

• 3)    I ( u ) = L ( T ( u ))^ J T ( u ), где J T ( u ) – якобиан отображения T , вычисленный в точке u .

Доказательство. Доказано в [4, lemma 4.11 ]. □

Задачу расчета оптического элемента можно сформулировать следующим образом. Для заданных распределений I(u) и L(x) требуется найти лу- чевое соответствие T: G ^ D, которое удовлетворяет условию сохранения светового потока (8) и условию интегрируемости (7), а также восстановить прямой и двойственный параметры оптического элемента.

Данная задача может быть сформулирована как задача перемещения масс Монжа-Канторовича.

Теорема 5. Рассмотрим функционал f (T) = J^(u, T(u))I(u)du ,                        (9)

G заданный на пространстве отображений T: G ^ D, удовлетворяющих условию сохранения светового потока (8). Минимум функционала f является интегрируемым отображением.

Доказательство. Скажем несколько слов о доказательстве, хотя аналогичные рассуждения приводились в [6, 8, 11]. Рассмотрим функционал Лагранжа для рассматриваемой вариационной задачи, взяв в качестве ограничений эквивалентное условие 3 из леммы 4. Возьмем произвольную це C ( G ), и пусть

И( T , ц ) = ) [К( u , T ( u )) I ( u ) + X ( T ( u )) x

G

x ( L ( T ( u )) ■ J t ( u ) - 1 ( u ))] du .

Преобразуем, пользуясь эквивалентным условием сохранения светового потока 2 из леммы 4

И( T, ц) = )[К( u, T (u)) - X( T (u))] I (u) du + r G                                          (11)

+ | X ( x ) L ( x ) dx .

D

Условный минимум функционала (9) при ограничениях (8) соответствует критической точке функционала (10). Вариация функционала И легко вычисляется. Условие 5 x И = 0, как нетрудно понять из формулы (10), равносильно условию сохранения светового потока. Условие равенства нулю вариации 5 T И = 0 равносильно условию интегрируемости (5).

Функционал Лагранжа (11) можно модифицировать таким образом, что он будет зависеть только от функции X . Заметим, что в критической точке функционала И отображение T и X связаны соотношением (7), то есть T = T ^X . Соответственно, при рассмотрении функционала мы можем заранее ограничиться парами ( T ^X , X ). Соответственно, мы можем рассматривать функционал

И( Х ) = j [K( u , T ^X ( u )) - X ( T ^X ( u ))] I ( u ) du +

, G                                             (12)

+ | X ( x ) L ( x ) dx ,

D или можно записать иначе

Нетрудно показать [11], что функционал И является вогнутым, соответственно, он может иметь только точку максимума и не более одной.

Функционал И связан с линейным функционалом Q, который мы будем рассматривать далее. Определим Q на пространстве пар функций C ( G )* C ( D ) следующей формулой

О ( ц , X ) = | ц ( u ) I ( u ) du + J X ( x ) L ( x ) dx .            (14)

GD

Заметим, что

И( X ) = Q ( ц^х , X )

для функции

Ц^X ( u ) = min[^( u , x ) -X ( x )].                     (15)

x ∈ D

Утверждение 6. Рассмотрим пару непрерывных функций ( ц , X ) е C ( G )* C ( D ). Тогда

Q ( ц , X ) <  Q ( ц^X , X ).

Доказательство. Аналогичные рассуждение приведены в доказательстве теоремы 1 в [18]. □

Кроме того, заметим, что для функции X и функции ц , определенной соотношением (15), выполнено неравенство

X( x) + ц( u) = X( x) + min[K( u, x) - X( x)] < xе D                             (16)

< X ( x ) + £( u , x ) - X ( x ) = £( u , x ).

Теперь мы можем рассмотреть линейный функционал G ( ц , X ) на пространстве пар функций с ограничениями (16):

Q = {( ц , X ) е C ( G ) x C ( D ) | ц ( u ) + X ( x ) <

< К.(u , x ) V u е G , V x е D}.

Утверждение 7. Максимумы функционалов Q и И совпадают. Если максимум И достигается в X ⁰, то максимум Q достигается в точке ( ц^X , X ⁰).

Доказательство. Из утверждения 6 следует: для каждого значения И( X ) существует равное значение G ( ц^X , X ). Наоборот, для пары ( ц , X ) eQ невозможно сопоставить значение G ( ц , X ). Тем не менее, эта пара не является экстремальной (если не имеет вид ( ц^X , X )). □

Многомасштабный подход

Мы будем рассматривать численное решение максимизации функционала

Q ( ц , X ) = | ц ( u ) I ( u ) du + j X ( x ) L ( x ) dx ^ max

G

D на пространстве

И( X ) = j min[£( u , x ) -X ( x )] I ( u ) du + J X ( x ) L ( x ) dx . (13) _Gx ∈ D                          _D

Q = {( ц , X ) е C ( G ) x C ( D ) | X ( x ) + ц ( u ) < <  K.(u , x ) V u е G , V x е D}.

Разобьем области G и D на непересекающиеся области G i и D j , соответственно,

NM

G = Цв, D = Ц D j . i=1                j=1

И пусть в каждой области G i выбраны точки u i , а в каждой D j выбрана точка X j . Функция ц ( u ) заменяется набором значений ц i в точках u i , а X ( x ) заменяется набором значений X j в точках X j . Аналогично распределения освещенности описываются наборами чисел I i и L j . Обозначим также К у = К(u , , X j ). В результате мы получим задачу линейного программирования

NM

д ( ц , X ) = ^ ц ! + YXjLj ^ max, (19) i =1             j =1

v i +k j ^ К у , i = 1, " , j = 1M .                 (20)

Дискретная задача определяется набором данных {( G i ,u i e G i )}"₁, {( D j , x j e D j )}“1. Такая дискретная схема (19), (20) используется в статьях [14, 15]. В силу огромного количество ограничений (20), даже в случае изображений небольшого размера, использовать такую дискретную схему удается лишь в очень ограниченных случаях. Скажем, в упомянутых статьях рассматривалась задача формирования изображений, имеющих размеры 5 на 5 точек. Для преодоления этой трудности можно использовать многомасштабный подход, различные варианты которого возникают и в других вариантах задачи перемещения масс, например, [16, 17]. Многомасштабный подход предполагает последовательное решение задачи на сгущающихся сетках, причем решение на более грубой сетке выступает либо начальным приближением для решения на грубой сетке, как [16, 17], либо упрощает задачу, как в рассматриваемом случае. В нашей ситуации мы используем решение на грубой сетке, чтобы избавиться от большого числа несущественных ограничений.

Предположим, что нам известны наборы чисел ( ц i ), ( X j ), являющиеся решением задачи (21), (22) для набора данных дискретизации {( G _i ^old , u _i ^old )} _i ^N ₌ ^o ₁ ^ld , {( D ^oj^ld , x ^oj^ld )} ^Mj = ^o 1 ^ld .

Заметим, что условие того, что лучевое отображение у переводит точку u в точку x , формулируется в терминах функций ц , X как

ц ( u ) + X ( x ) = К( u , x ).

Для нас будут особенно важны пары точек, которые близки к лучевой паре ( u , y ( u )) для данного приближения. Более точно, пусть выбрано некоторое число £ >0. Будем называть пару точек ( u , , x j ) квази-лучевой, если выполнено

I ^ц i + ^X j ^- K j |< ^£ .

Допустим, у нас есть более тонкая сетка new , определяемая набором данных {( G _i ^new , u _i ^new )} _i ^N ₌ ⁿ ₁ ^ew ,

{(Dnj ew, xnjew)}Mj=n1ew , которая является подразбиением сетки old. Последнее означает, что для каждого i имеется набор индексов ai,^, ani , для которых выполнено ni

Gi d = Og?  , l=1

а также для каждого j имеется набор индексов р1,., Рnj, для которых выполнено mj

D j^d = Ц D new .

l =1

Соответственно, для точки u i грубой сетки old точки u _a 1 , ., u _a ni тонкой сетки new будем называть соседями и обозначать их множество Neigh ( u i ), аналогично для x j грубой сетки old соседями будем называть точки x р_р ., x в m . тонкой сетки new и обозначать их множество Neigh ( x j ).

Если пара ( u i , x j ) сетки old является квазилучевой, пары точек тонкой сетки Neigh ( u i )× Neigh ( x j ) будем называть потенциально лучевыми. Теперь мы можем записать упрощенную задачу на тонкой сетке.

Nnew        Mnew

д(ц,X)= ^JT + YXjLT ^max,(21)

i=1

Vi+Xj< Knew(22)

для всех потенциально лучевых пар ( u i , x j ).

Заметим, что увеличение £ приводит к увеличению числа ограничений в задаче на тонкой сетке, а значит, к усложнению задачи и увеличению времени решения, соответственно, уменьшение £ приводит к упрощению задачи, тем не менее, мы получаем большие отклонения решения данной задачи линейного программирования от решения интересующей нас задачи, что в лучшем случае увеличивает число итераций, а в худшем – не дает возможности найти решение исходной задачи.

Теперь, имея последовательность измельчающихся сеток, представленных наборами данных {( G ik ) , u ik ) e G ik ) )} " i k ) , {( D j^k ) , x jk ) e D j^k ) )} M1k ) , цепочка решений зависит только от набора £ ^{( k} ) . Выбор последовательности £ ^{( k} ) имеет большое значение.

Расчетные примеры

Мы рассматриваем два расчетных примера для приведенной выше задачи на основе разработанного подхода. В качестве первого модельного примера рассмотрим расчет преломляющей поверхности, формирующей распределение освещенности в виде кольца при источнике излучения, характеризующемся плоским волновым фронтом, и равномерное распределение освещенности в виде квадрата.

В обозначениях, введенных ранее, функция освещенности источника на плоскости z =0 имеет вид

Г 1, Ы< 1,| u 2 | < 1;

I ( u ) = s

[ 0, иначе .

Расстояние до плоскости f = 1000, показатели преломления n 1 = 1,49 (полиметилметакрилат), n 2 = 1. Мы начинаем с аппроксимации требуемого распределения освещенности сеткой из 16 на 16 точек. На следующей итерации мы измельчаем обе сетки в 4 раза (вдвое равномерно уплотняем сетку по горизонтали и вертикали). Нам потребовалось три итерации, то есть в итоге изображение аппроксимируется дискретной сеткой в 64 на 64 точки. Использовались следующие значения параметров для итераций: £ (1) =10 ^- 5 , £ ⁽ 2) =10 ^- 7 . Время расчета составило несколько часов, притом что без применения многомасштабного подхода не удавалось решить задачу даже на сетке 32 на 32 точки. Все получаемые в процессе задачи линейного программирования решаются симплекс-методом. Дискретные значения, получаемые в результате решения задачи линейного программирования, аппроксимировались сплайном в программе Rhinoceros 3D. Полученный таким образом оптический элемент и результаты моделирования в программе TracePro приведены на рис. 2.

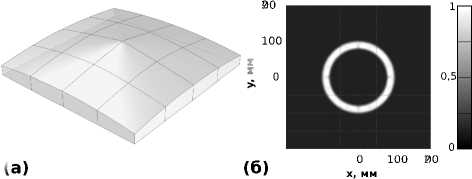
Рис. 2. Преломляющая поверхность, формирующая заданное распределение освещенности в виде кольца (а);

результат моделирования работы преломляющей поверхности в программе для светотехнических расчетов

TracePro (б)

Нормированное (на L ²-норму требуемого распределения) среднеквадратичное отклонение полученного распределения от постоянного распределения на кольце – 8,4%, световая эффективность оптического элемента – 97,2 %.

В качестве второго примера рассмотрим расчет преломляющей поверхности, формирующей распределение освещенности в виде креста при источнике освещения, характеризующемся плоским волновым фронтом, и равномерное распределение освещенности в виде круга. То есть функция освещенности источника на плоскости z =0 имеет вид i (u )=I1, || u ||" 72

[ 0, иначе .

Дискретные сетки, число итераций и пороги £ те же, что и в предыдущем примере. Рассчитанный оптический элемент и результаты моделирования в программе TracePro приведены на рис. 3.

Нормированное среднеквадратичное отклонение полученного распределения от постоянного распределения на кольце – 9,3 %, световая эффективность оптического элемента – 98,3 %.

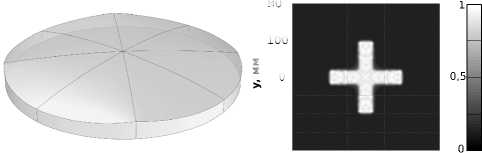
а)                          ( б)           мм

Рис. 3. Преломляющая поверхность, формирующая заданное распределение освещенности в виде креста (а); результат моделирования работы преломляющей поверхности в программе для светотехнических расчетов TracePro (б)

Заключение

В статье рассмотрен метод расчета преломляющего оптического элемента, формирующего заданное распределение освещенности на удаленной плоскости, на основе линейной вариационной задачи. Дополнительно исследована связь линейной вариационной задачи и функционала Лагранжа для задачи перемещения масс эквивалентной поставленной задачи. С помощью разработанного метода рассчитаны два оптических элемента, демонстрирующие высокие рабочие характеристики.

Работа выполнена за счет средств государственного задания в сфере научной деятельности (проект FSSS-2024-0014) в части разработки и реализации многомасштабного метода и государственного задания НИЦ «Курчатовский институт» в части установления взаимосвязи линейного функционала с функционалом стоимости.