Многомерные негармонические спектры в диагностике управляемых формирователей псевдослучайных сигналов на основе систем с динамическим хаосом
Автор: Афанасьев Вадим Владимирович, Логинов Сергей Сергеевич
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 2 т.11, 2013 года.
Бесплатный доступ
Рассматриваются многомерные негармонические спектры сигналов формирователей псевдослучайных сигналов на основе нелинейных систем с динамическим хаосом. Выполнен анализ аддитивных шумов и квазирезонансных воздействий на спектральные характеристики сигналов систем Лоренца и Чуа.
Негармонический спектральный анализ, динамический хаос, квазирезонансные воздействия
Короткий адрес: https://sciup.org/140191633
IDR: 140191633 | УДК: 519.6+621.373
Текст научной статьи Многомерные негармонические спектры в диагностике управляемых формирователей псевдослучайных сигналов на основе систем с динамическим хаосом
При формировании сигналов с воспроизводимыми статистическими характеристиками на основе нелинейных систем с динамическим хаосом актуальным является решение задачи перевода нелинейных систем с динамическим хаосом из режима с преобладанием регулярной моды в режим с преобладанием хаотический моды путем введения внешних управляющих воздействий на параметры систем. Одним из широко используемых видов управляющих воздействий на параметры нелинейных систем и параметры временной дискретизации являются квазирезонансные воздействия [1].
Нелинейные системы с динамическим хаосом характеризуются наличием как регулярных, так и хаотических мод поведения. Реальные физические системы, описываемые нелинейными дифференциальными уравнениями, находятся в условиях действия комплекса шумов и флуктуаций, которые могут существенно изменить спектрально-корреляционные и вероятностные характеристики порождаемых системами сигналов [1-2]. Применение стабилизирующих воздействий на параметры систем обеспечивают необходимую модовую структуру, которая может изменяться при действии комплекса шумов и помех в реальной помеховой обстановке. Оперативная диагностика состава текущих мод рассматриваемого класса систем, с прогнозированием его изменений во времени, позволяет прогнозировать отказы, связанные с недопустимым изменением состава текущих мод систем. Актуальной является решение задачи диагностики нелинейных систем с хаотической динамикой в условиях действия комплекса шумов и флуктуаций по порождаемым ими сигналам.
В настоящее время наиболее широко исследованы нелинейные системы с хаотической динамикой Лоренца
Х = -ст^Х-¥уД = гХ-¥-Х2;
Z = -bZ-XY;
и Чуа
X = a^Y-h(X)y, Y = X-Y + Z; (2) Z=-0Y.
Формирователи сигналов на их основе реализованы в виде специализированных интегральных радиоэлектронных схем, в которых неизбежно возникновение шумов и флуктуаций.В системах уравнений (1)-(2) X; У; Z – пространственные переменные нелинейных систем с динамическим хаосом; г;ст;Ь – параметры системы Лоренца; а ; Р "" параметры системы Чуа, //(А") – кусочно-линейная аппроксимация нелинейности системы Чуа [3]. В оперативной диагностике формирователей сигналов на основе эффектов динамического хаоса целесообразно совместное применение гармонического и негармонического обобщенного спектрального анализа формируемых сигналов [5-6]. Цель работы – диагностика управляемых квазирезонан-сными воздействиями формирователей сигналов на базе систем Лоренца и Чуа,в условиях действия комплекса аддитивных шумов,при помощи негармонического спектрального анализа сигналов.
Негармонический спектральный анализ фрактальных сигналов нелинейных радиоэлектронных систем с гармоническим спектром вида 1// проводится путем разложения временных реализаций сигналов по базису дробно-степенных функций времени, адекватного анализируемым сигналам [5-6]:
«(')-!
к
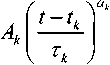
На основе представления (3) в работе получены негармонические спектры:
W^X,Y,ZV(Xw,Yw,Zw\tIT) ; W(a,r/T),
где (X,Y,ZWX0[,Y0i.Z03 – нормированные к значениям в состоянии равновесия амплитуды переменных систем Лоренца / = 1, Чуа / = 2; a – параметры дробно-степенных зависимостей; т IT – длительности дробно-степенных импульсов, нормированные к периоду квазирезонанс-ных колебаний T исследуемых систем.
Одним из широко используемых видов управляющих воздействий на параметры нелинейных систем и параметры временной дискретизации являются квазирезонансные воздействия вида [4; 7]
m(f) = m0 (1 + Mf^, (4) где m^ и mQ – мгновенное и начальное значения выбранного параметра системы; f co – функция, определяющая форму воздействий; M – коэффициент, влияющий на глубину модуляции параметра системы.
Воздействия вида (4) на параметр временной дискретизации систем позволяют стабилизировать хаотическую моду нелинейных систем с динамическим хаосом, необходимую при формировании псевдослучайных сигналов. В этом случае необходима оперативная диагностика нелинейных радиоэлектронных систем с хаотической динамикой в условиях квазирезонансных воздействий на параметры временной дискретизации.
Энергетическая эффективность управляющих воздействий зависит от их спектральных характеристик [4]. Низкочастотные (НЧ) шумы и флуктуации из области стационарных воздействий (0 Q, зависит от инерционности нелинейных систем [4]. Поэтому важной задачей является оценка влияния спектральных характеристик аддитивных шумовых воздействий на негармонические спектры сигналов нелинейных систем с хаотической динамикой.
По отношению к параметрам систем с динамическим хаосом в работе исследуются следующие шумовые воздействия на параметры систем Лоренца x = ^Y-x)+ua^x01;
Y = -XZ + rX-Y + ur (/) У01; (5) Z = XY -bZ + ub (?)20|, и Чуа
(>'-'-4))
+ Ъ1а
(0^02;
Y = X-Y + Z;
Z = -j3Y + uz^Z02,
где мЛ?); иЛ<У »/,(0 – определяют закон аддитивных воздействий по отношению к значениям ^01 ’ ^01 ’ -^01 в состоянии равновесия системы (1); »«(0; ^(^ – определяют закон аддитивных воздействий по отношению к значениям ^02 ’ ^02 ’ ^02 в состоянии равновесия системы (2).
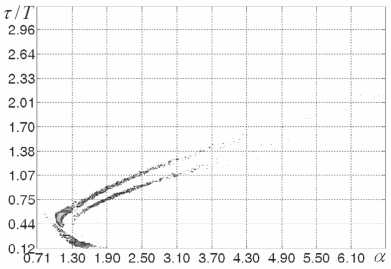
На рис. 1-2 приведены негармонические спектры сигналов X;Y системы Лоренца в условиях квазирезонансных воздействий на параметр временной дискретизации.
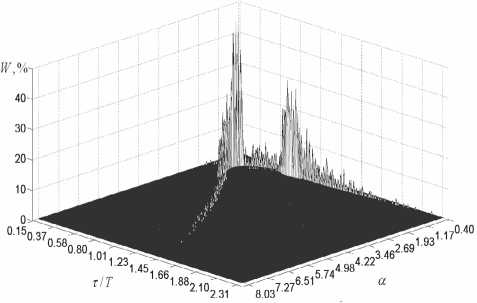
Рис. 1. Негармонический спектр сигнала системы Лоренца при воздействиях вида (4) с M = 0,2
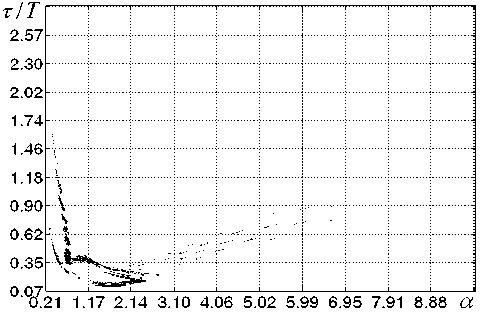
Рис. 2. Негармонический спектр сигнала системы (1) при воздействиях вида (4) с M = 0,8
На рис. 2, в отличие от рис. 1, приведено сечение негармонического спектра. Из рис. 1-2 видно, что при увеличении глубины модуляции M происходит «размывание» характерных регулярных образований в спектрах сигналов нелинейной системы Лоренца. Кроме того, в негармонических спектрах разрушаются регулярные образования, существовавшие в спектрах систем в отсутствие управляющих воздействий на параметр временной дискретизации. Это говорит о дополнительной стохастизации системы и существенном изменении структуры генерируемых ей колебаний.
С целью оценки влияния интенсивности низкочастотных шумов на характеристики сигналов системы (1) были оценены негармонические спектры при вариации интенсивностей шумов
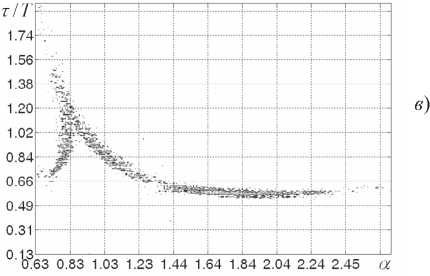
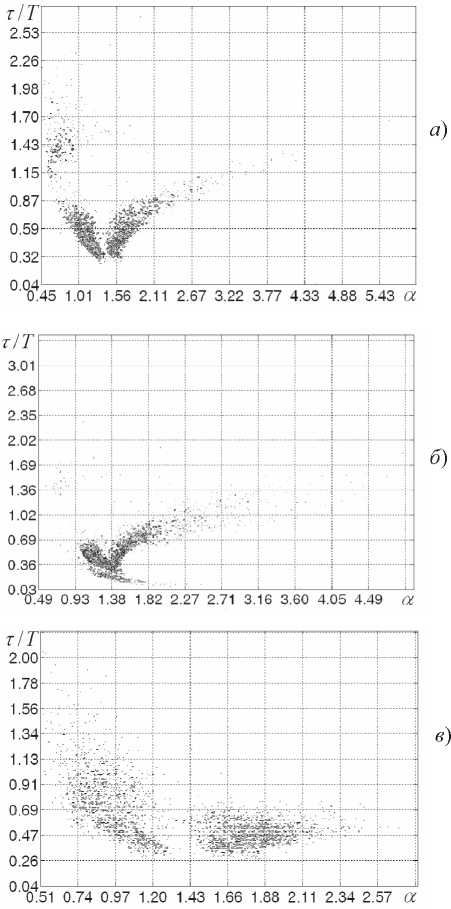
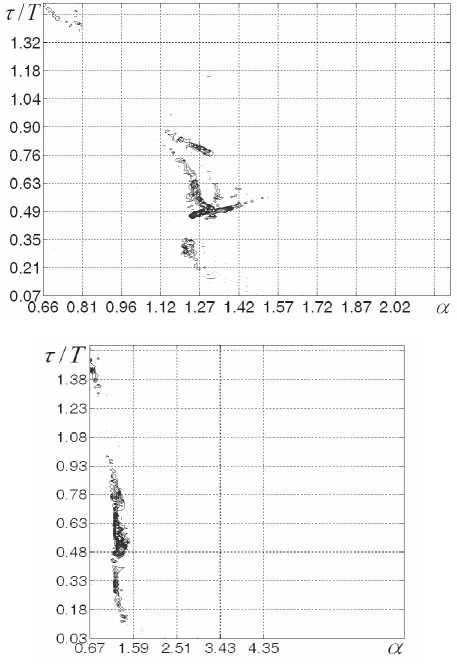
^/(^^^^/(^^^^/(^оОеЕЮ-Мо-1], где ст, – среднеквадратическое значение шума. Реализации высокочастотных шумов H^t^ с равномерным законом распределения были получены с помощью генераторов псевдослучайных чисел с использованием пакетов MathCad и MATLAB. Низкочастотные шумы формировались путем цифровой фильтрации реализаций ВЧ-шумов. Частота среза фильтров выбиралась менее частоты квазирезонансных колебаний Fc На рис. 3 приведены негармонические спектры сигналов X,Y,Z системы Лоренца в условиях аддитивных НЧ-воздействий вида (3) при фиксированном значении отношения среднеквадратического значения шумов к координатам точек равновесия систем равном (?ЛЛ)1) = МГо1) = <Ъ/(^О|) = 4-1О-3. Из рис. 3 видно, что при аддитивных шумовых воздействиях вида (3) происходит «размывание» негармонических спектров сигналов X; Y; Z. Однако, в отличие от спектров на рис. 1-2, характерные регулярные образования на спектрах рис. 3 близки по форме к образованиям, полученным в [3] при отсутствии внешних воздействий и шумов. Диапазоны изменения параметров т/Т, a практически не изменяются по сравнению с негармоническими спектрами в отсутствие шумов. Происходит лишь «расширение» спектральных линий. На рис. 4 приведены негармонические спектры сигналов X,Y,Z системы Лоренца в условиях аддитивных низкочастотных воздействий вида (3) при ^/(X0l) = o,/(y0l) = G,/(Z01) = 4.10-2. Рис. 3. Негармонические спектры сигналов системы (1) при аддитивных воздействиях вида (5) для сигналов: a) X; 6) Y ; e) Z Принципиальным отличием спектров, приведенных на рис. 4, по сравнению с рис. 3 является то, что наблюдается дальнейшее «размывание» спектральных линий и разрушение характерных спектров сигналов системы (1). На рис. 4а основная часть спектральных линий сосредоточена в пределах 0,3<г/У<0,9 и 0,7 < a<2,3 . В отличие от этого на рис. 3а спектр сосредоточен в пределах более узких линий, но в более широком диапазоне значений параметров 0,55 Рис. 4. Негармонические спектры сигналов системы Лоренца при аддитивных шумах вида (5) для сигналов: a) X; 6) Y; в) Z На рис. 5 приведены негармонические спектры сигналов X системы Чуа в условиях аддитивных низкочастотных воздействий вида (4) при фиксированном значении отношения среднеквадратического значения шумов к координатам точек равновесия системы (2) ^A^X^. В отличие от спектров сигналов системы Лоренца, приведенных на рис. 3-4, в спектрах сигнала X системы Чуа при воздействии низкочастотных шумов не происходит «размывание» спектра с сохранением характерных спектральных линий. В спектрах системы Чуа при вариации уровня шумов происходит разрушение первоначальных распределений с значительным изменением вида спектров. Аналогичные изменения происходят и со спектрами сигналов Y,Z системы Чуа. Сравнение рис. 1-2 и рис. 3-4 показывает, что спектры сигналов системы Лоренца в случае ква- зирезонансных воздействий и низкочастотных шумов имеют принципиальные различия. При квазирезонансных воздействиях происходит быстрое «разрушение» структуры первоначального спектра при увеличении глубины модуляции. В спектрах сигналов в случае низкочастотных шумов при относительно больших вариациях интенсивности воздействий сохраняется структура спектра без воздействий. a) Рис. 5. Негармонические спектры сигналов системы Чуа для аддитивных воздействиях вида (4): а) для сигнала X при а л / (А^) = 10“J; б) для сигнала У при Gj /(У02) = 4• 10 3 Выводы 1. Негармонический спектральный анализ служит эффективным средством диагностики управляемых формирователей псевдослучайных сигналов на базе систем Лоренца и Чуа. 2. Квазирезонансные воздействия на параметры временной дискретизации систем с динамическим хаосом вызывают разрушение структуры негармонических спектров сигналов систем без управляющих воздействий. 3. Аддитивные низкочастотные шумы в системе Лоренца вызывают размывание негармонических дробно-степенных спектров с сохранением их структуры, при этом степень размывания пропорциональна интенсивности шумов. В сис- 4. Анализ многомерных негармонических дробно-степенных спектров управляемых формирователей псевдослучайных сигналов позволяет определить эффективность стабилизирующих воздействий при действии комплекса шумов, и позволяет организовать оперативную диагностику состава текущих мод формирователей псевдослучайных сигналов. Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект РФФИ №10-08-00178-а).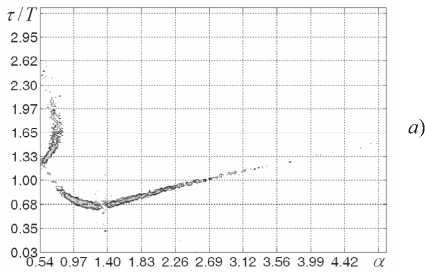
Список литературы Многомерные негармонические спектры в диагностике управляемых формирователей псевдослучайных сигналов на основе систем с динамическим хаосом
- Афанасьев В.В., Логинов С.С., Польский Ю.Е. Формирование псевдослучайных сигналов с управляемыми корреляционными характеристиками на основе систем с динамическим хаосом//ИКТ. Т.6, №2, 2008. -С. 19-22.
- Анищенко В.С., Вадивасова Т.Е., Стрелкова Г.И. Влияние шума на хаотические системы//Флуктуации и шумы в сложных системах живой и неживой природы. Казань: Изд. Минобрнауки РТ, 2008. -С. 45-91.
- Дмитриев А., Панас А. Динамический хаос. Новые носители информации для систем связи. М.: Физматлит, 2002. -252 с.
- Афанасьев В.В., Польский Ю.Е. Методы анализа, диагностики и управления поведением нелинейных устройств и систем с фрактальными процессами и хаотической динамикой. Казань: Изд. КГТУ, 2004. -219 с.
- Афанасьев В.В., Логинов С.С. Диагностика электронных динамических систем на основе негармонических дробностепенных спектров//Флуктуации и шумы в сложных системах живой и неживой природы. Казань: Изд. Минобрнауки РТ, 2008. -С. 311-334.
- Афанасьев В.В., Логинов С.С., Ценцевицкий А.А. Дробно-степенные спектры сигналов систем с хаотической динамикой//Вестник КГТУ им. А.Н. Туполева. Вып. 4(52), 2008. -С. 42-47.
- Патент РФ №2335842. Способ формирования хаотической последовательности псевдослучайных сигналов/Афанасьев В.В., Логинов С.С., Польский Ю.Е. от 13.11.2006. Опубл. 10.10.2008, бюл. №28.


