Многомодовая модель усиления света в бозе-эйнштейновском конденсате разреженных атомарных газов

Рассмотрим бозе-эйнштейновский конденсат, заключенный в магнитную ловушку с размерами порядка ЮХ 100 мкм. Как правило, в ловушке такого размера содержится 1 * 10 млн атомов. Конденсат имеет температуру около I0"9 К, что соответствует скорости движения атомов, близкой к 1 см/с. К настоящему времени удалось получить бозе-эйнштейновский конденсат ряда веществ, таких как водород, литий и пары щелочных металлов и т. д. [1; 4].

Пусть на конденсат падают два когерентных световых пучка ширины, значительно превосходящей размеры конденсата. Направления их падения перпендикулярны направлению вытянутости конденсата. Как правило, один из этих пучков более интенсивный, а другой более слабый. Первый называют одевающим («dressing», а второй — пробным («probe»). Волновые векторы этих пучков k_d и к_р образуют между собой некоторый угол (рис. 1). Частота to_d = k_d!c одевающей волны больше частоты ш_р=к_р1с пробной волны и близка к одной из частот электронного перехода в атоме. В процессе взаимодействия фотонов одевающего и пробного полей с атомом последний получает импульс отдачи. Величина этого импульса определяется значениями модулей векторов k_r к и угла между ними. Угол а и энергии фотонов h(O_d и ha) подбирают такими, чтобы разность частот была сопоставима с кинетической энергией отдачи атома V/ [5].

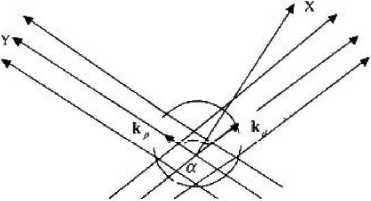
Рисунок 1

Бозе-эйнштейновский конденсат в лазерном бипучке

Сделаем ряд модельных допущений:

• 1.    Бозе-эйнштейновский конденсат рассматриваем как идеальный газ, т. е. пренебрегаем межатомным взаимодействием и учитываем лишь взаимодействие с поперечным электромагнитным полем,

• 2.    Энергию взаимодействия атома с полями светового бипучка положим много меньшей энергий разрешенных переходов в атоме.

• 3.    Число актуальных электронных состояний в атоме ограничим двумя.

• 4.    Значения полей в различных сечениях конденсата, перпендикулярных направлению его вытянутости, примем одинаковыми, т. е. не зависящими от продольной координаты.

• 5.    Атомы конденсата до взаимодействия с полями считаем покоящимися.

Волновую функции, атома с определенным значением импульса представим в виде

|^;к >=-^ехр(1кг)^ (s = a,b)

Здесь V — объем конденсата, ^(г_е,7) = = <р_л(г )ехр(-ЩИ) — волновая функция, ha)_s — энергия электронов в основном (s = о) и возбужденном (s = 6)состояниях. Отметим, что в отличие от свободного движения атома, когда импульс Йк является непрерывной величиной и может принимать любые значения, в случае ограниченного движения в ловушке его значения дискретны и их возможный набор определяется ее размерами.

Произвольное состояние атома будем описывать волновой функцией

Т= 2 с,к|як>, (2)

s=a,b;k где с — зависящие от времени коэффициенты разложения.

Электрическое поле в конденсате будем задавать суперпозицией одевающего £^и Ё пробного полей:

^E = i^ ^ ехр(-йв/) + к. с.,      (3)

каждое из которых в общем случае представляет собой набор плоских волн £ распространяющихся вблизи направления к

Е, = £ Е_(Х ехр(гкгУ к. с., (/ = d ,р)       (4)

к

Поляризацию всех волн будем считать направленной вдоль оси OZ.

Используя представление (2) и приближение вращающейся волны, можно получить уравнение Шредингера для коэффициентов с^ Оно имеет вид с,* = ?5^k' e^PHSa)t) + Я к'

-              W

+ ^Edy ] ^,k_tt- ехрНАдо) -i^c_ak,

^ ⁼ “ Т X ^[£_{р v} expd&ot) + R _ь-

+ ^£^1 ^.ц-ь ехр(-1Ддо) - 1

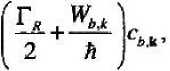
где Део = (сое - й)4) - й)^ — расстройка электронного резонанса, Зо-со^- юр, W^ — кинетическая энергия атома, обладающего импульсом в электронном состоянии ф5 (s = a,b), ГЛ—радиационная константа возбужденного электронного состояния атома, описывающая спонтанное рассеяние света в произвольных направлениях, d — матричный элемент дипольного момента перехода, черта означает комплексное сопряжение-

Поля, входящие в уравнения (5), образованы внешними полями E_dk, Ер_ки полями Е^ Е_рк, генерируемыми волнами поляризованноети среды

Р(Г,Г) = (6)

= AX Е*^’ W<>:k 14 6(г - rj | W +к.с.

Здесь N — полное число атомов в конденсате, d. — оператор электронного дипольного момента, с^_к, с£_к — коэффициенты разложения для i-того атома.

Используя волновое уравнение и считая коэффициенты разложения атомов конденсата ющихся амплитуд получим у ^ ~ ^^   + 1 ^^Л

2А„ с д?

" ^;-^ехр^¹'^Д£иг)2^с^л*к-. ^qvtr            к'

^О _Е- , Ч ^

2kd    рк ckd Bt

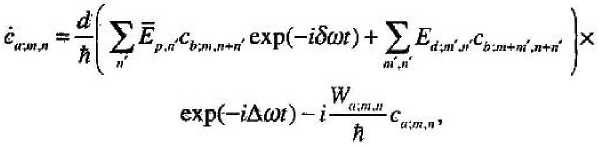
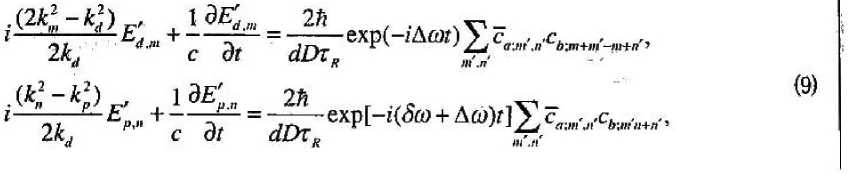
ВЕСТНИК Мордовского университета | 2007 | № S

где величина r_R = ch/7UO_dd²N_QD — сверхизлучательное время, N_o — концентрация атомов, D — поперечный размер конденсата.

Если импульс атома с состоянии |s;k> представить в форме р = йк = к\к_ш I + к_п j) = = Й(т + nj)/Z), где k_ni =-2um!D, k_n = 2nn!D и положить угол «равным 135°, пренебречь дифракцией как одевающего, так и пробного пучков, то уравнения (5), (7) можно записать в явном виде

Дополним уравнения (8), (9) начальными условиями:

с_оДО(0) = 1, с_(О) = о (_т=п*о), _(ю) Q_;m,„(0) = 0 (т,л = 0,± 1,±2,,„)

Обратим внимание на то, что решая задачу (8) — (10) и используя разложение (3), (4), мы можем найти поля лишь во внутренней области. Для нахождения полей на выходе из конденсата используем теорему Дирихле. В нашем случае

Ё/Р) = Е;ехрО^) + 25Х„,

E^D) = E^c_dexppD) + 2^E;_ra (Ц)

где E^e_p,E‘_d — амплитуды рассматриваемых полей на входе в конденсат.

Если считать размеры магнитной ловушки большими, т. е. X_}« D, пренебречь запаздыванием излучения и не учитывать зависимость полей в конденсате от координат, уравнения (8) — (10) переходят в уравнения усиления света в бозе-эйнштейновском конденсате на основе модели среднего поля, предложенной ранее [6].

Постугтяй 14.03.07.

К МНОГОМОДОВОЙ МОДЕЛИ