Многопараметрическая оптимизация конструкции лопасти несущего винта вертолета с управляемой геометрией

Автор: Аношкин А.Н., Писарев П.В., Нуреева Е.Г., Баяндин С.Р.

Журнал: Вестник Пермского национального исследовательского политехнического университета. Механика @vestnik-pnrpu-mechanics

Статья в выпуске: 3, 2024 года.

Бесплатный доступ

Во время полета лопасти несущего винта вертолета создают существенные колебания и шум в силу изменения действующих на них аэродинамических нагрузок при изменении их азимутального угла. Для снижения возникающих вибраций и шума используют различные методы. Например, с появлением активных материалов была предложена концепция несущего винта с активным закручиванием. Актуаторы, интегрированные в обшивку лопасти несущего винта, создают динамическое закручивание и искривленность лопасти, приспособленные в любой момент времени к условиям полета, существенно уменьшающие колебания и шум, а также улучшающие летные характеристики. Настоящая работа посвящена многопараметрической оптимизации конструкции лопасти несущего винта вертолета с управляемой геометрией. Сформулирована постановка задачи многопараметрической оптимизации композитной конструкции на основе термопьезоэлектрической аналогии. Выбрана целевая функция. Определены основные варьируемые параметры конструкции лопасти и сформулированы ограничения для выбранных параметров. Разработана методика проектирования конструкции лопасти с управляемой геометрией, которая включает в себя три программных блока. Первый блок - математическая модель. Второй блок - построение матрицы планирования экспериментов. Третий блок - получение поверхностного отклика и поиск экстремума. Определены оптимальные параметры активных (управляющих) и силовых элементов конструкции лопасти с управляемой геометрией. Полученное решение оптимизационной задачи сравнивалось с результатами прямого численного моделирования. При проведении прямого численного моделирования рассчитывались управляемые деформации исследуемой лопасти при различных значениях управляющего электрического напряжения, задача решалась в связанной трехмерной постановке с использованием полученных геометрических параметров. Результаты настоящего исследования могут быть применимы при проектировании конструкций с управляемой геометрией.

Еще

Многопараметрическая оптимизация, композиционные материалы, управляемая геометрия, лопасть, термопьезоэлектрическая аналогия, целевая функция, параметры оптимизации, ограничения, планирование эксперимента, методика, оптимальное проектирование

Еще

Короткий адрес: https://sciup.org/146282924

IDR: 146282924 | DOI: 10.15593/perm.mech/2024.3.01

Текст научной статьи Многопараметрическая оптимизация конструкции лопасти несущего винта вертолета с управляемой геометрией

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2024PNRPU MECHANICS BULLETIN

Во время полета лопасти несущего винта вертолета создают существенные вибрации и шум в силу изменения действующих на них аэродинамических нагрузок при изменении их азимутального угла. Это вызывает дискомфорт пассажиров, увеличение рабочей нагрузки летчика, уменьшение усталостного ресурса конструкционных элементов, ограничение скорости горизонтального полета и увеличение эксплуатационных расходов [1; 2]. Традиционный способ снижения вибраций – пассивный подход, использующий виброгасители и амортизаторы [3; 4]. Однако такой подход связан с нежелательным увеличением массы конструкции и недостаточным снижением вибраций. Позже были разработаны новые способы управления, использующие активные подходы, такие, как управление высшими гармониками (УВГ) и раздельное управление лопастями (РУЛ). Их недостатки обусловлены неблагоприятными требованиями к мощности, ограничениями на частоты возбуждения в УВГ и исключительной механической сложностью гидравлических контактных колец в РУЛ [5]. С появлением активных материалов была предложена концепция несущего винта с активным закручиванием [6-9]. Актуаторы, интегрированные в обшивку лопасти несущего винта, создают динамическое закручивание и искривленность лопасти, приспособленные в любой момент времени к условиям полета, существенно снижающие вибрации и шум, а также улучшающие летные характеристики [10–12].

В настоящее время известны некоторые работы, описывающие теоретические основы создания конструкций из полимерных композиционных материалов (ПКМ) с управляемой геометрией [13–15]. Кроме того, имеются примеры создания лабораторных экземпляров и действующих макетов таких конструкций [16–18].

Для моделирования механического поведения конструкций, оснащённых управляющими пьезоактуаторами, используют различные подходы. Например, для численного моделирования механического поведения тонкостенных композиционных пластин используют метод Релея – Ритца [19]. Однако данный метод применим только для решения плоских задач. Широкое использование в качестве эффективной методологии нашёл метод термоаналогии [20–22]. Данный метод описывает только обратный пьезоэлектрический эффект, не учитывая при этом прямой.

Кроме того, существуют модели конструкций в связанной постановке, например, модель, учитывающая эффекты инерции и жесткости материала с внедрённым пьезоэлементом, основанная на теории пластин Кирхгофа [23]. Данная модель также применима только для решения плоских задач. С помощью уравнений Лагранжа выведена связанная электромеханическая модель [24], которая учитывает только прямой пьезоэлектрический эффект. Создаются модели в связанной пьезоэлектроупругой постановке, которые верифицируются по прямому пьезоэффекту [25–27].

Настоящая работа посвящена многопараметрической оптимизации конструкции лопасти несущего винта вертолета с управляемой геометрией. Сформулирована постановка задачи на основе термопьезоэлектрической аналогии. Выбрана целевая функция. Определены основные варьируемые параметры конструкции лопасти и сформулированы ограничения для выбранных параметров. Разработана методика проектирования конструкции лопасти с управляемой геометрией. Определены оптимальные параметры активных (управляющих) и силовых элементов конструкции лопасти несущего винта вертолета с управляемой геометрией.

Постановка задачи многопараметрической оптимизации композитной конструкции

В качестве объекта настоящих исследований рассматривается трехмерная модель управляемой лопасти несущего винта вертолета с радиусом 2 м и длиной хорды 0,121 м (рис. 1). Конструкция лопасти состоит из стеклопластикового С-образного лонжерона и стеклопластиковой обшивки (со схемой армирования [+45°/-45°] с толщиной отдельного слоя 0,125 мм), пенопластового сердечника (Rifeng 52WF), балансировочного груза и пьезоактуаторов, расположенных на обшивке. Профиль лопасти соответствует аэродинамическому профилю лопасти NACA 23012.

Активное управление исследуемой лопасти обеспечивает изменение её угла закручивания. Закручивание лопасти несущего винта осуществляется с помощью набора пьезоактуаторов, интегрированных в конструкцию [7; 28–33].

В настоящее время существует несколько концепций управления вертолетными лопастями, в частности, известны концепции управления: Active Trailing Edge (ATE) [34–36], Active Twist (AT), Synergistic Smart Morphing Aileron (SSMA) [37-39]. Концепция ATE предполагает деформирование хвостовой части лопасти несущего винта. На задней кромке реализуется изгибная деформация, которая приводит к изменению геометрии. SSMA представляет собой технологию независимых механизмов управляющих поверхностей, приводимых в движение сплавом с памятью формы (SMA) и микрово-локнистыми композитными (MFC) актуаторами.

В качестве концепции управления в рамках настоящих исследований рассматривается концепция Active Twist [6; 12; 33; 40]. Отличительная особенность Active Twist заключается в том, что управляющие элементы-актуаторы могут размещаться на поверхности силовой оболочки лопасти. Таким образом, Active Twist может быть внедрена в существующие лопасти несущего винта без значительных конструктивных изменений.

Используемые в рамках технологии Active Twist крутильные пьезоактуаторы (MFC M-8557-F1) состоят из прямоугольных пьезокерамических волокон, встроенных в эпоксидную матрицу и расположенных между полиамидными пленками, к которым прикреплены параллельно расположенные электроды [41].

Направление пьезокерамических волокон в пьезоактуаторе совпадает с направлением наружных слоев обшивки для получения максимального угла кручения. Толщина пьезоактуатора составляет 0,3 мм, рабочее напряжение – от -500 до +1500 В, расстояние между электродами – 0,5 мм. Пьезоактуаторы применяются в виде активного слоя прямоугольной формы длиной 1,56 м.

Математическая модель рассматриваемой композитной конструкции лопасти с управляемой геометрией основана на постановке краевой задачи электроупругости. Для описания обратного пьезоэлектрического эффекта в рамках разработанной математической модели механического деформирования лопасти с расположенными на поверхности силовой оболочки пьезоактуаторами предложено использовать термопьезоэлектрическую аналогию между пьезоэлектрическими и термоиндуцированными деформациями. Использование данной аналогии позволяет сократить время счёта оптимизационной задачи.

Термопьезоэлектрическая аналогия основана на гипотезе об инвариантности электрического неоднородного поля в пьезоэлементе, возникающего от действия управляющего электрического напряжения на его электродах, к деформационным полям внутри объема пьезоэлемента и, как следствие, к деформированию конструкции, на поверхности которой закреплен пьезоэлемент (пьезоактуатор) [42].

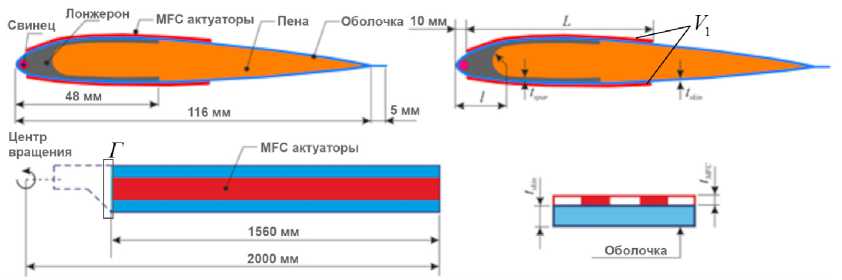
Рис. 1. Лопасть несущего винта вертолета с расчетными параметрами

Fig. 1. Helicopter main rotor blade with design parameters

Постановка краевой задачи электроупругости для исследуемой конструкции с применением термопьезоэлектрической аналогии [43] включает: уравнения равновесия (1), определяющие соотношения (2), соотношений Коши для малых упругих деформаций (3):

<5ij, j (r) = 0,(1)

° у = Cm (r )£ mn (r) -в* (r )A T,(2)

£ i(r) = [ u,j(r) + uj, i (r)]/2,(3)

где °j (r), zj (r), ui (r) - компоненты тензора напряжений, деформаций и перемещений, Cjmn (r) - компоненты тензора упругих констант, поле температурных коэффициентов в * (r ) =

e (1) nj ⁽ ^r ⁾ ^Z (1) n ⁽ ^r ),

0, r e V r g V ’

где e nij ( r ) - компоненты тензора пьезоэлектрических констант, рассчитывается через известное поле Z ( r ) с компонентами

* /Ч* * — 1

^z« n ⁽ ^r ) = E (1) n ⁽ ^r )/ ^U упр ^или См p ⁽ ^r ) = ^а (1) C (1) me (i) p_mn , ⁽⁵⁾

отождествляя величину управляющего электрического напряжения Uупр на электродах пьезоэлемента с приведенной температурой нагрева AT = Uупр , где En (r) -компоненты вектора напряженности, aj - коэффициенты линейного теплового расширения. В качестве граничных условий использовалась жесткая заделка u (r )|rеГ = °. (6)

При этом используются эффективные свойства материала актуатора [30], а коэффициенты линейного теплового расширения рассчитываются по следующей формуле:

d, a3i= (i = 1,2,3), (7)

A el где d3i - пьезоэлектрические постоянные, Ael - расстояние между пьезокерамическими волокнами в актуаторе.

Геометрическая модель представляет собой слоистую конструкцию, где каждый слой является отдельным твердым телом с заданием контактных поверхностей. При моделировании механического поведения конструкции модельной лопасти несущего винта вертолёта задавались локальные системы координат, учитывающие криволинейность поверхностей в соответствии со схемой армирования для силовой оболочки, лонжерона и пьезоактуаторов. Для ориентации конечных элементов силовой оболочки использовалась схема армирования [+45°/-45°], лонжерона – схема армирования [0°/90°], пьезоактуаторов – 45°.

В качестве граничных условий краевой задачи электроупругости для рассматриваемой конструкции модельной лопасти задавалось закрепление по границе Г, и для всего объема пьезоактуаторов (MFC) задавалась приведенная температура нагрева A Т » U упр .

Управление углом закручивания лопасти позволяет предотвратить возникновение турбулентного потока по следу лопасти, снизить шум и вибрации несущего винта вертолета. Поэтому для уменьшения вибрации лопасти в качестве целевой функции в задаче оптимизации конструкции выбрана функция угла закручивания лопасти при заданном электрическом напряжении, подаваемом на пьезоактуаторы

ф ( { X } ) ^ max, (8)

где { ^X } = { I .а,. , Г, , t skin , ^L MFC } ^- вектор проектных ^ва рьируемых параметров.

Для задачи оптимизации композитной SMART конструкции были выбраны следующие параметры: толщина и длина полок лонжерона ( t spar , l spar ), толщина силовой оболочки лопасти ( t skin ), ширина пьезоактуатора по хорде ( L MFC ).

Варьируемые при оптимизации композитной конструкции лопасти параметры представлены в табл. 1.

Таблица 1

Параметры оптимизации композитной конструкции лопасти с управляемой геометрией

Table 1

Optimization parameters of the composite blade design with controlled geometry

Конструктивные параметры	Используется для оптимизации
Ширина пьезоактуатора по хорде L MFC , мм	0 ≤ L MFC ≤ 80
Толщина оболочки t skin , мм	0,25 ≤ t skin ≤ 1,00
Толщина стенок лонжерона t spar , мм	0,50 ≤ t spar = t rib ≤ 2,00
Длина стенок лонжерона l spar , мм	34 ≤ l spar ≤ 58

В качестве конструктивных ограничений для задачи оптимизации композитной конструкции лопасти с управляемой геометрией рассматриваются местоположение центра тяжести и масса лопасти. Значения данных ограничений можно рассчитать при помощи конечно-элементной модели.

Еще одним ограничением является местоположение упругой оси лопасти. Определение местоположения упругой оси – более сложная задача, требующая решения дополнительной статической задачи кручения с двумя силами, приложенными независимо к двум сторонам отыскиваемого упругого центра (рис. 2).

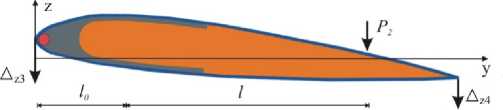
Первая сила P1 прикладывается к нефиксированной части лопасти и направлена параллельно оси z (см. рис. 2, а). Сила прикладывается на небольшом расстоянии l0 от носа лопасти. Результирующее смещение лопасти рас- считывается как Л1 = Лz 1 - Лz2. Вторая сила P2 прикладывается на расстоянии l от силы P1 (см. рис. 2, b). Результирующее перемещение лопасти рассчитывается как Л2 =Лz3 -Лz4.

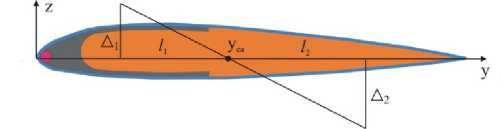
Рис. 2. Графическая презента ц ия расположения упругой оси

Fig. 2. Graphical presentation of the elastic axis

Исходя из подобия треугольников (рис. 2, c ), местоположение упругой оси находится как

yea = (10 + l1 ) = 10 +----7“.

1 +^Л 2 Л 1

Кроме того, для оптимизационной задачи были приняты следующие ограничения: толщина обшивки является дискретным значением расчетного параметра с шагом Л t ( ₊ _45/ - 45 ) = 0,25 мм; минимальная ширина пьезоактуатора по хорде начинается с 16 мм. Конструктивные ограничения для задачи оптимизации приведены в табл. 2.

Местоположение центра тяжести y cg и упругой оси y ea описываются в процентном содержании от длины хорды ( с ), ограничения для них выбраны с учетом аэро-упругой устойчивости. Ограничение для массы лопасти на единицу длины пролета выбрано из соображений желаемой динамики лопасти. Ограничения по изгибной и крутильной жесткости сформулированы в рамках конструкторских требований для исследуемой лопасти.

Таким образом, сформулирована постановка многопараметрической оптимизации композитной конструкции лопасти несущего винта вертолета с управляемой геометрией. Выбрана целевая функция. Определены параметры оптимизации конструкции лопасти. Сформулированы ограничения, используемые при решении задачи оптимизации конструкции лопасти с управляемой геометрией.

Таблица 2

Конструктивные ограничения для задачи оптимизации композитной конструкции лопасти с управляемой геометрией

Table 2

Design constraints for the optimization problem of a composite blade design with controlled geometry

Конструктивные ограничения	Границы
Местоположение центра тяжести y cg , %c	22≤ y cg ≤30
Местоположение упругой оси y ea , %c	15 ≤ y ea ≤25
Масса лопасти на единицу длины пролета m , kg/m	m ≤ 1.35
Изгибная жесткость поперек хорды EI flap , Nm²	100 ≤ EI flap ≤500
Изгибная жесткость вдоль хорды EI lag , Nm²	2600 ≤ EI lag ≤ 15400
Крутильная жесткость GJ , Nm²	64 ≤ GJ ≤ 320

Выбор параметров оптимизационной задачи для лопасти с управляемой геометрией

Для выбора значимых параметров оптимизационной задачи были проведены предварительные численные исследования влияния значений различных конструктивных параметров лопасти и пьезоактуаторов на границах диапазонов, доступных для варьирования, на угол закручивания лопасти (см. табл. 1). При исследовании влияния какого-либо параметра на значение целевой функции и конструктивных ограничений остальные параметры не изменялись. Уровень управляющего напряжения составлял 1000 В.

Анализ результатов проведенных тестовых расчетов показал, что длина стенки лонжерона оказывает наименьшее влияние на угол закручивания (4,6 %). Толщина стенки лонжерона имеет умеренный эффект (7,7 %) на угол закручивания. Наибольшее влияние на угол закручивания оказывает толщина оболочки (48 %) и длина пьезоактуатора по хорде (64 %) (рис. 3). По результатам параметрических исследований было предложено исключить параметр длины стенки лонжерона из параметров оптимизационной задачи.

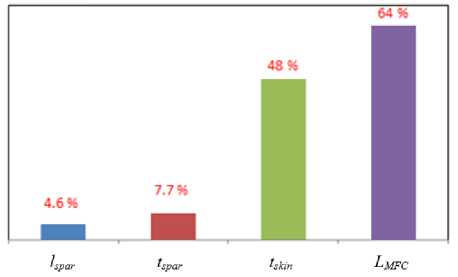
Рис. 3. Влияние параметров оптимизации на угол закручивания лопасти

Fig. 3. Influence of optimization parameters on the angle of blade twisting

В результате проведенного параметрического исследования композитной конструкции лопасти были приняты варьируемые параметры, представленные в табл. 3.

Таблица 3

Параметры оптимизации композитной конструкции лопасти с управляемой геометрией

Table 3

Optimization parameters of the composite blade design with controlled geometry

Конструктивные параметры	Используется для оптимизации
Ширина пьезоактуатора по хорде L MFC , мм	0 ≤ L MFC ≤ 80
Толщина оболочки t skin , мм	0,25 ≤ t skin ≤ 1,00
Толщина стенок лонжерона t spar , мм	0,50 ≤ t spar ≤ 2,00

Таким образом, были скорректированы параметры оптимизации конструкции лопасти несущего винта вертолета с управляемой геометрией.

Методика оптимального проектирования конструкции лопасти несущего винта вертолета с управляемой геометрией

На основе постановки и численного алгоритма решения задачи оптимизации была разработана методика оптимального проектирования конструкции лопасти несущего винта вертолета с управляемой геометрией из композиционных материалов.

Методика включает в себя три программных блока: Первый блок – математическая модель; Второй блок – построение матрицы планирования экспериментов; Третий блок – получение поверхностного отклика и поиск экстремума.

Первый программный блок обеспечивает получение численного решения задачи деформирования лопасти с использованием её математической модели с заданными значениями конструктивных параметров и системой пьезоактуаторов.

По результатам решения задачи определяется значение угла закручивания – целевой функции задачи оптимизации. Кроме того, дополнительно оцениваются жесткость лопасти, центр масс, погонная масса и первая крутильная частота лопасти с управляемой геометрией.

Второй программный блок обеспечивает построение матрицы планирования экспериментов в оптимизационной задаче, подготовку наборов исходных данных и сохранение результатов решения каждого варианта задачи деформирования лопасти с использованием первого блока, соответствующей варианту запланированного эксперимента. План экспериментов сформулирован для трех проектных параметров: а именно, tspar, tskin и LMFC и 30 экспериментальных точек. В трехмерном виде план экспериментов представлен на рис. 4. Задача нелинейной оптимизации решалась методом случайно- го поиска, используя поверхности отклика, полученные посредством вычислительной программы EdaOpt.

Третий программный блок обеспечивает построение по результатам решения задач, соответствующих плану эксперимента, целевой функции, её аппроксимации, поиск экстремума и подготовку параметров для оптимального варианта рассматриваемой конструкции лопасти. С использованием первого блока выполняется численное решение задачи о деформировании лопасти с найденными значениями параметров и заключительная проверка полученного оптимального решения.

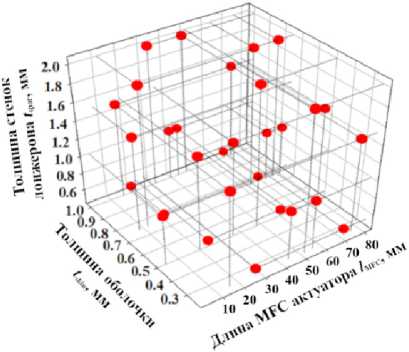
Рис. 4. Матрица планирования экспериментов в оптимизационной задаче

Fig. 4. Matrix of planning experiments in the optimization problem

Совместная работа программных блоков обеспечивается пользователем методики совместно с оператором программных комплексов. В дальнейших исследованиях планируется объединение программных блоков в единый программный комплекс с универсальным интерфейсом.

Проведение вычислительных экспериментов и определение оптимальных параметров активных (управляющих) и силовых элементов конструкции лопасти с управляемой геометрией

В качестве иллюстрации возможностей разработанной методики определялись оптимальные параметры для выбранного конструктивного варианта лопасти несущего винта вертолета с различными материалами обшивки.

Было рассмотрено два варианта конструкции лопасти с управляемой геометрией, которые отличаются материалом исполнения силовой оболочки (рис. 5): первый вариант содержит силовую оболочку из однонаправленного стеклопластика; второй вариант – текстильный стеклопластик. Материалом лонжерона в обоих случаях является однонаправленный стеклопластик.

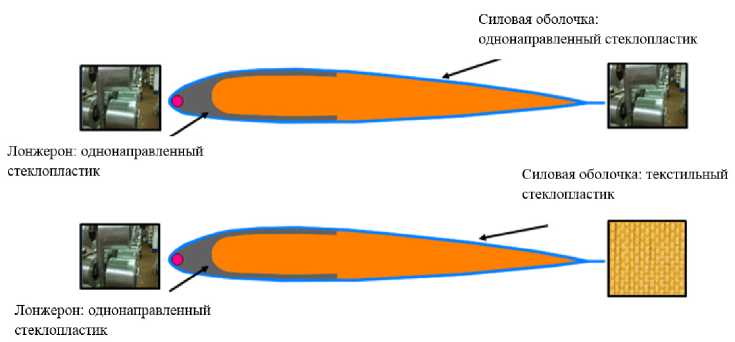
Рис. 5. Варианты SMART конструкции лопасти, которые отличаются материалом исполнения силовой оболочки

Fig. 5. Variants of the SMART blade design, which differ in the material of the power shell

Как было выявлено выше, наибольшее влияние на угол закручивания композитной конструкции лопасти с управляемой геометрией оказывает ширина пьезоактуатора по хорде L MFC. В связи с этим проводилось исследование влияния ширины актуатора по хорде на значение целевой функции и ограничений для обоих вариантов конструкции лопасти.

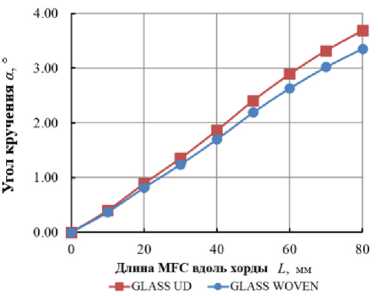
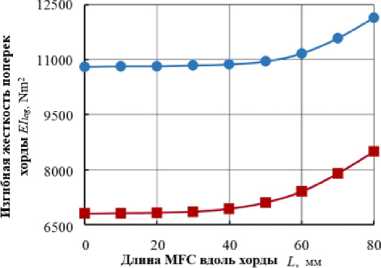
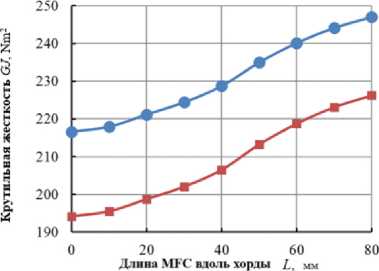
При исследовании влияния параметра ширины пьезоактуатора по хорде ( L MFC ) на значение целевой функции и конструктивных ограничений для обоих вариантов конструкции лопасти остальные параметры не изменялись ( t skin = 0,5 мм, t spar = 1,00 мм, l spar = 46,0 мм). Уровень управляющего напряжения составлял 1000 В. Используя линейность, максимальный угол кручения лопасти можно интерполировать в пределах от -500 В до 1500 В. Результаты исследования представлены на рис. 6.

Анализ графиков показал, что максимальный угол кручения достигается для варианта конструкции с оболочкой из однонаправленного стеклопластика и разница значений составляет 10,2 %. При этом более жестким является вариант конструкции с оболочкой из текстильного стеклопластика. Для всех параметров наблюдаются максимальные значения при предельной ширине пьезоактуатора. Предпочтительным является вариант с текстильной оболочкой, так как он более технологичен для подобного класса конструкций.

Результаты решения задачи многопараметрической оптимизации конструкции лопасти несущего винта вертолета с управляемой геометрией приведены в табл. 4.

В табл. 4 выделены значения конструктивных параметров, обеспечивающие максимальный угол закручивания для данных конструктивных вариантов.

Полученное решение оптимизационной задачи сравнивалось с результатами прямого численного моде- лирования методом конечных элементов. При проведении прямого численного моделирования рассчитывались управляемые деформации исследуемой лопасти при различных значениях управляющего электрического напряжения, задача решалась в связанной постановке с использованием полученных оптимальных геометрических параметров.

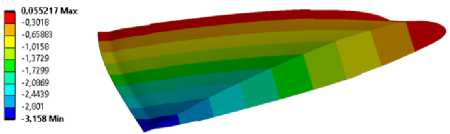
В результате численного моделирования были получены поля напряжений, деформаций и перемещений (рис. 7). По максимальным осевым перемещениям U z осуществлялся расчет угла закручивания конструкции лопасти с управляемой геометрией (10)

a = tan ¹

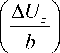
где α – угол закручивания лопасти; Δ U z – сумма перемещений носовой и хвостовой частей лопасти; b – длина хорды лопасти.

В результате численного моделирования были получены углы закручивания для первого и второго конструктивного варианта лопасти, которые составили 3,74° и 3,02° соответственно.

Результат сравнительного анализа выявил, что различие между оптимальным решением, полученным в результате поиска экстремума аппроксимационной кривой, и результатами прямого численного моделирования не превышает 9 %, что свидетельствует о хорошей корреляции полученных результатов.

Таким образом, была сформулирована методика оптимального проектирования конструкции лопасти из композиционных материалов. Проведены вычислительные эксперименты и определены оптимальные параметры активных (управляющих) и силовых элементов конструкции лопасти, выполненной из ПКМ.

Длина MFC вдоль хорды L, мм

-■-GLASS UD -«-GLASS WOVEN

■•-GLASS UD -«-GLASS WOVEN

-■-GLASS UD -«-GLASS WOVEN

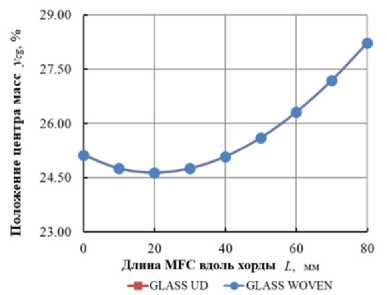
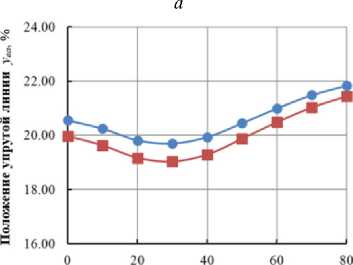
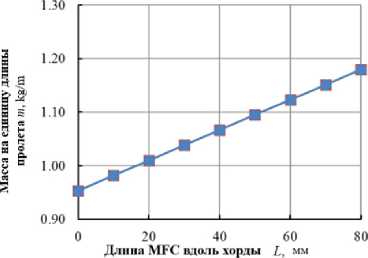
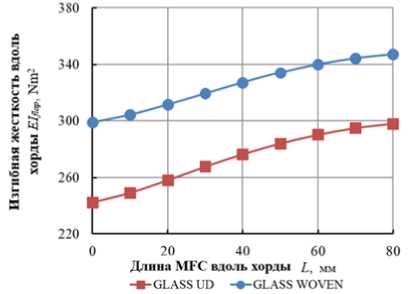
Рис. 6. Влияние ширины пьезоактуатора по хорде ( L MFC ) на: а – угол закручивания лопасти; b – расположение центра тяжести; c – расположение упругой оси; d – массу лопасти на единицу длины пролета; e – изгибную жесткость поперек хорды; f – изгибную жесткость вдоль хорды; g – крутильную жёсткость

Fig. 6. The influence of the piezoactuator width along the chord ( L MFC ) on: a – the angle of twisting of the blade; b – the location of the center of gravity; c – the location of the elastic axis; d – the mass of the blade per unit span length; e – bending stiffness across the chord; f – bending stiffness along the chord; g – torsional stiffness

Таблица 4

Результаты решения многопараметрической оптимизации конструкции лопасти с управляемой геометрией

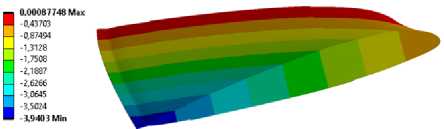
Рис. 7. Поля осевых перемещений для: а – первого конструктивного варианта лопасти; b – для второго конструктивного варианта лопасти

Table 4

The results of solving the multiparametric optimization of the blade design with controlled geometry

Первый конструктивный вариант							Второй конструктивный вариант
Конструктивные параметры							Конструктивные параметры
	min		optimal		max			min		optimal		max
l spar	34		46		58	мм	l spar	34		46		58	мм
t spar	0,5		1		2	мм	t spar	0,5		1		2	мм
t skin	0,25		0,5		1	мм	t skin	0,25		0,42		1	мм
Lmfc	0		80		80	мм	Lmfc	0		80		80	мм
Целевая функция							Целевая функция
^α 1			3,69		°		^α 1			3,31		°
Ограничения							Ограничения
y cg		22		28	30	%	y cg		22		27,7	30	%
y ea		15		21,5	25	%	y ea		15		21,8	25	%
m		0		1,18	1,35	кг/м	m		0		1,13	1,35	кг/м
EI flap		100		300	500	Нм²	EI f		100		345	500	Нм²
EI lag		2600		8500	15400	Нм²	EI l		2600		12200	15400	Нм²
GJ		64		225	320	Нм²	GI		64		247	320	Нм²

Fig. 7. Axial displacement fields for: a – the first design of the blade; b – for the second design of the blade

Заключение

В рамках настоящей работы сформулирована постановка задачи многопараметрической оптимизации конструкции лопасти несущего винта вертолета с управляемой геометрией на основе термопьезоэлектрической аналогии. Выполнен выбор варьируемых параметров для лопасти с управляемой геометрией.

Разработана методика проектирования конструкции лопасти с управляемой геометрией. Данная методика включает в себя три программных блока: математическая модель; построение матрицы планирования экспе- риментов; получение поверхностного отклика и поиск экстремума.

Список литературы Многопараметрическая оптимизация конструкции лопасти несущего винта вертолета с управляемой геометрией

Косушкин, К.Г. Анализ махового движения лопастей соосного несущего винта / К.Г. Косушкин, Б.С. Крицкий, Р.М. Миргазов // Материалы XXXIII научно-технической конференции по аэродинамике: тезисы, Жуковский, 15-16 декабря 2022 года. - Жуковский: Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского, 2022. -С. 71-72.
Вершков, В.А. Численное исследование аэродинамических характеристик шарнирного винта вертолёта в сравнении с экспериментом / В.А. Вершков, Б.С. Крицкий, Р.М. Миргазов // Материалы XXXII научно-технической конференции по аэродинамике, Жуковский, 28-29 октября 2021 года. - Жуковский: Центральный аэрогидродинамический институт им. профессора Н.Е. Жуковского, 2021. - С. 41-42.
Говердовский, В.Н. Состояние и методы повышения качества виброзащиты вертолета / В.Н. Говердовский, А.В. Зобов // Современные технологии. Системный анализ. Моделирование. - 2009. - № 4(24). - С. 191-196.
Хвощев, С.О. Проблема виброизоляции. Способы решения проблемы виброизоляции / С.О. Хвощев, Г.М. Макарьянц // Вопросы устойчивого развития общества. - 2022. -№ 8. - С. 1075-1087.
Shin, S.J. Design and simulation of integral twist control for helicopter vibration reduction / S.J. Shin, E.S. C. Cesnik, S.R. Hall // Int. J. Control Autom. Syst. - 2007 - Vol. 5, no. 1 -P. 24-34.
Bistable morphing composite structures: A review / Z. Zhang, Y. Li, X. Yu, X. Li, H. Wu, S. Jiang, G. Chai // Thin-Walled Structures. - 2019. - Vol. 142. - P. 74-97.
Electrically-latched compliant jumping mechanism based on a dielectric elastomer actuator / M. Duduta, F.C.J. Berlinger, R. Nagpal, D.R. Clarke, R.J. Wood, F. Zeynep Temel // Smart Materials and Structures. - 2019. - Vol. 28. - P. 31-38.
Power-efficient piezoelectric fatigue measurement using long-range wireless sensor networks / D. Rodenas-Herraiz, X. Xu, P. Fidler, K. Soga // Smart Materials and Structures. - 2019. -Vol. 28. - P. 1-17.
Water droplet impact energy harvesting with P(VDF-TrFE)piezoelectric cantilevers onstainless steel substrates / S.C.J. Jellard, S.H. Pu, S. Chen, K. Yao, N.M. White // Smart Materials and Structures. 2019. - Vol. 28. - P. 21-30.
Крицкий, Б.С. Исследование влияния индивидуального управления по высоким гармоникам на виброперегрузки, вызванные силой тяги несущего винта вертолета / Б.С. Крицкий, Р.М.Миргазов, В.Ч. Лэ // Научный вестник Московского государственного технического университета гражданской авиации. - 2016. - Т. 19, № 6. - С. 68-76.
Определение аэродинамических характеристик одиночной лопасти несущего винта в пакетах FLOEFD, ANSYS FLUENT И RC-VTOL / Б.С. Крицкий, М.С. Махнев, Р.М. Мир-газов, П.Н. Субботина, Т.В. Требунских // Научный вестник Московского государственного технического университета гражданской авиации. - 2016. - № 223(1). - С. 77-83.
Kessler, C. Active rotor control for helicopters: individual blade control and swashplateless rotor designs / C. Kessler // CEAS Aeronautical Journal. - 2011. - Vol. 1. - P. 23-54.
Sensitivity analysis of piezo-driven stepped cantilever beams for simultaneous viscosity and density measurement / C. Zhang, S.H. Siegel, S. Yenuganti, H. Zhang // Smart Materials and Structures. - 2019. - Vol. 28. - P. 6-72.
Deraman, A.S. Analysis of Rectangular Flexible Horizontal Piezoelectric Cantilever Beam Base on ANSYS / A.S. De-raman, R. Niirmel, M.R. Mohamad // IOP Conf. Series: Materials Science and Engineering. - 2020. - Vol. 917.
Wang, X. Optimal Control of Pretwisted Rotating Thin-Walled Beams via Piezoelectrically Induced Couplings / X. Wang, P. Xia, P. Masarati // AIAA Journal. - 2019. - Vol. 1-17.
Application of piezoelectric fiber composite actuator to aircraft wing for aerodynamic performance improvement / M. Li, J.X. Yuan, D.Guan, W.M. Chen // Science China Technological Sciences. - 2011. - Vol. 54, № 2. - Р. 395-402.
Юрлова, Н.А. Численный анализ вынужденных установившихся колебаний электровязкоупругой системы при совместном воздействии механических и электрических нагрузок / Н.А. Юрлова, Д.А. Ошмарин, Н.В. Севодина // Вестник Пермского национального исследовательского политехнического университета. Механика. - 2022. - № 4. - С. 67-79.
Matveenko, V.P. An application of graphene composites for additional damping of vibrations of smart structures based on piezoelectric elements / V.P. Matveenko, D.A. Oshmaiin, N.A. Iurlova // Advanced Structured Materials. - 2022. - Vol. 156. - P. 137-146.
Electroelastic modeling of thin-laminated composite plates with surface-bonded piezo-patches using Rayleigh-Ritz method / M.M. Gozum, A. Aghakhani, G. Serhat, I. Basdogan // Journal of Intelligent Material Systems and Structures. - 2018. -Vol. 29(10). - P. 2192-2205.
Dynamic and static modelling of piezoelectric composite structures using a thermal analogy with MSC/NASTRAN / F. Cote, P. Masson N., Mrad, V. Cotoni // Composite Structures -2004. - Vol. 65. - P. 471-484.
Dong, X.-J. Dynamic analysis of structures with piezoelectric actuators based on thermal analogy method / X.-J. Dong, G. Meng // The International Journal of Advanced Manufacturing Technology. - 2006. - Vol. 27. - P. 841-844.
Staworko, M. Modeling and simulation of piezoelectric elements - comparison of available methods and tools / M. Sta-worko, T. Uhl // Mechanics. - 2008. - Vol. 27. - P. 161-171.
Yoon, H. Kirchhoff plate theory-based electromechani-cally-coupled analytical model considering inertia and stiffness effects of a surface-bonded piezoelectric patch / H. Yoon, B.D. Youn, H.S. Kim // Smart Materials and Structures. - 2016. -Vol. 25(2), art. № 025017.
Cao, D. Modeling and power performance improvement of a piezoelectric energy harvester for low-frequency vibration environments / D. Cao, Y. Gao, W. Hu // Acta Mechanica Sinica. -2019. - Vol. - 35(4). - P. 894-911.
Kuang, Y. Evaluation and validation of equivalent properties of macro fibre composites for piezoelectric transducer modelling / Y. Kuang, M. Zhu // Composites Part B: Engineering. -2019. - Vol. 158. - P. 189-197.
Primary and secondary pyroelectric effects in macro-fiber composites / K.L. Acosta, S. Srivastava, W.K. Wilkie, D.J. Inman // Composites Part B: Engineering. - 2019. -Vol. 177. - Art. № 107275.
Baghaee, M. Modeling, analysis, and control of MFC sandwiched laminate panel flutter with general layups and arbitrary boundary conditions / M. Baghaee, A. Farrokhabadi, R.-A. Jafari-Talookolaei // Composite Structures. - 2019. -Vol. 223. - Art. № 110940.
Pan'kov, A.A. Numerical model of optical fiber piezoelectric feedback detector used for aviation composite constructions elements' geometry control / A.A. Pan'kov, P.V. Pisarev // IOP Conference Series: Materials Science and Engineering. - 2019. -Vol. 510. - Art. № 012029.
Active vibration damping of composite structures using a nonlinear fuzzy controller / H. Nasser, E.-H. Kiefer-Kamal, H. Hu, S. Belouettar, E. Barkanov // Composite Structures. - 2012. -Vol. 94. - P. 1385-1390.
Матвеенко, В.П. Использование электропроводящих композиционных материалов для дополнительного демпфирования смарт-систем на основе пьезоэлементов / В.П. Матвеенко, Д.А. Ошмарин, Н.А. Юрлова // Прикладная механика и техническая физика. - 2021. - Т. 62, № 5(369). - С. 45-57.
Bortnikov, A.D. Experimental study on active damping of compressor blade forced vibrations using piezoelements / A.D. Bortnikov // IOP Conf. Series: Materials Science and Engineering. - 2019. - Vol. 489. - Art. № 012035.
JAXA-ONERA-DLR cooperation: results from rotor optimization in hover / G. Wilke, J. Bailly, K. Kimura, Y. Tanabe // CEAS Aeronautical Journal - 2022. - Vol. 13. - P. 313-333.
Selection of the optimal airfoil for the small-sized unmanned helicopter main rotor blade / K.S. Vasil'chenko, S.V. Rez-nik, N.L. Aung, A.R. Gareev // Russian Aeronautics. - 2022. -Vol. 65, no. 3. - P. 524-532.
Structural and mechanism design of an active trailing-edge flap blade / J.H. Lee, B. Natarajan, W.J. Eun, S.R. Viswamurthy, J.-S. Park, T. Kim, S.J. Shin // Journal of Mechanical Science and Technology. - 2013. - Vol. 27. - P. 2605-2617.
Design, optimization, testing, verification, and validation of the wingtip active trailing edge / A. Wildschek, S. Storm, M. Herring, D. Drezga, V. Korian, O. Roock // Smart Intelligent Aircraft Structures (SARISTU). - 2015. - P. 219-255.
Haucke, F. Combined active separation control on the leading edge and on the trailing edge flap of a slatless high-lift configuration / F. Haucke, M. Bauer, W. Nitsche // New Results in Numerical and Experimental Fluid Mechanics X. - 2016. - P. 215-225.
Experimental investigation of an active twist model rotor blade under centrifugal loads / P. Wierach, J. Riemenschneider, S. Opitz, F. Hoffmann // Wiedemann, M. Adaptive, tolerant and efficient composite structures / M Wiedemann, M. Sinapius. - 2012. - P. 391-407.
Optimized comparative analysis of an active twist for helicopter rotor blades with C- and D-spar designs / E. Barkanov, A. Kovalov, P. Wierach, J. Riemenschneider // Mechanics of Composite Materials. - 2018. - Vol. 54. - P. 553-566.
Hoffmann, F. Structural modeling and validation of an active twist model rotor blade / F. Hoffmann, R. Keimer, J. Riemenschneider // CEAS Aeronautical Journal. - 2016. - Vol. 7. -P. 43-55.
Barkanov, E. Optimal design of the active twist for helicopter rotor blades with C-spar / E. Barkanov, S. Gluhih, A. Ko-valov // Mechanics of Advanced Materials and Structures. -2008. - Vol. 15. - P. 325-334.
SmartMaterial [Электронный ресурс]. - URL: https://www.smart-material.com/media/Datasheets/SMARTChar-geInstructionsV1%202.pdf (дата обращения: 15.06.2023).
Numerical calculation of the SMART-construction torsion angle depending on the MFC PZT fibers polarization angle / A.N. Anoshkin, P.V. Pisarev, E. Barkanov, V.A. Ashihmin // AIP Conference Proceedings. - 2019. - Vol. 2188(1). -Art. №. 040006.
Numerical calculation of composite structures equipped with flexible piezoactuators stress-strain state / A.N. Anoshkin, P.V. Pisarev, S.R. Bayandin, E.G. Kungurtseva // AIP Conference Proceedings: 28TH Russian Conference on Mathematical Modelling in Natural Sciences. - 2020. - Vol. 2216(1). -Art. №. 040013.

Еще

Статья научная