Многопорядковые дифракционные решетки с несимметричным профилем периода

МНОГОПОРЯДКОВЫЕ ДИФРАКЦИОННЫЕ РЕШЕТКИ С НЕСИММЕТРИЧНЫМ ПРОФИЛЕМ ПЕРИОДА

Среди дифракционных оптических элементов особое место занимают многопорядковые светоделительные решетки, обладающие способностью расщеплять падающий на них лазерный пучок на несколько пучков, распространяющихся под различными углами и равных по интенсивности (или с заданными соотношениями интенсивностей). С одной стороны, многопорядковые решетки не имеют аналогов среди обычных оптических элементов, а с другой - сравнительно просты для изготовления. Их периодическая структура состоит из прямолинейных штрихов различной ширины и легко поддается синтезу на стандартном фотолитографическом оборудовании, а профиль является прямоугольным и реализуется путем однократного ионного или химического травления подложки.

В свое время многопорядковые решетки были предложены и изготовлены [1, 2] как структуры с симметричным расположением штрихов в периоде относительно его середины (рис. 1а) . В этом случае наличие К штрихов в периоде обеспечивает К свободных параметров (на рис. 1а это о1-о3) , то есть величин, которые можно независимо изменять, добиваясь заданного соотношения интенсивностей в порядках дифракции. Если отказаться от ука-. занной симметрии и варьировать положения границ штрихов в левой и правой частях периода независимо друг от друга, то при том же числе штрихов К оказывается уже (2К-1) свободных параметров (рис. 16) . Из рис. 16 ясно, что положение хотя бы одной из границ штрихов, например о1 , необходимо зафиксировать.

Увеличение числа свободных параметров расширяет, естественно, возможности влияния на интенсивности света в порядках дифракции. Формально при наличии К штрихов в периоде можно обеспечить равенство (К+1) бокового порядка с каждой стороны от нулевого при симметричном периоде и 2К боковых порядков - при несимметричном. Всего с учетом нулевого порядка обеспечивается Ы=2К+3 равных порядка в первом случае и N=4K+1 - во втором. На практике далеко не всегда удается добиться максимально возможного числа равных порядков дифракции, особенно для несимметричного профиля; однако отказ от симметрии во всех случаях позволяет увеличить число равных порядков при том же количестве штрихов примерно в 1,5 раза или уменьшить количество штрихов в той же пропорции при сохранении числа равных порядков (рисунки 2, 3).

Рис. 1, Профили симметричной (а) и несимметричной (б) решеток с тремя штрихами в периоде: Т-период

Расчет интенсивностей света в порядках дифракции решетки с несимметричным профилем производится по формулам:

sln2y

= -----(C2+S?) , 1/0;

Ь п=12   1  1

Io = 1-4Q(1-Q)sina|, где

!■£ - интенсивность света в 1-ом порядке дифракции. Величины С^, Sp Q даются выражениями:

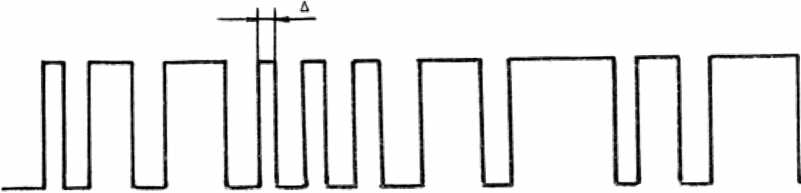
Рис. 2. Профили симметричной (а) и несимметричной (б) решеток с десятью штрихами в периоде:

a) N=23, п=65%, Д=0,011;

б) N=35, п = 75%, Д=0,020

с

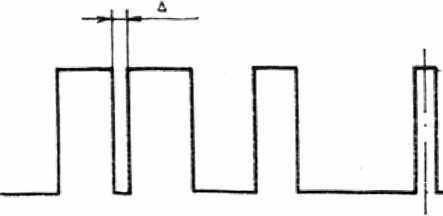
Рис. 3, Профили 17-порядковых симметричной (а) и несимметричной (б) решеток:

• а)    К=7, п=61%, Д=0,017, Ф=л;

• б)    К=5, п=7б%> Д=0,037, Ф=к

С. = 2 (-1) cos2n;lok; k=i 2К

S =  2 (-1) sin2nlak;   /(2)

• 1к=1

• ^2К к+1 Q =  2 (-1)^К+1а ;

к=1 ф - фазовая модуляция света на профиле решетки, равная Ф = Ad (п-1) ,(3)

где*

Ad - глубина профиля; п - показатель преломления материала решетки; Л - длины волны света.

Если профиль симметричный, то для всех к соблюдается условие о, - 1-0 , ,   ,(4)

к зк+i-k'

и формулы (1, 2) сводятся к известным выражениям [2]. Методика расчета решеток фактически не изменилась по сравнению с симметричным случаем [2] с тем исключением, что новая программа позволила более эффективно и целенаправленно в диалоговом режиме получать решения с необходимыми свойствами. В результате проделанных расчетов удалось прежде всего значительно увеличить максимально достигнутое общее число равных по интенсивности порядков дифракции (N =35 вместо N =23) ГПйХ               ГПЙХ

(рис. 2). Отметим, что эффективность в рабочих порядках и и ширина минимального штриха А у 35-порядковой несимметричной решетки больше, чем у 23-порядковсй симметричной.

Сводные результаты по всем полученным решениям (как симметричным, так и нет) представлены на рис. 4. Следует констатировать, что несимметричные решетки обладают значительным преимуществом в отношении такого важного при изготовлении параметра, как ширина минимального штриха в периоде. Что особенно важно, приемлемую величину этого параметра удается успешно сочетать с высокой эффективностью и глубиной профиля, соответствующей фазовой модуляции Ф=п (известно, что подобные решетки допускают наибольшие отклонения от номинальной глубины профиля при изготовлении) .

Для сравнения на рис. 3 представлены профили решеток, обеспечивающих 17 равных по интенсивности порядков дифракции. Нетрудно видеть, что несимметричное решение превосходит симметричное практически во- всех отношениях: эффективность л выше в 1,25 раза, ширина минимального штриха больше в 2,2 раза. Кроме того, расчеты показывают, что несимметричное решение допускает примерно в 2 раза больший уход размеров штрихов от номинала.

й

а

о

0,12

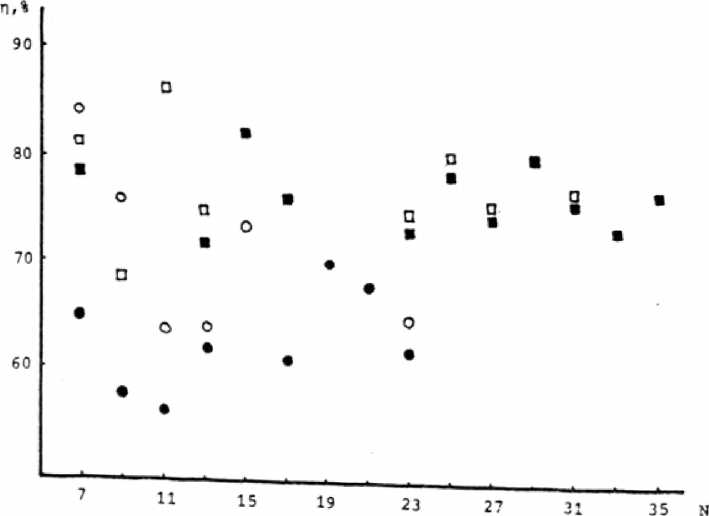
Рис. 4, Ширина минимального штриха (а) и общая эффективность в рабочих порядках (б) симметричных (о, е) и несимметричных (□,•) . решеток с различным числом равных порядков;

о, Q - решения с максимальной шириной минимального штриха;

•, ■ - решения с фазовой модуляцией ®=л

Оказывается, однако, что несимметричные решетки более чувствительны к отклонению формы профиля от прямоугольной. При изготовлении дифракционных элементов практически невозможно получить такую идеальную структуру, какая показана на рис. 1. Истинная конфигурация штрихов решетки довольно сложна и вряд ли полностью воспроизводится, но, во-видимому, с достаточной для практических целей точностью ее можно аппроксимировать трапециевидным профилем (рис. 5). Основным параметром, характеризующим этот профиль, является ширина скоса h, которая предполагается одинаковой для границ всех штрихов. Причиной появления скоса служит подтравли-вание подложки под фоторезистивной маской при химическом травлении или разрушение краев маски при ионном травлении [2], поэтому величину h называют клином травления.

Необходимо также учитывать отклонение середины скоса от расчетного положения границы штриха До (см. рис, 5). Предполагается, что эта величина постоянна по абсолютному значению для всех границ в профиле и имеет различный знак для соседних границ:

До^ = (-1)кДо,                                                        (5)

то есть реализуется согласованный уход размеров [2], характерный для фотолитографического изготовления решеток.

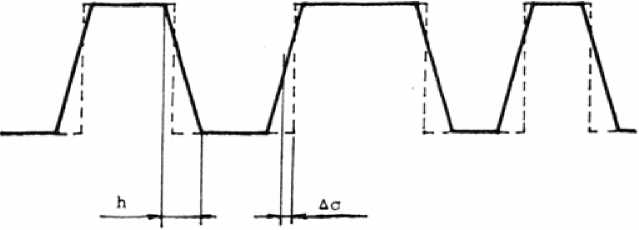
Рис* 5. Трапециевидный профиль реальной решетки (пунктиром показан идеальный расчетный профиль:

До - согласованный уход размеров; h - клин травления

Рассматривая при указанных условиях эффективность решетки в 1-ом порядке дифракции и ограничиваясь зависимостью от первых степеней До и h, поскольку это малые величины, получаем следующее приближенное выражение:

Ц = 1, +     (S.C'-C-S!) - — (С C'+S.S'),                    (6)

1    1                11           х х х х тт 1

где i^, с^, S^ даются соотношениями (1), (2), а С', S£ равны:

2К

С£ =  2 cos2nlok;

St -  2 sin2nlo

Из (6) прежде всего следует, что при согласованном уходе размеров происходит нарушение заданных соотношений интенсивностей в порядках с разными номерами, но симметрия спектра решетки, то есть равенства вида 1^=1_^, сохраняется, поскольку величина (S^С^-С^З^)/1 не зависит от знака 1. Указанный эффект имеет место как для симметричных, так и для несимметричных решеток, причем последние, как правило, более устойчивы к уходу размеров (уже отмечалось, что несимметричная 17-порядковая решетка допускает примерно в 2 раза больший уход размеров, чем симметричная) .

Наличие клина травления не приводит в первом приближении к разбросу интенсивностей в порядках с различными номерами (точнее, сохраняется равенство сумм вида 1^+^_^ ^ля различных 1), но симметрия спектра нарушается :

^гЧ = лет ‘ЧЧ+ЧЧ’-                          t3>

В случае симметричного периода, то есть при выполнении условия (4), как нетрудно убедиться, C^=S£=0, то есть асимметрия спектра не может возникнуть в принципе.

Таким образом, переход к несимметричному профилю периода приводит к необходимости более точного соблюдения прямоугольности профиля штри хов. С другой стороны, анализ распределения интенсивности света по порядкам дифракции реально изготовленной несимметричной решетки позволяет независимо от ухода размеров определить такой важный технологический параметр, как клин травления h. Для решеток с симметричным периодом это можно сделать только косвенно, предполагая непосредственную связь между клином травления и сдвигом границы штриха [2], а также зная размеры штрихов в созданной перед травлением фоторезистивной маски.

На рис. 6 представлены гистограммы спектров двух 17-порядковых решеток (показаны только рабочие боковые порядки), изготовленных в виде рельефа в стеклянной подложке, а также наиболее близкие к реальным теоретические спектры, рассчитанные по формулам (6)-(7). Оптимальнее значения До и h определялись по минимуму среднеквадратичного отклонения Д1 интенсивностей в боковых рабочих порядках теоретического спектра от реально измеренного распределения. В обоих случаях, представленных на рис. 6, величина Д1 не превышала 1,7%. Полученные результаты свидетельствуют о допустимости использования модели трапециевидного профиля при

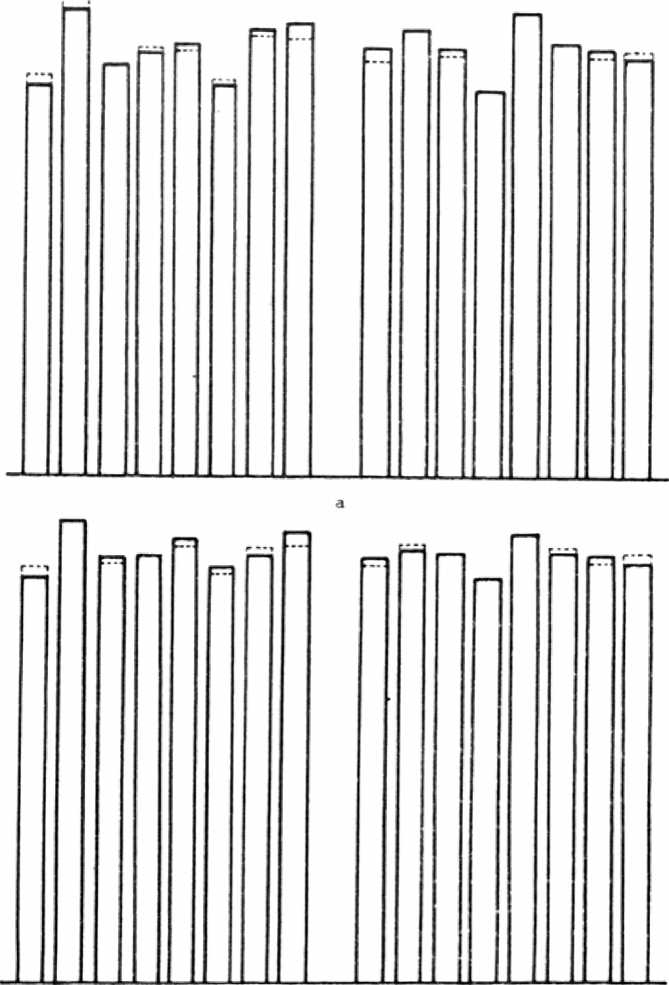
Рис. 6. Спектры реально изготовленных 17-порядковых решеток с периодом Т=159 мкм (пунктиром показаны наиболее близкие теоретические спектры):

а) До=-0,18 мкм, h=0,55 мкм, Д1=1,7%?

б) До=-0,06 мкм, h=0,40 мкм, Д1=1,4% расчете требуемых допусков на размеры и форму профиля штрихов многопорядковых решеток.