Многопорядковые комбинированные дифракционные оптические элементы для идентификации волновых аберраций различной величины

Задача измерения и коррекции аберраций волнового фронта часто встречается в оптике [1 – 3], например, в астрономических наблюдениях [4 – 7], в микроскопии [8, 9], при оптической коммуникации и кодировании [10 – 12], в офтальмологии [13 – 18] и других изображающих и фокусирующих системах [19 – 21].

Для решения этой задачи было предложено множество подходов, включая интерферометрию, теневой метод, метод Хартмана и другие [22 – 24].

Среди разработанных подходов одним из наиболее устойчивых к шумам является метод на основе Фурье-коррелятора с использованием пространственных фильтров, согласованных с базисом функций Цернике [25 – 32]. Такой датчик волнового фронта способен измерять непосредственно веса функций Цернике аберрированного волнового фронта. В частности, в работах [31, 32] была показана эффективность применения многоканальных фильтров для анализа слабых аберраций волнового фронта.

При усилении аберрации (>0,4λ) линейная аппроксимация волнового фронта становится неприем- лемой. Это объясняется тем, что вклад второго и последующих слагаемых разложения волнового фронта в ряд Тейлора становится более значительным, что приводит к детектированию ложных аберраций.

Для объективной оценки величины и типа аберрации был разработан ДОЭ [33 – 35] , согласованный с волновыми аберрациями (фазовыми функциями Цернике). Численное моделирование и экспериментальные результаты показали [34, 35] корректное детектирование волновых аберраций с величиной до длины волны λ c возможностью расширения данного диапазона.

Таким образом, для различных диапазонов величины аберраций необходимо применять разные типы согласованных фильтров.

В данной работе предлагаются многопорядковые комбинированные ДОЭ, согласованные с двумя разными типами функций (с волновыми аберрациями определенной величины и полиномами Цернике), для идентификации волновых аберраций с различным диапазоном величины. По причине того, что мы не знаем заранее величину детектируемой аберрации, предлагается рассмотреть дополнительные критерии, которые сигнализируют о наличии или отсутствии линейности волнового фронта.

Удобство такого подхода состоит в том, что регистрация изображения происходит в одной плоскости, что, в свою очередь, позволяет быстро обработать изображение (например, с применением специального алгоритма) и определить тип и вес аберрации.

В таком случае возможна сравнительная оценка преобразованных распределений по некоторым критериям, в том числе максимальному и среднему значению, а также дисперсии и относительной площади по заданному порогу.

Рассмотрим аберрированный волновой фронт, который описывается следующим уравнением

w ( r, ф ) = exp [ i v ( r , Ф )],                              (1)

где фаза может быть представлена как суперпозиция функций Цернике [36 – 38]:

y ( r, ф ) = ^ cnmZm ( r, ф ),                         (2)

. R 2n

G ( p , 0 ) =- - i - |f { i ( r , ф )

^A f 0 0

x exp

- i — r P cos( 0-ф ) A f

X

r d r d ф

где λ – длина волны, f – фокусное расстояние линзы, R – радиус оптического элемента.

• 2.    Численное моделирование действия ДОЭ

  • 2.1.    Расчёт многоканального комбинированного ДОЭ

где c _nm - весовой коэффициент аберрации, Z_nm ( r , ф ) -функции Цернике порядка ( n, m ):

На первом этапе выполнен расчёт комплексной функции пропускания комбинированного ДОЭ (6). На рис. 1 представлена амплитуда и фаза ДОЭ, рассчитанного для 49 дифракционных порядков (400×400 пикселей). Физический размер предполагаемого ДОЭ приблизительно равен 5×5 мм2 при условии размера одного пикселя 12,5×12,5 мкм2. Стоит отметить, что в настоящее время наиболее доступные технологии изготовления многоуровневых ДОЭ ограничены в разрешающей способности приблизительно 1 мкм [39, 40]. Разрешающая способность у предложенного 49-канального фильтра в 12,5 раз превышает критическую разрешающую способность,

Znm ( r , ф ) =

,

где Rn^m ( r ) – радиальные полиномы Цернике:

что говорит о сравнительно простом процессе нанесения дифракционного рисунка и возможности практического изготовления ДОЭ. В то же время предлагаемый многоканальный ДОЭ можно без проблем ре-

Rm ( r ) =

( n - m )/2

£ p=0

( - 1) ^p ( n - p )!

,f n + m   \fn-m   \ p ч ~2— p I\ ~2— p I!

,(4)

ализовать с использованием доступных как пропус-

кающих, так и отражающих пространственных модуляторов света, имеющих дискретность более 1000×700 пикселей [41, 42].

где | m | <  n , ( n - m ) - чётное.

Также известны комплексные функции Цернике с вихревой фазовой зависимостью [30]:

Znm ( r , ф ) = AnmRm ( r ) exp ( im ф ) ,

nm

4 2 n + 2, m ^ 0

V n + 1, m = 0

Для идентификации волновых аберраций различной величины предлагается использовать многопорядковый комбинированный ДОЭ с комплексной функцией пропускания:

t ( x , y ) = T 1 ( x , y ) + T ₂ ( x , y ) =

= £ exp{ i [ d qZq ( X , У ) + ( apqkX + bpqky ) ] } + ⁽⁶⁾ p , q , k

+£Zpq (x,У)exp [i(apqX + bpqy)], p,q где dpqk – весовой коэффициент закодированной волновой аберрации Zpq (r, ф), apqk, bpqk, apq, bpq - параметры пространственных несущих частот.

Поле, формируемое ДОЭ вида (6), в дальней зоне дифракции или в фокальной плоскости линзы можно описать преобразованием Фурье:

а)

б)

Рис. 1. Амплитуда (а) и фаза (б) комбинированного ДОЭ

Проведём численный расчет дифракции в фокальной плоскости ДОЭ (6) с использованием выражения (7) при следующих значениях параметров: R = 1 мм, λ =0,5 мкм, f = 100 мм. На рис. 2 представлена комбинированная картина интенсивности в фокальной плоскости. Она представляет собой 49 дифракционных порядков. В первом блоке (волновые аберрации) закодированы фазовые функции Цернике, соответствующие различным типам ( p, q ) волновых аберраций exp [ id_pqkZp_q ( x , y ) J с различными весовыми коэффициентами d pqk . Во втором блоке (полиномы Цер-нике) закодированы комплексные функции Цернике Zp_q ( x , y ) (5) с индексами (p,q ).

Стоит отметить, что второй блок дифракционных порядков согласован с функциями Цернике в экспо-

ненциальном Ẑ pq ( x , y ) представлении по причине того, что данный вид функции позволяет кодировать сразу положительные ( q >0) и отрицательные ( q <0) аберрации.

Для изготовления ДОЭ с высокой дифракционной эффективностью рассчитан фазовый ДОЭ т ( x , у ) на основе метода частичного кодирования [43, 44].

Дифракционная эффективность (8) представляет собой отношение интенсивности G(u, v) = 3 [ т ( x , у )], полученной в фокальной плоскости рассчитанного фазового ДОЭ к интенсивности G0(u, v) = 3 [ т ( x , у )], полученной в фокальной плоскости амплитуднофазового ДОЭ:

( е = G(U(и,v) dиdv ПG°(и,v) dudv

YY 1                    1 J

где Q - область интегрирования.

На рис. 3 показана фаза рассчитанного фазового ДОЭ. На рис. 4 показано распределение интенсивности (инверсия) в фокальной плоскости фазового ДОЭ. Дифракционная эффективность ε составила 60 %, а ошибка формирования картины интенсивности в фокальной плоскости ДОЭ равна 20 %.

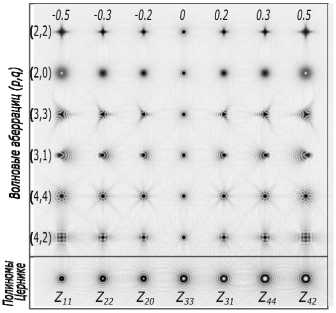
Рис. 2. Распределение интенсивности (инверсия) в фокальной плоскости ДОЭ

а)

б)

Рис. 3. Фаза (а) рассчитанного фазового комбинированного ДОЭ и масштабированный фрагмент фазы (б)

Стоит отметить, что ошибка в основном возникает за счёт шума между дифракционными порядками и искажения осесимметричных аберраций (дефокусировка, p =2, q =0).

Что касается ошибки формирования картин интенсивности в каждом дифракционном порядке, то она не превышает 10 – 13 %.

• ♦ + +**♦*

....... ^    »    *    •    ■*    *£

• •^      •)        4       »       (•       с*.®»

• 2.2. Применение комбинированного ДОЭ

■Ж      Ж      -Ж       •       :■■      ЖЖ

В    *    4     •     ••    тВ

Я  ®  ®  ®  9  О©

Рис. 4. Распределение интенсивности (инверсия) в фокальной плоскости рассчитанного фазового ДОЭ

Зададим тестовый аберрированный волновой фронт, содержащий одну волновую аберрацию:

w ( r , ф ) = exp [ i ф ( r , ф ) ] , у ( r , ф ) = CnmZnm ( r , ф ). (9)

На рис. 8 представлен результат расчёта дифракции тестового аберрированного волнового фронта w ( r , ф ) на многоканальном ДОЭ (6).

Для малых значений величины аберрации c nm волновой фронт (9) пропорционален фазе ф ( r , ф ):

exp [ i ф ( r , ф ) ] « 1 + i ф ( r , ф ) « 1 + iCnmZnm ( r , ф ) .    (1°)

В этом случае после падения волнового фронта (10) на фильтр, согласованный с комплексными функциями Цернике Zpq ( x , у ) (5), мы получим (например, для положительного m ):

g ( r , ф ) ~ [ 1 + iCnmZnm ( r , ф ) ] Zpq ( x , У ) =

= [ 1 + iCnmRm ( r ) cos( m ф ) ] Rp ( r ) exp( - iq ф ) =

= Rp ( r ) exp( - iq ф ) + °, 5iCn_mRnm ( r ) Rq ( r ) exp [ i ( m - q ) ф ] +

+ °, 5iCnmRm ( r ) Rp ( r ) exp [ - i ( m + q ) ф ] .

С учетом ортогональности угловых гармоник, в центрах всех дифракционных порядков, для которых m ^ q , будет нулевое значение. Если же m = q , то в фокальной плоскости будет поле с ненулевой интенсивностью в центре дифракционного порядка, в соответствии с преобразованием Фурье от следующей функции:

g ( r , ф ) ® Rm ( r ) exp( - im ф ) +

+ °, 5 icnmRm ( r ) Rm ( r ) [ 1 + exp( - i 2 m ф ) ] .

Анализ выражения (11) показывает, что интенсивность центрального пика будет пропорциональна квадрату модуля величины аберрации |cnm|2. Причем он будет достаточно слабым на фоне кольцевого распределения с вихревой фазой m-го порядка, соответствующего первому слагаемому в выражении (11). Однако сам факт ненулевого значения в центре тако- го дифракционного порядка можно использовать для определения диапазона величины аберрации волнового фронта.

Далее при моделировании рассмотрены волновые аберрации типа дисторсия n = 1, m = 1 (рис. 5б), астигматизм n = 2, m = 2 (рис. 5в), кома n = 3, m = 1 (рис. 5г) с весовым коэффициентом сnm ≤ 0,1λ. В таком случае СКО дифракционных порядков, отличных от полиномов Цернике (рис. 5а – г, нижний ряд дифракционных порядков), не превышает 0,10.

а)

б)

в) |G| 1.0, 0.9 0.8 0.70.6

г)

"('■ I 1 схр Ю.05/ ( V. v) |

И| > . I > схр Ю.05/ I v. v) |

(1,1)     (2,2)     (2,0)     (3,3)

IGI' '    »    *    ’

whim

(3,1)     (4,4)     (4,2) (p,q)

Lj, M £

и'(л. г) = exp /0.05Z.. (л. i l

ни

(1,1)

0.7

0.6

|G| 1.0i 0.9 0.8 0.70.6

(2,2)     (2,0)     (3,3)     (3,1)     (4,4)     (4,2)

(2,2)     (2,0)     (3,3)     (3,1)     (4,4)     (4,2) (p,q)

И<1. r) = expl (0.05Z .(.v. v)]

(1,1)

(2,2)

(2,0)     (3,3)     (3,1)     (4,4)     (4,2) (p_fq)

>   0 О Q   Q

(1,1)     (2,2)     (2,0)

>    O> >

(3,3)

и! .'. , 1 - expl (0.05Z . | .r. v)]

(3,1)     (4,4)     (4,2) lp,q)

о   О   О

д)

Рис. 5. Графики нормализованной интенсивности при анализе безаберрационного поля (а) и волнового фронта с аберрациями типа: дисторсия n = 1, m = 1 (б), астигматизм n = 2, m = 2 (в), трилистник n = 3, m = 3 (г). Детализация нормализованной интенсивности и их поперечных проекций 7-го ряда дифракционных порядков (д)

При этом картина дифракции в верхней части поля практически не меняется, однако дифракционные порядки, расположенные в нижней строке, позволяют идентифицировать вес и тип аберрации в исследуемом волновом фронте (9). На рис. 5 д представлены графики нормализованной интенсивности и проекции при x =0 только нижнего ряда дифракционных порядков.

При анализе безаберрационного волнового фронта w ( r , ϕ ) = 1 в центрах каждого дифракционного порядка регистрируется фактически нулевое распределение интенсивности.

Если задать волновой фронт с аберрацией типа дисторсия w ( r , ϕ ) = exp[ i 0,05 Z 11( x , y )], то в центре соответствующего дифракционного порядка ( p, q ) = (1,1) регистрируется ненулевое распределение интенсивности, причём значение интенсивности пропорционально связано с весовым коэффициентом c nm . В данном тестовом примере значение нормализованного весового коэффициента c 11 равно 0,37.

Зададим другой тип волновой аберрации w(r, ϕ) = exp[i0,05Z22(x, y)], тогда в центре соответствующего дифракционного порядка (p, q)=(2,2) ре- гистрируется ненулевое распределение интенсивности, равное 0,36. Рассмотрим волновую аберрацию типа трилистник w(r, ϕ) = exp[i0,05Z33(x, y)], тогда в центре соответствующего дифракционного порядка (p, q) = (3,3) регистрируется ненулевое распределение интенсивности, равное 0,39. Результаты математического моделирования согласуются с теоретическим анализом, приведенным выше.

Известно [31 – 33], что с увеличением весового коэффициента c nm исследуемой аберрации ( n, m ) более чем на 0,3 λ , дифракционные порядки, согласованные с полиномами Цернике (нижний ряд комбинированного ДОЭ), выполняют ложное детектирование, т.е. ненулевая интенсивность детектируется и в других дифракционных порядках этого ряда ( p, q ) ≠ ( n, m ). Стоит отметить, что в таком случае СКО дифракционных порядков, отличных от полиномов Цернике (рис. 5 а – г , нижний ряд), значительно возрастает.

Зададим аберрированный волновой фронт с аберрацией типа трилистник w(r, ϕ) = exp[i0,05Z33(x, y)], тогда в центре соответствующего дифракционного порядка (p, q) = (3,3), dpqk = 0,2 регистрируется корре- ляционный пик с максимальной интенсивностью в центре (рис. 6а – 3-й ряд 5-я колонка, рис. 6в).

Зададим этот же тип волновой аберрации с весовым коэффициентом с33 =0,3 w(r, ϕ) = exp[i0,05Z33(x, y)], тогда в центре соответствующего дифракционного порядка (p, q)=(3,3), dpqk = 0,3 регистрируется корреляционный пик с мак- симальной интенсивностью в центре (рис. 6б – 3-й ряд 6-я колонка, рис. 6в). Таким образом, дифракционные порядки, соответствующие волновым аберрациям (рис. 6а–б, кроме нижнего ряда, где возникают и ложные пики), позволяют идентифицировать вес и тип аберрации в исследуемом волновом фронте (9) при более высоких значениях аберраций.

в)

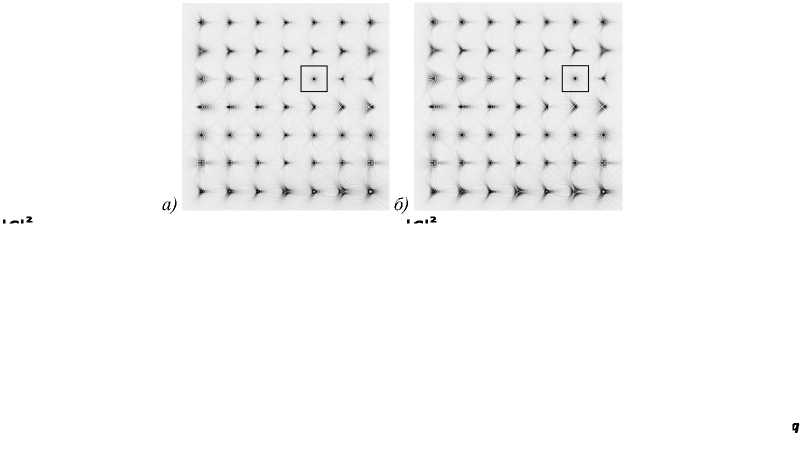
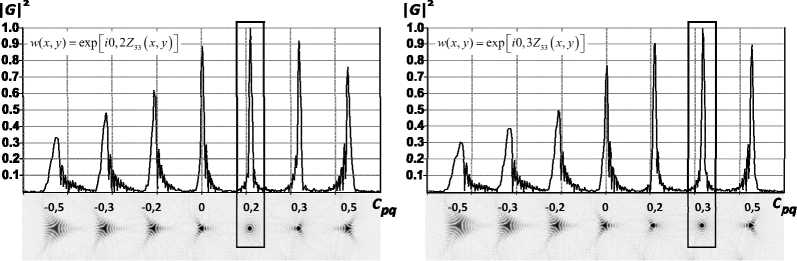
Рис. 6. Графики нормализованной интенсивности при анализе волнового фронта с аберрацией типа трилистник n = 3, m = 3 с весовым коэффициентом c 33 = 0,2 (а), c 33 = 0,3 (б). Детализация нормализованной интенсивности и их поперечных проекций 3-го ряда дифракционных порядков соответственно (в)

• 3. Автоматизация обработки фокальной картины

Хотя при численном расчете центры дифракционных порядков однозначно определяются по параметрам пространственных несущих частот в выражении (6), на практике возможно смещение этих центров, причем нелинейное. Для автоматизированного выделения на картинах фокальной интенсивности областей целевого интереса, описанных в предыдущем параграфе, был разработан специальный алгоритм. При этом отдельно рассматривается нижний ряд и вся часть поля выше этого ряда. Для анализа использованы критерии поиска максимального значения ( K 1, рамка со сплошным контуром (рис. 7, 8)), области с минимальным значением среднего ( K 2, рамка с пунктирным контуром (рис. 7, 8)), а также области с наибольшим количеством пикселов, имеющих величину выше некоторого заданного порога ( K 3, рамка с контуром в виде точек (рис. 7, 8)).

Выбор нескольких критериев связан с возможностью формирования сразу нескольких областей интереса. Например, когда вес анализируемой аберрации c nm в (9) имеет промежуточное значение между двумя закодированными в фильтре значениями (см. рис. 7). Также наличие нескольких критериев позволяет ослабить влияние возможной неравномерности площадей условных областей дифракционных порядков.

Отметим, что применение таких простых критериев для анализа нижнего ряда не подходит (см. рис. 8), так как, кроме корреляционного пика, присутствует влияние дополнительных слагаемых (см. выражение (11)).

Рис. 7. Автоматизированное определение нескольких областей интереса в ситуации, когда вес анализируемой аберрации c 20 = 0,25 (а) и c 44 = 0,25 (б) имеет промежуточное значение между двумя закодированными в фильтре значениями

б)

Рис. 8. Автоматизированное определение нескольких областей интереса в нижней строке в ситуации, когда вес анализируемой аберрации c 22 = 0,3

Таким образом, в нижней строке фокальной картины (рис. 8) оказались выделены также области, соседние с нужной. При этом добавление критерия минимальной дисперсии ( K 4, рамка с контуром в виде точки-тире (рис. 8)) не решает имеющуюся проблему.

Частотно-пространственное преобразование оптическими методами является эффективным инструментом для обработки оптических сигналов и улучшения качества изображений, в том числе для идентификации волновых аберраций в широком диапазоне величин. Существуют различные подходы, которые могут быть использованы для определения типа и веса аберрации. Выбор конкретного метода зависит от характеристики исследуемого волнового фронта, требований к точности и эффективности, а также от конкретной задачи, которую необходимо решить.

Одной из особенностей многопорядковых оптических элементов является параллельная обработка, что позволяет быстро анализировать большие объемы информации одновременно. Это особенно полезно для задач идентификации суперпозиции волновых аберраций, где требуется обработка в режиме реального времени.

В данной работе предложены и разработаны комбинированные ДОЭ, согласованные с набором волновых аберраций и полиномов Цернике. Наличие в одном ДОЭ сочетания двух разных типов согласованных функций позволяет использовать его для идентификации волновых аберраций различной величины в диапазоне от 0,05 λ до 0,5 λ .

Проведен расчёт 49-канального комбинированого ДОЭ, согласованного с волновыми аберрациями до 4го порядка (в терминах функций Цернике) и функциями Цернике. Для распознавания как малых аберраций до 0,1λ, так и более значительных искажений волнового фронта до 0,5λ установлены критерии максимального значения интенсивности, минимального значения среднего и максимального количества пикселов, имеющих величину выше некоторого заданного порога. На основе данных критериев разработан эффективный алгоритм автоматического поиска областей интереса на картинах фокальной интенсивности, что существенно упрощает процесс их анализа.

На модельных аберрированных волновых фронтах показана возможность применения разработанных оптических элементов и введённых критериев для идентификации аберраций различных диапазонов, определения их типа и количественной оценки величины искажений.

Перспективы развития предложенного метода для идентификации суперпозиции аберраций заключаются в использовании различных способов и подходов для каждого типа согласованных функций. В частности, в работе [33] показана возможность идентификации типа и веса суперпозиции слабых аберраций до

0,3λ на основе многоканального ДОЭ, согласованного с функциями Цернике. Кроме того, для идентификации суперпозиции аберрации с величиной более 0,1λ возможна поэтапная компенсация аберраций волнового фронта с применением методов оптимизации. Примерами таких подходов применительно к первому блоку дифракционных порядков (волновые аберрации) может выступать метод центральных моментов [45], алгоритм Левенберга–Марквардта [46] и др. В работах [35, 47] представлен итерационный алгоритм коррекции волнового фронта на основе оптического разложения по волновым аберрациям, где на каждой итерации выполняется компенсация аберраций волнового фронта с учетом коэффициентов разложения.

Таким образом, представленный метод позволяет значительно расширить диапазон величин детектируемых аберраций при помощи одного комбинированного ДОЭ, что имеет важное значение для решения фазовой проблемы.

Исследование выполнено за счет гранта Российского научного фонда № 24-79-10101, (в части численного моделирования), а также в рамках Государственного задания НИЦ «Курчатовский институт» (в теоретической части).