Многослойные ортогональные структуры на основе последовательностей максимальной длины

Последовательности максимальной длины (MLS – Maximum Length Sequences) как объект исследования в данной работе выбраны не случайно. На протяжении многих лет они были и остаются основным средством имитации сигналов с равномерным распределением энергии по спектру [1–3]. Их способы генерации тривиальны, не требуют особых затрат ресурсов, а также не вносят существенных задержек в работу систем, которые их используют.

Области применения MLS обширны, достаточно выделить наиболее популярные:

• •    расширение спектра сигнала;

• •    синхронизация;

• •    скремблирование.

В каждом из них MLS занимают особое место. Так, например, расширение спектра прямыми последовательностями (DSSS – Direct Sequence Spread Spectrum) [4–9], которому в данной статье уделено значительное внимание, с увеличением базы сигнала обеспечивает улучшение его энергетических характеристик и существенно повышает помехоустойчивость.

В зависимости от той или иной технологии передачи данных расширение спектра методом DSSS может быть реализовано при помощи последовательностей Баркера, Уолша [10], а также упомянутых выше MLS или построенных на их основе кодов Касами и Голда [11; 12]. Принцип расширения спектра прямыми последователь- ностями на сегодняшний день заложен в основу таких технологий, как Wi-Fi, CDMA, GPS, ГЛОНАСС и других.

Необходимо отметить, что технология расширения спектра сигнала методом DSSS идет рука об руку с кодовым разделением каналов (CDMA – Code Division Multiple Access) [10; 13; 14]. Данный способ множественного доступа основывается на применении специальных кодовых конструкций, которые не связаны с частотными и временными диапазонами и, следовательно, могут передаваться в общей полосе частот и в один промежуток времени. Таким образом, основным условием при построении системы CDMA является выбор кодовых комбинаций, которые вместе с увеличением базы сигналов исключили бы их влияние друг на друга в процессе передачи информации в общем спектре.

Примеры, приведенные в работе [14], наглядно демонстрируют возможности применения MLS в задачах CDMA. Очевидно, что дальнейшие исследования в этой области являются чрезвычайно актуальными. Особый интерес представляет анализ возможности контроля за передачей сигнала, полученного в результате кодового уплотнения при помощи рекуррентных последовательностей. Во-первых, важной особенностью MLS является высокая помехоустойчивость, которая позволяет использовать данные кодовые конструкции в условиях значительного уровня помех. Во-вторых, необходимо упомянуть о существовании математической модели системы, которая использует

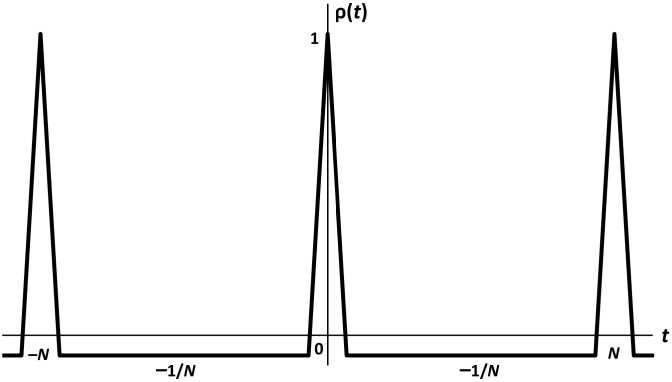
Рисунок 1. АКФ для MLS с полным периодом

в качестве комбинации цикловой фазы рекуррентную последовательность максимальной длины с заданной начальной фазой [15].

Задача синхронизации, подробно описанная в статье [16], является актуальной как для синхронной, так и для асинхронной системы передачи данных. Предлагаемый в работе [16] метод синхронизации на основе MLS позволяет достаточно эффективно противостоять фазовым сбоям, обеспечивает защиту от ошибок и даже способен обнаруживать начало блока данных еще до полной обработки комбинации цикловой фазы. Используемые при этом методы декодирования MLS опираются на специальный математический аппарат линейной алгебры – двойственный базис поля Галуа. Настоящая работа ставит перед собой целью найти способы его применения для обработки уплотненного сигнала, который был сформирован при помощи кодовых конструкций на основе последовательностей максимальной длины.

Использование MLS в CDMA

В научной литературе часто встречаются синонимы, которые, несмотря на свое широкое понятие, чаще всего используются для определения MLS:

• •    М-последовательность;

• •    Эквидистантный, код максимальной длины;

• •    ПСП, ШПС, PRN (псевдослучайная последовательность, шумоподобный сигнал, псевдослучайный шумовой код).

Последовательности максимальной длины относятся к классу псевдослучайных последовательностей [3]. Вместе с этим они представляют собой кодовые комбинации циклического (n, к) кода с максимально возможным кодовым расстоянием, что обеспечивает их высокую поме- хоустойчивость [3]. Классические MLS, которые были построены на основе одного многочлена, обладают рядом свойств:

• •    любая MLS формируется путем циклического сдвига любой другой MLS;

• •    коэффициент корреляции р между двумя любыми MLS соответствует значению автокорреляционной функции (АКФ) любой из них и равен V N , где N - период MLS;

• •    все MLS равноудалены друг от друга в

пространстве на одинаковое кодовое расстояние

D . = 2 ^{к - 1} min

;

• •    MLS квазиортогональны.

Последнее свойство подчеркивается видом графика АКФ М-последовательности (см. рисунок 1).

Чем больше период MLS, тем ближе значение р ( t ) их АКФ к нулю и тем сильнее проявляются их ортогональные свойства.

Ортогональность, как продемонстрировано в работе [14], является важным условием организа- ции множественного доступа с кодовым разделением каналов. Для кодовых конструкций, используемых при решении данной задачи, достаточно выполнение условия ортонормированности, которая включает в себя ортогональность:

T

J S i ( t ) S j ( t ) dt =

1, i = j ,

0, i * j ,

где S i ( t ) и S j ( t ) - кодовые комбинации, которые должны использоваться в качестве адресных последовательностей. Физический смысл (1) состоит в том, что S i ( t ) и S j ( t) не оказывают влияния друг на друга и, следовательно, могут быть использованы в общем частотном спектре и на одном временном диапазоне.

Расширение спектра сигналов в CDMA предполагает последовательное умножение каждого их элемента на целые адресные последовательности. Результатом такого умножения будет замена каждого информационного символа «0» на прямую адресную последовательность, а символа «1» на инверсную адресную последовательность. Суммарный уплотненный сигнал представляет собой линейную сумму соответствующих элементов адресных последовательностей. Он передается в канал связи в биполярном виде.

Обработка суммарного сигнала на приеме производится для каждого абонента независимо от остальных. Фрагменты сигнала, содержащие сумму адресных последовательностей, поэлементно умножаются на все адресные последовательности, результат умножения суммируется и при необходимости нормируется. Таким образом, определяется уровень сигнала «+1» или «–1», который соответствует информационному элементу «0» или «1» в зависимости от установленного ранее правила замены униполярного сигнала на биполярный.

В работе [14] было предложено использовать последовательности максимальной длины в качестве адресных комбинаций вместо классических ортогональных функций Уолша, которые серьезно уступают М-последовательностям, в частности, по защите от фазовых сбоев. На основе MLS были построены ортогональные кодовые конструкции, которые представляют собой линейную сумму прямых и обратных М-последовательностей с разной начальной фазой.

Данные конструкции являются ортогональными по отношению ко всем адресным комбинациям, которые не входят в их состав. Также взаимная ортогональность возникает между самими конструкциями, которые содержат наборы MLS с отличающимися фазами.

Не составляет труда убедиться в их ортогональности, приведя пример использования MLS, построенных на основе многочлена P ( x ) = = x ⁴ + x + 1. Для этого вычислим скалярное произведение двух произвольных конструкций S 1 = = MLS 10 + MLS 12 (инверсная MLS с фазой е ¹⁰ суммируется с прямой MLS с фазой е ¹²) и S 2 = = MLS 5 + MLS 14 (прямая MLS с фазой е ⁵ суммируется с инверсной MLS с фазой е ¹⁴):

S 1 = ( -2 0 + 2 - 2 - 2 + 2000 - 200 + 2 + 2 0 ) ,

S ₂ = ( + 2 - 2 - 2 0 00 - 20 0 - 2 + 2 0 + 2 0 + 2 ) .

Фактически это соответствует передаче информационного элемента «0» по каналам 5 и 12 и передаче «1» по каналам 10 и 14. Коэффициент корреляции между ними, как и следовало ожидать, будет равен нулю:

р = ( -2 ) х 2 + 0 х ( -2 ) + 2 х ( -2 ) +

+ ( -2 ) х 0 + ( -2 ) х 0 + 2 х 0 +

+ 0 х ( -2 ) + 0 х 0 + 0 х 0 + ( -2 ) х ( -2 ) +

+ 0 х 2 + 0 х 0 + 2 х 2 + 2 х 0 + 0 х 2 = 0.

Теперь вычислим коэффициент корреляции для более сложных структур на основе MLS. Для примера возьмем:

S1 = MLS1 + MLS2 + MLS3 + MLS4 +

+ MLS6 + MLS7 + MLS8 + MLS9;

S 2 = MLS5 + MLS10 + MLS11 +

+ MLS12 + MLS14 + MLS14.

Результирующие сигналы S ₁ и S ₂ будут иметь вид:

( + 4 + 2 0 + 2 + 2 + 2 + 2 0 - 4 - 4 - 6 - 4 0 + 2 + 2 ) и

( + 4 - 4 - 4 - 4000000 + 4 - 4 + 4 0 + 4 ) соответственно.

Не составляет труда убедиться, что и в этом примере коэффициент корреляции будет равен нулю:

р = 4 х 4 + 2 х ( -4 ) + 0 х ( -4 ) + 2 х ( -4 ) +

+ 2 х 0 + 2 х 0 + 2 х 0 + 0 х 0 + ( -4 ) х 0 +

+ ( -4 ) х 0 + ( -6 ) х 4 + ( -4 ) х ( -4 ) + 0 х 4 +

+ 2 х 0 + 2 х 4 = 16 - 8 + 0 - 8 + 0 + 0 + 0 +

+ 0 + 0 + 0 - 24 + 16 + 0 + 0 + 8 = 0.

Таким образом, в работе [14] было предложено использовать выделенный канал (или каналы) для поддержания ортогональности кодовых конструкций. Это позволило однозначно выделить информацию абонентов, участвующих в обмене данными, и даже повысить урони сигнала на приеме.

Для каналов, которые напрямую не используются при передаче информации, а служат для баланса ортогональных свойств MLS, был предложен специальный термин – «фантомные».

Следующим шагом должна стать попытка применить метод обработки классических М-последовательностей двойственным базисом поля Галуа [16] в системе с фантомными каналами, что впоследствии обеспечит контроль целостности и фазы уплотненного сигнала.

Обработка многоуровневого сигнала двойственным базисом

Известно, что каждый ненулевой элемент поля Галуа можно представить в виде степени первообразного элемента ε, который, в свою очередь, является корнем характеристического многочлена P (x) степени k. При этом любые к последовательных элементов поля являются линейнонезависимыми над GF (2) и могут образовывать базис поля GF(2к). Любой элемент поля GF(2к) можно выразить через различные базисы, в том числе левый степенной и двойственный ему базис [3; 17].

Левый степенной базис представляет собой набор элементов поля: |^1, е, е2, кото-

рые можно обозначить в виде индексированного ряда:

а 1 , а ₂, а ₃, „., а _к ,

в то время как двойственный ему базис запишем в виде:

X1, X2, X3, ..., Xк.                   (3)

Ряды элементов (2) и (3) связаны условием:

T^{( Xa} j ⁾-и;

в котором функция-след T определяет сумму элементов поля, входящих в общий для них циклотомический класс [3; 17].

Главная задача двойственного базиса, удовлетворяющего условию (4), состоит в обработке MLS с целью вычисления начальной фазы. При этом элемент c e GF ( 2 ^k ) , порождающий данную последовательность, может быть определен по ее произвольному k -элементному участку ( S g S g . 1- S g . к - 1 ) следующим образом:

k c=е-g EX Л+.-i,

i = 1

где g – расстояние k -элементного участка от начала M -последовательности.

Классические прямые MLS представляют собой униполярные кодовые комбинации. Их обработка двойственным базисом приводит к формированию последовательных элементов поля Галуа, начиная с элемента, выполняющего роль начальной фазы М-последовательности. Инверсные MLS, принимающие непосредственное участие в формировании ортогональных структур, также являются рекуррентными последовательностями. По своей природе они опираются на тот же характеристический многочлен P ( x ) , но умноженный на ( x + 1 ) . Попытка обработать инверсную М-последовательность двойственным базисом, как показали эксперименты, приводит к появлению ряда элементов поля, среди которых обязательно присутствует аддитивная единица (нулевой элемент), полученная из инвертированного единичного k -элементного участка MLS.

Например, в случае с MLS 6 с начальной фазой е ⁶, построенной на основе P ( x ) = x ⁴ + x + 1, в дальнейшем инвертированной и обработанной двойственным базисом { е ¹⁴, е ², е , 1 } , получим ряд:

ее ⁸ е ⁷ e ² e^M 01 eWWeW .

Подобное расположение элементов поля является уникальным, так как ряд (6) обладает свойством формировать поле при сложении со своей копией, сдвинутой по фазе. Действительно, для примера произведем сложение элементов ряда (6) с его же элементами, сдвинутыми на 8 шагов вправо: ( е + е ¹⁰ ) =е ⁸, ( е ⁸ + е ¹² ) =е ⁹, ( е ⁷ + е ⁶ ) = = е ¹⁰, ( е ² +е ⁹ ) =е 11 , ( е ¹⁴ +е ⁵ ) =е ¹² и т. д.

Аналогичным образом поле формируется из последовательного набора своих же элементов, достаточно применить свойство дистрибутивности.

Отметим, что до сих пор двойственный базис использовался для обработки униполярных последовательностей [3; 17; 18]. Линейная сумма MLS требует перевода кодовых комбинаций в биполярный вид, иначе произойдет потеря данных. Как вариант, предлагается упомянутое выше правило, в соответствии с которым символ «0» заменяется на «+1», а символ «1» на «–1».

Сначала рассмотрим суммарный сигнал, полученный из двух прямых последовательностей MLS 1 и MLS 5 с начальными фазами е и е ⁵ соответственно:

S = ( + 2 0 - 2 + 2 0 0 - 2 0 - 2 0 0 0 0 - 2 + 2 ) .

Полученная структура может быть обработана двойственным базисом { е ¹⁴, е ², е , 1}, который применялся ранее в случае с униполярной последовательностью. Построим наглядные схемы обработки для первых трех ( t = 1, 2, 3) линейно независимых k -элементных участков, где маркерами отметим их уровни сигнала l (рисунок 2).

Для каждого k -элементного участка произведем сложение элементов поля, которые находятся на энергетических уровнях, равных по абсолютному значению L , т. е. определим суммы элементов поля на уровнях –1 и +1, –2 и +2 и т. д. Таким образом, схемы обработки (рисунок 2) можно свести к следующему результату (таблица 1).

Продолжив обработку следующих k -элементных участков, можно убедиться в появлении на обоих энергетических уровнях ряда элементов, совпадающего с рядом (6), но сдвинутого по фазе.

Также отметим дублирование элементов поля на энергетических уровнях, которое можно объ-

X /	Е14 +2	Е2 0	£       1 -2   +2	при 1= 1
+2	X		X	£М+1=£3
+ 1	X		X	£14+1=£3
-1			X	8
-2			X	8

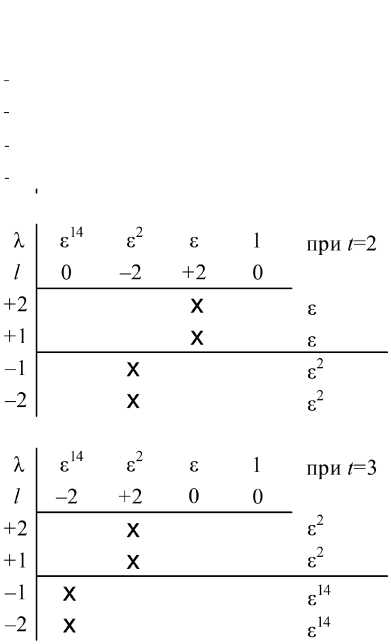
Рисунок 2. Обработка биполярного сигнала двойственным базисом яснить равномерным распределением энергии между двумя MLS, входящими в состав сигнала.

Теперь произведем аналогичную обработку сигнала, полученного при суммировании дву х ин версн ых последовательностей, например, MLS 6 и MLS 12 :

5 = ( + 2 + 200 - 2 0 + 2 0000 - 2 + 2 - 2 0 ) .

Видно, что структура данного сигнала совпадает с сигналом, рассмотренным в примере с прямыми последовательностями, отличие состоит только в начальной фазе. Не составляет труда убедиться, что обработка двойственным базисом в этом случае также формирует ряд (6).

Таким образом, можно сделать заключение, что результат обработки двойственным базисом биполярного сигнала, образованного любыми двумя прямыми или инверсными MLS с разными фазами, приводит к появлению одного ряда элементов поля, который, в свою очередь, совпадает с результатом обработки любой униполярной инверсной последовательности. Данное свойство можно объяснить влиянием, которое оказывает одна MLS на другую как в прямом виде, так и в инверсном.

При этом начальная фаза ряда, полученная при обработке суммарного сигнала, будет сдвигаться в зависимости от суммы элементов поля,

Таблица 1

L	t
	1	2	3
2	8 3 + 8 = 8 9	8 + 8 2 =8 5	8 2 +8 14 =8 13
1	8 3 + 8 = 8 9	8 + 8 2 =8 5	8 2 + 8 1 4 = 8 1 3

Таблица 2

L	t
	1	2	3	4	5	6	7
2	8 5 + 8 1 4 = 8 12	8 13	8 14	1	8	8 2	8 3
1	8 5 + 8 14 = 8 12	8 13	8 14	1	8	8 2	8 3

образующих М-последовательности. Это свойство проявится более наглядно в дальнейших примерах с сигналом, состоящим из прямых и обратных MLS. Обработка такого сигнала, в свою очередь, приведет к формированию элементов поля, определяемых суммой фаз входящих в его состав MLS.

Для примера произведем обраб отку сигнала, включающего в себя MLS₃ и MLS 10 с начальными фазами 8 3 и 8 ¹⁰ соответственно:

5 = ( -2 + 2 + 2 000 - 200 - 2 - 2 0 + 2 0 + 2 ) .

Проверим утверждение, которое гласит, что результат обработки двойственным базисом данной последовательности сформирует элемен- ты поля, начиная с элемента, равного их сумме

3 10

8 +8

= 8 ¹²

Действительно, используя схему, описанную выше (рисунок 3), получим прогнозируемый результат (таблица 2).

Теперь рассмотрим пример обработки более сложного сигнала, который состоит из нескольких ортогональных сигналов:

5 = MLS1 + MLS3 + MLS8 + MLS12 +

+ MLS4 + MLS5 + MLS9 + MLS14.

Таким образом, получим многослойную структуру:

5 = (0 - 2 + 2 0 + 2 0 - 6 + 6 +

+ 2 + 2 - 4 - 40 + 2 0).

Как и ожидалось, обработка первого k -элементного участка ( 0 - 2 + 2 0 ) определяет фазу, равную сумме элементов, порождающих MLS (рисунок 4):

8 +82 = 85;8    + 83 +88 + 812 + 84 +85 +89 + 814 = 85.

Более интересным случаем здесь является обработка участка, содержащего несколько уровней ( + 6 + 2 + 2 - 4 ) (рисунок 5), который,

X /	е14 -2	Е2 +2	£ +2	1 0	при /=1
+2		X	X		£2+£=£5
+ 1		X	X		£2+£=£5
-1	X				Е14
-2	X				Е14
X	е14	Е2	£	1	при /=2
/	+2	+2	0	0
+2	X	X			14, 2   13 £ +£ =£
+ 1	X	X			14, 2   13 £ +£ =£
-1					0
-2					0
X	е14	Е2	£	1	при /=3
/	+2	0	0	0
+2	X				Е14
+ 1	X				Е14
-1					0
-2					0
X	Е14	Е2	£	1	при /=4
/	0	0	0	-2
+2					0
+ 1					0 _______
-1				X	1
-2				X	1

Рисунок 3. Обработка суммы прямой и обратной последовательностей двойственным базисом согласно правилу, должен формировать элемент поля £12.

Из таблицы 3 видно, что значения фаз на четных и нечетных энергетических уровнях совпадают, их сумма соответствует ожидаемому элементу поля: £ ¹⁴ + £ 3 + е ¹¹ = £ ¹².

Заключение

Метод расширения спектра сигнала прямой последовательностью использует различные варианты кодовых комбинаций в зависимости от решаемых задач. Хорошие автокорреляционные функции таких комбинаций снижают вероятность фазовых сбоев, вместе с этим большое кодовое расстояние обеспечивает высокую помехоустойчивость. Важнейшим фактором совместного использования пригодных для расширения спектра последовательностей является их ортогональность. Именно это свойство позволяет произвести кодовое уплотнение и одновременно передавать независимые потоки информации в общей полосе частот.

X /	Е14 0	Е2 -2	£ +2	1 0	при /=1
+2			X		£
+ 1			X		£
-1		X			£2
-2		X			Е2

Рисунок 4. Обработка первого участка многослойного биполярного сигнала двойственным базисом

X 1	£14 + 6	£2 +2	£ +2	1	при /=8
+6	X				Е14
+5	X				£14
+4	X				£14
+3	X				£14
+2	X	X	X		£М+£2+£=£12
+ 1	X	X	X		£М+£2+£=£12
-1				X	1
-2				X	1
-3				X	1
—4				X	1

Рисунок 5. Обработка восьмого участка многослойного биполярного сигнала двойственным базисом

Таблица 3

L	t = 8
6	£ 14
5	£ 14
4	£ 14 + 1 = £ 3
3	£ 14 + 1 = £ 3
2	£ 12 + 1 =8 1*
1	£ 12 + 1 = £ 11

Как было показано в работе, М-последова-тельности позволяют строить многослойные ортогональные структуры, которые достаточно эффективно обрабатываются двойственным базисом поля Галуа. Результатом такой обработки являются двойные энергетические слои, которые содержат одинаковые элементы поля. Таким образом, сумма векторов поля на четных и нечетных уровнях является одинаковой и равной элементу поля, который, в свою очередь, определяет сумму фаз MLS, входящих в состав данной многослойной структуры.

Очевидно, что рассмотренные свойства могли бы обеспечить постоянный контроль передачи уплотненного сигнала. Любой сбой фазы или скачок уровня сигнала неизбежно приведет к разрыву ряда элементов поля, полученного в результате обработки последовательности двойственным базисом. При этом ортогональность на приеме позволит однозначно разделить сигнал на составляющие. Подобные результаты открывают обширные возможности в плане использования последовательностей максимальной длины при построении перспективных сверхнадежных систем передачи данных.

Исследование выполнено при финансовой поддержке РНФ в рамках научного проекта № 22-49-02023 «Разработка и исследование методов повышения надежности привязных высотных беспилотных телекоммуникационных платформ нового поколения».