Многоуровневая модель описания мартенситного превращения: формирование полиэдрической структуры мартенсита

Автор: Подседерцев А.Н., Кондратьев Н.С., Трусов П.В., Макаревич Е.С.

Журнал: Вестник Пермского национального исследовательского политехнического университета. Механика @vestnik-pnrpu-mechanics

Статья в выпуске: 2, 2024 года.

Бесплатный доступ

Многоуровневые модели неупругого деформирования, учитывающие эволюцию микроструктуры, являются перспективными для разработки технологий создания функциональных материалов-конструкций, имеющих оптимальные эксплуатационные характеристики. В работе обсуждается математическая формулировка прямой многоуровневой модели для описания неупругого деформирования представительного объема поликристалла (аналога макрообразца) с учетом формирования и эволюции мартенситной структуры в процессе превращения. В модель включено рассмотрение трех структурно-масштабных уровней. На макроуровне решается краевая задача, определяются поля напряжений, деформаций и других переменных модели. На мезоуровне-I рассматривается однородное зерно исходного аустенита, в котором за счет внешних воздействий происходит мартенситный переход. Для детализированного описания отклика материала на уровне зерна в рассмотрение вводится вспомогательный масштабный уровень - мезоуровень-II. На этом уровне явным образом исследуются геометрические особенности формирования пакетного мартенсита. Разработан оригинальный способ для описания полиэдрической структуры мартенсита, построение которой выполняется при достижении объемной доли новой фазы в зерне аустенита критического значения. Описание пакета как объединение полиэдров, состоящего из тонких пластин, позволяет ввести в модель геометрические характеристики элементов структуры, в частности границы пластинок и пакета, линейные размеры, объемы и др., дополнить их кристаллографическими ориентациями. Полученные геометрические характеристики мартенситного пакета с последующей обработкой передаются на уровень отдельного зерна. Это позволяет более детально учитывать реализующиеся в процессе взаимодействия фаз механизмы деформирования и упрочнения. Приводятся результаты формирования полиэдрической структуры пакета мартенсита в стали 08Х18Н10 (AISI 304) в численных экспериментах по одноосному деформированию при комнатной температуре и скорости деформирования 10-5c-1.

Еще

Мартенситное превращение, многоуровневые физически-ориентированные модели, неупругое деформирование, пакетный мартенсит, критерий фазового превращения

Короткий адрес: https://sciup.org/146282919

IDR: 146282919 | DOI: 10.15593/perm.mech/2024.2.09

Текст научной статьи Многоуровневая модель описания мартенситного превращения: формирование полиэдрической структуры мартенсита

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2024PNRPU MECHANICS BULLETIN

В современной промышленности широко используются методы термомеханической обработки (ТМО) большинства деталей и конструкций из поликристалли-ческих металлов и сплавов [1–4]. Эффективное проведение ТМО сплавов требует совершенствования технологических режимов. В этом контексте актуальной задачей является разработка физически ориентированных математических моделей для корректного описания отклика материала с учетом физических механизмов и их носителей. Эти модели позволят корректно описывать формирование и изменения микроструктуры и свойств материала при различных термомеханических воздействиях, что, в свою очередь, позволит оптимизировать существующие и создавать новые методы ТМО для получения конечных изделий с требуемыми эксплуатационными характеристиками. В ходе ТМО металлов и сплавов реализуются различные физические механизмы и процессы, сопровождающие неупругую деформацию; к числу наиболее значимых относятся твердотельные фазовые превращения, рекристаллизация, возврат, двойникование и другие [5; 6]. В процессе ТМО заготовкам из сплавов, которым свойственен полиморфизм, физическими механизмами перестроения структуры и релаксации упругих напряжений являются фазовые переходы, в частности мартенситное превращение, которое приводит к существенным изменениям в фазовом составе и микроструктуре материала [7; 8]. Мартенситное превращение наблюдается в титановых [9–12], медных [13; 14], никелевых [15; 16] и других сплавах [17–20]. Следует отметить, что наиболее широко эта способность материалов распространена в сплавах на основе железа [21–23]. Образование мартенсита представляет собой бездиффузи-онную перестройку исходной кристаллической решетки метастабильного аустенита, например гранецентрированной кубической решетки (ГЦК) в низкоуглеродистых сплавах на основе железа, в объемно-центрированную кубическую (ОЦК) решетку мартенсита [24; 25]. Мартенсит, в отличие от других фазовых компонентов, характеризуется высокой твердостью, однако пластинки новой фазы обладают хрупкостью, по сравнению с другими фазами. Мартенсит имеет определенную ориентацию кристаллической решетки относительно родительской фазы согласно известным ориентационным соотношениям [26; 27]. При этом мартенситная фаза в зависимости от химического состава материала и параметров воздействия имеет различную геометрическую форму (пластинки, линзы и др.) [28]. Таким образом, структура поликристаллов, содержащих мартенсит, представляет собой уникальный «природный композит», обладающий потенциалом для создания изделий с повышенными эксплуатационными характеристиками. Макросвойства образца напрямую зависят от внутренней структуры, в том числе от композитной структуры мартенсита.

Мартенситное превращение реализуется во многих процессах ТМО, таких как закалка, ковка, прокатка, волочение и другие [29–32]. Существующие методы ТМО металлов имеют значительный потенциал для создания необходимой для эксплуатации структуры, следовательно, свойств материала в процессе его обработки, изготовлении конечных изделий [33; 34]. Для решения этой проблемы необходимы математические модели, основанные на глубоком физическом описании поведения стали при реализации твердотельных фазовых превращений в целом и мартенситного перехода в частности.

Мартенситные превращения изучаются достаточно долгое время, и для его моделирования применяются различные подходы и методы. Наиболее простыми являются модели макрофеноменологического типа [35–38]. В основе таких моделей лежит аппроксимация экспериментальных данных, полученных при исследовании мартенситных превращений, которая позволяет определить долю образовавшегося мартенсита в зависимости от внешних воздействий, при этом подобные модели применимы в узких диапазонах температурных и механических воздействий. Также подобный подход не позволяет описать формирование структуры мартенситной фазы, поскольку не учитывается гетерогенный характер зарождения мартенсита и развитие отдельных элементов новой фазы. Более эффективным способом исследования эволюционирующей структуры и отклика материала являются многоуровневые модели неупругого деформирования с внутренними переменными. Модели этого класса, основанные на описании физических механизмов на различных масштабных уровнях, являются более универсальными и точными [39–43].

Для описания физических механизмов и их носителей в многоуровневые модели вводятся внутренние переменные и эволюционные соотношения для них, которые описывают движущие силы фазового перехода, структуру материала, объемную долю различных вариантов мартенсита и др. Существует три основных класса этих моделей: статистические, прямые, самосогласованные. В статистических моделях, как правило, рассматривается макроточка – представительный объем макроуровня, состоящий из совокупности отдельных кристаллитов (зерен, субзерен, фрагментов), не связанных пространственно, но объединенных гипотезой связи (Фойгта, Рейса, Крёнера и др.) [44–46]. Такие модели являются вычислительно эффективными, процесс фазового превращения в них обычно описывается с использованием «смесевой» модели, т.е. для учета новой фазы вводятся дополнительные параметры состояния или переменные модели, характеризующие особенности многофазного материала «в среднем» (например, объемная доля мартенсита). В самосогласованных моделях рассматривается одиночное включение кристаллита (зерна, субзерна, фрагмента) в окружающую матрицу с осред-ненными физико-механическими характеристиками материала [47–50]. В самосогласованных моделях основным недостатком в применении к проблеме мартенситного превращения является представление окружающего континуума матрицей с осредненными свойствами, которая не отражает реального взаимодействия микроструктуры с окружением. Прямые модели являются наиболее точными, но и ресурсоемкими [51–53]. В прямых моделях решаются краевые задачи для определения полевых величин [39; 54]. Применение прямых моделей к рассматриваемой проблеме неупругого деформирования многофазного материала позволяет явно учесть неоднородность полей напряжений и температуры из решения краевой задачи и влияние анизотропии свойств на макроотклик материала. Однако существует проблема явного прямого моделирования структуры мартенсита, в связи с чем в большинстве моделей, применяемых для описания мартенситного превращения, также используется «смесевая» модель для описания влияния мартенситной фазы на свойства материала [51–53].

Таким образом, основным недостатком существующих моделей является отсутствие возможности детального учета влияния текущего состояния мартенситной структуры на отклик материала, которое наблюдается экспериментально [55–61]. Явное моделирование структуры новой фазы позволит более корректно с физической точки зрения описать мартенситное превращение. На основе данных о структуре мартенсита можно детально учесть реализующиеся в процессе взаимодействия фаз механизмы деформирования и упрочнения.

В рамках данного исследования рассматривается пластинчатый мартенсит, который имеет сложную иерархическую структуру. Он состоит из тонких сдвой-никованных пластинок [62], которые, как правило, располагаются параллельно друг другу. Эту структуру можно наблюдать на различных масштабах мартенсита [63]. Между аустенитом и мартенситом образуется совместная граница, называемая габитусной плоскостью, которая обладает минимальной поверхностной энергией [64; 65]. Набор пластинок с одинаковой ориентацией называют блоком [66]. В свою очередь блоки c параллельными габитусными плоскостями, расположенные рядом, называют пакетами. Существуют модели, способные явно описать зарождение мартенсита и формирование мартенситной структуры, например с использованием метода клеточных автоматов, в том числе на основе экспериментальных микрофотографий [53; 67–69], или метода фазового поля на нижних масштабах для описания зарождения мартенсита [70–72], и др. Однако применяемые методы обладают рядом недостатков; в частности, объемная доля мартенсита и структура, получаемые в процессе моделирования с применением метода клеточных автоматов, напрямую зависят от правил перехода и размеров ячеек [53; 69], а метод фазового поля детально и точно описывает зарождение мартенситной фазы, но является весьма ресурсоемким для описания всей совокупности пластин в зерне [71; 72]. Таким образом, актуальной задачей является моделирование мартенситной структуры, под которым подразумевается разработка концептуальной и математической постановки, в рамках моделей неупругого деформирования с учетом физических механизмов мартенситного превращения, а также разработка эффективных алгоритмов для формирования мартенситной структуры.

Целью исследования является разработка прямой математической многоуровневой модели неупругого деформирования с учетом мартенситного превращения и эволюции структуры новой фазы.

1. Модель неупругого деформирования с учетом формирования мартенситной структуры

В работе предлагается модель для описания мартенситного превращения в стали 08Х18Н10 (AISI 304) с пакетной структурой мартенсита. Данный тип мартенсита наиболее часто встречается в сплавах на основе железа и играет важную роль в процессах ТМО высокопрочных материалов. Его образование характерно для сталей с низким содержанием углерода и повышенным содержанием легирующих элементов, таких как Ni и Mn [73]. В рассматриваемой стали пакетный мартенсит образуется под действием внешней нагрузки при температуре ниже мартенситной точки [73], что подтверждается экспериментальными данными исследования микроструктуры [73–75]. Экспериментально показано, что мартенсит образуется гетерогенно, т.е. образование новой фазы начинается со «стартовых» точек, называемых зародышами [76–78]. Зародышами мартенсита обычно является

Ориентационные соотношения Курдюмова –

совокупность дефектов упаковки относительно решетки родительской фазы аустенита. Такая совокупность дефектов упаковки представляет собой небольшую область (с характерным размером порядка 40 нм [79]), имеющую кристаллическую решетку с мартенсита. Область вокруг зародыша наиболее подготовлена для фазового превращения. Мартенсит прорастает в форме пластинок со скоростями порядка скорости звука в таких направлениях, что наиболее плотноупакованные плоскости и направления в кристаллической решетке аустенита параллельны наиболее плотноупакованным плоскостям и направлениям мартенсита, согласно ориентационным соотношениям Курдюмова – Закса, приведенным в табл. 1 [63].

Зародыши новой фазы обычно образуются на пересечениях полос сдвига [78; 80]. Широко принятый многими исследователями механизм трансформации решетки аустенита в решетку мартенсита, основанный на двойном простом сдвиге и образовании дефекта упаковки, описан в работах [81–83]. Образование зародышей мартенсита обычно имеет случайный характер [84]. Оно происходит в результате локальной концентрации напряжений, которые играют ключевую роль в поддержании и развитии зародышей мартенсита, автокаталитически инициируя процесс образования новых областей трансформации аустенита [84; 85]. В результате возникает рост и последующее слияние зародышей мартенсита [85].

Таблица 1

Закса между аустенитом (γ) и мартенситом (α)

Table 1

Вариант №

Параллельные плоскости

Параллельные направления [γ] || [α]

Вариант №

Параллельные плоскости

Параллельные направления [γ] || [α]

( 111 ) Y II ( 011 ) a

’ 101 "

t ¹¹¹ ’

( 111 ) y || ( 011 ) a

’ 011 ’

I ¹¹¹ ’

"101 "

I ¹¹¹ ’

’ 011 ’

I ¹¹¹

"011

’^I

’ 101 ’

[ ¹¹¹ ’

011 ’

I ¹¹¹

’ 101 ’

[ ¹¹¹

"110 "

’111 "

[ 110 ] II

111 ’

"110 "

f ¹¹¹ ’

[110] ||

¹¹¹ ]

( 111 ) y || (011) a

"101 ’

’111 ’

( 111 ) y II ( 011 ) o

’ 110 "

[ ¹¹¹ ]

’101 "

f ¹¹¹ ’

’ 110 ’

[ ¹¹¹ ’

"110 "

f ¹¹¹ ’

’011

[ ¹¹¹

’110 ’

011 ’

’ 111

]

[ 011 ] I

111 ’

[101] ||

111 ’

[ 011 ] II

¹¹¹ ]

[101] ||

¹¹¹ ]

Kurdyumov – Sachs orientation relationships between austenite (γ) and martensite (α)

Зародыши мартенсита вырастают в форме пластинок толщиной, как правило, порядка 0,2–1 % от среднего диаметра зерна [59; 66]. Предполагается, что пластинки мартенситной фазы прорастают неравномерно и могут иметь различную толщину, это утверждение подтверждено экспериментально [22; 73]. В данной работе предполагается равномерное распределение толщин пластинок. Для пакетного мартенсита характерно образование кластеров, называемых блоками, состоящих из параллельных близко ориентированных тонких (по сравнению с толщиной пластин) двойниковых мартенситных пластин [62]. Толщина блока составляет порядка 2–10 % от среднего диаметра зерна [59; 66]. В свою очередь, блоки, расположенные вблизи друг друга, которые содержат пластинки с параллельными габитусными плоскостями, называют пакетом. Размеры пакетов, как правило, составляют около 40 % от среднего диаметра зерна. Пластинки новой фазы образуют пакеты 4 различных вариантов с различной ориентацией относительно родительского зерна. В каждом пакете может быть расположено до 6 различных вариантов пластинок мартенсита (см. табл. 1). Таким образом, двухфазное зерно после образования мартенсита представляет собой конгломерат из пакетов мартенсита. Пакеты и блоки разделены большеугловыми границами [58; 59; 86]. Каждый блок состоит из двойниковых пластинок мартенсита, которые могут на начальном этапе быть разделены тонким слоем родительской фазы (рис. 1). Экспериментальные данные свидетельствуют, что при деформации более 10 % остаточный аустенит между пластинками мартенсита может полностью трансформироваться в новую фазу.

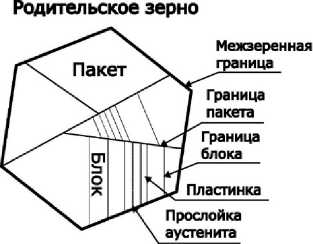
Рис. 1. Схематичное представление мартенситной структуры внутри родительского зерна

Fig. 1. Schematic representation of the martensitic structure within the parent grain

В рамках настоящего исследования для формирования представленной структуры мартенсита рассматривается физическая прямая модель для анализа неупругого поведения представительного объема поликристалла. Для решения поставленной проблемы в модели выделяются три структурно-масштабных уровня – макроуровень, ассоциированный с представительным макрообъемом поликристалла, мезоуровень-I – отдельным зерном поликристаллического агрегата, и мезоуровень-II – пакетом мартенсита. На макроуровне ставится и решается краевая задача неупругого деформирования и теплопроводности с определенными начальными и граничными условиями. Следует отметить, что прямое мартенситное превращение является экзотермическим процессом [87]. Как и при пластическом деформировании, в процессе мартенситного превращения часть свободной энергии переходит в тепло, однако вклад пластических деформаций и мартенситного превращения в изменение температуры можно считать незначительным. При деформировании до 20 % и образовании мартенсита с объемной долей около 6 %, по приблизительным оценкам, изменение температуры составляет менее 1 °С. Решение краевой задачи на макроуровне позволяет определить поля напряжений, деформации и температуры, которые являются механическими (градиент скорости перемещений) и термическими (температура) воздействиями для каждого элемента мезоуровня-I в каждый момент времени. Подробно с математическими постановками многоуровневых моделей можно ознакомиться в [42].

На мезоуровне-I рассматривается отдельное однородное зерно поликристаллического агрегата, где решается задача определения напряженно-деформированного состояния. На этом уровне для учета новой фазы используется смесевая модель, в рамках которой введены дополнительные параметры состояния, такие как объемная доля мартенситной фазы для каждой трансформационной системы, ориентация мартенсита относительно родительской фазы. Элемент мезоуровня-I, в свою очередь, может включать в себя элементы мезоуровня-II. Элемент мезоуровня-II генерируется в процессе мартенситного превращения и ассоциируется с пакетом, для которого явным образом конструируется геометрия (форма и размеры) мартенситной структуры на основе данных модели мезоуровня-I. Мезоуровень-II вводится для уточнения отклика материала за счет явного описания механизмов взаимодействия фаз. Для этого предполагается на мезоуровне-I ввести дополнительные переменные модели, определяемые с применением подмодели мезо-уровня-II (геометрического представления пакета мартенсита). Схема, иллюстрирующая взаимосвязь структурно масштабных уровней, представлена на рис. 2.

Зерно

Пакет

Толщины и количество пластинок мартенсита

Градиент скорости перемещений, температура

11редставител ьный макрообъем

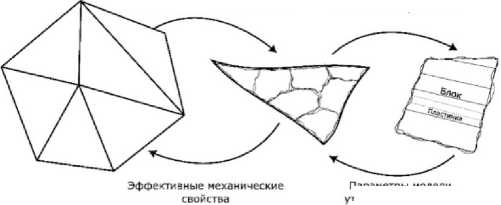
Параметры модели, уточненение отклика

Рис. 2. Схема и связь структурно-масштабных уровней многоуровневой модели

Fig. 2. Scheme and connection of multilevel model structural-scale levels

Из решения краевой задачи на макроуровне в каждый момент времени t определяются механические и термические воздействия: градиент скорости перемещений V v ( t ) и температура 0 ( t ) для каждого элемента мезо-уровня-I. Температура, скорость изменения температуры, НДС в каждый момент процесса в каждом зерне принимаются однородными. Зерна в поликристалле отличаются ориентацией кристаллической решетки, фазовым составом (в настоящей работе полагается, что в отсчетной конфигурации весь представительный объем занят аустенитом) и микроструктурой.

На мезоуровне-I решается задача определения напряженно-деформированного состояния зерна и соответствующих внутренних переменных модели с применением расширенной статистической модели. Определенные в ходе решения отклик зерна и эффективные механические свойства возвращаются на макроуровень. Математическая формулировка модели мезоуровня-I содержит следующие соотношения:

ст cr = п: (V vT - и - z"),(1)

Ns24

zn = £ Y(k b k >n< k) + £ 4 (₽№<» + a0,(2)

k=1

T(k )= b(k )n(k ) : O ,(3)

< ( k ) Л m

Y(k) = Yо h ( t(k)- Tk)),(4)

⁽ ^k )

V ^Т с J

N s

TCk ) = £ h (jY(j),(5)

. i = 1

h ( k ) = [ q at + (1 — q at )§ ( kl ) ] h ⁽ l ) , h⁽ l ) = h о 1 — < ) / т s _a t |a , (6)

и = o • oT = I x (k3k1k2 - k2k1k3 + k,k2k3): le,(7)

ze = z - zin,(8)

£ ( P )

S m

S ₀ tanh

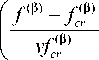
если f(в > f(₽) cr иначе

Соответствующие начальные условия заданы следующим образом:

’| _t = ₀ = ^ o , o _t = ₀ = ° o , ^т? )| _t = ₀ = , Y? )| _t = 0 = y S g . ⁽¹⁰⁾

Здесь σ0 – тензор напряжений Коши в начальный момент времени предполагается нулевыми, так как в естественной конфигурации отсутствует фаза мартенсита; o0 – тензор ориентации элемента мезоуровня-I (на макроуровне предполагается равномерное распределение ориентаций зерен); 40 - начальные критические напряжения сдвига по системам скольжения соответст- вуют критическим напряжениям фазы аустенита; y^k) -начальные сдвиги по системам скольжения в естественной конфигурации отсутствуют.

В математической постановке используются следующие обозначения: σ – тензор напряжений Коши мезоуровня; ст cr = d ст / dt + ст • и - и • ст - коротационная производная тензора напряжений; z ^e , z ⁱⁿ – упругая и неупругая составляющие меры скорости деформации мезоуровня; п – тензор упругих свойств рассматриваемого зерна, компоненты которого п ^ijmn определены и постоянны в актуальном базисе жесткой подвижной системы координат, вращающейся со спином ω [88]; I – единичный тензор; k _i – векторы базиса жесткой подвижной системы координат [89]; l ^e – упругая составляющая транспонированного градиента скорости перемещений; b ⁽ ^k ) , n ⁽ ^k ) - единичные векторы направления скольжения и нормали к плоскости k -й системы сколь-

( k ) ( k )

жения; N s - число систем скольжения; т ', т' У - сдвиговые и критические напряжения k -й системы внутризе-ренного скольжения; в законе упрочнения [90; 91] учитываются взаимодействия подвижных дислокаций с дислокациями леса (5) (в (5) за счет дополнительных слагаемых может быть учтено упрочение систем скольжения в результате взаимодействия подвижных дислокаций аустенита с границами мартенситной фазы [92–94] и эффект Холла – Петча [66; 95]); h ⁽ ^kl ⁾ – матрица, описывающая упрочнение кристалла за счет взаимодействия дислокаций с дислокациями леса; q lat – параметр латентного упрочнения; τ _sat – напряжения насыщения; h 0 , a –

• ( k )

параметры, описывающие упрочнение материала; γ – скорость сдвига по k -й системе; Y ₀ - скорость сдвига по системе скольжения при достижении касательным напряжением критического напряжения сдвига; m – показатель скоростной чувствительности материала; H – функция Хевисайда; 5⁽ ^kl ) - дельта Кронекера; векторы т ⁽ ^в ⁾ и s ⁽ ^e ⁾ задают трансформационную систему: вектор нормали к инвариантной плоскости и вектор сдвига (в отличие от кристаллографических сдвигов, s не ортогонально m , компоненты этих векторов в ОЦК кристалле аустенита образуют 24 трансформационные системы) [96]; 4 м , ^ М³ - объемная доля мартенсита и ее скорость изменения; f c ® - критическое значение движущей силы на трансформационной системе; V - материальный параметр; 4₀ - параметр материала, определяющий скорость изменения объемной доли мартенсита при достижении движущей силой критического значения. Параметры закона упрочнения ( q lat , τ _sat , h ₀, a ), соотношения для скорости сдвигов по СС ( Y ₀ , m ) и соотношения для скорости изменения объемной доли мартенсита ( V , 4 0 ) в общем случае определяются в ходе идентификации модели.

Движущая сила, используемая для определения скорости изменения объемной доли мартенситной фазы (9) на каждой трансформационной системе, представлена в виде двух слагаемых - термической f th ^e ) и механической f m ^e ) составляющих [44; 45]:

f ⁽ ^в ⁾ = f m e + fr

f e = J f p T • f e T • _o • f e - T • f p - T • f p : ( s ^(e) m ^(e)) + + 2 ( |( f e T • f e - 1 ): й : 2 ( f e T • f e - 1 ) ) ,

( f 1 I f. =Po(h<₽) — hA)|0ln|^ I — (0 — 0t) I +

I 10 T J J

+ Po gM(0-0T), 0T где hA - теплоемкость аустенита; h(в)- теплоемкость мартенсита; 0T - температура мартенситного перехода при отсутствии упругих деформаций; 0 - температура; gM – скрытая теплота мартенситного перехода; fe , f p – упругая и пластическая составляющая градиента места соответственно; р0 - плотность аустенита; J - изменение объема за счет образования новой фазы; I – единичный тензор. Представление движущей силы (11) введено согласно разложению свободной энергии Гельмгольца на сумму механической, которая включает в себя энергию упругих и трансформационных деформаций, термической энергии, энергии межфазной поверхности и энергии дефектов [97]. Последние два слагаемых для пакетного мартенсита полагаются малыми [44; 45].

В предложенной модели структура мартенсита определяется внутренними переменными: объемы пластинок, геометрические характеристики плоских участков границ (нормали, координаты центров и площади фасеток), указатели на соседние пластинки к рассматриваемой пластинке. Далее описан способ формирования геометрической структуры мартенсита. После достижения критического значения объемной доли мартенсита на трансформационных системах, которые соответствуют определенному варианту пакета, проводится геометрическое описание мартенситной структуры – генерируется элемент мезоуровня-II (пакет). Критическое значение объемной доли новой фазы на трансформационных системах, которые имеют параллельные габитусные плоскости, устанавливается в вычислительных экспериментах и равно 6 % от объема зерна. В связи с тем, что установлена зависимость между размером зерна и пакета мартенсита [98], можно определить, что на одно зерно приходится около 15 пакетов, следовательно, критическое значение объемной доли соответствует необходимому количеству мартенсита для формирования структуры одного пакета. Генерация полиэдрической структуры пакета мартенсита на этом уровне происходит с исполь- зованием программного обеспечения (ПО) Neper [99; 100]. Входными данными для Neper являются количество и относительные толщины пластинок в пакете.

В настоящей работе предполагается, что пакет имеет форму куба. В процессе генерации структуры пакет «разрезается» на пластинки заданной толщины. Средняя толщина пластинок мартенсита не зависит от условий нагружения и размера зерна родительской фазы, но зависит от содержания углерода в родительской фазе, что подтверждается экспериментальными данными [59; 66; 98]. Полагая углерод распределенным внутри родительского зерна равномерно, считается, что пластинки прорастают вдоль всего пакета, а их средняя толщина одинакова и фиксирована, вне зависимости от варианта мартенсита. Относительная средняя толщина пластинки d ' _l определяется отношением физической средней толщины пластинки d_l к физическому размеру пакета мартенсита d_p :

d ' i = dr . (14) d p

Размер пакета мартенсита, согласно экспериментальным данным [98], имеет линейную зависимость от размера зерна d_g , для учета этого вводится феноменологическое соотношение, описывающее зависимость среднего размера пакета от размера зерна [98]:

dp = Pds , (15)

где p - параметр модели.

С целью определения количества пластинок в пакете необходимо вычислить среднюю объемную долю пластинки, относительно объема зерна. Предполагается, что пластинку можно считать параллелепипедом с длинами сторон dl x dp x dp . Предполагая, что зерно имеет форму куба, можно представить соотношения для средней объемной доли пластинки ^'M мартенсита в следующем виде:

d,d d lpp dg3

Количество пластинок Л ^ на трансформационной системе β вычисляется как отношение объемной доли мартенсита системы β к относительному объему пластинки мартенсита:

( в )

N (W₌S M_ l ^м

Для получения целого количества пластинок проводится округление N ^), считая остаток объемной доли мартенсита малой величиной.

По найденным значениям внутренних переменных мартенситной структуры пакет генерируется в ПО Neper.

Выходными данными генерации структуры является полиэдрическая структура и геометрические характеристики полиэдров, которые ассоциируются с пластинками мартенситной фазы: объемы пластинок, плоские участки границ (нормали, координаты центров и площади фасеток), указатели на соседние пластинки к рассматриваемой пластинке и др.

Пластинки, образующиеся на различных трансформационных системах, имеют различную ориентацию относительно родительской фазы [63]. Каждой пластинке мартенсита, сформированной в рамках элемента мезо-уровня-II, приписывается собственная ориентация кристаллической решетки. Ориентация пластинки относительно родительского зерна выбирается согласно трансформационной системе так, чтобы наиболее плотноупакованные плоскости и направления кристаллической решетки родительской фазы и пластинки мартенсита были параллельны [27]. Ориентационные тензоры для всех 24 трансформационных систем являются известными [63]. Малые отклонения ориентации от соотношений Курдюмова – Закса не учитываются. После того как полиэдрическая мартенситная структура сформирована, полученные геометрические характеристики структуры передаются обратно в расширенную статистическую модель мезоуровня-I для уточнения отклика материала. В дальнейшем предполагается на основе полученных геометрических характеристик учесть механизмы деформирования и упрочнения за счет межфазного взаимодействия.

2. Результаты моделирования и их анализ

В работе исследуется неупругое деформирование монокристалла нержавеющей стали 08Х18Н10 (AISI 304). Химический состав стали представлен в табл. 2.

Таблица 2

Химический состав стали марки 08Х18Н10(%)

Table 2

Chemical composition of steel grade AISI 304 (%)

Стандарт	C	Si	Mn	P	S	Cr	Ni
ASTM A240	<0,080	<0,75	<2,0	<0,045	<0,030	18,0– 20,0	8,0– 10,50

Рассмотрим результаты, полученные в рамках подмодели мезоуровня-I, краевая задача на макроуровне при этом не решается. Принимается следующая гипотеза о воздействиях: с макроуровня полагаются известными кинематические воздействия, согласно гипотезе Фойгта. Считается предписанным градиент скорости перемещений ∇ ^ˆ V , который соответствует квазиодноосному деформированию:

~ Ё Ё

V V =^Ё k 01 k 01 - 2 k 02 k 02 - 2 k 03 k 03 , (18)

где k ₀ _i = k ⁱ ₀ – ортонормированный базис лабораторной системы координат, Ё - скорость предписанной деформации.

Далее приведены результаты вычислительных экспериментов при скорости деформирования Ё =10 ^- ⁵ с ^- ¹ и температуре θ = 773 К. Разрабатываемая модель апробирована для квазистатического нагружения. Известно, что в исследуемом диапазоне скоростей деформирования наблюдается слабая зависимость отклика материала от скорости нагружения. Использовались параметры, приведенные в работах других исследователей: компоненты тензора упругих свойств п₁₁₁₁ , п₁₁₂₂ , п₁₃₁₃ , начальный предел текучести τ _с ₀ и параметр скоростной чувствительности m представлены в [103]. Материальные параметры для критерия фазового превращения f_c ⁽ _r ^β ⁾ , ξ ₀ , v были определены на основе анализа литературных данных [44; 45]. Для формирования мартенситной структуры необходимы значения среднего размера зерна d_g и средней толщины пластины d_l , которые приведены в статьях [104; 105]. Используемые параметры математической модели представлены в табл. 3. Идентификация параметров для закона упрочнения аустенита проведена с использованием экспериментальных данных, приведенных в статье [106].

Таблица 3

Параметры материала математической модели мезоуровня-I

Material parameters of the mesolevel mathematical model-I

Table 3

Параметр	Значение	Источник
^п 1111	204,6 ГПа	[103]
^п 1122	137,7 ГПа	[103]
^п 1313	126,2 ГПа	[103]
τ с 0	159 МПа	Процедура идентификации
τ sat	800 МПа	Процедура идентификации
h 0	135 МПа	Процедура идентификации
a	1,4	Процедура идентификации
q lat	1,4	Процедура идентификации
• γ₀	10 ^–5 c ^–1	[103]
m	50	[103]
^ξ 0	3 · 10 ^–3 c ^–1	[45]
( β ) f_cr	336 МПа	Процедура идентификации
v	0,17	[45]
^dl	0,3 мкм	[104]
^dg	50 мкм	[105]
μ	0,4	[98]

На рис. 3 представлена зависимость интенсивности напряжений от интенсивности деформаций, полученная в вычислительном эксперименте. Наблюдается приемлемое соответствие расчетной кривой и экспериментальных данных [106]. При заданных условиях нагружения образуется не более 8 % мартенсита, поэтому в математической постановке для зерна не учитывается влияние мартенсита. Отклонение результатов численного эксперимента по отношению к данным натурного количественно не превышает 3 % (максимальное значение в точке).

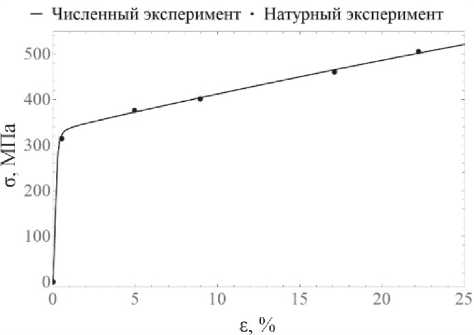
Рис. 3. Зависимость интенсивности напряжений от интенсивности накопленных деформаций для образца из поликристаллической стали 08Х18Н10, точки соответствуют эксперименту [106]

Fig. 3. Dependence of stress intensity on the intensity of accumulated strains for a sample made of polycrystalline steel grade 08Х18Н10, points corresponds to experiment [106]

На рис. 4 представлена зависимость объемной доли мартенсита от интенсивности деформаций, полученная в вычислительном эксперименте [107]. Наблюдаемое отклонение от экспериментальных данных [107] составляет не более 10% (максимальное значение в точке).

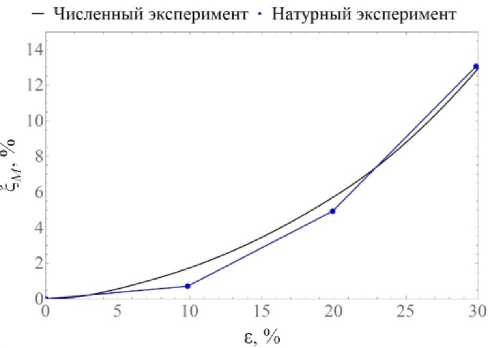
Рис. 4. Зависимость объемной доли мартенсита от интенсивности накопленных деформаций в фазе аустенита, синий график соответствует эксперименту [107]

Fig. 4. Dependence of the volume fraction of martensite on the intensity of accumulated strains in the austenite phase, blue graph corresponds to experiment [107]

Проведены вычислительные эксперименты с различными направлениями оси деформирования относительно кристаллографических осей монокристалла. В табл. 4 отражено распределение мартенсита по различным трансформационным системам в различных численных экспериментах. Важно отметить, что в процессе деформации на начальной стадии образуется новая фаза на трансформационных системах с одинаково ориентированной габитусной плоскостью, а при дальнейшем деформировании активируются другие трансформационные системы. Количество активируемых трансформационных систем определяется механической движущей силой. Собранный набор пластинок мартенсита позволяет создать пакет новой фазы.

В процессе растяжения в направлениях [ 123 ] (рис. 5, а ), [ 111 ] (рис. 5, b ), [ 123 ] (рис. 5, c ) при достижении 6 % объемной доли вычислялось количество пластинок новой фазы с одинаковой габитусной плоскостью. Распределение толщин пластинок предполагается равномерным в диапазоне от 0,2 мкм до 0,4 мкм (отклонение от средней толщины пластинки d_l = 0,3 мкм не более 33 %). Оси пакета (куба) направлены вдоль осей КСК. По полученным данным сформирована геометрическая структура пакета мартенсита с использованием ПО Neper, которая представлена на рис. 5. В данном исследовании было проведено формирование одного пакета мартенсита на начальной стадии, но при дальнейшем деформировании не составит труда проводить процедуру генерации пакетов в произвольный фиксированный момент времени. Получено приемлемое качественное соответствие экспериментальным данным.

Заключение

В настоящей статье описывается концепция прямой математической модели неупругого деформирования поликристалла с учетом формирования и эволюции структуры новой фазы в процессе мартенситного превращения. Подробно изложен разработанный оригинальный способ геометрического описания структуры новой фазы. В работе приведена формулировка прямой математической модели неупругого деформирования с учетом мартенситного превращения. Предложена и реализована подмодель мезоуровня-I. Изложен способ описания формирования мартенситной структуры на мезоуровне-II с применением геометрического подхода для последующей передачи полученных характеристик пластинок новой фазы в статистическую модель мезо-уровня-I с целью уточнения его отклика. Основным преимуществом предложенной модели, по сравнению с существующими, является явное введение в рассмотрение мартенситных пластин, что позволяет учитывать их взаимодействие с окружением, соседними пластинами и родительской фазой.

Таблица 4

Преимущественные системы трансформации мартенсита в зависимости от направления деформирования

m =[0,122, -0,837, 0,533]

m =[0,533, 0,122, -0,837]

m =[-0,837, 0,533, -0,122]

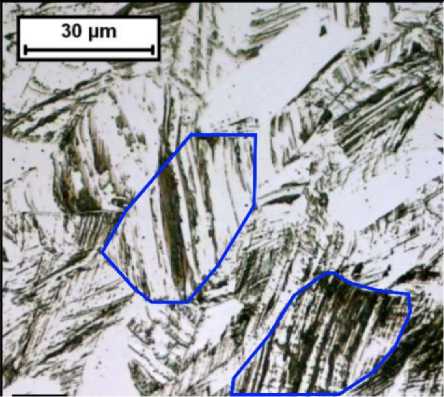
Table 4

Predominant transformation systems for martensite growth depending on deformation direction

Направление деформирования	Активные трансформационные системы						Доля мартенсита, %
Направление деформирования	Вектор нормали габитусной плоскости ( m )			Вектор сдвига (s)			Доля мартенсита, %
[100]	-0,837	-0,533	0,122	-0,286	0,426	0,112	0,75
	-0,837	0,533	0,122	-0,286	-0,426	0,112	0,75
	-0,837	0,122	-0,533	-0,286	0,112	0,426	0,75
	-0,837	0,122	0,533	-0,286	0,112	-0,426	0,75
	-0,837	-0,122	0,533	-0,286	-0,112	-0,426	0,75
	-0,837	-0,122	-0,533	-0,286	-0,112	0,426	0,75
	-0,837	0,533	-0,122	-0,286	-0,426	-0,112	0,75
	-0,837	-0,533	-0,122	-0,286	0,426	-0,112	0,75
[110]	-0,533	0,122	-0,837	-0,426	0,112	-0,286	30,3
[111]	0,533	0,122	-0,837	0,426	0,112	-0,286	44,2
[111]	-0,533	0,122	-0,837	-0,426	0,112	-0,286	37,1
[123]	0,122	-0,837	0,533	0,112	-0,286	-0,426	5,98
[123]	-0,533	-0,837	-0,122	0,426	-0,286	-0,112	6,33

Рис. 5. Полиэдрическая структура пакета мартенсита ( a , b , c ), микрофотография пакета [22] ( d ) и микрофотография зерна [108] ( e )

Fig. 5. Polyhedral structure of a martensite package ( a , b , c ), package microphotograph [22] ( d ) and grain microphotograph [108] ( e )

В разработанной модели существует возможность учитывать ориентации пластин мартенсита относительно аустенита и их отклонения от ориентационных соотношений Курдюмова – Закса. Учет взаимодействия пластин с окружением через плоские участки границ потенциально позволяет ввести в модель механизм деформации, реализующейся за счет смещения пластинок относительно друг друга, и механизм межфазной деформации между мартенситом и остаточным аустенитом. Введение таких геометрических характеристик, как объем и линейные размеры пластинок мартенсита, позволит учесть различную длину пробега дислокаций. В дальнейшем с использованием геометрического

Список литературы Многоуровневая модель описания мартенситного превращения: формирование полиэдрической структуры мартенсита

Heat treatment effect on mechanical properties of AISI 304 austenitic stainless steel / H. Essoussi, S. Elmouhri, S. Ettaqi, E. Es-sadiqi // Procedia Manufacturing. - 2019. - Vol. 32. - P. 883-888. DOI: 10.1016/j.promfg.2019.02.298
A review on machining performance of AISI 304 steel / A. Kumar, R. Sharma, S. Kumar, P. Verma // Materials Today: Proceedings. - 2022. - Vol. 56. - P. 2945-2951. DOI: 10.1016/j.matpr.2021.11.003
Mechanical Surface Treatments of AISI 304 Stainless Steel: Effects on Surface Microrelief, Residual Stress, and Microstructure / D.A. Lesyk, H. Soyama, B.N. Mordyuk, V.V. Dzhemelinskyi, S. Martinez, N.I. Khripta, A. Lamikiz // J. of Materi Eng and Perform. - 2019. - Vol. 28, no. 9. - P. 5307-5322. DOI: 10.1007/s11665-019-04273-y
Analysis of dependence of internal damping on temperature of austenitic steels AISI 304 and AISI 316L / M. Uhricik, M. Oravcova, P. Palcek, T. Orsulova, P. Hanusova // Transportation Research Procedia. - 2019. - Vol. 40. - P. 107-112. DOI: 10.1016/j.trpro.2019.07.018
Yang, G. An Overview of High Yield Strength Twinning-Induced Plasticity Steels: 1 / G. Yang, J.-K. Kim // Metals. - Multi-disciplinary Digital Publishing Institute, 2021. - Vol. 11, no. 1. -P. 124. DOI: 10.3390/met11010124
A polycrystal plasticity based discontinuous dynamic re-crystallization simulation method and its application to copper / G. Zhou, Z. Li, D. Li, Y. Peng, H.S. Zurob, P. Wu // International Journal of Plasticity. - 2017. - Vol. 91. - P. 48-76. DOI: 10.1016/j.ijplas.2017.01.001
Levitas, V.I. Thermomechanical theory of martensitic phase transformations in inelastic materials / V.I. Levitas // International Journal of Solids and Structures. - 1998. - Vol. 35, no. 9. - P. 889940. DOI: 10.1016/S0020-7683(97)00089-9
Zhao, J. Thermomechanical processing of advanced high strength steels / J. Zhao, Z. Jiang // Progress in Materials Science. - 2018. - Vol. 94. - P. 174-242. DOI: 10.1016/j.pmatsci.2018.01.006
Modelling martensitic transformation in titanium alloys: The influence of temperature and deformation / M. Bignon, E. Bertrand, F. Tancret, P.E.J. Rivera-Diaz-del-Castillo // Materialia. - 2019. - Vol. 7. - P. 100382. DOI: 10.1016/j.mtla.2019.100382
Crystallography and asymmetry of tensile and compres-sive stress-induced martensitic transformation in metastable в titanium alloy Ti-7Mo-3Nb-3Cr-3Al / P. Gao, J. Fan, F. Sun, J. Cheng, L. Li, B. Tang, H. Kou, J. Li // Journal of Alloys and Compounds. - 2019. - Vol. 809. - P. 151762. DOI: 10.1016/j.jall-com.2019.151762
The effect of quench rate on the ß-a" martensitic transformation in Ti-Nb alloys / E.L. Pang, E.M. Hildyard, L.D. Connor, E.J. Pickering, N.G. Jones // Materials Science and Engineering: A. -2021. - Vol. 817. - P. 141240. DOI: 10.1016/j.msea.2021.141240
The microstructure and martensitic transformation of Ti-V-Al-B elevated temperature shape memory alloy tailored by thermo-mechanical treatment / X. Yi, H. Wang, K. Sun, Y. Gong, X. Meng, H. Zhang, Z. Gao, W. Cai // Journal of Alloys and Compounds. - 2021. - Vol. 853. - P. 157059. DOI: 10.1016/j.jall-com.2020.157059
Effects of Parent Phase Aging and Nb Element on the Microstructure, Martensitic Transformation, and Damping Behaviors of a Cu-Al-Mn Shape Memory Alloy / H. Li, Q. Wang, F. Yin, C. Cui, G. Hao, Z. Jiao, N. Zheng // Physica Status Solidi (a). - 2020. -Vol. 217, № 6. - P. 1900923. DOI: 10.1002/pssa.201900923
Lu, N.-H. Inhomogeneous martensitic transformation behavior and elastocaloric effect in a bicrystal Cu-Al-Mn shape memory alloy / N.-H. Lu, C.-H. Chen // Materials Science and Engineering: A. -2021. - Vol. 800. - P. 140386. DOI: 10.1016/j.msea.2020.140386
Sequence of martensitic transformations in Ni-Mn-Ga alloys / V.A. Chernenko, C. Seguí, E. Cesari, J. Pons, V.V. Kokorin // Physical Review B. - 1998. - Vol. 57. - P. 2659-2662. DOI: 10.1103/PhysRevB.57.2659
Correlation between microstructure and martensitic transformation, mechanical properties and elastocaloric effect in Ni-Mn-based alloys / X.-M. Huang, L.-D. Wang, H.-X. Liu, H.-L. Yan, N. Jia, B. Yang, Z.-B. Li, Y.-D. Zhang, C. Esling, X. Zhao, L. Zuo // Intermetallics. - 2019. - Vol. 113. - P. 106579. DOI: 10.1016/j.in-termet.2019.106579
Duggin, M.J. Further studies of martensitic transformations in gold-copper-zinc and copper-aluminium-nickel alloys / M.J. Duggin // Acta Metallurgica. - 1966. - Vol. 14, no. 2. - P. 123129. DOI: 10.1016/0001-6160(66)90293-8
Enami, K. Crystal Structure and Internal Twins of the Ni-36.8 at% Al Martensite / K. Enami, S. Nenno, K. Shimizu // Transactions of the Japan Institute of Metals. - 1973. - Vol. 14, no. 2. -P. 161-165. DOI: 10.2320/matertrans1960.14.161
Jacobus, K. Effect of stress state on the stress-induced martensitic transformation in polycrystalline Ni-Ti alloy / K. Jacobus, H. Sehitoglu, M. Balzer // Metall Mater Trans A. - 1996. - Vol. 27, no. 10. - P. 3066-3073. DOI: 10.1007/BF02663855
Swann, P.R. The electron-metallography and crystallography of copper-aluminum martensites / P.R. Swann, H. Warlimont // Acta Metallurgica. - 1963. - Vol. 11, no. 6. - P. 511-527. DOI: 10.1016/0001-6160(63)90086-5
Albutt, K.J. The Metallography of Thermally Strengthened Low Carbon Steels / K.J. Albutt, D.E. Dalton, S. Garber; Gefügeuntersuchung von niedrigkohlenstofihaltigen Stählen nach thermischer Festigkeitserhöhung // Practical Metallography. - De Gruyter, 1968. -Vol. 5, no. 5. - P. 264-278. DOI: 10.1515/pm-1968-050503
Apple, C.A. Packet microstructure in Fe-0.2 pct C martensite / C.A. Apple, R.N. Caron, G. Krauss // Metall Trans. -1974. - Vol. 5, no. 3. - P. 593-599. DOI: 10.1007/BF02644654
Breedis, J.F. The formation of Hcp and Bcc phases in austenitic iron alloys / J.F. Breedis, L. Kaufman // Metall Mater Trans B. - 1971. - Vol. 2, no. 9. - P. 2359-2371. DOI: 10.1007/BF02814874
The mechanisms of y (fcc) ^ s (hcp) ^ a' (bcc) and direct y (fcc) ^ a' (bcc) martensitic transformation in a gradient austenitic stainless steel / Y. He, J. Gao, Y. He, K. Shin // J Mater Sci. - 2022. -Vol. 57, no. 8. - P. 5230-5240. DOI: 10.1007/s10853-022-06936-z
Evidence of FCC to HCP and BCC-martensitic transformations in a CoCrFeNiMn high-entropy alloy by severe plastic deformation / H. Shahmir, P. Asghari-Rad, M.S. Mehranpour, F. For-ghani, H.S. Kim, M. Nili-Ahmadabadi // Materials Science and Engineering: A. - 2021. - Vol. 807. - P. 140875. DOI: 10.1016/j.msea.2021.140875
Gundyrev, V.M. Crystallographic Analysis and Mechanism of Martensitic Transformation in Fe Alloys / V.M. Gundyrev, V.I. Zeldovich, V.M. Schastlivtsev // Phys. Metals Metallogr. -2020. - Vol. 121, no. 11. - P. 1045-1063. DOI: 10.1134/S0031918X20110046
Kurdjumov, G. Over the mechanisms of steel hardening / G. Kurdjumov, G. Sachs // Z. Phys. - 1930. - Vol. 64, no. 325-343.
Maki, T. Microstructure and Mechanical Behaviour of Ferrous Martensite / T. Maki // Materials Science Forum. - Trans Tech Publications Ltd, 1990. - Vol. 56-58. - P. 157-168. DOI: 10.4028/www.scientific.net/MSF.56-58.157
Influence of High-pressure Quenching on the Microstructure, Martensite Transformation, and Mechanical Properties of 0.2 Mass% C Steel / Q. Cui, J. Liu, C. Xu, Y. Xu, H. Huang, B. Wen, X. Lin // ISIJ Int. - The Iron and Steel Institute of Japan, 2021. -Vol. 61, no. 8. - P. 2292-2298. DOI: 10.2355/isijinternational.ISI-JINT-2020-784
Investigation of cold rolling variables on the formation of strain-induced martensite in 201L stainless steel / A. Rezaee, A. Kermanpur, A. Najafizadeh, M. Moallemi, H. Samaei Baghba-dorani // Materials & Design (1980-2015). - 2013. - Vol. 46. -P. 49-53. DOI: 10.1016/j.matdes.2012.09.054
Shamsolhodaei, A. Structural and functional properties of a semi equiatomic NiTi shape memory alloy processed by multiaxial forging / A. Shamsolhodaei, A. Zarei-Hanzaki, M. Moghad-dam // Materials Science and Engineering: A. - 2017. - Vol. 700. -P. 1-9. DOI: 10.1016/j.msea.2017.04.011
Quantitative analysis of the martensite transformation and microstructure characterization during cryogenic rolling of a 304 austenitic stainless steel / Shi J., Hou L., Zuo J., Lu L., Cui H., Zhang J. // Jinshu Xuebao/Acta Metallurgica Sinica. - 2016. -Vol. 52, no. 8. DOI: 10.11900/0412.1961.2015.00635
Towards the microstructure design of DP steels: A generic size-sensitive mean-field mechanical model / S.Y.P. Allain, O. Bouaziz, I. Pushkareva, C.P. Scott // Materials Science and Engineering: A. - 2015. - Vol. 637. - P. 222-234. DOI: 10.1016/j.msea.2015.04.017
McDowell, D.L. Microstructure-sensitive computational modeling of fatigue crack formation / D.L. McDowell, F.P.E. Dunne // International Journal of Fatigue. - 2010. - Vol. 32, no. 9. - P. 15211542. DOI: 10.1016/j.ijfatigue.2010.01.003
Avrami, M. Kinetics of Phase Change. II TransformationTime Relations for Random Distribution of Nuclei / M. Avrami // The Journal of Chemical Physics. - 1940. - Vol. 8, no. 2. - P. 212224. DOI: 10.1063/1.1750631
Hsu (Xu Zuyao), T.Y. Additivity hypothesis and effects of stress on phase transformations in steel / T.Y. Hsu (Xu Zuyao) // Current Opinion in Solid State and Materials Science. - 2005. DOI: 10.1016/j.cossms.2006.02.011
Inoue, T. Coupling between stress, temperature, and metallic structures during processes involving phase transformations / T. Inoue, Z. Wang // Materials Science and Technology. - Taylor & Francis, 1985. - Vol. 1, no. 10. - P. 845-850. DOI: 10.1179/mst.1985.1.10.845
Koistinen, D.P. A general equation prescribing the extent of the austenite-martensite transformation in pure iron-carbon alloys and plain carbon steels / D.P. Koistinen, R.E. Marburger // Acta Metallurgica. - 1959. DOI: 10.1016/0001-6160(59)90170-1
Trusov, P.V. Multilevel crystal plasticity models of single- and polycrystals. Direct models / P.V. Trusov, A.I. Shveykin // Phys Mesomech. - 2013. - Vol. 16, no. 2. - P. 99-124. DOI: 10.1134/S1029959913020021
Исупова, И.Л. Математическое моделирование фазовых превращений в сталях при термомаханической нагрузке / И.Л. Исупова, П.В. Трусов // Вестник пермского национального исследовательского политехнического университета. Механика. - 2013. - T. 3. - С. 127-157.
Пустовойт, В.Н. Исследование механизма образования зародышей мартенсита при закалке в магнитном поле / B.Н. Пустовойт, Ю.В. Долгачев // Упрочняющие технологии и покрытия. - 2007. - № 3. - С. 4-7.
Трусов, П. В. Многоуровневые модели моно-поликри-сталлических материалов: теория, алгоритмы, примеры применения / П.В. Трусов, А.И. Швейкин. - Изд-во СО РАН: Новосибирск, 2019. - 605 с.
Трусов, П.В. Многоуровневые физические модели монои поликристаллов. Статистические модели / П.В. Трусов, А.И. Швейкин // Физическая мезомеханика. - 2011. - № 4. - C. 17-28.
Tjahjanto, D.D. Crystallographically based model for transformation-induced plasticity in multiphase carbon steels / D.D. Tjahjanto, S. Turteltaub, A.S.J. Suiker // Continuum Mechanics and Thermodynamics. - Springer, 2008. - Vol. 19. - P. 399422. DOI: 10.1007/s00161-007-0061-x
Turteltaub, S. A multiscale thermomechanical model for cubic to tetragonal martensitic phase transformations / S. Turteltaub, A.S.J. Suiker // International Journal of Solids and Structures. - 2006. DOI: 10.1016/j.ijsolstr.2005.06.065
Исупова, И.Л. Двухуровневая модель для описания поведения сталей при термомеханическом нагружении с учетом мартенситных превращений: алгоритм реализации модели / И. Л. Исупова, П. В. Трусов // Вычислительная механика сплошных сред. - 2013. - Т. 6, № 4. - С. 491-503. DOI: 10.7242/1999-6691/2013.6.4.54
Guthikonda, V.S. Modeling martensitic phase transformations in shape memory alloys with the self-consistent lattice dynamics approach / V.S. Guthikonda, R.S. Elliott // Journal of the Mechanics and Physics of Solids. - 2013. - Vol. 61, no. 4. -P. 1010-1026. DOI: 10.1016/j.jmps.2012.12.003
A model for deformation behavior and mechanically induced martensitic transformation of metastable austenitic steel / H.N. Han, C.G. Lee, C.-S. Oh, T.-H. Lee, S.-J. Kim // Acta Materi-alia. - 2004. - Vol. 52, no. 17. - P. 5203-5214. DOI: 10.1016/j.ac-tamat.2004.07.031
Lu, Z.K. A self-consistent model for the stress-strain behavior of shape-memory alloy polycrystals / Z.K. Lu, G.J. Weng // Acta Materialia. - 1998. - Vol. 46, no. 15. - P. 5423-5433. DOI: 10.1016/S1359-6454(98)00203-1
Stringfellow, R.G. A self-consistent model of isotropic viscoplastic behavior in multiphase materials / R.G. Stringfellow, D.M. Parks // International Journal of Plasticity. - 1991. - Vol. 7, no. 6. - P. 529-547. DOI: 10.1016/0749-6419(91)90043-X
Kouznetsova, V.G. A multi-scale model of martensitic transformation plasticity / V.G. Kouznetsova, M.G.D. Geers // Mechanics of Materials. - 2008. DOI: 10.1016/j.mechmat.2008.02.004
Lee, M.-G. Crystal plasticity finite element modeling of mechanically induced martensitic transformation (MIMT) in meta-stable austenite / M.-G. Lee, S.-J. Kim, H.N. Han // International Journal of Plasticity. - 2010. - Vol. 26, no. 5. - P. 688-710. DOI: 10.1016/j.ijplas.2009.10.001
Trinh, T.D. A Crystal Plasticity Simulation on Strain-Induced Martensitic Transformation in Crystalline TRIP Steel by Coupling with Cellular Automata: 8 / T.D. Trinh, T. Iwamoto // Metals. - Multidisciplinary Digital Publishing Institute, 2021. -Vol. 11, no. 8. - P. 1316. DOI: 10.3390/met11081316
Overview of constitutive laws, kinematics, homogeniza-tion and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications / F. Roters, P. Eisenlohr, L. Hantcherli, D.D. Tjahjanto, T.R. Bieler, D. Raabe // Acta Materialia. - 2010. - Vol. 58, no. 4. - P. 1152-1211. DOI: 10.1016/j.ac-tamat.2009.10.058
Allain, S. Toward a New Interpretation of the Mechanical Behaviour of As-quenched Low Alloyed Martensitic Steels / S. Al-lain, O. Bouaziz, M. Takahashi // ISIJ International. - 2012. -Vol. 52, no. 4. - P. 717-722. DOI: 10.2355/isijinternational.52.717
Microstructural heterogeneity and its relationship to the strength of martensite / G. Badinier, C.W. Sinclair, X. Sauvage, X. Wang, V. Bylik, M. Goune, F. Danoix // Materials Science and Engineering: A. - 2015. - Vol. 638. - P. 329-339. DOI: 10.1016/j.msea.2015.04.088
Block and sub-block boundary strengthening in lath martensite / C. Du, J.P.M. Hoefnagels, R. Vaes, M.G.D. Geers // Scripta Materialia. - 2016. - Vol. 116. - P. 117-121. DOI: 10.1016/j.scrip-tamat.2016.01.043
The morphology and crystallography of lath martensite in alloy steels / S. Morito, X. Huang, T. Furuhara, T. Maki, N. Hansen // Acta Materialia. - 2006. - Vol. 54, no. 19. - P. 5323-5331. DOI: 10.1016/j.actamat.2006.07.009
Effect of block size on the strength of lath martensite in low carbon steels / S. Morito, H. Yoshida, T. Maki, X. Huang // Materials Science and Engineering: A. - 2006. - Vol. 438-440. -P. 237-240. DOI: 10.1016/j.msea.2005.12.048
3D structural and atomic-scale analysis of lath martensite: Effect of the transformation sequence / L. Morsdorf, C.C. Tasan, D. Ponge, D. Raabe // Acta Materialia. - 2015. - Vol. 95. - P. 366377. DOI: 10.1016/j.actamat.2015.05.023
Swarr, T. The effect of structure on the deformation of as-quenched and tempered martensite in an Fe-0.2 pct C alloy / T. Swarr, G. Krauss // Metall Trans A. - 1976. - Vol. 7, no. 1. -P. 41-48. DOI: 10.1007/BF02644037
Twin structure of the lath martensite in low carbon steel / P.Zhang, Y. Chen, W. Xiao, D. Ping, X. Zhao // Progress in Natural Science: Materials International. - 2016. - Vol. 26, no. 2. - P. 169172. DOI: 10.1016/j.pnsc.2016.03.004
Crystallographic features of lath martensite in low-carbon steel / H. Kitahara, R. Ueji, N. Tsuji, Y. Minamino // Acta Materialia. - 2006. - Vol. 54, no. 5. - P. 1279-1288. DOI: 10.1016/j.actamat.2005.11.001
Kohn, R.V. Surface energy and microstructure in coherent phase transitions / R.V. Kohn, S. Müller // Communications on Pure and Applied Mathematics. - 1994. - Vol. 47, no. 4. - P. 405-435. DOI: 10.1002/cpa.3160470402
Building hierarchical martensite / S. Schwabe, R. Niemann, A. Backen, D. Wolf, C. Damm, T. Walter, H. Seiner, O. Hec-zko, K. Nielsch, S. Fähler // Advanced Functional Materials. -Wiley Online Library, 2021. - Vol. 31, no. 7. - P. 2005715.
The Effect of Lath Martensite Micro structures on the Strength of Medium-Carbon Low-Alloy Steel: 3 / C. Sun, P. Fu, H. Liu, H. Liu, N. Du, Y. Cao // Crystals. - Multidisciplinary Digital Publishing Institute, 2020. - Vol. 10, no. 3. - P. 232. DOI: 10.3390/cryst10030232
Iwamoto, T. Finite Element Simulation of Martensitic Transformation in Single-Crystal TRIP Steel Based on Crystal Plasticity Theory with Cellular Automata Approach / T. Iwamoto, T. Tsuta // Key Engineering Materials. - Trans Tech Publications Ltd, 2004. - Vol. 274-276. - P. 679-684. DOI: 10.4028/www.sci-entific.net/KEM.274-276.679
Sun, F. Strain gradient crystal plasticity modelling of size effects in a hierarchical martensitic steel using the Voronoi tessellation method / F. Sun, E.D. Meade, N.P. O'Dowd // International Journal of Plasticity. - 2019. - Vol. 119. - P. 215-229. DOI: 10.1016/j.ijplas.2019.03.009
Zhi, Y. Simulation of Martensitic Transformation of High Strength and Elongation Steel by Cellular Automaton / Y. Zhi, W.J. Liu, X. Liu // Advanced Materials Research. - Trans Tech Publications Ltd, 2014. - Vol. 1004-1005. - P. 235-238. DOI: 10.4028/www.scientific.net/AMR.1004-1005.235
Ozsoy, I.B. Finite element simulations of microstructure evolution in stress-induced martensitic transformations / I.B. Ozsoy, N. Babacan // International Journal of Solids and Structures. -2016. - Vol. 81. - P. 361-372. DOI: 10.1016/j.ijsolstr.2015.12.009
Phase-field modeling of multivariant martensitic transformation at finite-strain: Computational aspects and large-scale finite-element simulations / K. Tüma, M. Rezaee-Hajidehi, J. Hron, P.E. Farrell, S. Stupkiewicz // Computer Methods in Applied Mechanics and Engineering. - 2021. - Vol. 377. - P. 113705. DOI: 10.1016/j.cma.2021.113705
Three-dimensional phase-field modeling of martensitic microstructure evolution in steels / H.K. Yeddu, A. Malik, J. Agren, G. Amberg, A. Borgenstam // Acta Materialia. - 2012. - Vol. 60, no. 4. - P. 1538-1547. DOI: 10.1016/j.actamat.2011.11.039
Krauss, G. The morphology of martensite in iron alloys / G. Krauss, A.R. Marder // Metallurgical Transactions. - 1971. DOI: 10.1007/BF02814873
Farias, F. On the strain-induced martensitic transformation process of the commercial AISI 304 stainless steel during cyclic loading / F. Farias, I. Alvarez-Armas, A.F. Armas // International Journal of Fatigue. - Elsevier, 2020. - Vol. 140. - P. 105809.
High Strain Rate and Stress-State-Dependent Martensite Transformation in AISI 304 at Low Temperatures / L.V. Fricke, G. Gerstein, A. Kotzbauer, B. Breidenstein, S. Barton, H.J. Maier // Metals. - MDPI, 2022. - Vol. 12, no. 5. - P. 747.
Cech, R.E. Heterogeneous Nucleation of the Martensite Transformation / R.E. Cech, D. Turnbull // JOM. - 1956. - Vol. 8, no. 2. - P. 124-132. DOI: 10.1007/BF03377656
Levitas, V.I. Continuum modeling of strain-induced mar-tensitic transformation at shear-band intersections / V.I. Levitas, A.V. Idesman, G.B. Olson // Acta Materialia. - 1998. - Vol. 47, no. 1. - P. 219-233. DOI: 10.1016/S1359-6454(98)00314-0
Olson, G.B. Stress-assisted isothermal martensitic transformation: application to TRIP steels / G.B. Olson, M. Cohen // Metallurgical Transactions A. - Springer, 1982. - Vol. 13. -P. 1907-1914.
Easterling, K.E. The nucleation of martensite in steel / K.E. Easterling, A.R. Thôlén // Acta Metallurgica. - 1976. -Vol. 24, no. 4. - P. 333-341. DOI: 10.1016/0001-6160(76)90008-0
Micromechanics and microstructure evolution during in situ uniaxial tensile loading of TRIP-assisted duplex stainless steels / Y. Tian, S. Lin, J.Y.P. Ko, U. Lienert, A. Borgenstam, P. Hedström // Materials Science and Engineering: A. - 2018. - Vol. 734. - P. 281290. DOI: 10.1016/j.msea.2018.07.040
Olson, G.B. A general mechanism of martensitic nucleation: Part I. General concepts and the FCC ^ HCP transformation / G.B. Olson, M. Cohen // Metall Mater Trans A. - 1976. - Vol. 7, no. 12. - P. 1897-1904. DOI: 10.1007/BF02659822
Olson G.B., Cohen M. A general mechanism of martensitic nucleation: Part II. FCC ^ BCC and other martensitic transformations // Metall Mater Trans A. - 1976. - Vol. 7, no. 12. -P. 1905-1914. DOI: 10.1007/BF02659823
Olson, G.B. A general mechanism of martensitic nucleation: Part III. Kinetics of martensitic nucleation / G.B. Olson, M. Cohen // Metall Mater Trans A. - 1976. - Vol. 7, № 12. -P. 1915-1923. DOI: 10.1007/BF02659824
Lecroisey, F. Martensitic transformations induced by plastic deformation in the Fe-Ni-Cr-C system / F. Lecroisey, A. Pineau // Metallurgical Transactions. - 1972. DOI: 10.1007/BF02642042
Characteristics of nucleation and transformation sequence in deformation-induced martensitic transformation / J.L. Wang, M.H. Huang, X.H. Xi, C.C. Wang, W. Xu // Materials Characterization. - 2020. - Vol. 163. - P. 110234. DOI: 10.1016/j.matchar.2020.110234
The microstructure of lath martensite in quenched 9Ni steel / C.C. Kinney, K.R. Pytlewski, A.G. Khachaturyan, J.W. Morris // Acta Materialia. - 2014. - Vol. 69. - P. 372-385. DOI: 10.1016/j.actamat.2014.01.058
Mukherjee, K. Thermal effects associated with stress-induced martensitic transformation in a Ti-Ni alloy / K. Mukherjee, S. Sircar, N.B. Dahotre // Materials Science and Engineering. - 1985. -Vol. 74, no. 1. - P. 75-84. DOI: 10.1016/0025-5416(85)90111-9
Trusov, P.V. On motion decomposition and constitutive relations in geometrically nonlinear elastoviscoplasticity of crystallites / P.V. Trusov, A.I. Shveykin // Phys Mesomech. - 2017. -Vol. 20, no. 4. - P. 377-391. DOI: 10.1134/S1029959917040026
Трусов, П.В. О разложении движения, независимых от выбора системы отсчета производных и определяющих соотношениях при больших градиентах перемещений: взгляд с позиций многоуровневого моделирования: 2 / П.В. Трусов, А.И. Швейкин, А.Ю. Янц // Физическая мезомеханика. - Россия, Томск: Федеральное государственное бюджетное учреждение науки «Институт физики прочности и материаловедения Сибирского отделения Российской академии наук», 2016. -Т. 19, № 2. - С. 49-65.
Anand, L. Single-crystal elasto-viscoplasticity: application to texture evolution in polycrystalline metals at large strains / L. Anand // Computer methods in applied mechanics and engineering. - Elsevier, 2004. - Vol. 193, no. 48-51. - P. 5359-5383.
Bronkhorst, C.A. Polycrystalline plasticity and the evolution of crystallographic texture in FCC metals / C.A. Bronkhorst, S.R. Kalidindi, L. Anand // Philosophical Transactions of the Royal Society of London. Series A: Physical and Engineering Sciences. - Royal Society, 1992. - Vol. 341, no. 1662. - P. 443-477. DOI: 10.1098/rsta.1992.0111
Dislocation activities at the martensite phase transformation interface in metastable austenitic stainless steel: An in-situ TEM study / J. Liu, C. Chen, Q. Feng, X. Fang, H. Wang, F. Liu, J. Lu, D. Raabe // Materials Science and Engineering: A. - 2017. -Vol. 703. - P. 236-243. DOI: 10.1016/j.msea.2017.06.107
Dislocation-grain boundary interactions in martensitic steel observed through in situ nanoindentation in a transmission electron microscope / T. Ohmura, A.M. Minor, E.A. Stach, J.W. Morris // Journal of Materials Research. - Cambridge University Press, 2004. - Vol. 19, no. 12. - P. 3626-3632. DOI: 10.1557/JMR.2004.0474
Pan, H. Interactions between Dislocations and Boundaries during Deformation: 4 / H. Pan, Y. He, X. Zhang // Materials. -Multidisciplinary Digital Publishing Institute, 2021. - Vol. 14, no. 4. - P. 1012. DOI: 10.3390/ma14041012
Effect of quenching temperature on martensite multi-level microstructures and properties of strength and toughness in 20CrNi2Mo steel / S. Long, Y. Liang, Y. Jiang, Y. Liang, M. Yang, Y. Yi // Materials Science and Engineering: A. - 2016. -Vol. 676. - P. 38-47. DOI: 10.1016/j.msea.2016.08.065
Няшина, Н. Моделирование мартенситных превращений в сталях: кинематика мезоуровня / Н. Няшина, П. Трусов // Вестник Пермского национального исследовательского политехнического университета. Механика. - 2014. - № 4. - С. 118-151.
Coleman, B.D. The Thermodynamics of Elastic Materials with Heat Conduction and Viscosity / B.D. Coleman, W. Noll // The Foundations of Mechanics and Thermodynamics: Selected Papers / ed. Noll W. - Berlin, Heidelberg: Springer, 1974. - P. 145-156. DOI: 10.1007/978-3-642-65817-4_9
Galindo-Nava, E.I. A model for the microstructure behaviour and strength evolution in lath martensite / E.I. Galindo-Nava, P.E.J. Rivera-Diaz-del-Castillo // Acta Materialia. - 2015. -Vol. 98. - P. 81-93. DOI: 10.1016/j.actamat.2015.07.018
Quey, R. Large-scale 3D random polycrystals for the finite element method: Generation, meshing and remeshing / R. Quey, P.R. Dawson, F. Barbe // Computer Methods in Applied Mechanics and Engineering. - 2011. - Vol. 200, no. 17. - P. 17291745. DOI: 10.1016/j.cma.2011.01.002
Quey, R. Optimal polyhedral description of 3D poly-crystals: Method and application to statistical and synchrotron X-ray diffraction data / R. Quey, L. Renversade // Computer Methods in Applied Mechanics and Engineering. - 2018. - Vol. 330. -P. 308-333. DOI: 10.1016/j.cma.2017.10.029
Effects of strain rate on strain-induced martensite nucleation and growth in 301LN metastable austenitic steel / L. Pun, G.C. Soares, M. Isakov, M. Hokka // Materials Science and Engineering: A. - 2022. - Vol. 831. - P. 142218. DOI: 10.1016/j.msea.2021.142218
Pereira, A. de M. Effects of Strain-Rate and Deformation Mode on Strain-Induced Martensite Transformation of AISI 304L Steel Sheet / M. Pereira A. de, M.C. Cardoso, L.P. Moreira // Applied Mechanics and Materials. - Trans Tech Publications Ltd, 2016. -Vol. 835. - P. 216-221. DOI: 10.4028/www.scientific.net/AMM.835.216
Li, Y. Fatigue crack initiation (in 304L steel): influence of the microstructure and variable amplitude loading / Y. Li. - Ecole Centrale Paris, 2012.
Strain Hardening of a Layered and Nanostructured AISI 304 Stainless Steel / Y. Jia, Y. Liang, A. Chen, D. Pan // J. Iron Steel Res. Int. - 2014. - Vol. 21, no. 4. - P. 439-443. DOI: 10.1016/S1006-706X(14)60068-6
Naghizadeh, M. Effects of Grain Size on Mechanical Properties and Work-Hardening Behavior of AISI 304 Austenitic Stainless Steel / M. Naghizadeh, H. Mirzadeh // steel research international. -2019. - Vol. 90, no. 10. - P. 1900153. DOI: 10.1002/srin.201900153
Rodríguez-Martínez, J. A. Experimental study on the martensitic transformation in AISI 304 steel sheets subjected to tension under wide ranges of strain rate at room temperature / J.A. Rodríguez-Martínez, R. Pesci, A. Rusinek // Materials Science and Engineering: A. - 2011. - Vol. 528, no. 18. - P. 5974-5982. DOI: 10.1016/j.msea.2011.04.030
Twinning and martensite in a 304 austenitic stainless steel / Y.F. Shen, X.X. Li, X. Sun, Y.D. Wang, L. Zuo // Materials Science and Engineering: A. - 2012. - Vol. 552. - P. 514-522. DOI: 10.1016/j.msea.2012.05.080
Naraghi, R. Martensitic Transformation in Austenitic Stainless Steels / R. Naraghi. - 2009.

Еще

Статья научная