Многоуровневая расчетно-экспериментальная система для анализа прочности и жесткости элементов конструкций из короткоармированных композитов

Внедрение перспективных композиционных материалов позволяет повысить весовую эффективность конструкций [1]. Актуальность использования короткоармированных композиционных материалов обусловлена тем, что слоистые композиты не могут быть использованы в узлах навески, подверженным сложным пространственным нагружениям вследствие низкой прочности при их расслоении. Тер-

мопластичные композиционные материалы, армированные короткими высокопрочными волокнами, обладают высокими удельными характеристиками (прочность, жесткость), технологичностью, стойкостью к воздействию агрессивных сред, высокой ударной вязкостью. Однако, высокая зависимость характеристик материала от параметров литья изделий повышает требования к используемым при проектировании моделям и контролю постоянства разработанной технологии производства [2]. Исследование механических характеристик ко-роткоармированных композитов проведено на основе полиэфирэфиркетона, армированного короткими угольными волокнами с содержанием 20% (PEEK 90HMF20) [3].

Используемый материал хорошо зарекомендовал себя в авиационной и космической промышленности [4, 5] ввиду своих высоких механических характеристик, а также весовой эффективности. Жесткость и прочность корот-коармированного материала зависит от ориен- тации волокон в изделии. Управление течением расплава позволяет влиять на расположение волокон в таких материалах [6]. Сравнение данных, получаемых в программных комплексах, моделирующих литье, с экспериментальными данными показывают хорошую сходимость [7]. Для подробной оценки напряженно-деформированного состояния сложных изделий используется многоуровневых подход [8].

В качестве объекта исследования в статье рассмотрены проушины, поскольку они содержат концентраторы напряжений и являются типовыми элементами аэрокосмических конструкций. В статье [9] разработана методика оценки соответствия расчётных и экспериментальных значений разрушающих нагрузок для образцов регулярных и нерегулярных зон конструкций из слоистых композитов на примере проушин. Представленная далее работа посвящена развитию данной методики – распространению ее на случай композиционных материалов, армированных короткими высокопрочными волокнами.

Целью работы является определение путей настройки теоретической модели и экспериментальных методик для повышения точности моделирования структуры повышаемого материала. Для решения этих задач применен многоуровневый подход, реализованный в совместном использовании программных комплексов Moldex3D, DIGIMAT и ANSYS. Схема многоуровневого подхода представлена на рис. 1.

Для предсказания прочности конструкции использовались критерии эквивалентных напряжений, а также критерий Цая-Хилла для трансверсально-изотропных тел (3D), с использованием постановки первого разрушенного псевдо-зерна FPGF fi = V F И, (1)

где

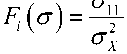
^G 11^{( G} 22 + ^ 33^ ■ ^ 22 + ^ 33 ■

2       +         +

^ Х         ^ У

^{1     2}            ^ 12 + ^ 13

⁺ (—-- 2 ^ 22 ^ 33 ^{+ 12} 2 ¹³

^ Х   ^ У           ^ S

+ (— - Т ^ и, (2)

^ У   ^ х

°"₁₁ ... ^ ₁₃ - компоненты тензора напряжений в главных осях,

^X - предел прочности при растяжении в направлении армирования, сУ - предел прочности в трансверсальном направлении,

^ _S - предел прочности при сдвиге.

Постановка FPGF (рис. 2) предполагает использование модели первого разрушенного псевдо-зерна для армированных пластиков [10]. Конечно-элементная модель изделия разделяется на ячейки представительного объема (элементы сетки), которые в свою очередь делятся на псевдо-зерна. При расчете полностью разрушенное зерно исключается. Наступление разрушения всей ячейки периодичности определяется массовой долей разрушенных псевдо-зерен PGA, которая рассчитываются по формуле:

PGA =

:е ®kFk k=1

^PGAcritical ^,

где N – общее число псевдо-зерен;

to _k - вес одного псевдо-зерна, который отражает ориентацию волокна;

F_k – значение метки, которое равно 0 при целом псевдо-зерне и 1, если зерно разрушено;

PGA_critical – критическое значение массовой доли разрушенных псевдо-зерен.

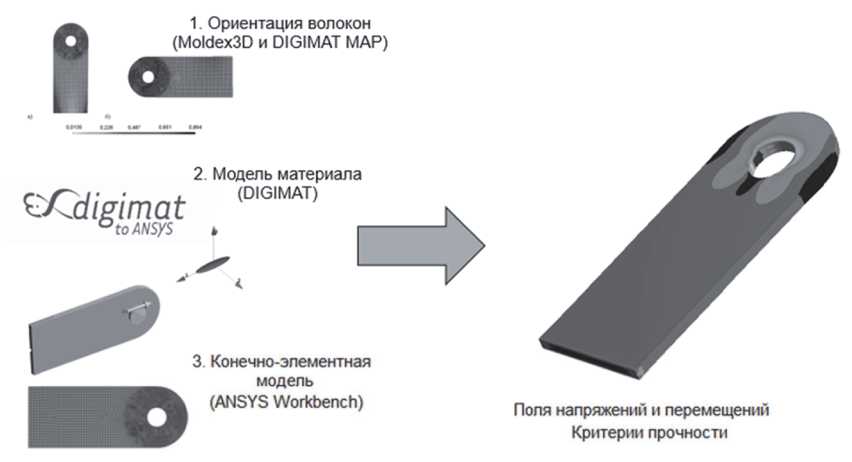
Риc. 1. Схема многоуровневого подхода

Ячейка

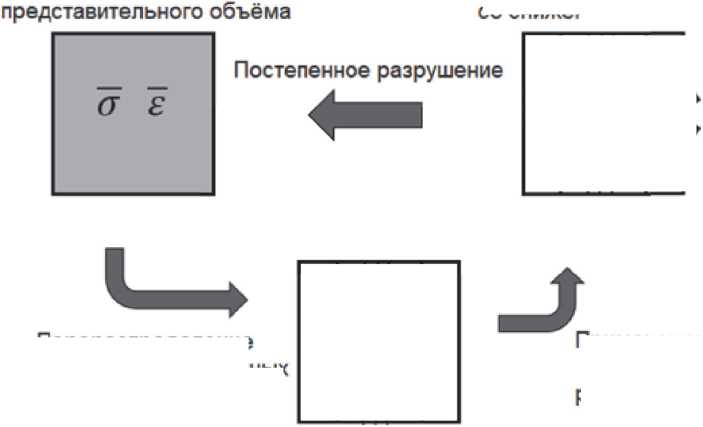
Применение критерия разрушения

Риc. 2. Схема концепции FPGF

Ячейка представительного объёма со сниженной жесткостью

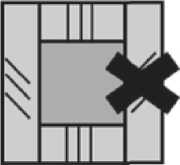
Перераспределение жесткостных и прочностных характеристик

2.    МОДЕЛИРОВАНИЕ ЛИТЬЯ ПЛАСТИНЫ И РАСЧЕТ ОРИЕНТАЦИИ ВОЛОКОН

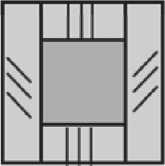
Для определения ориентации волокон внутри пластины проводилось моделирование её литья в системе Moldex 3D. Моделирование позволяет сократить многочисленные итерации по подбору технологического режима и сократить срок изготовления продукции. Размеры пластины выбраны с учетом возможности расположения проушин двух размеров в разных направлениях. На рис. 3 представлены размеры изготавливаемой пластины и проушин.

Сетка пластины построена в Rhinoceros – программе, позволяющей создавать сложные

Рис. 3. Размеры изготавливаемой пластины и проушин двух размеров структурированные сетки и назначать атрибуты граничных условий литья: место входа расплава, определять литниковую систему и полость для заполнения расплавом. Сетка имеет 20 слоев с ячейками размером 0,5x0,2 мм. Расчетная сетка пластины в различных областях представлена на рис. 4.

Параметры неньютоновского материала PEEK 90HMF20 построены по аналогии с имеющимся в базе данных Moldex 3D PEEK 90HMF40, с учётом поправок, определяемых разницей значениях их ключевых характеристик, определяемых спецификациями [3] и [11]. Технологические параметры процесса литья [12] заданы в системе Moldex 3D на основе спецификации используемого для литья термопласт автомата Negri Bossi VE 210-1700 (табл. 1).

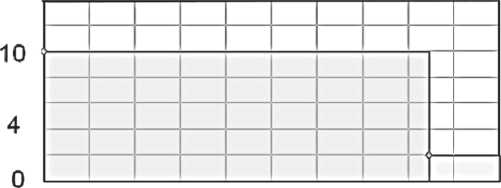
При моделировании литья конструкций под давлением задан ступенчатый профиль изменения объемной скорости впрыска расплава в зависимости от позиции поршня литьевой машины (рис. 5) соответствующий процессу литья

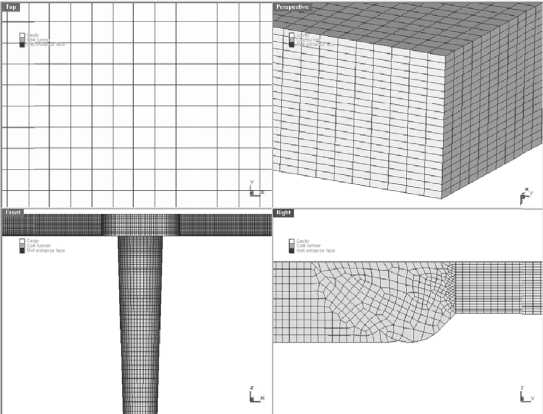
Рис. 4. Конечно-элементная модель пластины в различных областях

Таблица 1. Основные параметры технологического процесса литья

Параметр	Значение
Диаметр шнека, мм	60
Скорость вращения шнека, об/мин	25
Инжекционное давление, МПа	150
Сила зажима, тс	210

Скорость впрыска, мм/с

65    52     39     26     13      0 поршня, мм

Рис. 5. Ступенчатый профиль изменения объемной скорости впрыска расплава в зависимости от позиции поршня литьевой машины

пластин, изготовленных для эксперимента. Расплав подается в форму со скоростью впрыска 10 мм/с, температура формы составляет 220 °С, а температура расплава – 400 °С.

Результатом расчета является поля распространения фронта литья, давлений и температур, а также значений компонент тензора ориентации армирующих волокон в каждой точке изделия. Расчет показал полное заполнение литьевой формы, время литья составило 5,2 с. На рис. 6 показаны фронты литья пластины в зависимости от времени.

Для сравнения полученной картина вероятностного распределения волокон в пластине материала с проведенным моделированием было проведено исследование среза проушин на электронном микроскопе TESCAN VEGA. На рис. 7 видно, что в структуре проушин S90 при литье образуется ярко выраженный средний слой волокон, которые направлены хаотично. Для проушин S0 волокна в ядре ориентированы по направлению литья (рис. 8).

Ориентация волокон, полученная в Moldex 3D, с помощью модуля Digimat MAP, сохранена для каждой проушины в месте ее вырезки для построения многоуровневой математической модели изделия.

3.    СОЗДАНИЕ МНОГОУРОВНЕВОЙ МОДЕЛИ МАТЕРИАЛА

В статье рассмотрен анизотропный материал PEEK 90HMF20. Для более точного учета поведения материала при прочностном расчете, а также прогнозирования прочности проектируемого изделия, необходимо создать модель на основе результатов испытаний, а также паспортных характеристик материала. Построе- ние модели материала выполнено в программном комплексе Digimat, в котором возможно аналитическое прогнозирование нелинейного поведения материалов.

В модуле Digimat-MF создана модель материала, исходя из паспортных характеристик

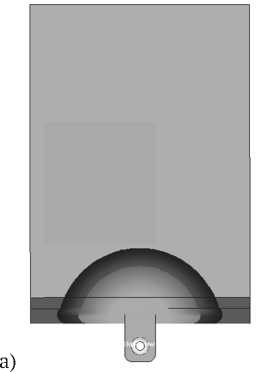
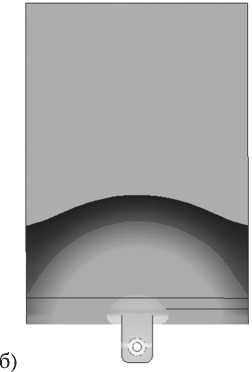
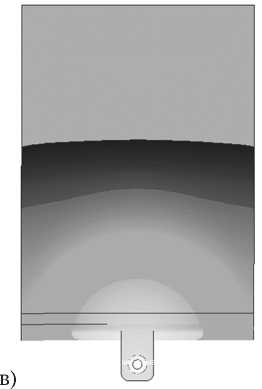
Рис. 6. Фронты литья пластины из PEEK 90HMF20: а) на 1 секунде, б) на 2 секунде, в) на 3 секунде, г) на 5 секунде

Рис. 7. Направление волокон в торце проушин S₉₀: а) электронный микроскоп TESCAN VEGA, б) Moldex 3D

Рис. 8. Направление волокон в торце проушин S₀: а) электронный микроскоп TESCAN VEGA, б) Moldex 3D

каждого компонента. Прочностные свойства компонентов, а также композита в целом описываются с помощью критерия Цая-Хилла для трансверсально-изотропных тел (3D). Критерий позволяет достоверно предсказывать разрушение конструкции при минимуме необходимых экспериментальных исследований, так как требуется определение только трех предельных параметров: пределы прочности при растяжении в направлении армирования (X) и в трансверсальном направлении (Y), а также предел прочности при сдвиге (S).

Модель материала строится на результате на основе результатов испытаний плоских образцов по стандарту ISO 527, вырезанных под различным углом относительно направления литья (рис. 9). Средние значений механических характеристик образов и коэффициенты вариации представлены в табл. 2.

Полученный файл анализа материала передается в модуль Digimat-MX, в котором проходит реверс-инжинирингг – итерационный процесс поиска оптимальных проектировочных переменных, определяющих константы выбранного закона деформирования материала. Данный подход используется для сокращения разницы между аналитической моделью Digimat-MF и данными, получаемыми в результате эксперимента и добавляемыми в базу Digimat-MX в качестве тестового файла, содержащего значения напряжений и деформаций. Результаты реверс-инжиниринга представлен на рисунке (рис. 10).

Результатом работы с программным комплексом DIGIMAT является модель материала, содержащая оптимизированные свойства компонентов композита. Параметры модели связующего были скорректированы в ходе реверс-инжиниринга таким образом, чтобы свойства

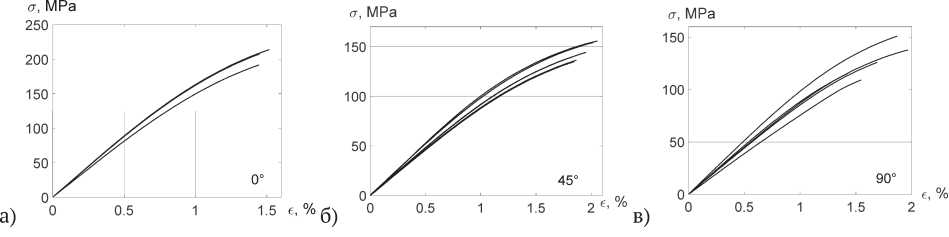
Рис. 9. Результаты испытаний плоских образцов:

а) 0°, б) 45°, в) 90°

Таблица 2. Механические характеристики плоских образцов

Расположение образца на пластине E, МПа CVE, % ^тах , МПа CV , тах % 0° 17381 3,7 205 4,2 45° 9765 5,6 144 6,2 90° 9040 9,9 128 13,2 engineering strain vs engineering stress

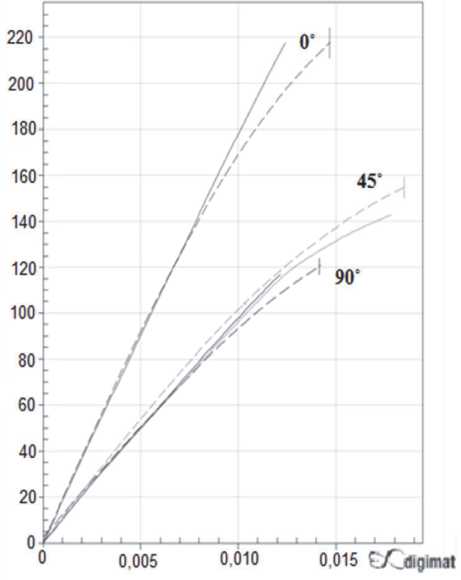
Рис. 10. Реверс-инжиниринг в модуле Digimat-MX композита в целом соответствовали экспериментально полученным зависимостям напряжений от деформаций для образов вырезных под углом 0°, 45° и 90° к направляющей пластины. Результаты реверс-инжиниринга представлены в табл. 3 – 5.

Построенная модель материала использована при расчёте напряженно-деформированного проушин из материала PEEK 90HMF20 и позволяет учитывать зависимость его механических характеристик от направления армирования.

Таблица 3. Параметры волокна по результатам реверс-инжиниринга

Параметр	Значение
Модуль Юнга, МПа	42000
Коэффициент Пуассона	0,2
Плотность, кг/м3	1565

Таблица 4. Параметры связующего по результатам реверс-инжиниринга

Параметр	Значение
Модуль Юнга, МПа	5994
Коэффициент Пуассона	0,4559
Предел текучести, МПа	20
Плотность, кг/м3	1300
Константа упрочнения	211
Экспонента при законе упрочнения	0,17

Таблица 5. Параметры критерия разрушения по результатам реверс-инжиниринга

Предел прочности при растяжении в направлении армирования G X , МПа	225
Предел прочности при растяжении в поперечном направлении G Y , МПа	110
Предел прочности при сдвиге G S , МПа	85

4.    ЭКСПЕРИМЕНТАЛЬНАЯ ОЦЕНКА ХАРАКТЕРИСТИК ПРОУШИН

Проушины вырезаны из пластин методом гидроабразивной резки. Боковая поверхность проушин отшлифована. Отверстие проушин получено сверлением и разверткой. Проушины испытаны на растяжение с плавным возрастанием нагрузки вплоть до момента разрушения на универсальной сервогидравлической машине MTS 793. Испытания проведены по схеме, предложенной Комаровым В.А. [9]. В табл. 6 представлено номинальное напряжение в отверстии F

σ =     , где F – разрушающее усилия, Н, d –

H d • h диаметр отверстия проушины, мм, h – толщина проушины, мм.

• 5.    РАСЧЕТ

НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ПРОУШИН

Многоуровневый подход включает в себя конечно-элементную модель изделия. В мо- дуль DesignModeler системы ANSYS подгружалась 3D-модель пластины, а также создавалась геометрическая модель оси, с помощью которой задавалось нагружение. Схема закрепления проушины представлена на рис. 11. Конечно-элементная модель проушины М с осью содержит 40980 конечных элемента и 180694 узла.

В расчете задавался ряд значений перемещения оси для каждого размера проушин. Для каждого значения перемещения определялась сила растяжения проушины, поля эквивалентных напряжений и деформаций, а также критерии разрушения.

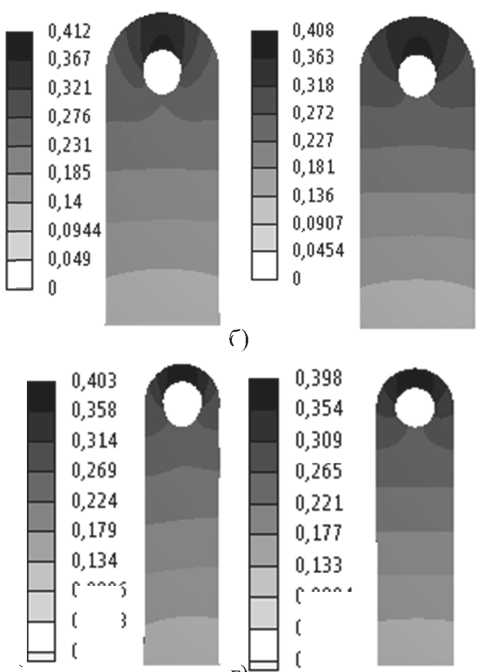
Разрушающее усилие (таблица 7) соответствует толщине рассчитываемых в ANSYS проушин 3,7 мм и значению экспериментально полученных номинальных напряжений (таблица 6). На рис. 12 - 14, представлены поля перемещений, эквивалентных напряжений по Мизесу и критерия Цая-Хилла для трансверсально-изотропных тел (3D) в постановке FPGF для исследованных типов проушин, нагруженных разрушающим усилием (таблица 7).

Таблица 6. Номинальное напряжение в проушинах О _н , МПа

N эксперимента	M 0	M 90	S 0	S 90
1	136,6	110,1	88,3	64,7
2	137,4	96,9	86,8	70,3
3	141,0	100,9	86,7	63,8
4	128,0	114,4	86,8	73,9
Среднее значение	135,8	105,6	87,2	68,2
CV, %	4%	8%	1%	7%

Таблица 7. Разрушающее усилие для проушин толщиной 3,7 мм

Типоразмер проушины	M 0	M 90	S 0	S 90
Разрушающее усилие, Н	6027,3	4687,9	3870,2	3026,6

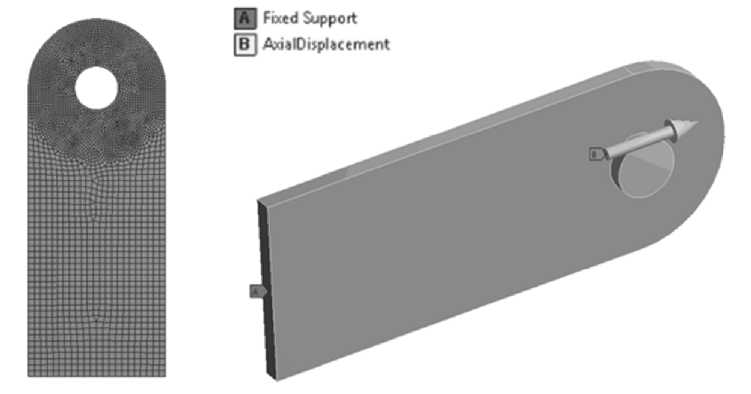
Рис. 11. Конечно-элементная модель проушины и схема закрепления

а)

б)

в ⁾

0,0896 0,0448

0,0884 0,0442 О

6.    ПРЕДСКАЗАНИЕ РАЗРУШАЮЩЕГО УСИЛИЯ

В табл. 8 приведено сравнение значений разрушающего усилия, полученных экспериментально и прогнозируемого по критериям Цая-Хилла и Мизеса в напряжениях с использованием анизотропной и изотропной моделях материалов для проушин толщиной 3,7 мм. Значение разрушающего усилия по критерию Цая-Хилла для трансверсально-изотропных тел (3D) в постановке FPGF получено на основе многоуровневого подхода с учетом ориентации армирующих волокон и параметров материала, представленных в таблицах 3 - 5 и соответствует минимальному усилию, когда значение критерия достигает единицы. Разрушающее усилие по критерию Мизеса соответствует значению усилия при которых максимальное значение эквивалентных напряжений по Мизесу, рассчитанных для изотопного материала (E = 17381 МПа), равно пределу прочности плоских образцов (таблица 2) в соответствии с направлением прилагаемой нагрузки: σ _m ⁰ _ax = 205 МПа для проушин S₀ и M₀ и σ _m ⁹⁰ _ax = 128 МПа для проушин S₉₀ и M₉₀.

в )

б)

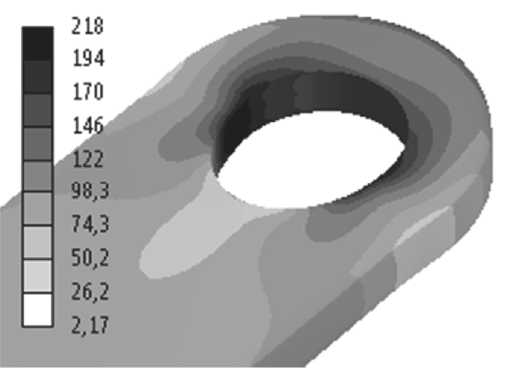
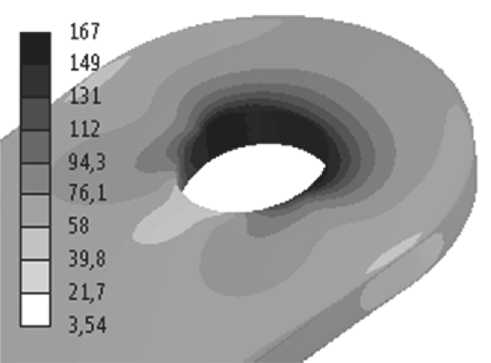
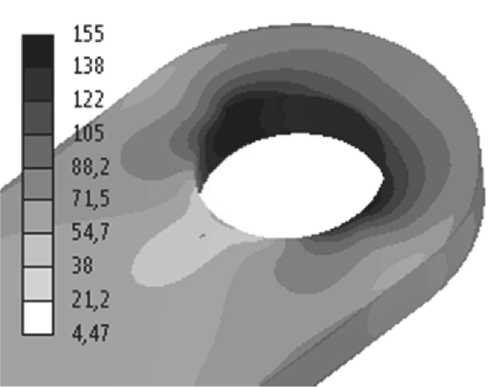
Рис. 13. Поля эквивалентных напряжений по Мизесу, МПа: а) M₀, б) M₉₀, в) S₀, г) S₉₀

Рис. 12. Поля перемещений проушин, мм: а) M₀, б) M₉₀, в) S₀, г) S₉₀

a)

в)

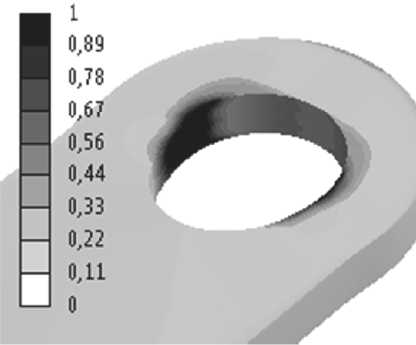
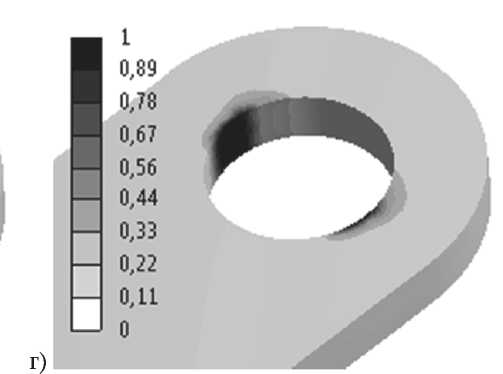
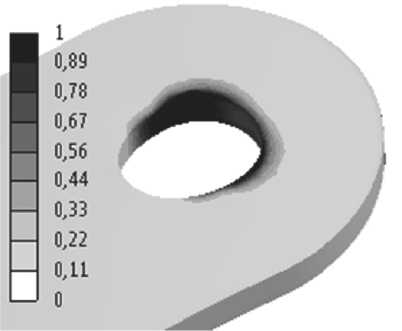
Рис. 14. Значение критерия Цая-Хилла в постановке FPGF: а) M₀, б) M₉₀, в) S₀, г) S₉₀

Таблица 8. Предсказание разрушающего усилия по критериям Цая-Хилла в постановке FPGF и Мизеса

Вид проушины	Разрушающее усилие, Н			Отношение предсказанного разрушающего усилия к эксприментальному
	Эксперимент	Цая-Хилл FPGF	Мизес	Цая-Хилл/ Эксперимент	Мизес / Эксперимент
M 0	6027	5521	5374	0,916	0,892
M 90	4688	4334	3346	0,924	0,714
S 0	3870	3628	3507	0,937	0,906
S 90	3027	2857	2189	0,944	0,723

7.    ВЫВОДЫ

Разработана многуровневая расчетно-экспериментальная система для анализа прочности и жесткости элементов конструкций из короткоармированных композитов, объединяющая модели ориентации армирующих волокон (Moldex3D), механических характеристик анизотропного материала (Digimat), конечно-элементную модель изделия (ANSYS Workbench). Экспериментальное подтверждение системы представлено на основе ис- следования жесткости и прочности образцов проушин из короткоармированного композиционного материала PEEK 90HMF20 двух типоразмеров, вырезанных из пластины вдоль и поперек направления литья. Показано, что критерий Цая-Хилла для трансверсальноизотропных тел (3D), с использованием постановки первого разрушенного псевдо-зерна FPGF позволяет достоверно предсказывать несущую способность конструкций изготавливаемых литьем из короткоармированных материалов.