Многоуровневые модели пластичности многофазных поликристаллических материалов, основанные на физических теориях пластичности и вязкопластичности

PNRPU MECHANICS BULLETIN

Начиная с конца прошлого века в континуальной механике наряду с развитием мак-рофеноменологических подходов к описанию упругопластического деформирования твердого тела продолжаются попытки, и часто весьма успешные, по созданию теорий, основанных на рассмотрении реальных физических механизмов деформирования, присущих достаточно широкому классу тел. Под физическими теориями пластичности (ФТП), следуя работам [1, 8, 12], будем понимать «широкий класс теорий пластичности, в основе формулировок определяющих соотношений, гипотез и основных положений которых лежит рассмотрение в явной форме механизмов деформирования на мезо- и микромасштабах (т.е. масштабных уровнях, меньших уровня представительного объема в макросмысле или представительного объема в инженерном смысле)». Отдельно стоит отметить работы, которые являются основополагающими в физических теориях пластичности как отдельного класса моделей неупругости. Это работы Дж.И. Тейлора, К.Ф. Элам [61–63] и Г.О. Закса [46, 51]. Согласно предложенному в этих работах подходу в дальнейшем появилось огромное количество модификаций физических теорий, в большинстве которых имеются признаки теорий отмеченных авторов, в особенности Дж.И. Тейлора.

Физические теории получили распространение для описания широкого класса материалов, в особенности поликристаллических. Обзор физических теорий пластичности, используемых для описания преимущественно однофазных поликристаллических материалов, можно найти в работах [4–6]. В последние десятилетия значительный интерес с точки зрения математического моделирования упругопластического поведения привле- кают многофазные поликристаллические материалы, получившие широкое распространение во многих областях промышленности, техники и технологии [20, 27]. К наиболее востребованным материалам можно отнести различные титановые (с α+β-структурой) и стальные (аустенитно-ферритные, аустенитно-мартенситные, ферритно-бейнитные и др.) сплавы, которые стали популярными благодаря улучшенным по отношению к однофазным сплавам физико-механическим свойствам – коррозийной стойкости, конструкционной прочности и тугоплавкости [26, 28, 42].

В работе приводится краткий обзор физических многоуровневых моделей неупругого деформирования кристаллических материалов, которые учитывают изменение эволюционирующей внутренней структуры материала. Рассматриваются различные модификации физических теорий пластичности и их применение для описания поведения многофазных материалов, получивших широкое распространение в промышленности. Особое внимание уделяется критическому анализу приводимых моделей, выявлению основных недостатков существующих теорий, что служит основой для определения направлений дальнейших работ по рассматриваемой тематике.

1.    Экспериментальные исследования многофазных материалов

Хорошо известно, что поведение материала на макроуровне существенным образом зависит от текущего состояния эволюционирующей внутренней структуры на более низких масштабных уровнях – мезо- и микроуровнях [2, 9–11,13]. Неупругое деформирование существенным образом влияет на изменение структуры материала, которая в конечном счете и определяет макрохарактеристики готового изделия [3, 7]. Это подтверждает достаточно широкий класс экспериментальных работ, посвященных исследованию эволюционирующей структуры различных материалов [19, 23, 69 и др.].

Актуальной проблемой является исследование влияния на поведение металлов и сплавов межзеренных (и межфазных – в особенности) границ (в том числе взаимной ориентации фаз), поскольку границы могут выступать в качестве эффективного барьера, тормозящего подвижные дислокации, а также влиять на локализацию пластической деформации. Границы фаз играют ключевую роль в неупругом деформировании многофазных сплавов, поскольку приводят к скоплению дислокаций на границе, несовместности упругих и пластических деформаций. В работе [69] с помощью просвечивающей электронной микроскопии в опытах с бикристаллом, состоящим из аустенита и феррита, показано, что дислокационное скольжение начинается в аустенитной фазе. При дальнейшем деформировании скольжение протекает в ферритной фазе, при этом границы фаз выступают источниками дислокаций, инициируемыми концентраторами напряжений на границе. Стоит отметить, что при произвольной взаимной ориентации зерен следы скольжения дислокаций в аустенитной и ферритной фазе не совпадают, что указывает на несовместность систем скольжения (СС) различных фаз. Дислокации в ферритной фазе носят винтовой характер, поэтому поперечное скольжение обеспечивает большое количество дислокационных петель и однородность пластических деформаций по всей ферритной фазе, в аустенитной фазе присутствуют частичные дислокации, что указывает на низкую энергию дефекта упаковки (ЭДУ) этой фазы. В статье [19] с помощью метода электронной дифракции была исследована микроструктура двухфазной дуплекс нержавеющей стали SAF 2507, состоящей из аустенита (γ) и феррита (α, δ), выдержанной при температуре

900°C в разных временных диапазонах. Показано, что длительная выдержка приводит к отклонению от «идеальной» теоретической ориентировки [22].

В другой экспериментальной работе [23] рассматривается влияние мезо- и микроструктуры, в том числе отношения объемных долей аустенитной и ферритной фаз, их морфологии, кристаллографической текстуры материала, размера, формы, расположения и взаимной ориентации зерен/субзерен на макросвойства материала. Проводились натурные эксперименты на образцах из дуплекс стали 22Cr-6Ni-3Mo в опытах прямого и реверсивного кручения при температуре 1000 °С и скорости деформирования 1 с–1. Мезоструктура рассматриваемого материала имеет форму ферритной матрицы, окружающей «островки» аустенитной фазы. В процессе прямого кручения на срезах, параллельных плоскости сдвига, видно, что фазы аустенита вытягиваются в направлении сдвига; после реверсивного нагружения фазы аустенита разворачиваются перпендикулярно сдвиговой плоскости. Отмечается наличие двойников в аустенитной фазе. В работе приводится кристаллографическая текстура отдельно для аустенитной и ферритной составляющих материала в различные моменты деформирования. Приведены экспериментальные данные относительно углов разориентации между кристаллитами.

При высокотемпературной обработке во многих материалах могут протекать фазовые превращения, которые оказывают значительное влияние на отклик материала. Например, в работе [39] предлагается способ обработки образца нержавеющей стали коммерческой чистоты 304 с размером зерна около 200 нм, при этом в материале происходит формирование ячеистой дислокационной структуры при скольжении между зернами. Микроструктура указанной стали состоит из ГЦК- и ОЦК-фаз, которые видны на рентгеновской дифракционной картине. Первый этап обработки состоит в деформировании материала (примерно на 94 %) при комнатной температуре, затем – при температуре жидкого азота. Последний этап характеризуется мартенситным превращением ГЦК-фазы в тонкие пластинки ОЦК-фазы. Зеренная структура материала после 1-го этапа состоит преимущественно из фаз с ОЦК-решеткой и имеет ярко выраженную вытянутую форму. Такое состояние микроструктуры характерно для мартенситных превращений. Размеры фаз в двух направлениях почти одинаковы: в плоскости, перпендикулярной оси прокатки, ширина и толщина фаз мартенсита порядка 50–100 нм, длина мартенситных пластин 500– 1000 нм. Второй этап – отжиг при 575 °С в течение двух часов. Этот этап характеризуется обратным переходом ОЦК- в ГЦК-фазу (частично). Отожженная микроструктура мартенсита состоит из столбчатых зерен 200 нм в диаметре и 1000–2000 нм в длину. Эти зерна содержат субзерна ГЦК-фазы примерно 200 нм в длину. В статье приведены данные зависимости сопротивления деформированию, указаны температуры, при которых осуществляется квазистатическое нагружение при скорости 4,4·10–5 с–1. Резкое падение напряжений после 500 °С связывают с изменением микроструктуры материала и, следовательно, изменением механизмов деформирования (как именно – не отмечено). При 450 °С микроструктура имеет вытянутые зерна в направлении прокатки, образец при 550 °С состоит из примерно равноосных зерен.

Другие важные процессы с точки зрения описания неупругого поведения, протекающие при высоких гомологических температурах деформирования в многофазных материалах, – динамический возврат и рекристаллизация. В работе [44] рассматривается высокотемпературная деформация в диапазоне 900–1150 °С образцов из различных сплавов (сталей) при разных скоростях деформации (0,04–4c–1) в тесте на кручение. Образцы представляли собой стержни диаметром 15 мм трех классов сталей: ферритная X5CrTi25, аустенитная X3CrNiMo18-9 и двухфазная аустенитно-ферритная X2CrNiMoN22-5-3. Приведены снимки мезоструктуры материала, из которых следует, что в результате глубокого пластического деформирования (более 100 %) происходит процесс динамической рекристаллизации во всех трех сплавах. Зарождение и рост новых зерен осуществляется следующим образом: границы зерен удлиняются (вытягиваются) в процессе деформирования, затем происходит зарождение новых зерен на границах первоначальных кристаллитов и дальнейший их рост. Зародыши новых зерен образуются в результате слияния дислокационных ячеек или «размытия» границ первоначальных зерен (на снимках границы зерен не имеют четких очертаний). Можно отметить, что образцы из аустенитно-ферритного сплава демонстрируют наибольшие значения интенсивностей напряжения на диаграмме нагружения при различных температурах и скоростях нагружения, далее идет аустенитная сталь, затем – ферритная. Авторы работы считают, что различное поведение (отклик) материала связано со способностью к расщеплению дислокаций и созданию барьеров. Согласно снимкам, структура ферритного сплава характеризуется после деформаций порядка 100 % большими субзернами и небольшой плотностью дефектов по сравнению с аустенитом. В двухфазном материале для различного диапазона скоростей и температур деформирования бóльшая интенсивность структурных перестроек наблюдалась в фазе феррита. Значительное упрочнение двухфазной стали авторы связывают с процессами на межфазных границах.

В работе [57] рассматриваются релаксационные процессы, протекающие в поликристаллах после деформации и последующей выдержки – статический возврат и статическая рекристаллизация. Во время первого этапа деформирования пластическая деформация осуществляется по большей части в ферритной фазе, поэтому и упрочнение реализуется преимущественно в ферритной, а не в аустенитной фазе. Вследствие этого последующая выдержка приводит к процессу статического возврата во всех диапазонах рассматриваемых температур сначала в ферритной фазе, только затем – в аустенитной. Во время выдержки протекают процессы статической рекристаллизации в обеих фазах, но, по всей видимости, с различной интенсивностью – преимущественной в аустенитной фазе. В зависимости от температуры и времени выдержки образуется различная мезоструктура материала – мелко- или крупнозернистая, которая соответственно приводит к повышению или понижению предела текучести. Так, например, при температуре 1150 ° С и выдержке в течение 50 с образуется мелкозернистая структура, а при 100 с – крупнозернистая, чем и объясняются экспериментально полученные различия диаграмм нагружения. Отмечается, что по мере повышения температуры интенсивность релаксационных процессов увеличивается.

Следует отметить, что описанные выше результаты экспериментальных исследований свидетельствуют о наличии разнообразных физических процессов и явлений, протекающих в многофазных материалах при интенсивных пластических деформациях в различных диапазонах скоростей деформирования и температур. Например, при низких и средних температурах деформирования ключевую роль в процессе неупругого формоизменения материала играет внутризеренное дислокационное скольжение, в некоторых случаях – двойникование; высокотемпературное деформирование приводит к активизации других каналов релаксации упругих напряжений – рекристаллизации и возврату. В связи с этим весьма важным становится вопрос о выборе способа описания неупругого поведения материала. Достаточно широко распространен макрофеноменологический подход, основанный на большом количестве тщательно поставленных и проведенных экспериментов. Однако в силу влияния на текущее состояние внутренней структуры материала большого количества внешних (температура и скорость деформирования, схема нагружения и др.) и внутренних (фазовый и химический состав) факторов можно сделать вывод о неприменимости макрофеноменологического подхода, поскольку в случае применения последнего нет причин утверждать, что модель будет обладать универсальностью по отношению к действующим механизмам пластического деформирования, не говоря уже о моделях для еще несуществующих материалов (материалов с наперед заданными свойствами). Вследствие этого для корректного учета реальных физических механизмов перспективным представляется многоуровневый подход, в основу которого положено рассмотрение в явном виде эволюционирующей внутренней структуры материала - модели ФТП [8].

2.    Модели ФТП, применяемые для описания неупругого деформирования многофазных материалов

Следуя работе [8], укажем классификационные признаки в многоуровневых моделях. В качестве таковых могут выступать: а) число рассматриваемых масштабных уровней; б) гипотеза связи однотипных характеристик различных уровней; в) физические теории, положенные в основу моделей нижних масштабных уровней. Большинство современных многоуровневых моделей являются двухуровневыми (макро- и мезоуровень). В качестве элемента нижнего (мезо-) масштабного уровня обычно выступает кристаллит (зерно), а элементом макроуровня - некоторая совокупность кристаллитов. Ключевым классификационным признаком многоуровневых моделей является гипотеза связи соседних масштабных уровней (способ осреднения). Существует три основных класса таких моделей [8]: статистические, самосогласованные и прямые. К статистическим моделям можно отнести модели, которые рассматривают элементы низшего масштабного уровня с достаточной степенью независимости друг от друга; переход к более высокому масштабу для части характеристик осуществляется путем осреднения, для другой части - на основе принимаемых гипотез кинематического (гипотеза Фойгта), статического (гипотеза Рейса) или промежуточного типа (гипотезы типа Кренера). Самосогласованные модели основаны на рассмотрении элемента мезоуровня в окружении матрицы материала с эффективными характеристиками, определяемыми итерационным путем по свойствам элементов мезоуровня с использованием принятой процедуры осреднения последних. В прямых моделях можно выделить два типа. К первому относятся модели, в которых рассматривается решение краевой задачи для совокупности кристаллитов; для каждого кристаллита используется физическая конститутивная модель. Прямые модели второго типа являются комбинированными в том смысле, что для решения краевой задачи на макроуровне используются статистические модели. Численная реализация прямых моделей, как правило, основывается на методе конечных элементов.

Следует отметить, что прямые модели, особенно первого типа, широко используются для описания неупругого поведения многофазных материалов. В большинстве таких моделей в качестве конститутивных соотношений принимается анизотропный закон Гука в том или ином виде. Основным механизмом неупругого деформирования является сколь- жение дислокаций, а в качестве кинематической основы используется мультипликативное разложение на упругую и пластическую составляющие. Вследствие использования метода конечных элементов поля напряжений и деформаций являются согласованными, но вопрос взаимодействия дислокаций с границами различных фаз в указанных моделях остается открытым. Нередко упругопластическое поведение многофазных материалов описывают с помощью самосогласованных моделей. В многофазных материалах при определенных условиях могут происходить процессы, связанные с изменением фазового состава (рекристаллизация, фазовые переходы), и существует ряд работ, основанных на смешанном подходе – теории фазового поля и физических моделях. Встречаются модели, основу которых составляют макрофеноменологические модели, но с использованием нескольких масштабных уровней. Обычно рассматриваются два масштабных уровня, поэтому их можно назвать «двухмасштабными», но в отличие от двухуровневых моделей, в явном виде не вводятся переменные, описывающие физические механизмы деформирования. Также существуют попытки создания макрофеноменологических моделей для описания неупругого поведения многофазных материалов, но их нельзя признать успешными, поскольку, как отмечают и сами авторы [см., например, 60], для идентификации таких моделей необходимо огромное количество экспериментальных данных.

Ниже приводится краткий обзор математических многоуровневых моделей, которые применяются к описанию упругопластического или упруговязкопластического поведения многофазных материалов.

В работе [38] предложена прямая модель 1-го типа для описания неупругого деформирования двухфазной нержавеющей стали. Основу конститутивного описания материала составляет физическая упруговязкопластическая модель, в качестве определяющего соотношения использовался анизотропный закон Гука, кинематическое рассмотрение основывалось на мультипликативном разложении Ли–Кренера, критические напряжения сдвига определялись суммой накопленных сдвигов по системам скольжения (СС). Рассмотрены различные типы мезоструктуры двухфазного материала: объемная доля железа (остальная доля приходится на медь) составляла 0, 17, 50, 83 и 100 %. Проведена серия экспериментальных тестов на сжатие цилиндрических образцов при комнатной температуре и квазистатическом нагружении, полученные данные сравнивались с результатами моделирования.

Каждое зерно представляло собой монокристалл, поведение которого описывалось вязкопластической моделью. Основным механизмом неупругого деформирования полагалось движение дислокаций по СС, для которых принимался изотропный закон упрочнения. Применение прямой модели позволило учесть взаимодействие и влияние соседних зерен и фаз. Экспериментальные данные и результаты моделирования, в частности диаграммы нагружения, находятся в удовлетворительном соответствии для образцов из чистых железа и меди, для двухфазных материалов обнаружены отклонения. Обратные полюсные фигуры также обнаруживают удовлетворительное соответствие с натурными экспериментами для чистых материалов, для двухфазных образцов имеются весьма значительные расхождения. Несоответствие экспериментальных данных и результатов моделирования авторы объясняют несколькими причинами: локальные деформации и напряжения вблизи включений второй фазы могут существенным образом зависеть от формы включения, взаиморасположения включений, выбора конечных элементов; другой возможной причиной авторы называют неудовлетворительное описание изотропным за- коном упрочнения физических процессов, происходящих в материале. К сожалению, авторы цитируемой работы не обсуждают следующие важные моменты: моделирование начальной мезоструктуры двухфазного материала и ее соответствие приведенным в статье экспериментальным данным. Не рассматриваются процессы, происходящие на границах включений, сами включения (их размеры, плотность и т.д.) существенным образом влияют на движение дислокаций, однако в работе используется изотропный закон упрочнения. Влияние соседних зерен сводится к изменению полей перемещения и напряжений, определяемых методом конечных элементов (все остальные факторы отброшены).

В работе [21] рассматривается прямая физическая модель первого типа. По мнению авторов работы, к моделям физических теорий пластичности следует отнести континуальные модели, в явном виде учитывающие комплексное («сложное») скольжение дислокаций, их расщепление, пересечение и т.д. Для описания движения дислокаций используется тензорная (второго ранга) характеристика плотности дислокаций [43], которая является ключевой переменной в континуальной теории дислокаций и напрямую связывается с плотностью так называемых геометрически необходимых дислокаций, предложенных в работе [17]. Другой количественной мерой дислокаций является их скалярная плотность, отнесенная к системам скольжения. С помощью континуальной теории дислокаций авторами предлагается описывать коэффициенты «изотропного» упрочнения, но в работе они не конкретизируются.

Кинематическая основа модели строится на стандартном мультипликативном разложении Ли–Кренера на пластическую и упругую составляющие. Для описания скоростей сдвигов по системам скольжения используется вязкопластическое соотношение вида

_T( k ) - x ( ^k )| - r ( ^k )\ ”

^Y( k ) = ^Y0 (■---------( k 7------- ) sgn ( ^T( k ) - x ⁽ k ) ) ,

τc где τ(k) – сдвиговые напряжения; r(k) – напряжения, описывающие изотропное упрочнение; x(k) – напряжения кинематического упрочнения. Отмечается, что в большинстве работ, использующих соотношение для скоростей сдвигов данного типа, «изотропная» составляющая напряжения течения r(k) связывается со скалярной плотностью дислокаций на рассматриваемой системе. Другой возможный вариант определения r(k) основывается на введении дополнительной степени свободы кристаллита, связанной с его вращением, и переходе к обобщенному континууму Коссера. В результате предлагается соотношение (его вывод опущен) для нелинейного «изотропного» упрочнения:

N

r ^{( k} ) = r ₀ + Q ^ h k ( 1 - exp ( - b Y ⁽ i) ) ) + Hl _c к ^{( k}) , i = 1

где первое слагаемое авторы работы связывают с начальным критическим напряжением на СС, второе слагаемое описывает взаимодействие между дислокациями, расположенными на различных системах, а последнее – появление кривизны κ^{( k )} на данной системе скольжения. Следует отметить, что приведенное соотношение не является изотропным, тем не менее авторы статьи придерживаются такой терминологии. Конкретизация соотношения для напряжений кинематического упрочнения x ^{( k )} отсутствует.

Другим важным вопросом построения многоуровневых моделей, по мнению авторов работы, является проблема выделения масштабов и их связи, предлагается рассмотреть три уровня. Макроуровень, отвечающий совокупности зерен в рамках поликристалличе-ских агрегата, мезоуровень 1, который относится к зерну поликристалла, и мезоуровень 2, относящийся к локальным неоднородным полям напряжений, деформаций и внутренних переменных, возникающих в зернах поликристалла. Для связи масштабных уровней предлагается использовать самосогласованную схему, которая предполагает рассмотрение включения в однородной матрице. При определенных упрощениях связь напряжений принимает вид

a(n) = L + G (в - в( n)), в = ^ f(n)e(n)    в(n) = din(n) - Dd‘n(n) в(n)

n где G – модуль сдвига (для простоты материал полагается упруго-изотропным); din(n), duin(n) – тензор скорости неупругих деформаций и его интенсивность в n-м зерне; σ(n) – напряжение в n-м зерне, параметр D выбирается из условия близости тензора σ(n) в соответствующих зернах в поликристаллическом материале, полученном численно с помощью прямой модели, осредненным по представительному объему напряжениям Σ. Скорость пластических деформаций определяются осреднением по объему:

D ™ = ^ f ⁽ n ) d in ⁽ n )

n где f(n) – объемная доля n-й фазы.

Утверждается, что данный подход может быть использован для моделирования неупругого поведения многофазных материалов, содержащих смеси различных фаз. В этом случае каждая фаза приписывается отдельному зерну, а указанная модель может учитывать свойственную таким телам гетерогенность физико-механических свойств.

В работе [36] рассматривается конститутивная модель поведения двухфазного материала γ-TiAl и α 2 -Ti 3 Al. Структура материала представляет собой гранецентрированную кубическую тетрагональную решетку γ-фазы и гексагональную плотноупакованную решетку α 2 -фазы, вытянутых в виде ламелей. Соотношения физической модели теории пластичности материала были внедрены в конечно-элементный программный комплекс Abaqus (прямая модель первого типа).

В рамках модели полагается, что пластическая деформация может происходить параллельно ламельным плоскостям границ фаз за счет сдвигов (движения краевых дислокаций) по СС в «мягкой» γ-фазе; сдвиги, нормальные по отношению к плоскости границы, значительно ограничены вследствие существования «жесткой» α 2 -фазы. При этом определены межфазные компланарные системы скольжения; в γ-фазе СС делятся на три типа: «мягкая» СС 1 – плоскости соседних фаз совпадают, «мягкая» СС 2 – направления скольжения соседних фаз совпадают, «жесткая» СС – нет совпадающих плоскостей и направлений скольжения. Несмотря на это разделение, используется «стандартный» закон упрочнения вида

т;a1=E h ae|Y(B|, в где hав- матрица модулей упрочнения; Y(в) - скорость сдвига СС 0. Авторы отмечают, что установление значений модулей упрочнения сразу для двух фаз является трудоемкой за- дачей, поэтому эволюционные соотношения для критических напряжений сдвига учитывают взаимодействие только внутри одной фазы.

Проведена процедура идентификации модели, реализующая алгоритм Нелдера–Мида для решения задачи минимизации, которая заключается в поиске минимума отклонения интенсивности напряжений, определенных экспериментально и из численных расчетов для двух различных монокристаллов γ-TiAl и α 2 -Ti 3 Al. Показано соответствие результатов для двухфазного материала γ-TiAl и α 2 -Ti 3 Al. Следует отметить, что в работе не указывается различие между двумя типами границ (границами зерен между фазами и границами зерен одной фазы), сами границы учитываются неявно в законах упрочнения.

В работе [14] рассматривается прямая физическая модель 1-го типа, основанная на физической теории упруговязкопластичности. Отмечается, что для указанного класса двухфазных материалов важное влияние на отклик материала оказывает присутствие остаточного аустенита, который может претерпевать фазовые мартенситные превращения. В качестве определяющего соотношения используется анизотропный закон Гука в промежуточной (разгруженной) конфигурации. Упругая составляющая градиента места раскладывается на ортогональный тензор, сопровождающий деформацию, и симметричный тензор искажений; в упругом законе фигурирует именно вторая составляющая; после записи соотношения его можно преобразовать в актуальную конфигурацию ортогональным преобразованием. Собственно искажения решетки малы, поэтому допустима линеаризация закона Гука. По мнению авторов, такая форма записи хорошо подходит для металлов.

Рассмотрение кинематики деформирования основывается на мультипликативном разложении деформационного градиента на три составляющие, описывающие соответственно упругие искажения, пластическое деформирование и аустенитно-мартенситные превращения. К сожалению, авторы работы не рассматривают вопрос о последовательности используемого разложения. Трансформационные превращения предлагается описывать соотношениями, аналогичными уравнениям для пластических деформаций.

В работе приведено подробное описание алгоритма реализации модели мезоуровня, который основан на схеме Ньютона–Рафсона; предложена процедура идентификации параметров модели. Следует отметить, что данная работа не затрагивает проблемы описания взаимодействия различных фаз поликристаллического агрегата; не рассматривается также влияние температуры на пластическое деформирование кристалла, в том числе – на мартенситные превращения; опущены вопросы связи масштабных уровней; не отмечено влияние мартенситных прослоек на упругопластические свойства выделенного кристаллита.

В работе [66] рассматривается модель и результаты ее применения для анализа неупругого поведения двухфазных материалов – низкоуглеродистой мартенситной стали и аустенитной нержавеющей стали, содержащих аустенитные и мартенситные фазы. В работе используется прямая модель 1-го типа, основанная на физическом рассмотрении эволюции плотности дислокаций и внедренная в коммерческий конечно-элементный программный комплекс. Рассматриваются вопросы влияния взаиморасположения аустенитной и мартенситных фаз на неупругие макросвойства материала, а также локализацию пластических деформаций.

В цитируемой работе используются соотношения, предложенные и детально описанные в [55]. Кинематика деформирования основывается на аддитивном разложении градиентов скорости перемещений на упругую и пластическую составляющие. Неупругое де- формирование осуществляется скольжением по кристаллографическим системам, для описания скорости скольжения используется вязкий закон степенного вида. Принимается модификация соотношения для описания эволюции критических напряжений сдвига, предложенная в [31]:

N^

T-> = T ya >+ G у у» ) ^a"p m -^  ,

• V                        YV ^U0 y

где i y^a) - «статическое» критическое напряжение на системе скольжения a ; G - модуль сдвига; N s - число систем скольжения; b ^(в) - модуль вектора Бюргерса; a _ap - коэффициенты упрочнения систем скольжения; 0 - абсолютная температура; Oq - отсчетная температура; ^ - показатель термического разупрочнения, р _im - плотность неподвижных дислокаций.

Предполагается аддитивность плотности подвижных и неподвижных дислокаций [70], мобильные дислокации становятся неподвижными вследствие торможения дислокационными барьерами и дислокациями леса. Предлагаются эволюционные соотношения для мобильных и неподвижных дислокаций:

d ρ i ⁽ m^{k )} dt

d ρ ⁽ m^{k )} dt

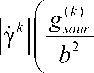
ρ im

( k )

IY⁽ k )1       k )    Р⁽ k )

^Y       g mnter +r m

- g ⁽ k ) Р ⁽ k )

mnter m

b

-

^g immob

b

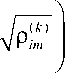
( k )        ( k ) ( k )

^ρ im     ^g recov ^ρ im

Здесь g _s ⁽ _o ^k _u ⁾ _r – коэффициент, описывающий увеличение плотности мобильных дислокаций в результате действия дислокационных источников; g _m ^{( k} _n ⁾ _ter – коэффициент, описывающий торможение мобильных дислокаций дислокациями леса или вследствие дислокационного взаимодействия; g _i ⁽ _m ^k _m ⁾ _ob – коэффициент остановки подвижных дислокаций; g _r ⁽ _e ^k _c ⁾ _ov – коэффициент перестройки и аннигиляции мобильных дислокаций. Вышеперечисленные коэффициенты определяются кристаллографией материала и процессами генерации, взаимодействия и восстановления плотности дислокаций, которые рассмотрены в работе [55].

Предложенная модель позволяет описывать лидирующие механизмы взаимодействия аустенитной и мартенситной фазы – формирование стыков дислокаций в аустенитной фазе и аннигиляцию дислокационных стыков вокруг внешней границы остаточного аустенита в мартенситных блоках, что приводит к упрочнению аустенита, разупрочнению мартенсита и локализации пластических деформаций. Более того, высокие напряжения вокруг границы мартенсита и остаточного аустенита могут вызвать мартенситные трансформации, которые препятствуют разрушению.

В работе [34] представлена прямая двухуровневая модель 2-го типа для описания двухфазного материала, содержащего матрицу аустенита с внедрениями MnS. Мезоструктура материала (зерна аустенита и распределение частиц MnS) имеет следующие характеристики: зерна аустенита имеют размеры порядка 30 нм; объемная доля фаз MnS – около 5 %, среднее расстояние между включениями 30 нм, размеры включений MnS около 10 нм.

Для описания скоростей сдвига дислокаций предлагается использовать модифицированное соотношение Орована с учетом термической активации и движения дислокаций в двух противоположных направлениях:

' t⁽ k ) A V '

v к 9 _v

у ( k ) = p b ² v exp I--I sinh

V к9 )

где у ⁽ k ) - скорость сдвига k -й СС; p, v - плотность, скорость подвижных дислокаций; A F -свободная энергия Гельмгольца активации дислокационного движения; θ – температура; к - константа Больцмана; т ^{( k} ) A V - работа поля напряжений; A V - активационный объем. Торможение дислокаций связывается с появлением геометрически необходимых дислокаций, для плотности которых записывается эволюционное соотношение.

На основании численных расчетов делается вывод, что влияние ориентации частиц MnS на отклик материала является более существенным по сравнению с влиянием ориентаций аустенитной фазы. Также отмечается, что некоторые ориентации границ аустенит – MnS приводят к значительной локализации деформации на границе, поэтому изотропное упрочнение материала не описывает физические эффекты взаимодействия дислокаций с границей кристаллитов. Следует отметить отсутствие сравнения численного моделирования с экспериментальными данными.

В работе [65] предложено физическое описание неупругого поведения многофазной углеродистой стали с учетом фазовых превращений. Представлены результаты моделирования с использованием прямой модели первого типа. Отмечается, что даже низколегированная сталь без дорогостоящих примесных элементов Cr и Ni может обладать высокой прочностью и ковкостью. Мезоструктура такого материала при комнатной температуре состоит из частиц феррита, бейнита, термического мартенсита и изолированных зерен остаточного аустенита. Последние могут претерпевать мартенситные фазовые превращения под действием механических нагрузок. Такой эффект носит название трансформационно-индуцированной пластичности (transformation-induced plasticity –TRIP). Следует отметить, что мартенситные прослойки могут возникать и при термическом воздействии в сталях с локальной концентрацией углерода выше 1,4 %. В качестве рабочей гипотезы принимается, что описание механически индуцированного мартенсита подобно термически индуцированному.

Для описания неупругого поведения в рассмотрение вводятся четыре масштабных уровня: мезоуровень – уровень аустенитного зерна, окруженного ферритной матрицей, верхний микроуровень – совокупность мартенситных прослоек в аустенитной фазе, нижний микроуровень – отдельные мартенситные прослойки и, наконец, уровень решетки кристаллита. Отмечается, что на скорость мартенситного превращения влияет размер и ориентация зерен аустенита. Делается предположение, что пластические деформации могут происходить в ферритной матрице, а аустенит может деформироваться только упругим образом. В силу этого для остаточного аустенита в мультипликативном разложении Кренера–Ли остаются два сомножителя, описывающие упругие искажения кристалла N fe и трансформацию из аустенита в мартенсит: f tr = E + ^ ^(а)уTb(aW") (n(a) - нормаль га-а=1

битусной плоскости; b ^(α) –единичное направление трансформации; γ T – величина мартенситной деформации; ξ^(α) – объемная доля мартенсита; N – число вариантов мартенсита).

В качестве ОС используется анизотропный закон Гука, записанный в терминах промежуточной конфигурации:

k = п : с e .

■ f e - E )

– упругая составляющая

1 T

Здесь k - второй тензор Пиола-Кирхгоффа; с e = 2 ( ( f )

тензора деформации Коши-Грина, тензор упругих свойств определяется соотношением

NN п =----1 J 1 -У ^ (a) п A + 1 + yt b(a) ■ n(a) У^а)п(а) ^, det (ftr )Ц = J ( TT ) = где пA – тензор упругих свойств аустенита; п(α) – тензор упругих свойств мартенсита α-й системы; множитель (1 + уTb(a) ■ n(a)) описывает объемное расширение вследствие фазового превращения.

Для описания термодинамики трансформационной пластичности в рассмотрение вводятся свободная энергия Гельмгольца у ( с _e , 9,^ ) , которая включает в себя упругую энергию тела у _т ( с _e ,£ ) , термическую составляющую у th ( 0,^ ) и поверхностную энергию тела у ₅ ( ^ ) ; приводятся конкретные соотношения для всех вышеуказанных составляющих. С помощью введенного потенциала определяется движущая сила мартенситного превращения, с использованием которой формулируется критерий мартенситного превращения.

Предложенная модель позволяет описать экспериментальную зависимость, характеризующую увеличение критических напряжений, при которых осуществляются мартенситные превращения при уменьшении размера зерна, и ориентационную зависимость скорости трансформационных деформаций. Следует отметить, что в статье отсутствует полная замкнутая математическая постановка задачи неупругого деформирования; не описан процесс идентификации параметров; отсутствует описание физического механизма TRIP-эффекта; не указан способ описания взаимодействия различных фаз.

В работе [64] предложена модель для описания поведения двухфазного сплава никеля, которая внедрена в конечно-элементный коммерческий программный комплекс. Используется трехуровневая модель: элементом мезоуровня 1 (в статье он называется микроуровнем) являются отдельные фазы материла γ и γ`, описываемые соответствующей конститутивной моделью; элементом мезоуровня 2 является конгломерат (совокупность) двух фаз (в статье – мезоуровень); элементом макроуровня – совокупность элементов мезоуровня 2. Отмечается, что связь между элементами мезоуровней 1 и 2 посредством гипотезы Фойгта или Рейса является неприемлемой, поэтому используется модифицированная гипотеза Рейса:

f l^k ) о ,

где о l k ( a l k ) - тензор напряжений фазы / к (индекс p - precipitate) и / ^ (индекс m -matrix); fⁱ – объемные доли фаз; σ – осредненный тензор напряжений мезоуровня.

Так как фазы обладают разными физико-механическими свойствами, они по-разному реагируют на прикладываемую нагрузку. Предлагаются дополнительные условия на границе раздела фаз:

– условие совместности между фазой l _k ^m и фазой l _k ^p на k -й границе, определяемой нормалью n ^k ,

Elk •(I - ПkПk ) = Elm •(I -ПkПk ), где εi – тензор деформаций i-й фазы; I – единичный тензор; – равенство усилий на границе раздела двух фаз k:

σ

klm k

• n = a ^k • n .

Механизмом неупругого деформирования является скольжение дислокаций, при этом дислокации раскладываются на две составляющие – статистически накопленные дислокации и ГНД, для которых вводится плотность дислокаций и записываются эволюционные соотношения.

Для скорости сдвига используется вязкопластическое соотношение вида

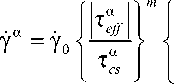
1 - exp

к

I f)

т or

r sign ( ^T f ) ,

где tOs — критические напряжения сдвига; тor - напряжения Орована (необходимы для изгиба дислокационной линии между двумя фазами); тf - эффективные напряжения СС а, а а „а „а eff misfit b , где та - сдвиговые напряжения; т^ - обратные микронапряжения (backstress), обусловленные ГНД; T°mSfftt - напряжения несоответствия, появляющиеся в результате несоответствия параметров решеток (типа) и некогерентности границ фаз.

Особенностью численной реализации данной модели является наличие специфической подобласти (для этого выделяются несколько КЭ) – границы между двумя фазами, которая, как предполагают авторы, играет важную роль в формировании отклика материала. Все эффекты, связанные с границей двух фаз, определяются только внутри этой области.

В работе [47] рассматривается физическая модель, описывающая поведение сплава Ti–6Al–4V, основу которого составляет α-матрица с ГПУ-решеткой, занимающая примерно 60 % общего объема. В результате охлаждения из расплава выделяются остаточные β-пластинки с ОЦК-структурой и объемной долей около 10 %. Третья возможная структура в указанном сплаве относится к вторичной α-фазе и обладает пластинчатой формой. Для анализа вторичную α-фазу и остаточную β-фазу выделяют в единую ламельную однородную часть и обозначают α+β. Взаимоориентации решеток этих фаз устанавливаются известными кристаллогеометрическими соотношениями [52, 16]. Отмечается актуальность моделирования внутренней эволюционирующей структуры материала, поскольку последняя может заметно улучшать рабочие свойства образцов, изготовленных из рассматриваемого материала.

В работе достаточно подробно обсуждаются вопросы реализации пластической деформации в основной α-фазе с ГПУ-решеткой. Отмечается, что границы зерен и фаз являются основным препятствием для движения дислокаций, а основным носителем пластической деформации являются винтовые дислокации, залегающие в базисной (0001) или пирамидальной { 1011 } плоскостях. В ламельной а+в-структуре механизмы пластической деформации изучены менее основательно, чем в матрице, поэтому при неупругом моделировании предлагается не рассматривать отдельные пластинки каждой фазы, а рассмотреть целиком структуру α+β с осредненными пластическими свойствами.

Используется стандартное мультипликативное разложение Кренера–Ли градиента места; для описания пластической деформации в рассмотрение вводятся СС, определяемые вектором Бюргерса и нормалью к плоскости скольжения. Скорости сдвига на каждой СС определяются вязкопластическим соотношением вида

/I_т( * ) - _т( * )| - _х( * )\ m

^Y( *' = Y о ( ---------( * у-------- ) sgn ( ^т( *' ^- X ⁽ *' ) ,

τc где Y0 — отсчетная скорость сдвига; т(*' - сдвиговые напряжения; тЬ*' - «обратные мезонапряжения» (порядка 5 МПа); χ(k) – пороговые напряжения (90–500 МПа); τ(ck) – критические напряжения (100–1000 МПа в зависимости от СС); m – параметр скоростной чувствительности. Критические напряжения принимаются постоянными, т(*' = 0. Для «обратных напряжений» используется соотношение Армстронга–Фредерика, учитывающее как упрочнение материала, так и динамический возврат:

т b*' = hD (bY(k > - Tbk > |Y(k 'I), где b и hD – параметры упрочнения. Пороговые напряжения принимаются постоянными для всех СС, кроме призматических, для которых учитывается эффект Холла–Петча, основанный на рассмотрении свободного пробега дислокаций:

X1*' = X о + *y (dа Г5 + A (т( *' - т2*'), где параметр χ0 описывает «вязкие» напряжения на каждой системе скольжения; ky – константа Холла–Петча; d α – средний размер зерна α-фазы. Последнее слагаемое описывает влияние расщепления полной винтовой дислокации на четыре частичные, параметры A, т(*', т(2*' определяются экспериментально.

Предлагаемая в работе модель позволила удовлетворительно описать вязкопластическое поведение двухфазного титанового сплава Ti–6Al–4V, учесть влияние скольжения дислокаций на наведенную анизотропию и текстуру материала. Показано влияние параметров, описывающих микро- и мезоструктуру, на макроотклик материала. Несмотря на трехмерную постановку задачи, вычисления были проведены для двумерного случая; программный код модели материала был встроен в конечно-элементный комплекс Abaqus. Остается до конца неясным вопрос описания движения винтовых дислокаций соотношениями, полученными для краевых. Не затронут вопрос взаимодействия различных фаз.

В работе [68] рассмотрено применение прямых моделей, основанных на физической теории пластичности, для описания поведения двухфазных сплавов типа γ-TiAl. Пред- ставлен анализ механического поведения и структуры, которая исследовалась с помощью наноиндентора на тонких пленках, на основе полученных данных моделировалась мезоструктура всего двухфазного материала. Конститутивная модель была внедрена в программный комплекс, использующий МКЭ. В работе учитываются две моды неупругого деформирования – скольжение краевых дислокаций и двойникование. Отмечается, что эти два механизма деформирования способны описать эволюцию микроструктуры материала (TiAl), удовлетворительно соответствующую экспериментальным данным. Рассматриваемый двухфазный материал имеет ламельную структуру (ламельная прослойка является второй фазой), поэтому отклик материала будет существенным образом зависеть от угла между осью нагружения и «пластинами» второй фазы. Для моделирования отклика материала рассматривался представительный объем из 64 зерен с периодическими граничными условиями. Результаты моделирования показали хорошее соответствие экспериментальным данным. Следует отметить, что в работе не рассматриваются вопросы идентификации параметров модели, а также механизмы взаимодействия разнородных фаз.

В работе [59] рассматривается двухуровневая модель, основанная на теории фазового поля, ориентированная на описание упругопластического поведения сталей и сплавов, в том числе – многофазных поликристаллических материалов. Отмечается, что в металлах с низкой или средней ЭДУ могут происходить процессы рекристаллизации материала, которые значительным образом изменяют структуру материала на микро- и мезомасштабах. В этом случае физико-механические свойства макроуровня должны зависеть от текущего состояния внутренней структуры, что необходимо учитывать при моделировании.

В рассмотрение вводятся два масштабных уровня: мезо- и макроуровень. Структурным элементом мезоуровня является зерно поликристалла, для описания которого вводится индикаторная функция ϕ i , принимающая значение 1 в зерне i -й фазы и 0 – для нулевой концентрации этой фазы. С помощью индикаторной функции определяется фазовый состав в точке пространства, а далее используется предлагаемая авторами модель для нахождения НДС материала. Эволюционное уравнение для функции φ i предложено в работе [56]:

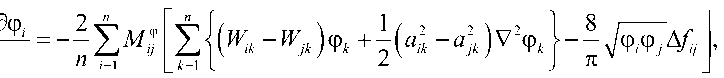
д^ i = -2 51 n где aij – градиентные коэффициенты; Wij – коэффициенты, описывающие влияние энергетического барьера между зернами; Mj - матрица коэффициентов, отражающих мобильность фаз. Для всех вышеперечисленных параметров предложены соотношения, которые выражаются через толщину и поверхностную энергию границ зерен. Параметр Δfij – запасенная энергия между i-й и j-й фазами, которую предлагается связать с собственной энергией дислокаций в изотропной упругой среде 1/2Gb2 (G – модуль сдвига, b – величина вектора Бюргерса). Для описания отклика материала предлагается воспользоваться соотношением [18]

о u = а Gb Тр , где α – параметр взаимодействия дислокаций; ρ – средняя плотность дислокаций в зерне. Процесс рекристаллизации начинается при достижении критического значения плотности дислокаций.

На макроуровне используется закон Гука в скоростной релаксационной форме, предложенный в работе [41]:

K ^J

П - — K d K d

: D .

Здесь П – тензор упругих коэффициентов; Kd – девиаторная часть тензора напряжений Пиола–Кирхгоффа; KJ – производная типа Яуманна тензора напряжений Пиола– Кирхгоффа; D – тензор деформации скорости; g – параметр, определяемый соотношением g = K d: K d

1 3 EtE I

1 +

4 GE - E J где E – модуль Юнга; Et – касательные модули. Связь масштабных уровней осуществляется посредством гипотез: с макро- на мезоуровень передается температура и тензор ско-,                                                                - do рости деформации, а с мезо- на макроуровень - касательные модули E = —-.

_{d £} и

Предложенная в работе модель позволяет описывать макромеханические свойства материала с учетом эволюционирующей структуры материала; показано, что при уменьшении среднего размера кристаллитов интенсивность рекристаллизации возрастает. Следует отметить, что авторы работы «завязывают» математическую постановку задачи на метод ее решения (метод конечных элементов). Существенным для данного типа задач является температура и ее градиенты, однако постановка задачи является изотермической, а температура входит в соотношения как постоянный параметр. Остаются некоторые сомнения относительно приемлемости определяющего соотношения макроуровня, в который наряду с тензором упругих свойств входят изотропные упругие модули, а тензор Пиола–Кирхгоффа 2-го рода и тензор деформации скорости определены в различных конфигурациях.

В работе [37] предложена модель для описания процесса статической рекристаллизации в сталях, которая начинается преимущественно в аустенитных зернах. Используется подход, основанный на физической теории пластичности и теории фазового поля. Как отмечают авторы работы, статическая рекристаллизация играет ключевую роль в формировании мезоструктуры аустенитных сталей в процессах высокотемпературного деформирования и отжига материалов, а свойства макроуровня существенно зависят от текущего состояния мезо- и микроструктуры.

Для описания отмеченных процессов, как правило, используются одномерные мак-рофеноменологические модели типа JMAK (Johnson–Mehl–Avrami–Kolmogorov) или трехмерные макрофеноменологические модели, с которыми можно ознакомиться в работе [54]. Отмечается, что вышеупомянутые модели (одномерные и трехмерные) имеют ряд недостатков, например не позволяют учитывать топологию и морфологию зерен, а также локальные деформации вблизи границ зерен. Вследствие этого предлагается собственный подход к моделированию указанного процесса. Для генерации исходной зеренной структуры представительного объема материала используется алгоритм, основанный на многогранниках Вороного, а на границе рассматриваемого объема накладываются условия периодичности. Для описания неупругого деформирования материала используется упруговязкопластическая физическая теория [58], в качестве определяющего соотношения принимается анизотропный закон Гука, релаксация упругих напряжений происходит за счет дислокационных сдвигов по системам скольжения, для скоростей сдвига используется степенное соотношение Хатчинсона, в качестве закона упрочнения применяется

«стандартное» соотношение для критических напряжений сдвига, описывающее взаимодействие дислокаций с дислокациями леса. Далее полается, что система стремится уменьшить свою свободную энергию, которая, по мнению авторов, определяется в первую очередь кривизной границ зерен и накопленной энергией в условиях изотермичности [25], откуда получены следующие соотношения:

Ф /=HL^my

s j Ф^Ф у

- фу ^фу +   (Ф/. - фу) + П J^AGi

2n         J n где φi – фазовая переменная, характеризующая объемную долю i-й фазы; η – толщина границ зерен; mij – параметры мобильности (миграции) границы; sij – поверхностная энергия смежных границ; ΔGij характеризует вклад накопленной энергии деформации Ed; ве- личина кi = фiV 2фj

2 π

-ФJV фу+ут(фi -Фу) 2η2

описывает кривизну межзеренной границы.

Полагается, что эволюция критических напряжений на СС описывается соотношением вида тc = т0 + aGb Jp, а энергия образовавшихся дислокаций (накопленная энергия де- формаций) – Ed = αρGb2 . Комбинируя два последних соотношения, можно показать, что

E d определяется выражением

E d

(^ c ^jo)!

α G

где τ₀ , τ _c – начальные и текущие критические напряжения сдвига; G – модуль сдвига; α – постоянный параметр, физический смысл которого не указан в работе.

Предложенный подход позволил описать эволюцию микроструктуры сплава 25MoCrS4; численные и экспериментальные данные показывают качественное соответствие. Следует отметить, что модель реализована для двумерного случая, что значительно ухудшает ее прогностические свойства; кроме того, при описании накопленной энергии неявно принимается гипотеза изотропии кристаллита.

В работе [67] исследуется поведение двухфазной стали, мезоструктура которой состоит из включений жесткой мартенситной фазы, окруженных мягкой ферритной. Образец, изготовленный из указанного сплава, подвергался следующим опытам: одноосное нагружение (растяжение/сжатие), затем разгрузка, поворот оси деформирования в пространстве и последующее нагружение. На основе экспериментальных работ [32] делаются выводы, что в двухфазных сталях разгрузка отклоняется от закона Гука, наблюдается разупрочнение и более ярко выражен эффект Баушингера. Выделяются следующие особенности двухфазной стали: a) образование мартенситных фаз приводит к появлению остаточных микронапряжений на начальной стадии деформирования материала; б) различные физико-механические свойства двух фаз приводят к высоким неоднородным полям напряжений.

В работе используется упругопластическая модель типа Линя с применением самосогласованного подхода, в котором зерно (фаза) представляло собой сферическое включение в однородную бесконечную матрицу. Приведены обширные результаты по анализу эволюции критических напряжений сдвига различных СС при смене направления деформирования, на основании которых объясняется эффект Баушингера; представлены результаты зависимости отклика материала от угла излома траектории деформации. Отме- чается, что причины, обусловливающие возникновение остаточных микронапряжений в однофазном материале, более ярко выражены в двухфазном материале. В работе можно выделить следующие недостатки: не обсуждаются вопросы, связанные с границами двухфазного материала (прохождения дислокации через границу); результаты моделирования не сопоставляются с экспериментом.

В работе [15] рассматривается двухмасштабная феноменологическая модель двухфазной ферритно-мартенситной стали. На мезоуровне используется модель пластического течения, а макросостояние определяется осреднением по объему величин мезоуровня -используются гипотезы Фойгта/Рейса. Предложенная модель реализована с помощью МКЭ в двумерном случае. Исследуется вопрос оптимального сочетания фаз для поиска требуемых механических свойств материала. Отмечено, что свойства поликристалличе-ского агрегата существенным образом зависят от соотношения объемных долей фаз мартенсита и феррита. Так, например, увеличение объемной доли мартенсита приводит к увеличению интенсивности напряжений на диаграмме нагружения, но только до 55 % деформации, затем наблюдается снижение. Также отмечается, что в материале присутствует неоднородность деформаций между фазами феррита и мартенсита - сначала деформируются «мягкие» фазы феррита, затем «жесткие» мартенсита.

На основе экспериментальных исследований предложен механизм развития пластической деформации: неупругие деформации зарождаются в мягкой ферритной матрице, а при исчерпании возможностей к необратимому деформированию «мягкой» фазы последняя распространяется и на «жесткую» мартенситную. С помощью полученной модели показано, что даже небольшие неупругие деформации в мартенситных прослойках приводят к значительному изменению отклика всего материала. В работе можно отметить следующие недостатки: взаимодействием между фазами/границами фаз пренебрегается; отсутствуют описания процедур идентификации/верификации модели; рассматривается плоская задача, результаты которой могут существенным образом отличаться от трехмерной; не указывается, каким образом происходят изменения объемных долей фаз, как влияет это на их морфологию; ОС мезоуровня являются изотропными; не обосновывается выбор схемы осреднения.

В работе [40] предложена феноменологическая макроскопическая модель, описывающая пластическое деформирование стали с легирующими добавками магния. Отмечается, что модель должна описывать поведение материала в достаточно широком диапазоне температур и скоростей нагружения. В указанном классе материалов при глубокой пластической деформации могут происходить процессы, значительно влияющие на мезо-и микроструктуру материала, такие, например, как динамическая рекристаллизация, процессы упрочнения, динамический возврат, которые существенным образом видоизменяют последнюю, что находит отражение в макросвойствах. По мнению авторов, особую роль в пластическом деформировании играет процесс рекристаллизации, который приводит к разупрочнению материала.

На основе анализа экспериментальных данных макроуровня авторы работы выделяют четыре основные характеристики макрофеноменологического описания неупругого поведения исследуемого материала: напряжения текучести о y , критические напряжения рекристаллизации о Cr , напряжения насыщения рекристаллизации о Sat и напряжения установившегося течения о ss . Упрочнение материала предлагается описывать соотношением, учитывающим температуру и скорость деформации, полученным в [24] для одноосного нагружения:

d ° = ₀ 1 ( ° - ° y ⁽ °,g) ' d&      0     ( ° Sat ( ^0,ё ) - ° y ( ⁰-),

° Sat ( ^0, S ) - ° y ( ⁰Л ) °_E - ° y ( ^0,& )

В этом соотношении ε – величина деформации; σ ε – напряжение течения; θ 0 определяет атермический вклад в упрочнение, которое описывается соотношением

θ

° Sat ( ^0,& ) - ° y ( ^0,& )

2ε r

где ε r – деформация релаксации. Для определения напряжения σ y предлагается использовать соотношения модели Sellars–Tegart–Garofalo (STG) [33,53]:

° , ( ⁰ .Ё ) = ° . ⁺ ° H, Sinh ~'

Z, (0,e)

1/ m_y

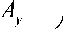
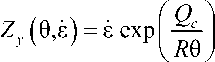
Здесь ° _a , ° _Hy , A y , Q c , m y - материальные параметры, определяемые экспериментально. Для напряжений насыщения и критических напряжений рекристаллизации используются однотипные соотношения, аналогичные приведенным выше, но со своими материальными параметрами. В случае если напряжения течения превышают критические, происходит разупрочнение материала и изменение объемной доли рекристаллизованного материала.

В цитируемой работе приведен краткий обзор работ, описывающих динамическую рекристаллизацию и разупрочнение в поликристаллических материалах при высокотемпературной деформации. Для идентификации и верификации модели проведено более 30 натурных экспериментов при различных температурах и скоростях деформирования; результаты моделирования показали достаточную степень согласованности с экспериментальными данными. К недостаткам работы следует отнести отсутствие анализа физических процессов, протекающих в кристаллах, огромное число экспериментальных данных, необходимых для идентификации модели.

В работе [49] рассматриваются различные схемы осреднения для моделирования упругопластического деформирования двухфазных (многофазных) материалов; численная реализация модели проведена методом КЭ. Отмечается, что каждая фаза обладает различными физико-механическими свойствами, поэтому возникает необходимость моделирования их в отдельности. В статье рассматриваются модели среднего поля (“mean field homogenization”). Данные подходы основаны на выделении элемента представительного объема (“representative volume element”) или домена, характеристики которого полагаются однородными в пределах данного объема; различные фазы рассматриваются как однородные области в составе всего агрегата. Элемент представительного объема (домен) является макроскопической точкой и точкой интегрирования в методе КЭ.

Оператор осреднения микроскопических величин для ПО определяется как

{g(x )L= ^Jg(x)dV - где g - любая полевая величина, определенная в пределах элемента ПО; ^g (x)^. - осред-ненное значение величины g. Предполагается, что объем, по которому производится осреднение, может быть представлен в виде декомпозиции отдельных доменов:

(g(x)k =IJ g(x) dVk=Е fAg(x)V ш=U шк, Vk шк                  к                             к где fk = Vk/V – объемные доли субдоменов.

Отмечается, что механическая работа на макро- и мезоуровнях должна быть эквивалентна, поэтому выполняется условие

• о : Ё = (о) : (е) = (о : е) . \ / ш \ / ш \       / ш

Напряжения и деформации макроуровня определяются осреднением. Следуя предположению, что каждая фаза обладает собственным откликом, используем линейное соотношение для субдоменов:

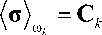
Для решения упругих и упругопластических задач данным методом необходимо задавать либо напряжения, либо деформации. Таким образом, задается связь между уровнями:

• (е) = A, : (е) , \ / ш к ^к \ / ш

• (о) = В^ : (о) . ш к ^к ш

В цитируемой работе анализируются различные схемы осреднения, которые основываются на разных соотношениях, используемых для определения тензоров A k , B k – гипотезе Фойгта, гипотезе Рейса, методе Эшелби, самосогласованном методе, методе Мори– Танака, методе интерполяции Лайнса (“Lielens interpolation method”), связанном методе интерполяции (“bound interpolation method”) и методе упругопластического осреднения.

Подход, основанный на моделях среднего поля, развивается в статье [50], в которой рассматривается многофазная TRIP-сталь, состоящая из следующих фаз: аустенита, мартенсита, феррита и бейнита. Феррит и бейнит объединяются в одну фазу, чтобы уменьшить количество фаз. Предлагаются два подхода к решению задачи. Первый состоит в том, что аустенит рассматривается как включение в матрицу феррит–бейнит, содержащую мартенсит; во втором аустенит и мартенсит рассматриваются как отдельные фазы в матрице феррит–бейнит. Результаты, полученные интерполяционным методом и самосогласованной схемой, показали хорошее соответствие экспериментальным данным. В работах предложен алгоритм решения данного типа задач; показано, что гипотеза Фойгта и гипотеза Рейса определяют соответственно верхнюю и нижнюю границы интенсивности напряжений материала на диаграмме нагружения (все остальные схемы осреднения дают промежуточный между ними результат). Эффект взаимодействия фаз и их границы не исследуется.

В работе [45] рассматривается модель молекулярной динамики двухфазного бикристалла Fe+Cu, содержащего 30 000 атомов. Кристаллиты материала ориентированы относительно ЛСК следующим образом (указываются направления вдоль осей X, Y, Z соответственно): Fe [111], [1 10], [ 112^ , Cu [110], [111], [ 112] . Таким образом, плоскость сколь- жения ОЦК-материала (110) была разориентирована относительно плоскости (111) ГЦК на угол 30°. В бездефектный кристаллит вводится краевая дислокация (экстраплоскость), прикладываются сдвиговые напряжения, и наблюдается поведение этой дислокации. Отмечено, что дислокацию можно характеризовать наибольшими значениями энергии атомов края экстраплоскости.

Показано, что границы зерен/фаз являются не только существенным препятствием для движения дислокаций (роль упрочения за счет границ), но также и источником дислокаций. Возможность прохождения дислокации через границу зависит от параметров кристаллической структуры зерен/фаз, типа границы зерен/фаз и типа дислокации (краевая, винтовая, смешанная). К недостаткам работы можно отнести следующее: исследована только одна ориентация ГЦК/ОЦК зерен; рассмотрение большого количества дислокаций могло дать результаты моделирования более близкие к натурным экспериментам; не предлагается физическое объяснение результатов моделирования.

В работе [30] рассматриваются модели обобщенного континуума, описывающие неупругое деформирование кристаллических материалов. Отмечается три основных направления развития градиентных моделей для описания поведения кристаллических тел: 1) модели, в которых рассматриваются градиенты внутренних переменных, 2) модели, использующие градиенты перемещений второго порядка, и 3) модели, основанные на континууме Коссера. Основу указанного класса моделей составляет термодинамический подход.

Для примера рассмотрим градиентную теорию второго порядка, предложенную в работе [48] и в дальнейшем модифицированную для описания неупругого деформирования на основе физических теорий пластичности в [29]. В качестве независимых параметров рассматриваются вектор перемещений u , первый V u и второй градиенты перемещений Wu . В приближении малых градиентов перемещений полагается справедливой гипотеза аддитивности упругой и пластической составляющих градиентов перемещений и вторых градиентов перемещений

£ = £ e + £ p, П = П e + П p, где £ = 2(Vu + uV) - тензор малых деформаций; £e, £p

– его упругая и пластическая со-

ставляющие; n = V £ - градиент тензора малых деформаций; n e , П p — его упругая и пластическая составляющие. Отмечается, что не тривиальным является вопрос о корректном задании граничных условий, с которым можно детально ознакомиться в работе [35].

Далее определяется свободная энергия Гельмгольца ψ, которая вводится как функция состояния, аргументами которой служат упругая составляющая деформации ε ^e , упругая составляющая градиента тензора деформаций η ^e и внутренняя переменная модели q , описывающая упрочнение. Согласно принципу энтропии записываются уравнения состояния (определяющие соотношения):

дш „. дш „ дш о = р--, M = р---, R = р—, д£e          dqe          д q где σ – тензор напряжений, M – тензор моментных напряжений. Диссипативная функция для каждой материальной частицы определяется соотношением

D = о : £p + M л np - Rq, где символ « л » обозначает тройное скалярное произведение. В [29] предлагается использовать свободную энергию в форме, приводящей к определяющим соотношениям вида анизотропного закона Гука и аналогичного соотношения для моментов напряжения с дополнительным внутренним параметром, характеризующим масштаб le:

о = П 1 : £ e , M = ( I^е ) 2 П ₂: n e .

Для описания диссипативных (пластических) процессов вводится «потенциальная» функция f ( о , M , R ) и соответствующие ей термодинамические силы:

•р      a f     ._р -a f           -a f

£ p = ^1    , n p = ^?     , q = -X,

1 до         2 ам         3 ar где λi – пластические множители. Далее предлагается модифицировать закон Шмида на случай градиентной модели второго порядка и конкретизировать функцию f в следующей форме:

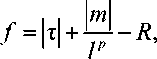
т = о : bn ,

m = M л bnb .

Тогда из предыдущих соотношений следуют соотношения для пластических составляющих £ p и n p :

£ p = Ypbn, np = Y5 bnb, где Yp — скорость пластического сдвига; Y5 — сдвиговая градиентная переменная, которая связана с Yp соотношением

X = Y p sgn ( т ) = l^p Y ⁵ sgn ( т ) .

Рассматриваемые в цитируемой работе модели обобщенного континуума применимы для описания коллективного движения дислокаций в узких ламельных структурах, которые, как правило, имеют двухфазную природу. В силу существования границ фаз, пластическая деформация будет существенно неоднородной на масштабе выделенного кристаллита, что нельзя учесть в рамках классического континуума. Введение в рассмотрение вторых и более высоких градиентов перемещений позволяет описать влияние размера зерна на пластическое деформирование, например эффект Холла–Петча. Другое применение теории автор видит в описании разрушения кристаллических материалов. Следует отметить, что гипотеза малых деформаций не позволяет рассматривать интенсивные пластические деформации; остаются вопросы относительно введенных масштабных параметров l^e и l^p .

Заключение

Приведен краткий обзор работ по многоуровневым моделям и физическим теориям пластичности, ориентированным на описание упругопластического и вязкопластического деформирования многофазных материалов. Следует отметить, что обзор не претендует на полноту и завершенность, поскольку рассматриваемая тематика является весьма актуальной и наблюдается существенный количественный рост числа публикаций по указанному направлению. Выбор источников цитирования определен наиболее актуальными, по мнению авторов, направлениями, в силу чего не лишен субъективности.

Работа выполнена при финансовой поддержке Минобрнауки РФ (базовая часть государственного задания ПНИПУ, № гос. регистр. 01201460535), РФФИ (проекты № 13-01-96006-р_урал_а, 14-01-00069-а, 14-01-96008-р_урал_а).