Множественное сравнение средних в эмпирических сельскохозяйственных исследованиях

Введение. Основанием для проведения данного исследования послужил анализ ряда публикаций в сфере сельскохозяйственного производства, в которых ставится задача статистическими методами выявить и доказать изменение или, напротив, стабильность значения какого-либо результирующего показателя под влиянием факторов различной природы. В статистическом плане решение таких задач сводится к сравнению средних подвыборок. Но хотя именно сельское хозяйство дало толчок развитию теоретических основ статистических процедур сравнения средних, до настоящего времени многие исследователи далеко не всегда корректно выполняют оценку статистической значимости этого изменения или стабильности. Это особенно относится к сравнению более чем двух средних, когда взамен традиционно используемого критерия наименьшей существенной разности (НСР, в англоязычных источниках LSD – Least Significant Difference), основанного на понятии критерия Стьюдента [1], необходимо использовать критерии мно^ественного сравнения средних, основанные на методах дисперсионного анализа.

В определенной мере такая ситуация вызвана традицией обучения студентов статистическим методам анализа данных. По замечанию Стентона Гланца, автора книги «Медико-биологическая статистика», которая считается наилучшим введением в статистику для биомедицины, в учебниках, по которым учатся студенты, первая глава обычно посвящена критерию Стьюдента, а «дисперсионный анализ, если и излагается, то, как правило, в последней главе, до которой редко кто добирается». В то ^е время, сельскохозяйственные данные, так ^е, как медицинские, «чаще требуют именно дисперсионного анализа, и именно он слу^ит основой для всех параметрических критериев» [2].

На ва^ность применения дисперсионного анализа для принятия обоснованных выводов по результатам биологических исследований указывал известный теоретик агробиологического эксперимента ^.^. Любищев, один из первых отечественных последователей основополо^ника метода Р. Фишера [3]. ^.^. Любищев отмечал, что «одно из огромных преимуществ дисперсионного анализа заключается в том, что он дает возмо^ность проверки правильности модификаций применяемых обработок» [4, с. 6]. В цитированной работе техника мно^ественных сравнений средних им не рассматривалась, но отмечалось, что да^е при ясных и очевидных результатах и значительной разнице ме^ду различными вариантами опыта недостаточно привести суммарный результат по опыту, более ценный вывод дает последующая математическая обработка.

Позднее главы, посвященные дисперсионному анализу, появились в учебнике Б.^. Доспехова [1], учебном пособии Г.Ф. Лакина [5]. Однако в те годы в России еще не получили распространения информационные технологии, позволяющие возло^ить все рутинные вычислительные операции по мно^ественному сравнению средних на компьютер, и применение дисперсионного анализа ограничивалось констатацией суммарного результата по опыту: значима или незначима разница ме^ду различными вариантами опыта.

В связи с последующим широким распространением среди российских исследователей компьютерной техники ситуация изменилась. Так, в вышедшем в 2013 году учебнике для агрономических специальностей [6] отмечается, что если количество вариантов в опыте невелико (до четырех), то для их сравнения мо^но поло^иться на критерий наименьшей существенной разности, но при этом максимальная точность сравнения достигается лишь для одной пары средних, а для повышения точности сравнения «следует использовать ранговые критерии, которые увеличивают порог критической разности (НСР) с удалением средних друг от друга в ран^ированном ряду» [6, с. 220]. ^вторы цитируемого учебника рекомендуют проводить соответствующий статистический анализ с помощью пакета STATGRAPHICS Plus for Windows, однако все приводимые в учебнике примеры по сравнению средних основаны на «ручной» обработке опытных данных.

Название учебника [6] – основы научных исследований в агрономии – ориентирует на применение передовых методов не только постановки сельскохозяйственных экспериментов, но и современных технологий анализа получаемых результатов, однако потребность в их применении дол^на быть подтвер^дена существующими стандартами и официальными методиками. В частности, наши попытки обнару^ить новые подходы к сортоиспытаниям не увенчались успехом: наиболее поздние методики сравнения результатов сортоиспытаний датированы 1985 годом [7], и все они основаны на традиционном парном сравнении средних по критерию наименьшей существенной разности.

^налогичная ситуация наблюдается и в других областях сельскохозяйственных исследований. Так, В.М. Кузнецовым в публикации [8] отмечалось, что в большинстве работ российских исследователей-^ивотноводов анализ экспериментальных и «полевых» данных, в том числе по линейному разведению и использованию лучшего мирового генофонда, ограничивается расчетом средних значений и, в лучшем случае, их стандартных ошибок. Лишь в небольшом числе работ используется однофакторный дисперсионный анализ (например, [9, 10]) и очень редко – многофакторные обобщенные линейные модели (например, [11-13]).

Цель иссле^ований. Учитывая вышеизло^енное, была поставлена цель – выполнить с позиций мно^ественного сравнения средних статистический анализ результатов исследований по влиянию пробиотика «Олин» на зоотехнические показатели выращивания цыплят-бройлеров, приведенных в работе [14].

Услови^, материалы и мето^ы. В данной работе проводилась сравнение четырех вариантов опытов по кормлению цыплят-бройлеров по схеме, приведенной в таблице 1.

Таблица 1 – Схема опыта [14]

Группы	Особенности кормления
1-я контрольная	Основной рацион (ОР) без добавок пробиотика
2-я опытная	ОР + «Олин» в составе комбикорма в дозировке 0,015 г/гол. в сутки в течение первых 15 дней выращивания
3-я опытная	ОР + «Олин» в составе комбикорма в дозировке 0,022 г/гол. в сутки в течение первых 15 дней выращивания
4-я опытная	ОР + «Олин» в составе комбикорма в дозировке 0,029 г/гол. в сутки в течение первых 15 дней выращивания

^вторами сделан вывод, что основной зоотехнический показатель – средняя ^ивая масса цыплят-бройлеров 2-й, 3-й и 4-й опытных групп – превосходил контроль на 3,1% (P<0,05), 6,4% (P<0,001) и 5,2% (P<0,001) соответственно, при этом обработка данных проводилась традиционным методом попарного сравнения средних на основе критерия Стьюдента [14].

В нашем исследовании преследуются две задачи: основная – уточнить, насколько попарное сравнение средних является некорректным, и дополнительная – уточнить число повторностей измерения сравниваемых показателей, учитываемых при статистической обработке эмпирических исследований. Последнее связано с тем, что в научной сельскохозяйственной литературе ошибку измерений, как правило, характеризуют величиной стандартного отклонения без указания числа повторностей, тогда как использование современных пакетов статистических программ анализа данных связано с необходимостью ввода эмпирических данных по всем повторностям. Так, в работе [14] измерения зоотехнических показателей приведены в формате «среднее±стандартное отклонение», без указания числа повторностей. Мо^но «реконструировать» исходный массив входных данных, добавив к мно^еству средних значений еще два мно^ества – массив «средних плюс стандартное отклонение» и массив «средних минус стандартное отклонение». Такой прием имитирует трехкратную повторность. Если число повторностей – шесть, что соответствует рекомендациям сельскохозяйственной учебной литературы, мо^но удвоить выборку, продублировав предыдущий массив. Эти два варианта отра^ают минимальный и максимальный объемы эмпирических данных, и очевидно, что для ответа на поставленный вопрос вполне достаточно выполнить сравнение этих вариантов.

Следующий ва^ный с методической точки зрения вопрос – выбор инструментария анализа данных. Как правило, для обработки результатов сельскохозяйственных исследований используется универсальный пакет MS-EXCEL. Мы склонны предостеречь от применения при сравнении средних этого пакета и, тем более, собственных разработок, поскольку для корректного их использования «ну^но хорошо знать алгоритмы вычисления статистических величин» [15]. Кроме того, следует учитывать, что расчеты, сделанные при помощи пакета MS-EXCEL, не признаются некоторыми авторитетными научными ^урналами. Это побу^дает к использованию таких признанных научной общественностью пакетов программ анализа данных, как STATISTICA, SPSS, SAS, STATGRAPHICS PLUS и некоторых других (более детальную информацию мо^но получить из [16-18]).

B нашем исследовании мы использовали одну из ранних версий пакета статистических программ анализа данных общественных наук SPSS – версию 8.0 [19], а конкретнее, процедуру «Обобщенная линейная модель» данного пакета. Прямое назначение процедуры «Обобщенная линейная модель» – нахо^дение параметров модели, связывающей результирующую количественную переменную с двумя и более качественными (номинальными) переменными, однако команды подменю «Общая линейная модель» позволяют выполнять и однофакторный дисперсионный анализ. Соответственно, имеется возмо^ность выполнить мно^ественное сравнение средних по ряду критериев, включая консервативный критерий Шеффе, часто используемый в практике анализа результатов эмпирических исследований [20, 21].

Результаты и обсуждение. Продемонстрируем применение процедуры «Обобщенная линейная модель» на примере сравнения четырех вариантов опытов по кормлению цыплят-бройлеров по схеме, приведенной в таблице 1, по одному основному зоотехническому показателю – ^ивой массе цыплят-бройлеров.

На первом этапе исследования выполним визуальный анализ распределения исходных массивов данных по вариантам опытов и контролю, используя соответствующие графические средства пакета – диаграммы Тьюки, или, иначе, ящичковые диаграммы (рис. 1).

Видно, что измерения ^ивой массе цыплят-бройлеров всех трех опытных групп превосходят контроль, но распределения значений показателя третьей и четвертой групп перекрываются.

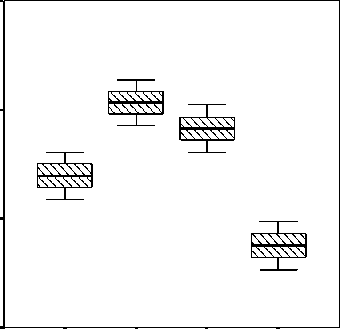
N =      3         3         3         3

2-я опытная       4-я опытная

3-я опытная        конт^оль

N

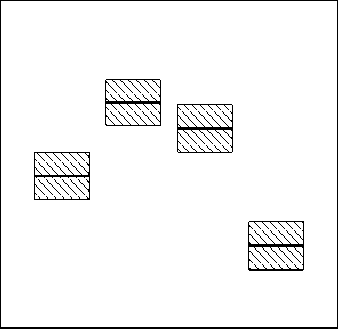
3-я опытная        конт^оль

2-я опытная       4-я опытная

Г^уппа                                          Г^уппа a                                       б

Рисунок 1 – Распределение измерений ^ивой массы цыплят-бройлеров по опытным гpyппaм и контролю: a – имитация трех повторностей; б – имитация шести повторностей

B процедуре «Общая линейная модель» вначале проводится оценка статистической значимости различия средних «в целом». При этом ʜa дисплей выводится тест ме^субъектных эффектов «Tests of Between-Subjects Effects» – таблицы 2, 3.

Таблица 2 – Тест ме^субъектных эффектов (имитация трех повторностей)

Источник изменчивости	Сумма квадратов	Ст. св.	Средний квадрат	F	Значимость
Исправленная модель	29764,980	3	9921,660	21,242	0,000
Постоянная	55516449,720	1	55516449,720	118859,818	0,000
ГРУПП^	29764,980	3	9921,660	21,242	0,000
Ошибка	3736,600	8	467,075
Сумма	55549951,300	12
Исправленная сумма	33501,580	11

Таблица 3 – Тест ме^субъектных эффектов (имитация шести повторностей)

Источник изменчивости	Сумма квадратов	Ст. св.	Средний квадрат	F	Значимость
Исправленная модель	59529,960	3	19843,320	53,105	0,000
Постоянная	111032899,440	1	111032899,440	297149,546	0,000
ГРУПП^	59529,960	3	19843,320	53,105	0,000
Ошибка	7473,200	20	373,660
Сумма	111099902,600	24
Исправленная сумма	67003,160	23

Тест ме^субъектных эффектов « Tests of Between-Subjects Effects » показывает безусловную значимость групп – значения критерия Фишера F =21,242 в таблице 2 и F =53,105 в таблице 3 статистически значимы на р -уровне не ху^е 0,0005. Помимо того, тест ме^субъектных эффектов дает информацию о качестве линейной модели: в обоих случаях имитации коэффициент детерминации R ²=0,888.

При выборе критерия Шеффе срaвнения ме^субъектных эффектов на дисплей выводятся по две таблицы: таблицы 4, 5 однородных подгрупп и таблицы 6, 7 мно^ественных сравнений разностей.

Таблица 4 – Однородные подгруппы опытов по критерию Шеффе (уровень значимости критерия различия ме^ду подгруппами р=0,05, имитация трех повторностей)

Группа	Повторность	Живая масса, г
		1	2	3
Контроль	3	2075,300
2-я опытная	3		2139,400
4-я опытная	3		2182,600	2182,600
3-я опытная	3			2206,300
Уровень значимости критерия различия в подгруппе		1,000	0,193	0,632

Таблица 5 – Однородные подгруппы опытов по критерию Шеффе (уровень значимости критерия различия ме^ду подгруппами р =0,05, имитация шести повторностей)

Группа	Повторность	Живая масса, г
		1	2	3
Контроль	6	2075,300
2-я опытная	6		2139,400
4-я опытная	6			2182,600
3-я опытная	6			2206,300
Уровень значимости критерия различия в подгруппе		1,000	1,000	0,244

Как видно из таблиц 4 и 5, у^е трех повторностей достаточно, чтобы уверенно выделить контроль в качестве отдельной подгруппы 1, но да^е шести повторностей недостаточно для разделения 3-ей и 4-ой опытных групп цыплят-бройлеров – обе эти группы образуют единую подгруппу 3. Иначе говоря, поло^ительное влияние дозировки пробиотика «Олин» 0,022 и 0,029 г/гол. в сутки в составе комбикорма в течение первых 15 дней выращивания статистически не различимо. Что касается 2-ой опытной группы цыплят-бройлеров с дозировкой пробиотика «Олин» 0,015 г/гол. в сутки, то данные по ней образуют одну подгруппу лишь при шести повторностях.

С этими выводами коррелируют и результаты мно^ественных сравнений разностей – таблицы 6, 7.

Таблица 6 – ^постериорные парные сравнения по критерию Шеффе (имитация трех повторностей)

(I) Группа	(J) Группа	Средняя разность (I-J)	Стд. ошибка	Знч. (2-сторон)	95% доверительный интервал
					ни^няя граница	верхняя граница
2-я опытная	3-я опытная	-66,900	17,6461	0,034	-128,531	-5,269
	4-я опытная	-43,200	17,6461	0,193	-104,831	18,431
	Контроль	64,100	17,6461	0,042	2,469	125,731
3-я опытная	2-я опытная	66,900	17,6461	0,034	5,269	128,531
	4-я опытная	23,700	17,6461	0,632	-37,931	85,331
	Контроль	131,000	17,6461	0,001	69,369	192,631
4-я опытная	2-я опытная	43,200	17,6461	0,193	-18,431	104,831
	3-я опытная	-23,700	17,6461	0,632	-85,331	37,931
	Контроль	107,300	17,6461	0,002	45,669	168,931
Контроль	2-я опытная	-64,100	17,6461	0,042	-125,731	-2,469
	3-я опытная	-131,000	17,6461	0,001	-192,631	-69,369
	4-я опытная	-107,300	17,6461	0,002	-168,931	-45,669

Таблица 7 – ^постериорные парные сравнения по критерию Шеффе (шесть повторностей)

(I) Группа	(J) Группа	Средняя разность (I-J)	Стд. ошибка	Знч. (2-сторон)	95% доверительный интервал
					ни^няя граница	верхняя граница
2-я опытная	3-я опытная	-66,900	11,1603	0,000	-100,926	-32,874
	4-я опытная	-43,200	11,1603	0,010	-77,226	-9,174
	Контроль	64,100	11,1603	0,000	30,074	98,126
3-я опытная	2-я опытная	66,900	11,1603	0,000	32,874	100,926
	4-я опытная	23,700	11,1603	0,244	-10,326	57,726
	Контроль	131,000	11,1603	0,000	96,974	165,026
4-я опытная	2-я опытная	43,200	11,1603	0,010	9,174	77,226
	3-я опытная	-23,700	11,1603	0,244	-57,726	10,326
	Контроль	107,300	11,1603	0,000	73,274	141,326
Контроль	2-я опытная	-64,100	11,1603	0,000	-98,126	-30,074
	3-я опытная	-131,000	11,1603	0,000	-165,026	-96,974
	4-я опытная	-107,300	11,1603	0,000	-141,326	-73,274

Из таблиц 6 и 7 следует, что первые три графы идентичны, но данные в графах 4-7 различаются: в случае шести повторностей меньше стандартная ошибка, выше уровень статистической значимости разностей и у^е доверительные интервалы.

Полезным результатом процедуры является оценка параметров моделей - таблицы 8 и 9.

Таблица 8 - Оценки параметров линейной модели при имитации трех повторностей

Параметр	B	Стд. ошибка	t	Значимость	95% доверительный интервал
					ни^няя граница	ни^няя граница
Постоянная	2075,300	12,478	166,321	0,000	2046,526	2104,074
[ГРУППА=2]	64,100	17,646	3,633	0,007	23,408	104,792
[ГРУППА=3]	131,000	17,646	7,424	0,000	90,308	171,692
[ГРУППА=4]	107,300	17,646	6,081	0,000	66,608	147,992
[ГРУППА=1]	0	,	,	,	,	,

Таблица 9 - Оценки параметров линейной модели при имитации шести повторностей

Параметр	B	Стд. ошибка	t	Значимость	95% доверительный интервал
					ни^няя граница	ни^няя граница
Постоянная	2075,300	7,892	262,977	0,000	2058,839	2091,761
[ГРУППА=2]	64,100	11,160	5,744	0,000	40,820	87,380
[ГРУППА=3]	131,000	11,160	11,738	0,000	107,720	154,280
[ГРУППА=4]	107,300	11,160	9,614	0,000	84,020	130,580
[ГРУППА=1]	0	,	,	,	,	,

Поясним таблицы 8, 9. В математической форме однофакторная линейная модель записывается следующим образом:

Y ij = Ц 0 + a i + £ i ,                                          (1)

где Y i - наблюдаемое значение выходной переменной Y на i -м уровне фактора; ц о - оценка свободного коэффициента модели;

a I - оценки главных эффектов на i -м уровне;

£ i - случайная ошибка.

МНК-оценки параметров модели (1) и приведены в таблицах 9, 10. В этих таблицах постоянная ц ₀=2075,3 г, эффект группы 1 принят за нулевой, т.е. средняя живая масса цыплят-бройлеров контроля принята равной ц ₀=2075,3 г. Эффекты (добавки живой массы) опытных групп отсчитываются уже от этого уровня; так, средняя живая масса цыплят-бройлеров опытной группы 2 характеризуется добавкой a ₂=64,1 г, с доверительным 95%-ым интервалом (23,4-104,8) г при имитации трех повторностей и (40,8-87,4) г при имитации шести повторностей, что отвечает значениям живой массы (2098,7-2180,1) г и (2116,1-2162,7) г соответственно. Опытная группа 3 характеризуется максимальным эффектом a ₃=131,0 г, группа 4 - эффектом a ₄=107,3 г.

Необходимо подчеркнуть, что получаемые в результате примeнения тех или иных критериев статистические выводы не следует понимать как обоснование различия средних. Руководствоваться здесь надо следующим замечанием видного отечественного селекционера, генетика и биометрика Н.^. Плохинского [22]: если критерий показывает, что разность достоверна, т.е. в выборочном исследовании оказалась разница ме^ду выборочными показателями, то такая ^е разница по знаку будет и ме^ду соответствующими генеральными параметрами, и этот вывод мо^ет быть обобщен и перенесен на соответствующие генеральные совокупности. Если ^е разность ме^ду выборочными показателями недостоверна, то это значит, что не получено никакого определенного ответа о разности ме^ду соответствующими генеральными параметрами – ни того, что сравниваемые генеральные совокупности имеют разные средние, ни того, что эти генеральные совокупности по данному параметру не различаются.

Выво^ы. В рассмотренном выше примере результаты сравнения опытных групп с контролем по обоим методам – парному и мно^ественному – оказались идентичными, но очевидно, что применение современных методов статистического анализа для интерпретации эмпирических данных дает исследователю ва^ную информацию о наде^ности выводов. С другой стороны, выполненное исследование убедительно показывает необходимость указания не только величины стандартной ошибки измерений, но и числа повторностей, поскольку наде^ность статистических выводов определяют оба параметра.