Mobile phone ranking by analytical hierarchical process: a case study

Published Online November 2018 in MECS DOI: 10.5815/ijieeb.2018.06.06

Buying and selling products with the use of e-commerce sites are common in present times. These sites are also used to make comparisons of the available products therein and in other places. These sites are also capable to differentiate among the specifications of the products by heuristics approaches. Buyers face many problems while they try to identify the best products based on their preferences and multiple criteria (often defined as specifications but collection of specifications may be termed as criteria). Decision making for identifying suitable products sometimes becomes very confusing with the change of policies of the sellers and available alternative offers across the websites. These problems are usually studied in the area of Multi Criteria Decision Making (MCDM).

With the increase of the number of websites, proper product selection has become a hectic task for web users especially for mobile phone buyers. There are various models of decision making for identifying the best suitable product among huge number of available products across multiple platforms like web sites, mobile applications, local markets and news papers. Over the years, researchers have tried to provide the actual requirements of web users. But still the available methods are not completely capable of providing exact solution of this problem yet. And also, available methods do produce some erroneous results sometimes. Hence, to meet exact users’ requirements has become a challenging task for which we have tried to develop a method for the selection of mobile phones from an e-commerce website. AHP has been observed as an analytical tool to help web users for MCDM problems by ranking the products according to their priority. One of the most crucial steps in decision making system is the accurate estimation from the analysis of the relevant data and AHP can perform this step significantly. In this paper, we have used AHP for evaluating the priority of a product based on some criterion. Data, used by AHP for analysis, required to be normalized as a preprocessing task to avoid inconsistent results.

The paper is organized in the following way- Section II briefly describes related works. Detailed description of proposed methodology using AHP has been discussed in section III, where as in section IV, the dataset along with the pair wise comparison matrices has been defined and experimental results have been depicted. We can easily observe that our result coincides with the desired result. Finally, our work has been concluded in section V.

• II.    Related Works

Analytic Hierarchy Process (AHP) is one of the important tools having the potential of solving MCDM problems in an efficient manner. In the following we briefly discuss various existing works related to the use of AHP-

AHP has been used as a measurement tool with ratio scales with special emphasis on consistency measurement [1]. Subdivisions of AHP for justification of rank preservation have also been depicted in [1]. AHP was used in [2], based on Eigen vector for identifying best information system reengineering project. High Eigen vector got the highest priority according to this methodology. In [3], AHP and TOPSIS models have been combined to implement a decision support system that can be used for evaluation of performance of village government. For assessment of locating fire stations, combination of indexing system method with AHP has been applied in [4] where AHP has been used for classification and qualification of the numerous types of regions. An analysis of the theory of corporate social responsibility, risk management and the exact method of AHP has been performed in paper [5] that has been used in the decision making purposes. Paper [6] suggested AHP for importance extraction and prioritization of use case. This use case is also used to verify whether the customer’s idea can be determined through consistency assessment of AHP or not. Paper [7] presented a demonstration on AHP which shows that the value of different aspects of green buildings can be perceived in various ways. It also presented a conceptual technique for the identification of consumer ranking and weights of a major green building rating systems categories. AHP has been used as a tool for MCDM problem in [8] and also some practical and computational difficulties has been examined there. Paper [9] gave a brief demonstration on survey of a real world problem of an auto glass company. AHP was used to provide a solution for Carglass Turkey’s location selection problem which was a MCDM problem including both tangible and intangible factors. In paper [10], researcher illustrated the application of the AHP to the evaluation of bank mergers and acquisitions strategy. The proposed model for this suggested problem was explored with the assistance of the board of directors of a billion-dollar bank holding company. Paper [11] described how the application of AHP was advantageous in measuring the intangible and complex impacts of the Trans-Sumatra Highway built in the late 1970’s. The methodology used AHP for exploring the overall impact of the highway according to the feedback of local people for cost estimation. AHP methodology has been used in [12] for complex medical decision making system to develop a rating system for allocation of livers for orthographic transplantation. Five major criterions have been considered there such as logistic consideration, tissue compatibility, medical status, waiting time and financial considerations. MCDM problem considered as a major issue in [13] which used AHP to decide whether a nuclear plant should be developed or not and also in later, the advantages and drawbacks has been discussed. In paper [14], a new concept called the technology development envelope has been developed which was used to transform the technology road mapping approach to a dynamic, flexible, and easy to operate methodology. This new approach ordered an efficient way that helps the organizations to overcome the challenge of keeping a roadmap alive. Paper [15] showed that the usual multiplicative synthesis of alternative priorities for benefits, opportunities, costs and risks, obtained from separate analytic hierarchy or network models, can produce similar results which mean that the result is ambiguous. In [16], researchers have proposed an objective scoring system for intellectual property patents from the licensor side using the AHP for valuation of the patents for new products being developed by an actual enterprise. AHP can be used to predict demand for hotel and help the management from crises arising due to demand fluctuations in their business. The most vital phenomenon of the proposed model is that it is adaptable for modification and be further polished in the future which is elaborated significantly in [17]. In [18], AHP has been used to develop a model for internet technology outsourcing decision and this model has also been verified by applying it to an outsourcing decision for a renowned locomotive company.

• III.    Proposed Methodology for Providing Mobile Phone Ranking Using AHP

Buyers can judge various mobile phones based on certain judgmental criteria. AHP performs various mathematical comparisons and calculations to rank available mobile phone alternatives depending on multiple judgmental criteria. The method of AHP forms pair wise comparison matrices of criteria and alternatives for different calculations. Consistency checking is done to test the qualities of comparisons. Consistency checking also ensures the acceptability of the AHP solutions of multi-criteria decision making problems. Finally, composite priority weight values are calculated for each alternative and alternatives are ranked according to their composite priority weight values. We describe the step by step procedure of mobile phone ranking using AHP in the following –

Step 1: Goal Formulation.

Step 2: Use of various judgmental criteria to achieve the goal.

Step 3: Consideration of different alternatives.

Step 4: Formation of pair-wise comparison matrices.

Step 5: Calculation of Priority Vectors (PV), largest Eigen values and consistency checking from the pair-wise comparison matrices formed in step 4.

Step 6: Calculation of composite Priority Weight (PW) values of each alternative from the PV values calculated in step 5 and ranking of alternatives.

In the following, we discuss the above mentioned steps in details-

Step 1: Goal Formulation

A goal needs to be formulated for AHP. AHP performs several numerical calculations to reach the goal. The goal of the proposed system is to select the most suitable mobile phone for a buyer.

Step 2: Use of various judgmental criteria

There are many judgmental criteria for mobile phones these days. These criteria are used by AHP to achieve the goal. The judgmental criteria used in our system are discussed in the following-

• a.    Price (P)

Price of a mobile phone is a very important criterion. Most of the people like to filter mobile phones depending on price. This criterion reflects the economical aspect of a buyer. This criterion being one of the vital criteria for mobile phone selection can play an important role in AHP.

• b.    Battery Backup (BB)

In today’s time mobile phones are used for various purposes. Different applications run on mobile phones to serve different purposes of users. Hence, the battery backup capacity has become a necessary criterion for selecting a mobile phone. This hardware oriented criterion also can add important information in AHP regarding the process of decision making.

• c.    Users’ Review (UR)

Users of a mobile phone share their experiences of using the phone through their reviews. These feedbacks cover different important aspects of any mobile phone like: its functional advantages-disadvantages, hardware and software issues, longevity, user friendliness etc. In short, reviews of users create a much clear view for the new buyers. Thus, users’ reviews make the decision making task of a new buyer regarding phone selection easier. The overall coverage of this criterion can influence AHP at highest extent.

Step 3: Consideration of different alternatives

A buyer has to select one mobile phone from many alternatives. Ranking of alternative choices generated by AHP helps user in mobile phone selection process. We have considered M 1 , M 2 and M 3 as the mobile phone alternatives for AHP to operate on.

AHP operates on the hierarchical mapping of goal, criteria and alternatives. Goal of a problem forms the top level of the hierarchy. Judgmental criteria are placed in the next level and the bottom most level is made of the alternative choices. The mapping between different levels of the hierarchy is very critical. Proper mapping is essential for achieving the formulated goal. Fig.1. shows the hierarchy of our problem.

Goal

Judgmental

Criteria

Mobile Phone

Alternatives

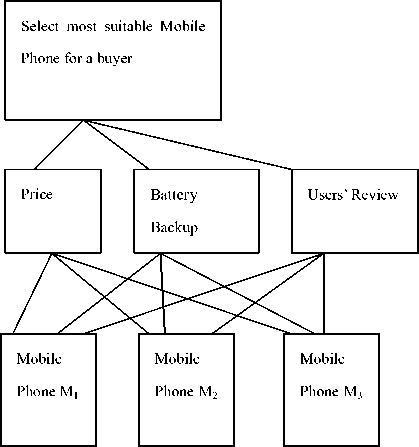
Step 4: Formation of pair-wise comparison matrices

AHP involves the formation of pair-wise comparison matrices. Pair-wise comparisons are done: between different judgmental criteria with respect to goal and between different alternative choices with respect to each judgmental criterion. Comparisons between judgmental criteria are done to find the relative importance of each judgmental criterion towards the goal. Again, comparisons between alternatives with respect to each judgmental criterion are done to evaluate relative importance of each alternative with respect to each judgmental criterion.

Solving a problem with n judgmental criteria and m alternative choices needs to form: one nxn pair-wise comparison matrix for comparing n judgmental criteria with respect to goal or desired objective and w (w≤n) number of mxm pair-wise comparison matrices for comparing m alternatives with respect to each of the w number of dominating and most effective judgmental criteria. The method of selection of w number of dominating judgmental criteria out of n judgmental criteria is discussed in step 5 of section III. Now, let’s consider that JC y (y=1,2,3...n) denotes a judgmental criterion and A x (x=1,2,3...m) denotes an alternative. Also consider that JCCMat denotes the nxn matrix and JCRACMat y (y=1,2,3...n) denotes a mxm matrix with respect to judgmental criteria JC_y. The structures of JCCMat and JCRACMat_y are shown in Table 1. and Table 2. respectively.

Table 1. Structure of JCCMat

JC 1       JC 2      JC 3 .

.JC n

Elements of JCCMat and JCRACMat y represent the pair-wise comparison values. These pair-wise comparison values are obtained as per the scale of relative importance developed by Saaty [1]. Table 3. shows the basic scale of Saaty to obtain the relative importance value of pair-wise comparison made between two activities. In our problem, an activity can be a JC y (y=1,2,3...n) or can be a A x (x=1,2,3...m).

Table 3. Saaty’s basic scale of relative importance

Intensity of Importance	Definition	Explanation
1	Equal importance.	Two activities contribute equally to the objective.
3	Weak  importance of one over another.	Experience and judgment slightly favor one activity over another.
5	Essential or strong importance.	Experience and judgment strongly favor one activity over another.
7	Demonstrated importance.	An activity is strongly favored and its dominance demonstrated in practice.
9	Absolute importance.	The evidence favoring one activity over another is of the highest possible order of affirmation.
2,4,6,8	Intermediate values between the two adjacent judgments.	When   compromise   is needed.
Reciprocals	If activity i has one of the above nonzero numbers assigned to it when compared with activity j, then j has the reciprocal value when compared with i.

JC 1

JC 2

JC 3

a11       a12     a13....................a1n a21       a22     a23...................a2n a31       a32      a33..................a3n

JC n

a n1      a n2

Table 2. Structure of JCRACMat y

A 1       A 2     A 3 .

.A m

A 1

A 2

A 3

b11        b12     b13

b21      b22     b23

b31      b32     b33

A m

b m1

Based on the basic scale of Saaty, a pq (p,q=1,2,3... n) and b rs (r,s=1,2,3...m) can have their values from the set S={1,2,3,4,5,6,7,8,9,1/2,1/3,1/4,1/5,1/6,1/7,1/8,1/9}. It can easily be found that a pp =1 (p=1,2,3... n) and b rr =1 (r=1,2,3...m). Again, it is to be noted that a_pq=1/a_qp (p,q=1,2,3...n and p≠q) and b_rs=1/b_sr (r,s=1,2,3...m and r≠s).

Step 5: Calculation of Priority Vector (PV) values, largest Eigen values and consistency checking

Pair-wise comparison matrices are used to calculate priority vector values representing the relative priorities of: i) judgmental criteria with respect to goal and ii) alternatives with respect to each judgmental criterion. Priority vectors are normalized Eigen vectors. Among n number of judgmental criteria, w (w≤n) number of judgmental criteria having very high PV values compare to other judgmental criteria are selected as dominating and most effective judgmental criteria and are kept in a set called D. Only dominating judgmental criteria are used in AHP and non dominating ones are neglected. Calculation of PV values are shown in the following-

At first, sum of each column of pair-wise comparison matrices are calculated as per equation (1) and (2) –

JCCMat Co l sum __q

n

У a ;q = 1,2,3....n _pq;q , , ....

JCRACMat_y_Col_sum_i = ]T b_rs;y e D and s = 1,2,3...m   (2)

r = 1

JCCMat_Col_sum q and JCRACMat y _Col_sum s , calculatedin equation (1) and (2) respectively, denote the sum of q^th column of JCCMat and the sum of s^th column of JCRACMat y respectively.

Next, each relative importance value belonging to a column of a comparison matrix is divided by the sum value of that column (calculated as per equation (1) or (2)) for normalizing each relative importance value.

At last, PV values are calculated from the normalized relative importance values as per equation (3) and (4)- n

JCCMat_PV = (1/n) S (a_pq/JCCMat_Colsumq); ^p      q = 1

p = 1,2,3...n

JCRACMaty_PVr =

(1/m) S (b_rs / JCRACMat _y_Col sum _s) ’ ^{y e D and} s = 1

r = 1,2,3...m

JCCMat_PV p and JCRACMat y _PV r , calculated in equation (3) and (4) respectively, denote the PV value of JC p for JCCMat and PV value of A r with respect to JC y for JCRACMat y respectively .

Calculated PV values are used to calculate largest Eigen value. The calculation proceeds as per equation (5) and (6)- n

JCCMat_X_max = S JCCMat_Col_sum, * JCCMat_PV_p     ⁽⁵⁾

p = 1

m

JCRACMat_v X_max = I JCRACMat Col sum* JCRACMat_v PV_r y max               _y        r            y r

JCCM at λ    and JCRACMat λ , calculated in max             y max equation (5) and (6) respectively, denote largest Eigen value of JCCMat and JCRACMaty respectively.

Consistency checking is done by using Consistency Index (CI) and Consistency Ratio (CR). CI indicates the variation of consistency and calculated as per equation (7) and (8)-

JCCMat_CI = (JCCMat_ Я -n)/(n-1)         (7)

JCRACMat_y_CI = (JCRACMat_y_ ^ _max - m)/(m -1) (8)

JCCMat_CI and JCRACMat y _CI, calculated in equation (7) and (8) respectively, denote CI of JCCMat and JCRACMat y respectively.

CR is the ratio of CI and Random consistency Index (RI) and should be less than the acceptable threshold of 0.1(10%). RI of a comparison matrix is obtained as per the table developed by Saaty [1]. Table 4. shows the values of RI with respect to z (size of the comparison matrix).

Table 4. Values of RI with respect to size of comparison matrix

z	1	2	3	4	5	6	7	8	9	10
RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

CR is calculated as per equation (9) and (10)-

JCCMat_CR = JCCMat_CI/RI

JCRACMat CR = JCRACMat CI/RI y_y

JCCMat_CR and JCRACMat y _CR, calculated in equation (9) and (10) respectively, denote CR of JCCMat and JCRACMat y respectively.

Step 6: Calculation of composite Priority Weight (PW) values of each alternative from the PV values and ranking of alternatives

AHP needs to compute the modified priority weight values of dominating judgmental criteria in such a way, that the sum of these modified values is 1.0. Calculations of these modified values are shown as per equation (11)-

MPWJC _t = JCCMat PV / S JCCMat PV _v ; t e D t         _ t v e D       _ v

MPWJC t , calculated in equation (11), denotes the modified priority weight value of judgmental criterion JC t .

Now, the modified priority weight values of dominating judgmental criteria will be used to calculate the composite priority weight values of each alternative as per equation (12)-

CPWAlt _r= S (MPWJC _t* JCRACMat _t_PV_r); r=1,2....m t e D

CPWAlt r , calculated in equation (12), denotes the composite priority weight value of alternative A r .

Finally, the final CR value (F_CR) of the entire proposed hierarchy is calculated as per equation (13)-

F_CR = ((1 * JCCMat_CI) * S u e D

MPWJC *JCRACMat _CI)/((1*RI)* S MPWJC * RI) u e D

Finally, alternatives are ranked as per the descending order arrangement of their composite priority weight values.

• IV.    Experiment and Analysis

We have carried our experiment on 3 mobile phone alternatives namely M 1 , M 2 and M 3 representing A 1 , A 2 and A 3 respectively. So, we have m=3. AHP is applied on the alternatives using 3 judgmental criteria: Price (P), Battery Backup (BB) and Users’ Review (UR) representing JC 1 , JC 2 and JC 3 respectively. So, we have n=3. We have collected pair-wise comparison values from different buyers of mobile phones and formed pair-wise comparison matrices from those buyers’ inputs. AHP is applied on the comparison matrices and obtained results are kept. Our experiment shows that our proposed method produces a ranking of M1, M₂ and M₃ depending on input given by a buyer. This ranking helps the buyer to select the best suited mobile phone alternative for him or her. In the following, we are portraying results produced by AHP for a particular buyer’s input. Table 5. shows the JCCMat matrix, constructed from pair-wise comparison values given by a particular buyer.

Table 5. JCCMat matrix with buyer given pair-wise comparison values

P      BB     UR

P            1             93

BB           1/9           11/5

UR          1/3          51

Parameters defined in equation (1),(3),(5),(7) and (9) are calculated from JCCMat, shown in Table 5, in the following manner-

JCCMat_Col_sum 1 =1+1/9+1/3=1.444

JCCMat_Col_sum 2 =9+1+5=15

JCCMat_Col_sum 3 =3+1/5+1= 4.2

JCCMat_PV 1 =(1/1.444 + 9/15+3/4.2)/3 =0.6689

JCCMat_PV 2 =((1/9)/1.444+(1/15)+(1/5)/4.2)/3

=0.0637

JCCMat_PV 3 = ((1/3)/1.444+5/15+1/4.2)/3 =0.2674

JCCMat_λmax=1.444*0.6689+15*0.0637+4.2*0.2674 =3.0453

JCCMat_CI=(JCCMat_λmax – n)/(n – 1)=0.0227

JCCMat_CR=JCCMat_CI/RI=0.0391

It is observed that JCCMat_CR=0.0391<0.1, so consistency is maintained and calculation is acceptable.

Above calculations have produced an interesting result that JCCMat_PV2(0.0637) is very less compare to JCCMat_PV1(0.6689) and JCCMat_PV3(0.2674). This shows the absolute dominance of judgmental criteria P and UR over the judgmental criterion BB. So, P and UR are the most effective judgmental criteria. Thus, the use of BB in the subsequent calculations can easily be neglected without leaving any adverse effect. Hence, we have not considered BB in the subsequent calculations and have used pair-wise comparison matrices: JCRACMat1 (with respect to P) and JCRACMat3 (with respect to UR). Table 6. and Table 7. show JCRACMat1 matrix and JCRACMat3 matrix, constructed from pair-wise comparison values given by a particular buyer, respectively.

Table 6. JCRACMat 1 matrix with buyer given pair-wise comparison values

M1       M2M

M1          1          28

M2          1/2       17

M3           1/8      1/71

Table 7. JCRACMat 3 matrix with buyer given pair-wise comparison values

M1     M2

M1            1        1/51/6

M2          5       12

M3           6      1/21

Parameters defined in equation (2),(4),(6),(8) and (10) are calculated from JCRACMat 1 and JCRACMat 3 , shown in Table 6. and Table 7. respectively, in the following manner-

JCRACMat 1 _Col_sum 1 =1+1/2+1/8=1.625

JCRACMat 1 _Col_sum 2 =2+1+1/7=3.1429

JCRACMat 1 _Col_sum 3 =8+7+1=16

JCRACMat 1 _PV 1 =(1/1.625+2/3.1429+8/16)/3=0.5839

JCRACMat 1 _PV 2 =((1/2)/1.625+1/3.1429+7/16)/3

= 0.3545

JCRACMat 1 _PV 3 =((1/8)/1.625+(1/7)/3.1429+1/16)/3

=0.0616

JCRACMat 1 _λ max =1.625*0.5839+3.1429*0.3545+

16*0.0616=3.0486

JCRACMat 1 _CI=(JCRACMat 1 _λ max – m)/(m–1) =0.0243

JCRACMat1_CR=JCRACMat1_CI/RI=0.0419<0.1, ensures the consistency and acceptance of the calculation.

JCRACMat 3 _Col_sum 1 =1+5+6=12

JCRACMat 3 _Col_sum 2 =1/5+1+1/2=1.7

JCRACMat 3 _Col_sum 3 =1/6+2+1=3.1667

JCRACMat 3 _PV 1 =((1/12)+(1/5)/1.7+(1/6)/3.1667)/3 = 0.0845

JCRACMat 3 _PV 2 =(5/12+1/1.7+2/3.1667)/3=0.5455

JCRACMat 3 _PV 3 =(6/12+(1/2)/1.7+1/3.1667)/3=0.37 JCRACMat 3 _λ max =12*0.0845+1.7*0.5455+3.1667*.3 7=3.113

JCRACMat 3 _CI=(JCRACMat 3 _λ max –m)/(m–1)=0.056 5

JCRACMat 3 _CR= JCRACMat 3 _CI/RI=0.0974<0.1, ensures the consistency and acceptance of the calculation.

We have found two dominating judgmental criteria P and UR as stated earlier. Modified priority weight values of judgmental criterion P and UR are calculated from equation (11) in the following manner-

MPWJC 1 =0.6689/(0.6689+0.2674)=0.7144

MPWJC 3 =0.2674/(0.6689+0.2674)=0.2856

Composite priority weight values of mobile phone alternatives M1, M2 and M3 are calculated from equation (12) in the following manner-

CPWAlt 1 =(0.7144*0.5839) +(0.2856*0.0845)=0.4413

CPWAlt 2 =(0.7144*0.3545) +(0.2856*0.5455)=0.4090

CPWAlt 3 =(0.7144*0.0616) +(0.2856*0.37)=0.1497

F_CR is calculated from equation (13) in the following manner-

F_CR=((1*0.0227)+(0.7144*0.0243)+(0.2856*0.0565 ))                                                                            /

((1*0.58)+(0.7144*0.58)+(0.2856*0.58))=0.0485<0.1. So, the calculation of the entire proposed method is consistent and acceptable.

Now, descending order arrangement of CPWAlt r , r=1,2,3 values is- CPWAlt 1 > CPWAlt 2 > CPWAlt 3 .

The above arrangement makes the decision that mobile alternative M 1 is the highest ranked mobile phone and best suited for user. M 2 is the next highest ranked mobile phone and M 3 is the last ranked and worst suited alternative.

• V.    Conclusion

This paper tried to explore the problem of selecting the best suited mobile phone device by the ranking of the available device models from the choice domain of the buyers. The method is based on AHP with MCDM not yet explored for this specific purpose. The demonstration and effectiveness of the proposed method is carried out through case study. By application of the proposed method, e-commerce sites can offer a systematic numerical method for suitable mobile phone selection instead of qualitative one normally available now a day.

Buyers may get the rank list of device models with respect to judgmental priorities or criteria which may be a combination of specifications of the models. User level prioritization of mobile phone models is done based on some judgmental criteria. Our proposed work has successfully ranked mobile phones as per judgmental priorities and thus proves to be beneficial for the buyers in terms of providing an easy and time saving selection process. The proposed method may be improved by combining some sophisticated data mining techniques as well as fuzzy inference rules to evaluate priorities of products. The proposed method may also be extended for ranking other devices, project models and other products.