Mobile Robot Motion Using Cellular Automaton Model to Avoid Transient Obstacles

Published Online October 2013 in MECS DOI: 10.5815/ijmecs.2013.08.08

Path planning plays an important role in various fields of application and research. Many algorithms developed to assist the navigation of mobile agent, such as, people, robot, and other motion vehicle, in choosing the best path to their destination. A major goal in current mobile robotics research is to bring robots into natural human environments and also can safely carry out missions in populated environment. Though, in the worst case, the high-density environment may leave no free space for the robot to move.

This paper introduces path planning and obstacle avoidance motion for autonomously mobile robot. This simulation uses a typical corridor layout as a simulation environment and the pedestrian along the corridor was considered as the obstacles. Most of the current local path planning considers the obstacle in dynamic environment as moving obstacle. Moving obstacle means the velocity and direction of obstacle relatively constant and predictable [1] [2] [3]. However, this paper using different approach for the obstacle behavior. The pedestrian along the corridor was not threat as moving obstacle but as transient obstacle. Transient obstacle is obstacle with randomize velocity and arbitrary motion, hence, it can appears and disappears in the environment [4]. In the other word, the transient obstacle is timeindependent obstacle. Therefore, it is difficult to predict the further location of the robot based on its velocity and direction.

This paper presents the research and simulation result of local path planning using Cellular Automata model to avoid transient obstacle in dynamic environment. This paper also suggests the enhancement of local path planning with global path planning to eliminate the drawbacks of local path planning and to optimize the length of the path.

This paper is organized as follows. Some studies and theories relating with robot path planning issues and obstacles avoidance are quick reviewed in Section II and III. Cellular Automata model in robot path planning is presented in the Section IV. In the Section V, the proposed path planning model is described. Section VI contains the simulation process and results. Finally, in Section VII, we present the conclusion and the future works of this research.

• II.    Related Works

Research about robotic path planning covers a wide area because it enhances robotic navigation systems in both static and dynamic environment. There are exists a large number of methods for solving the basic path planning issues. Several traditional control methods have been applied, like certainty grid [5] a multidimensional representation of the robot environment. The space is subdivided into cells and a cell has a state. The state can be “free” or “occupied” depend on the object appearance. The other model are Potential Field and its improvement [6] [7] [8] represent a robot as a particle moving under the influence of an artificial potential field produced by the sum of a repulsive potential, generated by the obstacle, and a attractive potential, generated by the goal configuration. The artificial force pushes the robot away from obstacles and toward the destination as obstacle avoidance. Others are based on roadmaps [9] [10] in which a network of one-dimensional curves, called the roadmap, lying in the free space of the workspace is constructed. Another approach to local path planning is Vector Field Histogram (VFH) [11]. This method uses a two-dimensional Cartesian histogram grid as a world model. In order to compute the direction of vehicle then two-stage data reduction process is used. The first step reduces the map into one-dimensional discretized “polar obstacle density” function. In the second step, the algorithm selects the sector with a low polar obstacle density as the direction [12].

On the other hand, there are some local path planning methods developed to adapt and robust in dynamic environment. These methods react to the detected obstacles and change its heading direction in real time to avoid the obstacles. The example of local path planning method is Genetic Algorithm (GA) [13], which is developed from the idea of animal behaviors such as Ants Colony Optimization algorithm [14] [15] and algorithm from behavior of swarm such as Particle Swarm Optimization [14] [16].

• III.    Robot Path Planning and Obstacles Avoidance

The path planning problem is usually defined as follows [17]: “Given a robot and a description of an environment, plan a path between two specific locations. The path must be collision-free (feasible) and satisfy certain optimization criteria”. In other words, path planning is generating a collision-free path in an environment with obstacles and optimizing it with respect to some criteria (such as shortest routes, least energy consuming or shortest time) with collision free.

In order to plan a collision-free path for a mobile robot, path planning is divided in two main types of method: global path planning and local path planning. Global path planning requires the situation of robot workspace to be completely known in advance and the characteristic of obstacles should be static. In this section, the algorithm generates the complete path from robot’s start point to goal point before the first motion of the robot. While in local path planning approach, the path planning is done while the robot is moving. In other words, the algorithm is capable of producing a new path in response to environmental changes [17].

Most of the research about obstacle avoidance distinguishes obstacles based on its motion character: static obstacle and moving obstacle. Static obstacle means the position of the obstacles is always fixed. On the contrary, moving obstacle is able to move with their constant and predictable velocity. These two characters of obstacle have an impact on their environmental situation, i.e. static or known environment and dynamic or unknown environment.

One of the main concerns of the global path planning is to find a globally optimal path from robot’s current position to target location. This global path planning typically ignores moving obstacles. In contrast, local path planning algorithms in dynamic environment do not attempt to optimize the length of a path. Local path planning just concerns about moving obstacles avoidance that is ignored by global path planning. Therefore, both types of method have their shortcomings in dynamic environments. Global path planning produces slower response to unforeseen obstacles and required a re-planning of the path while the environment changes [18] [19]. Although the local path planning methods are very suitable in dynamic environment, they also have their drawbacks. The robot can get trapped in local minima [20], can be pushed away by a moving obstacle and never reach the destination, which is called “blockade” [18], and local path planning methods seems inefficient when the goal is far away and the environment is cluttered.

• IV.    CA Model in Robot Motion

The proposed method is based on Cellular Automata (CA) model [22]. The usages of CA model as simulation-based tool are widely used in a great variety of domains, from statistical physics to social science. CA can be used as a model tool for application where the parallel treatment and the local interaction became relevant. In this paper, CA has been used to solve the local path planning problem in dynamic environment for a mobile robot to avoid collision with transient obstacles.

The CA model consists of two components. The first one is a cellular space, that is a regular lattice of cells, where are situated in a grid and with the same finite machine in each node. Every node of a graph is represented as a point of the space Z ^k, where k is dimensional space of integer number.

A Cellular Space is a graph G= ( Z ^k, A) where the arcs set:

A c z^k x Z^k                               (1 )

is invariant for translations. For example, if we have the arc:

( j, i ) e A ^ ( j + 5 ,? + r e A              ^{(2 )}

In particular, with j = 0, where j is the node in the origin of the coordinates system, the expression is reduced to the form:

A n = n + A , V n e Z^k                 (3)

This relation means that it is possible to deduce the topology structure of the whole space just knowing the neighborhood of the node 0. Refer to eq. (3), the cellular space can be defined simple as:

G = ( Z k , A ,)                              (4)

The second one of CA components is a set of state Q. In the set of states Q there is a state called 0 that represents the quiescent state f (0, 0, . . ., 0) = 0. If a cell is in the state 0 as all the neighbor cells, then the state does not change. Generally the quiescent state is unstable, because it is sufficient to change a neighbor node’s state to evolve to different states. There are at least two kinds of topologies in a bi-dimensional space: the von Neumann neighborhood (A0 = {(l,0), (-l,0), (0,0), (0,l), (0,-1)}) and the Moore neighborhood (A0 = {(1,0), (-1,0), (0,0), (0,l), (0,-l), (1,l), (1,-l), (-1,1), (-1,1)}). Fig. 1 shows von Neumann and Moore topologies model with arrows indicating the direction of movement. Hence, a Cellular Automata is defined as quadruples Л = (Z^k , Л д , Q, f (•)), where:

• •    Z^k is a k dimensional space of integer number;

• •    Л₀ is the set of arcs connecting the origin node to its neighbors;

• •    Q is the set of states;

• •    f (•) : Q^⁰ ' ^ Q is the transition function of

each node.

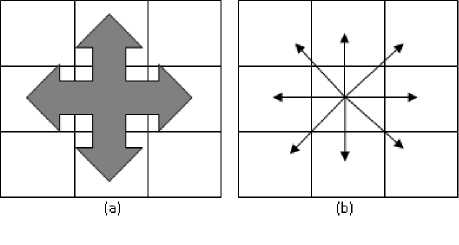
Figure 1. Von Neumann (a) and Moore (b) local neighborhoods.

• V.    Hierarchical Navigation Model

This paper uses grid model to present the environment of the mobile robot. In grid map, the workspace of robot will be divided into cells. Each of the cells is associated with Cartesian coordination. A cell may be a home to two kinds of object:

• a)    The robot (represented by black rectangle).

• b)    The   pedestrian   as transient obstacle

• 5.1    Representation of the Pedestrian Model and Environment

(represented by red and blue circles).

If a certain cell is occupied by robot or pedestrian, then we call it an occupied cell. If a certain cell is not occupied then it is a free cell. A scene of a typical corridor has been created and assuming that the space in which a robot moves is a limited region with transient obstacles. Fig. 2 illustrates an environment, which exhibits a certain configuration.

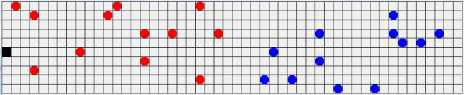
Figure 2. An environment with a certain configuration.

The model use two-dimensional system. A simple layout corridor was used as the simulation environment. The underlying structure is a W xW grid cell, where W is the system size. Each cell can either be empty or occupied by exactly one pedestrian as transient obstacles. The size of a cell corresponds to approximately 0.4 m × 0.4 m. This is the typical space occupied by a pedestrian in a dense crowd [23]. The transition update is synchronous for all pedestrians. Empirically, the average velocity of a pedestrian is about 1 ms^-1 under normal [24]. So, one time-step to closest cell in this model is approximately 0.4 s.

This paper uses the von Neumann neighborhood as the rule of state topologies model. This rule defines the state of a cell in dependence of the neighborhood. The state of a cell at the next time-step t + 1 is dependent on the states of the cell above, cell below, cell right, cell left, and the core cell itself. However, as mentioned before this paper consider the pedestrian as transient obstacles, so in a set of pedestrian P 1 , P₂,..., P , , each pedestrian P , exist in the scene for a certain interval of time [t 1 , t₂ ], where t 1 < t₂. This time interval is called P , ’s existing period in this paper.

In order to become transient obstacles, this simulation model applies velocity parameters for the pedestrian. The velocity of pedestrian is P J = [0 : v_max ] . These parameters have the sense that each pedestrian can expand the chance to increase their walking velocity from zero to maximum velocity v_max . The pedestrian motion is defined by the equation P t = P t (t) + [0 : v_max ] , where P_t (t) is the velocity of the pedestrian by the time t.

In the model, there are two components of pedestrian including the right pedestrian moving from the right to the left boundary and the left pedestrian moving from the left to the right boundary. The periodic boundary conditions are adopted, that is, if the right pedestrian arrives on the left boundary, he moves to the right boundary, if the left pedestrian arrives on the right boundary, he moves to the left boundary. The right or left pedestrian can also move out of the upper (or bottom) boundary and get into the bottom (or upper) if necessary. Thus, the total number of pedestrian among corridor is always constant. As the transient obstacle then the pedestrian in this model have two main characters, arbitrary motion and randomize velocity. Fig. 3 shows all the possible configurations of the left pedestrian in the core cell may encounter.

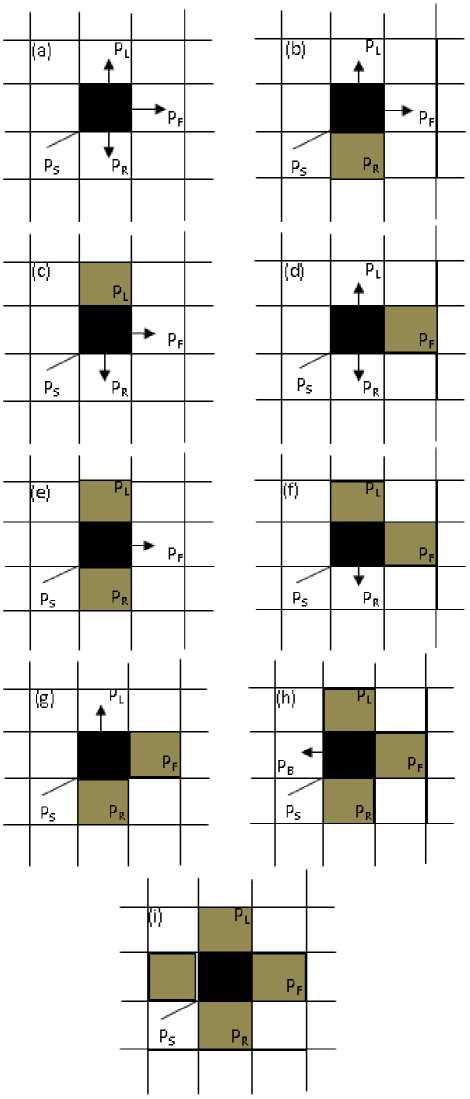
Figure 3. All the possible configurations of the left pedestrian.

The arrow in the core cell indicates the possible direction of the left pedestrian may select. In Fig. 3, PF, PL, PR, PB, and Ps represents the probability of chosen the direction forward, left side, right side, backward, and stationary (motionless), respectively. Then, it assumed that PF + PL + PR + PB + Ps = 1. For example, in Fig. 3.a, there are four transition probabilities that left pedestrian may select if cell right, cell left, and frontcell are unoccupied: move forward PF, move left PL, move right PR, and stationary (motionless) Ps. For Fig. 3.h, there is a special case in this model. If left cell, right cell, and front cell are occupied then the pedestrian can make a back stepping. Then, the probability of selecting the back cell or stationary is PB and Ps respectively. Otherwise, if all the neighborhood cells are occupied, such pedestrian has to steady in core cell at time-step.

The similar treatment is defined for right pedestrian. However, as the consequences of the rule that one cell can only be occupied by one pedestrian at a time-step then in the situation that there is more than one pedestrian vies for a cell, only one of them will be chosen randomly. The other one have to wait at this time-step.

• 5.2    Robot Local Path Planning – Cellular Automata Model

In this approach, a mobile robot without dynamic and kinematic constraint is considered. The dynamic properties of the robot are ignored and the problem is transformed to a purely geometrical path-planning problem. This model consider the robot as a point, occupies exactly one cell in a grid model. Given a start time t o , our problem is to determine a local path planning for a robot to avoid collision with pedestrian. Since the pedestrian is a transient obstacle, it is difficult to predict the location of pedestrian at next time-step just by using the information of obstacle’s speed and direction.

Instead of using common prediction method, this paper uses the simple local Cellular Automata transition rules for robot to avoid the collision with pedestrian. Similar with the CA model applied for pedestrian, this robot uses the von Neumann neighborhood to react against pedestrian around its location. The robot can move only one cell per time-step.

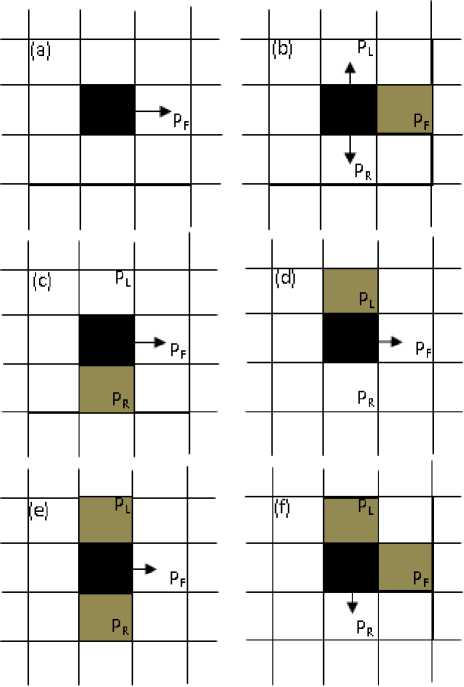
To cope with the collision probability between the robot and pedestrian, this paper proposes and compares two types of robot’s motion strategy by using CA model. The first one is “stop and go” method. In this method, assume the global path between robot start point to destination point have been determined without consider about the location of pedestrian. The robot is required to navigate through a corridor from start point to the destination point. When the robot encounter transient obstacle at front cell, it will wait until the front cell is a free cell then move again until reach the destination. Fig. 4 shows the configurations of this method.

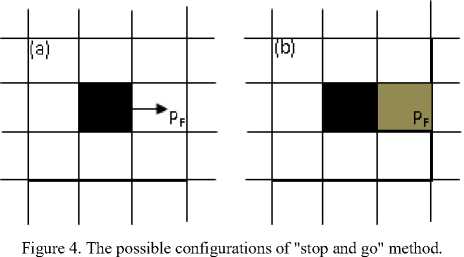
In this method the velocity for robot is an integer value between zero and v_max . Refer to fig. 4.a, if the front cell of the robot is unoccupied, the robot may select the cell to move and no matter if its left and/or right cell is occupied or not. However, illustrated by Fig. 4.b, if the front cell is occupied then the robot will stop.

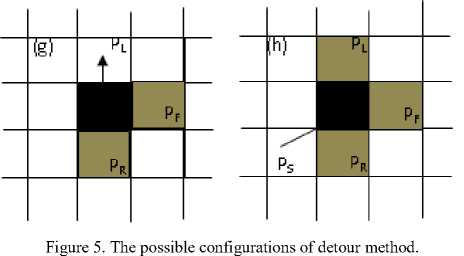
The second strategy for robot to avoid transient obstacle is detour method. In this method, assume the global path between robot start point to destination point have been determined without consider about the location of pedestrian. The robot is required to navigate through a corridor from start point to the destination point. From start point, if the front cell of the robot is unoccupied, the robot may select the cell to move. Otherwise, if the robot encounters transient obstacle at front cell then it will make a detour motion to avoid the transient obstacle. Fig. 5 shows the all configurations of this strategy.

In the detour method, the robot always select to move to front cell as far as it is an unoccupied cell. For the situation illustrated in Fig. 5.b, the probability of selecting the left cell or the right cell is P_L and P_R respectively. Refer to Fig. 5.h, if left cell, right cell, and front cell are occupied then the robot has to steady in core cell at this time-step.

• VI.    Simulation and Results

In the initial stage, the two-dimensional typical corridor has been created. The corridor size was 50x10 cells. The map represented robot start point and the destination point. The left and right pedestrians were distributed randomly. The density of each kind of pedestrian was p/2. The total density was defined as the number of total pedestrian divided by the total number of cells. The minimum velocity of pedestrian was zero and v_max = 1 cell/time-step. All the cells’ states were parallel updated. Fig. 2 shows the initial map of this simulation.

This simulation have applied and evaluated two types of robot’s motion strategy, “stop and go” method and detour method. This simulation analyzed the travel time and the mileage of robot to reach the destination area. The numbers of obstacles have been arranged in such a way that increases the density. Before the robot’s first time moving, we assumed the global path planning have been determined. This simulation used Dijkstra shortest path to generate the shortest route between start-point to destination point without consider about pedestrian locations. Fig. 6 illustrates the initial state while global path already determined.

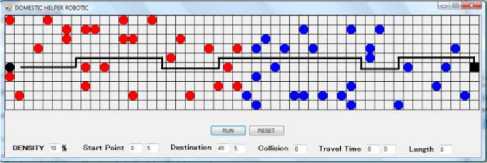
Figure 6. Initial state with global path planning.

Fig. 7 and Fig. 8 illustrate the robot’s motion strategy in order to avoid collision with pedestrian by using “stop and go” method and detour method, respectively.

To avoid the local minima problem of using detour method, we also improved this method. This improved method useful to keep maintains the position of robot to stay in global path after make a detour motion. This method uses number to give a value on the global path. The farther the distance of a cell from the global path then the greater its value.

----COLLISION

----TIME(s)

Density (%)

Figure 7. Stop and Go method.

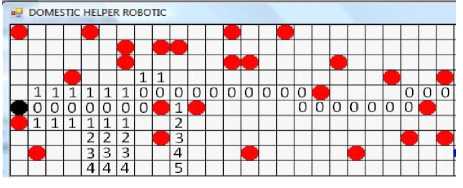
Figure 8. Detour method.

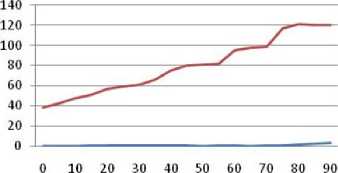
In the travel time analysis, Fig. 9 and Fig. 10 show the robot travel time from its start point to destination point by using “stop and go” method and detour method, respectively. The red line illustrates the robot’s travel time and the blue line is the number of collision that occurred between robot and pedestrian. Fig. 10 shows that the detour method has a minimum travel time rather than using “stop and go” method. While in Fig. 11, the comparison result of path length between these two methods shows that the “stop and go” method produce shortest-distance path for robot to reach its destination while avoid the collision with pedestrian. These results confirmed that “stop and go” method, as the Djikstra-improved based method, is not flexible to produce an effective time-path among dynamic environment. However, because this “stop-and-go” method based on Dijsktra algorithm then it keeps maintained its path as the shortest one.

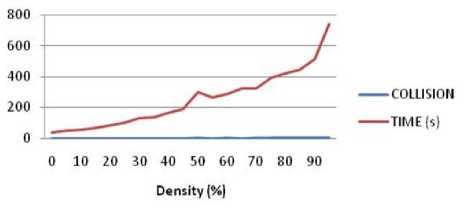
Figure 9. Travel time using "stop and go" method.

Figure 10. Travel time using detour method.

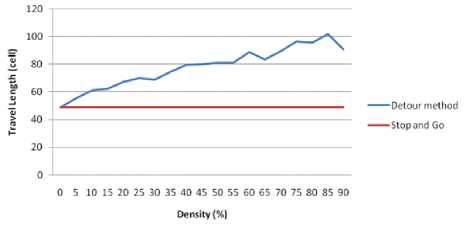
Figure 11. Distance needed by the robot to reach the goal.

• VII.    Conclusion and Future Work

This paper presents the problem of mobile robot path planning in the presence of transient obstacles. A simple Cellular Automata model has used to cope with the collision probability between the robot and pedestrian as transient obstacle along the corridor. This paper proposes two types of robot’s motion strategy to avoid the transient obstacles: “stop and go” and detour method. The simulation results show that in dynamic environment that having transient obstacles, the “stop and go” method produced minimal collision with shortest-distance path. While, the detour method generated minimum collision with time-minimum navigation path. Those means that using “stop and go” method, the robot only need a minimum resources to reach its destination rather than using detour method. On the other hand, for time minimum oriented of mobile robot, the detour method produced better path planning than “stop and go” method.

Future work includes incorporating another type of obstacles and using more complex working environment as the representation of real environment. Hence, we need to analyze when the appropriate situation for the robot to choose between using “stop and go” method and detour method to reach the optimal path.