Модальное управление асинхронным электроприводом тележки мостового крана с наблюдающим устройством

В качестве грузоподъемных механизмов на промышленных предприятиях широко используют мостовые краны. При перемещении тележки и моста крана неизбежно возникает раскачивание подвешенного груза. Около 20 % времени полного цикла перегрузочных операций затрачивается на ожидание завершения колебаний груза, что существенно снижает производительность и усложняет работу оператора. Кроме того, раскачивание груза приводит к увеличению динамических нагрузок на приводы и металлические конструкции крана [1].

В данной статье рассматривается способ подавления колебаний груза при помощи модального управления электроприводом перемещения тележки мостового крана с использованием наблюдателя. Определение структуры системы автоматического управления скоростью груза рассматривается как двухэтапный процесс. На первом этапе синтезируется модальный регулятор в предположении, что все переменные состояния системы доступны измерению. На втором – синтезируется и включается в структуру системы наблюдатель переменных труднодоступных непосредственному контролю.

Синтез модального регулятора

Для конкретности в качестве объекта исследования выберем электропривод перемещения тележки мостового крана с подвешенным грузом, однако всё изложенное справедливо и для электроприводов перемещения моста и подъёма груза.

БК              АД

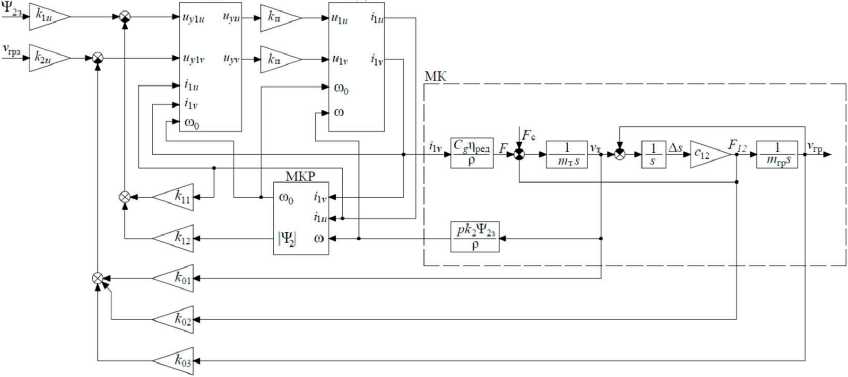
Рис. 1. Структурная схема электропривода перемещения тележки с грузом с модальным управлением

Fig. 1. Block diagram of an electric drive for moving a truck with a load with modal control

Структурная схема системы автоматического управления скоростью перемещения груза (рис. 1) составлена в предположении, что все переменные состояния объекта исследования доступны измерению. В основе этой структурной схемы лежит структурная схема системы векторного частотного управления скоростью асинхронного двигателя с модальным регулятором, рассмотренная в [2].

На рис. 1 блоки АД, БК, МКР – это структурные схемы асинхронного двигателя (АД) (в переменных I 2 -Ψ 2 ), блока компенсации внутренних перекрестных связей структурной схемы АД и, соответственно, структурная схема электромагнитного контура ротора (см. [2, 3]).

Коэффициенты обратных связей k 11 , k 12 и k 01 , k 02 , k 03 в совокупности с соответствующими сумматорами и узлами сравнения образуют двухканальный модальный регулятор. Первый канал ( k 11 , k 12 ) обеспечивает стабилизацию потокосцепления ротора АД, а второй ( k 01 , k 02 , k 03 ) – формирует диаграмму скорости перемещения груза ν _гр . Коэффициенты k _{1 u} и k _{2 u} согласуют сигналы задания потокосцепления ротора Ψ 2з и скорости перемещения груза ν грз с их реальными выходными значениями Ψ ₂ и ν _гр . Преобразователь частоты по каждому из каналов управления учтён безынерционным звеном с коэффициентом передачи k п .

Механическая часть объекта управления, которая состоит из тележки с приведенной к валу двигателя массой m т и груза массой m гр , подвешенного на канате длиной h , на рис. 1 представлена структурной схемой (блок МК) двухмассовой системы с упругой связью [4].

Здесь C_g = Ърк^_т11 – коэффициент связи электромагнитного момента с координатой i 1ν вектора тока статора АД; p , k ₂ – число пар полюсов АД и коэффициент электромагнитной связи ротора; η ред – КПД редуктора; ρ – радиус приведения угловой скорости двигателя к линейной скорости тележки; с ₁₂ – коэффициент упругой механической связи между массами тележки и груза; ν т – скорость перемещения тележки; ν гр – скорость груза; F c – cила, препятствующая передвижению тележки с грузом; F ₁₂ – сила, прикладываемая к грузу при его отклонении от вертикального положения; ∆ s – отклонение груза от вертикального положения.

Поскольку структурная схема объекта управления на рис. 1 отличается от рассмотренной в [2] только структурой механической части МК, то структура и процедура синтеза модального регулятора по каналу стабилизации потокосцепления Т ₂ ротора АД идентичны рассмотренным в [2] и в настоящей работе не рассматриваются.

Канал же формирования скорости перемещения груза ν _гр отличается как структурой, так и набором переменных состояния. Рассмотрим синтез модального регулятора для этого канала.

Для рассматриваемого класса механизмов инерционность электромагнитных контуров АД многократно меньше инерционности механической части системы, поэтому представляется правильным на этапе синтеза ею пренебречь. Тогда объект управления описывается следующей системой уравнений состояния [4]:

^^Vt dt

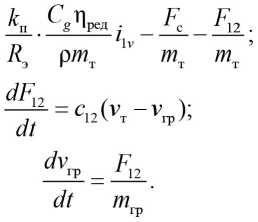
Этим уравнениям соответствуют матрицы параметров А и входа В:

	^^п	<7[2	w13		0	1_ 7ИТ
							0
А =	^21	Я22	^23	=	С12	0	-С12	и В =	^21
	<^31	^32	^33 у		0	1	0		^^31>

Тогда, с учётом структуры модального регулятора скорости груза v _гр (см. рис. 1), характеристический полином замкнутой по вектору состояния системы определяется выражением [5]:

д(5) = |5-£-Ц-5-^)|

где                  – матричный коэффициент модального регулятора; E – единичная матрица.

С учётом (1) выражение (2) равно:

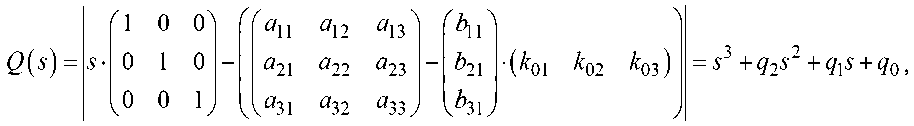
^ОХ^п^^Лред      ^02 С12 ^11 (-g Пред с12(^гр ^т)      (^03 ^01 )с12^"п^ ^Пред

где

Аэрт_т          К^т^       т^т^           К^рт^т^

Выбрав в качестве желаемого характеристический полином фильтра Баттерворта третьего порядка

D^ — -У + 2со^5 + Зоэ^^ + со^

обеспечивающий перерегулирование σ = 7,1 % и время переходного процесса τ _пп = 5,9ω _б ^-1[5], и приравняв его к уравнению (3), определим коэффициенты модального регулятора:

la^Rpm    ^эР^Юб^т-^^-^тЯ

^oi = , _г     ; ^02 = —^к-------- 77-----------;

^п^^Лред                ^rp^lZ^n^g^pefl

R₃pm_Tto₆ I w_rp(o₆ + 2с₁₂ I

Для численных расчётов использованы параметры АД RA 250 M 2 ( P н = 55 кВт, n н = 2950 об/ мин). Приведенная масса тележки, масса груза и длина каната приняты равными: m _т = 133,5 т; m гр = 150 т; h = 30 м. Базовая частота, определяющая быстродействие системы, выбрана из условия ограничения бросков переменных состояния на допустимом уровне: ω _б = 1,18 с^-1. При этом численные значения коэффициентов модального регулятора: k 01 = 0,135; k 02 = 2,45 ∙ 10^–6; k 03 = 0,153.

Графики изменения скорости груза ν гр и скорости тележки ν т при Ψ 2 = const и ступенчатом задании ν _грз приведены на рис. 2.

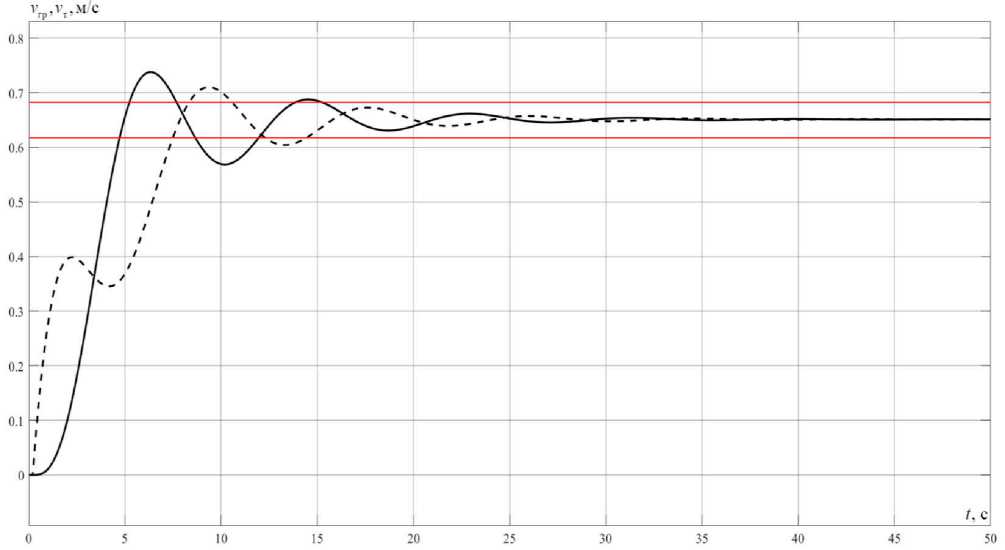
Рис. 2. Переходные процессы скорости груза и тележки (где сплошная линия – скорость груза νгр, пунктирная – скорость тележки νт)

Fig. 2. Transients of the speed of the load and the trolley (where the solid line is the speed of the load ν гр , the dotted line is the speed of the trolley ν т )

Как видно, рассматриваемая система автоматического управления скоростью перемещения груза обеспечивает переходный процесс, близкий к желаемому ( t _пп = 15 c, σ _гр = 13,19 %), кардинально устраняя при этом его колебательность – для сравнения можно взять результаты работы [6].

Синтез наблюдающего устройства

Синтез модального регулятора осуществлён в предположении, что все переменные состояния системы доступны измерению (наблюдаемы), однако сила F ₁₂ и скорость пере -мещения груза ν гр таковыми не являются. Поэтому определим их с помощью наблюдающего устройства (НУ).

В самом общем случае математическая модель наблюдателя в векторно-матричной форме имеет вид [5]:

Х(0 = ЛХ(0 + BU(0 + G(Y^ - СХ(^ .                        (4)

Здесь переменные Х(Л - это переменные, определяемые наблюдателем; Y ( t ) - переменные, доступные измерению; U ( t ) - входные переменные объекта; A - матрица параметров объекта; B - матрица входов объекта; C - матрица размерности ( r х n ) выходов объекта, доступных измерению; G – матрица размерности (n×r) коэффициентов регулятора НУ.

Уравнение (4) в операторной форме имеет вид:

sX^ =(Л- GC)X(s) + BU(s) + G(Y(s)) .

Ему соответствует характеристический полином:

7V(5) = |s£-(^-GC)|.

При синтезе НУ будем считать известным задающий сигнал uyv напряжения на входе преобразователя и доступным измерению сигнал скорости перемещения тележки у _т .

Переменные, не доступные измерению и определяемые наблюдателем: проекция тока статора i 1 v , сила, прикладываемая к грузу при его отклонении от вертикального положения, F ₁₂ и скорость перемещения груза v _гр .

Тогда, согласно [2, 3] и структурной схеме рис. 1 системы автоматического управления, уравнения наблюдателя в скалярной форме будут иметь вид:

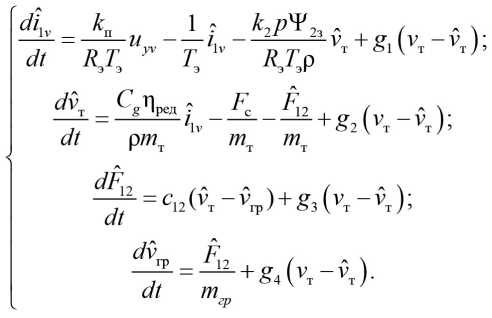
Отметим, что здесь в модели объекта наблюдения учтена и электромагнитная инерция обмоток АД.

Таким образом, для рассматриваемого объекта матрица-столбец коэффициентов наблюдателя равна:

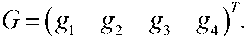
Матрица-строка переменных, доступных измерению:

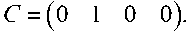
Матрица динамики:

		М^з	0	> 0
	Т3	RJ3^
о        а а			1
а^,                аэ.	g *ред	0		0
А =                =	pm^		/ит
а31 а„ а„ а34
	0	А 2	0	—Аг
^41  ^42  w43  ^44/			।
	0	0		0
	V		П1гр	2

Характеристический полином НУ определяется выражением:

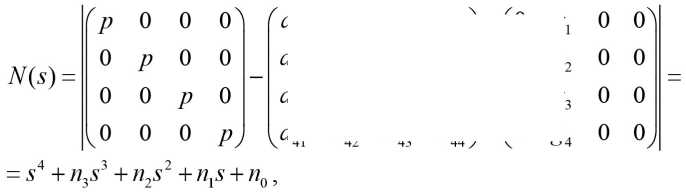
1 .      ft ^g Пред §2 ft A2(^wt + ftp) ^Р’^^з^Пред

Ai	ft 2	ft3	ft4^		'0	gl
^21	а22	а23	ti24	+	0	§2
fti	ft 2	ft3	ft 4		0	ft
а41	ft2	O43	ft4>		<°	ft

где

4       pm_T Г_э m_T m^^ R₃I₃p^zm_T

„ - ft£12 ft , ft£12 , A2^Ap ^+mr) .   _ РПАг^Пред ftA2 , ft^c12 , ^Р^гз^ хПредАг

/ftp ^Тэ^тт ^mT T₃m_rpm_T         pm_Tm_Tp T^ T₃m_T R₃I₃p-m_Tm_rp

Выбрав в качестве желаемого характеристический полином четвертого порядка c настройкой на модульный оптимум:

D(s) = s⁴ + 2, 82co₆s³ + 4сОб^² + 2,82ш^ + cog , обеспечивающий перерегулирование о = 6,2 % и время переходного процесса т _пп = 7ю _б ^-1 [5], и приравняв его полиному N ( 5 ), определим коэффициенты матрицы G наблюдающего устройства:

ft =

ft =

Т⁴(4-2ЖУб^^тУб-2Ж^^                  1

------------------------------, ft = 2,82(ofi--;

anT^y3)                 6 Тэ’

Г з со £ -2,82Г_эсо б -4Г ² со ^ Q^ + 2, 82P₃g)₆Q^ + П² (1 + Q²_p7 ^

4«>б+2,82Г2(Об^2

ft =-----------------

(l + Q^72)/mT

-4Гэю^^ -2,82Г;юбО^ + 7^

Q2(1 + Q^P2)

где                и               – резонансные частоты груза и тележки;            ;

и                 – коэффициенты матрицы динамики А (5).

Структурная схема синтезированного НУ приведена на рис. 3.

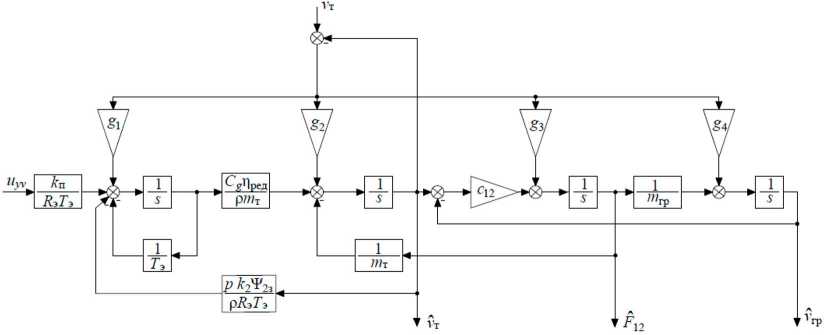
Рис. 3. Структурная схема синтезированного наблюдающего устройства

Fig. 3. Structural diagram of the synthesized observing device

Для наблюдателя значение ω _б ограничивается только условиями помехозащищённости системы, поэтому для численных расчётов принимаем ω б = 100 с^-1. Тогда g 1 = 3,14 ∙ 10⁵; g 2 = –1,114; g 3 = –8,315 ∙ 10⁵; g 4 = 224,537.

Графики изменения скорости тележки и скорости груза в системе с наблюдателем представлены на рис. 4 и рис. 5 соответственно.

Как видно из графиков, максимальная погрешность определения V^ наблюдается на начальном этапе процесса, но она никак не влияет на процесс перемещения груза в целом. Про-

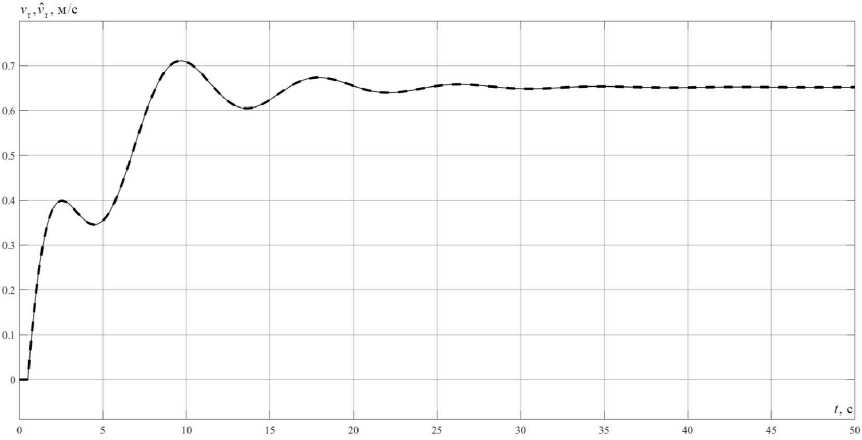
Рис. 4. Графики изменения скорости тележки (сплошная линия – скорость тележки V определяемая наблюдателем, пунктирная – реальная скорость тележки ν т )

Fig. 4. Graphs of the trolley speed change (solid line – the trolley speed VT determined by the observer, dotted line – the real trolley speed νт)

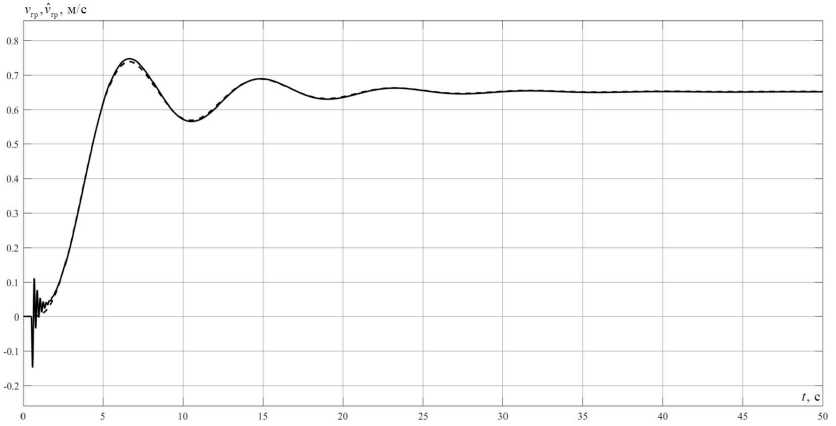
Рис. 5. Графики изменения скорости груза (сплошная линия – скорость груза V^, определяемая наблюдателем, пунктирная – реальная скорость груза νгр)

Fig. 5. Graphs of changes in speed of the load (solid line – the speed of the load V^ determined by the observer, dotted line – the real speed of the load νгр)

цессы в замкнутой системе электропривода с НУ полностью совпадают с процессами в системе, построенной в предположении, что все переменные наблюдаемы (см. рис. 2).

Таким образом, предлагаемая система модального управления асинхронным электроприводом тележки мостового крана с использованием наблюдающего устройства позволяет решить проблему подавления колебаний подвешенного груза.

Для реализации предлагаемого наблюдателя требуется четыре интегратора и несколько усилителей. Он легко реализуется как аналоговыми, так и цифровыми электронными средствами. Достоинством такого наблюдателя является то, что он позволяет полностью оценить вектор переменных состояния электропривода.