Модальный анализ и динамические характеристики мачтовых конструкций с дефектами и повреждениями

Модальный анализ, предполагающий установление основных динамических характеристик (частот и форм собственных колебаний), является важнейшим элементом проектных расчетов мачтовых конструкций. Это связано с тем, что один из линейных размеров (высота), как правило, намного превышает размеры сооружения в плане, что, в свою очередь, приводит к низкой его жесткости в горизонтальной плоскости и возможности возникновения больших амплитуд колебаний при действии ветровых и сейсмических воздействий. С этим связаны опасности как возникновения резонансных явлений и разрушений мачт, так и нарушения работоспособности технологического оборудования телерадиовещания и связи.

Исследование динамических характеристик несущих конструкций аналитическими методами с достаточной точностью возможно для достаточно простых технических объектов, для которых обосновано использование расчетной схемы, представляющей собой сосредоточенную массу на стержневой опоре. В других случаях возникает необходимость использования численных, преимущественно конечно-элементных, методов анализа.

Расчет свободных колебаний методом конечных элементов осуществляется на базе дифференциального уравнения свободных колебаний

[ M ] {*} + [ K ] { x } = 0, являющегося частным случаем общего уравнения движения

[ M ]{*}+[ C ]{x}+[ K ]{x }=0, где [M], [C], [K] – матрицы масс, демпфирования, жесткости конструкции, дискретизированной как система конечных элементов; {x}, {.x}, {x} - векторы ускорений, скоростей и перемещений узлов конечноэлементной модели.

В анализе свободных колебаний предполагается упругое поведение конструкции, поэтому ожидаемый отклик является гармоническим:

{ x } = { ф i } cos ( to t ) , где ф i - собственный вектор, определяющий форму колебаний i -й моды (тона); ω _i – собственная частота этой моды.

Подстановкой второго уравнения в первое получаем

• -to ² [ M ] { ф _z } cos ( m _zt ) + [ K ] { ф _/ } cos ( ю/ ) = 0 , (^- ® 2 [ M ] + [ K ] ) { ф / } ^cos ( to t ) = ⁰ .

Собственные частоты находятся из уравнения

([ K ]-»2 [ M ])(ф,)= 0.

Этот широко распространенный и реализуемый в пакетах конечно-элементного анализа алгоритм основан на следующих допущениях:

• 1.    Предполагается линейное упругое поведение материалов, эффекты демпфирования и диссипации энергии не учитываются.

• 2.    Предполагается линейное поведение конструкции, структурные нелинейности не учитываются.

Таким образом, модальный анализ выполняется для физически и структурно линейных систем. Вместе с тем, мачты на оттяжках являются специфическими объектами проектирования и расчета, которые характеризуются следующими особенностями [1]:

– нелинейной работой вантовых элементов-оттяжек;

– необходимостью задания усилий предварительного напряжения;

– необходимостью учета «эффекта силы, направленной в полюс» при передаче усилий от оттяжки на ствол;

– критичностью проверок устойчивости равновесия ствола.

Указанные факторы, обусловленные наличием предварительно напряженных оттяжек, воспринимающих только растягивающие усилия, приводят к нелинейному характеру деформирования мачтовых систем.

В связи с этим для выполнения модального анализа мачт с оттяжками, являющихся структурно нелинейными конструкциями, необходимо построение линеаризованной системы, т. е. рассмотрение конструкции, работающей в геометрически линейной постановке, но учитывающей достигнутый уровень усилий в оттяжках в состоянии, предшествующем линеаризации, а также достигнутый уровень усилий сжатия в соответствующих сжатых элементах расчетной схемы.

Точнее говоря, под линеаризованной системой понимается исходная система, в которой все составляющие ее элементы рассматриваются в линейной постановке, но с касательными (мгновенными) матрицами жесткости. Для линеаризации системы и выполнения ее модального анализа могут быть использованы следующие теоретические предпосылки и алгоритм [2].

С позиций строительной механики оттяжки мачт являются вантовыми элементами, порождающими, как гибкие нити, геометрически нелинейные эффекты. В качестве расчетной модели вантового элемента принята гибкая нить с малой стрелкой провисания, которая в исходном состоянии, характеризуемом температурой T0 и натяжением H0, нагружена поперечной нагрузкой q0(x) и у которой при удлинении хорды на ∆ и изменении поперечной нагрузки до величины q(x), а температуры до T натяжение становится равным H.

Уравнение состояния вантового элемента, связывающее эти величины, для пологих нитей имеет вид

_A = ( H — H о ) L

EA

D^ + - D - + а ( T - T ) L , 2 H ² 2 H ₀ ^{2         0}

где

LL

D = J Q 2 ( x ) dx , D о = j Q 02 ( x ) dx , 00

где Q ( x ) – поперечная сила, возникающая в шарнирно опертой балке пролета L от действия нагрузки q ( x ), направленной поперек хорды вантового элемента; Q ₀( x ) – то же, но от нагрузки q ₀( x ); α – коэффициент температурного расширения; E – модуль упругости материала нити; A – площадь поперечного сечения нити.

Мгновенная податливость вантового элемента в окрестности некоторого напряженного состояния, характеризуемого натяжением H , определяется дифференцированием уравнения состояния:

d A   L  D

------=--1--5- . dH EA H ³

В тех случаях, когда единственной распределенной поперечной нагрузкой на элементе является собственный вес нити, из последнего выражения получается известная формула для определения площади A ₀ условного стержня той же длины L , жесткость которого при продольных деформациях совпадает с мгновенной жесткостью нити:

A

0 = A

"^5ё

12 g ³

где ρ – объемный вес материала нити; l – длина горизонтальной проекции нити; σ = H/A – осевое напря- жение в нити.

Все эти рассуждения имеют смысл только при весьма малых значениях δ = ∆/ L (порядка 10^–3–10^–2), при которых справедливо уравнение состояния.

В настоящее время накоплен значительный опыт применения описанных методических подходов (численного модального анализа линейных деформируемых систем и линеаризации мачт на оттяжках), что является предпосылкой получения достоверных результатов модального конечно-элементного анализа таких конструкций. Новизна постановки задачи заключается в выполнении модального анализа конструкций мачт, как соответствующих проектным характеристикам, так и содержащих дефекты и повреждения, полученные в процессе монтажа и эксплуатации. Актуальность такой постановки задачи обусловлена тем, что поврежденная конструкция имеет другие динамические характеристики. Это, в свою очередь, меняет условия достижения резонанса, а также меняет условия нагружения при неизменных внешних физических воздействиях, поскольку в соответствии с действующими нормативами [3; 4] эти физические воздействия трансформируются в эквивалентные силовые факторы, величина которых непосредственно связана со значениями частот первых форм собственных колебаний.

Исследование закономерностей формирования динамических характеристик мачт выполнено на примере мачтовой конструкции высотой 21 м, состоящей из секций длиной 3 м каждая, имеющей в плане треугольное сечение с равными гранями 1 м (рис. 1). Структурные элементы мачты представлены преимущественно трубами диаметром 57 мм и толщиной стенки 5 м, диаметром 32 мм и толщиной 4 мм. Мачта установлена на фундаменте, устойчивость обеспечена шестью оттяжками в два уровня попарно на высоте 9 и 18 м. В качестве оттяжек использован трос диаметром 18 мм.

Для этой конструкции разработаны конечноэлементные модели с использованием одномерных линейных и нелинейных конечных элементов. Линейные элементы предназначены для моделирования поведения стальных структурных элементов мачт в соответствии с теорией напряженного состояния балок С. П. Тимошенко. Использованные нелинейные конечные элементы обладают свойством работать только на растяжение, не воспринимают деформации сжатия и изгиба, предназначены для моделирования оттяжек. Для варьируемых усилий предварительного натяжения оттяжек получены площади A 0 условного стержня, моделирующего оттяжку, и соответствующее значение предварительной деформации (табл. 1). Рассмотрим результаты решения типовых задач.

Таблица 1

Параметры линеаризации мачты высотой 21 м с оттяжками

Усилие H , Н	100	300	500	750	1 000	2 000	3 000	4 000	5 000
σ, МПа	0,8	2,4	4	6	8	16	24	32	40
A 0, мм	0,007	0,198	0,91	3,02	6,93	39,92	76,62	98,70	110
ε, 10–6	4,70	14,1	23,5	35,3	47,0	94,1	141,0	188,0	235,0

Оценка характера деформаций и форм свободных колебаний. Установлено, что основными формами колебаний мачт являются изгибные в двух взаимно перпендикулярных плоскостях (рис. 2) и крутильная (рис. 3). Отклонения от этих форм возникают на высоких частотах колебаний и с позиций проектных расчетов и обеспечения прочности и работоспособности не представляют практического интереса. Частоты первых форм изгибных колебаний равны между собой, частота крутильных колебаний, как правило, меньше, что обусловлено меньшей крутильной жесткостью по сравнению с изгибной.

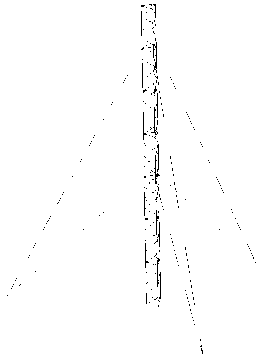
Рис. 1. Модель мачты высотой 21 м:

а – первоначальный конструктивный вариант; б – мачты с двумя поврежденными оттяжками (удалены из модели)

изгибной и крутильной (кривая 1 а ) практически совпадают, вследствие чего кривые их зависимостей на графиках сливаются. Эти значения практически не зависят от усилия предварительного натяжения оттяжек и составляют порядка 10 Гц.

Значения второй изгибной частоты (кривая 1 б ) нелинейно возрастают от 2 до 6,3 Гц по мере увеличения усилия предварительного натяжения оттяжек в диапазоне от 100 до 5 000 Н.

а

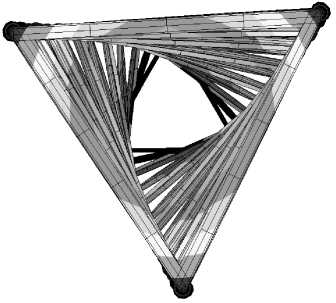
Рис. 3. Крутильная форма свободных колебаний мачты: а – вид сбоку; б – вид сверху (увеличено)

В соответствии с проектными техническими характеристиками рассматриваемая мачта предназначена для размещения на ее вершине технологического оборудования радиотелевизионной и спутниковой связи массой до 530 кг.

б

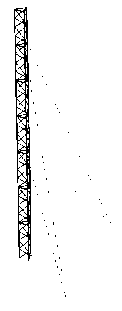
Рис. 2. Изгибная форма свободных колебаний мачты: а – вид сбоку; б – вид сверху (увеличено)

а

Оценка зависимости динамических характеристик мачт от усилия предварительного натяжения оттяжек. На первом этапе выполнен анализ базовых динамических характеристик мачты, не воспринимающей никаких технологических нагрузок.

Варьирование усилий предварительного натяжения позволило установить следующие закономерности (кривые 1 а , 2 а , рис. 4). Значения первых частот –

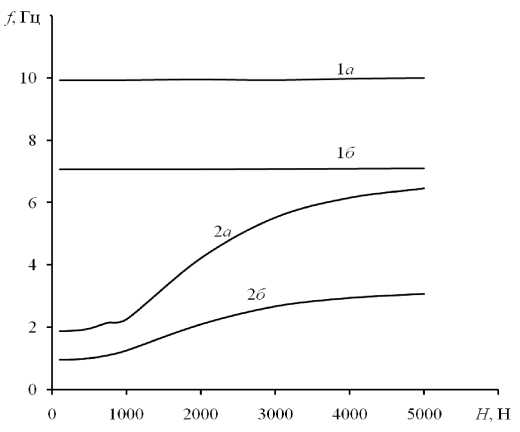
Рис. 4. Зависимости частот собственных колебаний от усилия предварительного натяжения оттяжек: 1 а , 2 а – для мачты, нагруженной собственным весом; 1 б , 2 б – для мачты с размещением на вершине технологического оборудования массой 530 кг

Варьирование усилий предварительного натяжения позволило установить в принципе аналогичные закономерности (рис. 4, кривые 1б, 2б), отличающиеся лишь значениями частот. Значения первых изгиб-ной и крутильной частот (кривая 1б) составляют по- рядка 7 Гц и практически не зависят от усилия предварительного натяжения оттяжек. Значения второй изгибной частоты (кривая 2б) нелинейно возрастают от 1 до 3 Гц по мере увеличения усилия предварительного натяжения оттяжек.

Оценка динамических характеристик мачт с поврежденной оттяжкой. При всем разнообразии возможных сценариев возникновения и развития повреждений и разрушений мачтовых конструкций в эксплуатации [5] в качестве модельной задачи (приняты отличающиеся от ранее решенных задач значения диаметра и предварительного натяжения оттяжек) рассматривается вариант обрыва двух оттяжек в одной вертикальной плоскости (см. рис. 1, б ).

Как видно из полученных результатов (табл. 2), наличие повреждения приводит к снижению первой собственной частоты колебаний, что повышает риски возникновения резонансных явлений, возникновения и развития аварийных ситуаций при действии пульсационной составляющей ветровой нагрузки и сейсмических воздействиях. Аналогичные (качественно) результаты получены для мачты высотой 30 м.

Таблица 2

Частоты собственных колебаний, Гц

№ формы	Частота колебаний мачты (Гц)
	без повреждений оттяжек	с повреждениями оттяжек
1	9,3	5,4
2	9,3	9,3
3	9,9	9,9

Подчеркнем как принципиально важный научный результат: дефекты и повреждения приводят не только к локальному повышению характеристик напряженно-деформированного состояния, но и изменяют динамические характеристики конструкции, вследствие чего возможно резкое изменение ее отклика на динамическое (в данном случае ветровое и сейсмическое) нагружение, что может привести к катастрофическим разрушениям, непропорциональным масштабу первоначального дефекта или повреждения.

Таким образом, постановка и решение таких задач для поврежденных несущих конструкций не только рассматриваемого класса технических систем, но и оборудования в других отраслях открывает потенциальную возможность снижения риска аварий и техногенных катастроф. Это требует постановки и решения задачи экспертизы потенциально опасных объектов с позиций анализа влияния возможных эксплуатационных повреждений на динамические характеристики их несущих конструкций.