Модальный анализ шпиндельного узла на опорах с анизотропными упругими характеристиками

Шпиндельный узел является элементом конструкции металлорежущего станка, непосредственно влияющим на точность и шероховатость изготавливаемых деталей [1]. Среди критериев работоспособности ШУ немаловажным является динамическое качество, опреде-

ляющееся такими характеристиками как собственная частота, демпфирование, амплитуда колебаний с собственной частотой (резонансная амплитуда) [2-4]. Резонансная амплитуда в большей степени зависит от статической жесткости опор шпиндельного узла и ее постоянства в различных направлениях – анизотропии [5-7]. Формы колебаний дают представление об участках шпинделей с наибольшим размахом колебаний, что следует принимать во внимание при проектировании ШУ, в частности при выборе оптимального размещения конструктивных элементов.

В работе [8] представлена математическая модель, показавшая, что анизотропия жесткости опор приводит к появлению диапазона собственных частот. Однако указанная модель не обладает возможностью учета влияния всех конструктивных особенностей исполнения ШУ, а также скорости вращения шпинделя на его динамические характеристики, а именно собственные частоты и формы колебаний.

МЕТОДИКА МОДАЛЬНОГО АНАЛИЗА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК

ШПИНДЕЛЬНОГО УЗЛА МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

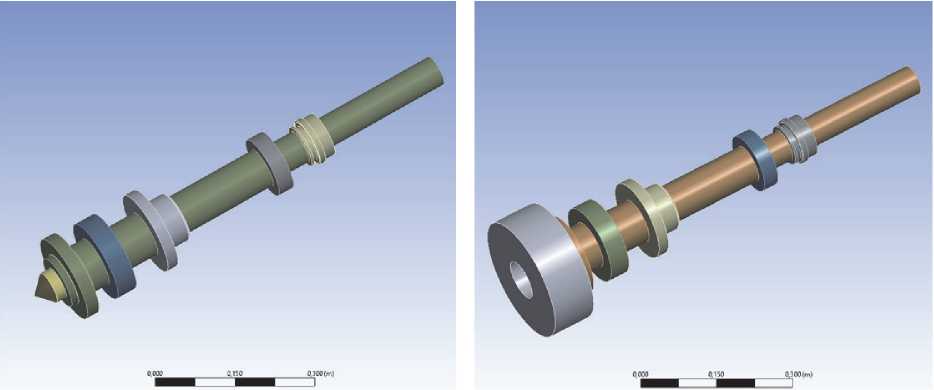
Для оценки влияния различных вариантов исполнений ШУ, анизотропии жесткости опор и частоты вращения шпинделя на собственные частоты и формы колебаний, выполнен модальный анализ динамических характеристик шпиндельного узла токарного станка 16Б16Т1 методом конечных элементов для четырех расчетных моделей (рис. 1). Каждая из указанных моделей включает тело шпинделя и опоры, выполненные в виде сплошных колец, моделирующих упругие характеристики [9] роликового двухрядного конического подшипника с буртом на наружном кольце 4-697713Л (передняя опора) и роликового однорядного конического подшипника с широким наружным кольцом 2-17814Л (задняя опора). Модель I (рис. 1, а) состоит только из тела шпинделя и опор, в модель II (рис. 1, б) добавлены приводная шестерня и полумуфта, модель III (рис. 2, а) помимо указанных выше конструктивных элементов включает неподвижный центр, базирующийся в коническом отверстии переднего конца шпинделя, модель IV (рис. 2, б) вместо неподвижного центра содержит трехкулачковый патрон.

Усредненные значения жесткости опор ШУ получены аналитически по зависимостям работы [10]. В ходе моделирования для учета анизотропии упругих характеристик передней опоры шпиндельного узла расчет проводился для трех вариантов значений жесткостей: усреднен-4с с ное сп, повышенное сп, = — и пониженное Н                          — 1

а)

Рис. 1. Геометрические модели шпиндельного узла токарного станка, не учитывающие наличие технологической оснастки: а – модель I; б – модель II

б)

а)                                      б)

Рис. 2. Геометрические модели шпиндельного узла токарного станка с технологической оснасткой: а – модель III; б – модель IV

с _пг = . Жесткость задней опоры принималась постоянной с усредненным значением с ₃ .

Модули упругости моделей опор найдены с использованием уравнений регрессии, представленных в работе [9]. Для усредненного значения жесткости с _п , физические свойства материала кольца, моделирующего переднюю опору, имеют следующие значения: Е _х = 1,2 - 10 9 Па, E Y = 1,2 - 10 9 Па, E Z = 1,2 - 10 9 Па, G XY = 5 - 10 8 Па,      G_yz = 1,15 - 10 9 Па,      G _XZ = 5,05 - 10 8

Па; для повышенного с _{п t} : E X = 2 - 10 9 Па, E_y = 2 - 10 9 Па, Е₇ = 1,4 - 10 9 Па, О™ = 6 - 10 8 Па, Y                Z                  XY

Gy, = 1,04 -109 Па, Gx7= 5,5 -108 Па; для по-YZ                     XZ ниженного сп2: Ех = 1-109 Па, Ey = 8 -10 Па, Е7 = 7-108Па, Gx== 4,1-108Па, G^ = 7-108 Па' GXZ = 4-108 ПXY

Моделирование осуществлялось с целью определения шести собственных частот и форм колебаний при изменении частоты вращения шпинделя от 0 до 20000 об/мин в зависимости от величины жёсткости передней опоры. Верхняя граница диапазона скорости вращения выбрана на основе расчетов и по рекомендациям Sandvik Coromant [11].

РЕЗУЛЬТАТЫ МОДАЛЬНОГО АНАЛИЗА

В ходе моделирования были найдены значения шести собственных частот и форм колебаний для каждой из расчетных моделей при изменении жесткости передней опоры. Также по результатам расчета построены диаграммы Кэмпбелла, иллюстрирующие зависимость динамических характеристик шпинделя от частоты вращения в указанном диапазоне. Кривые на указанных диаграммах позволяют определить, как величина собственной частоты той или иной формы колебаний меняется в диапазоне скоростей вращения шпинделя. Прямая, проведенная из начала координат, в точках пересечения с кривыми графиков показывает оборотные частоты на которых имеет место явление резонанса [12].

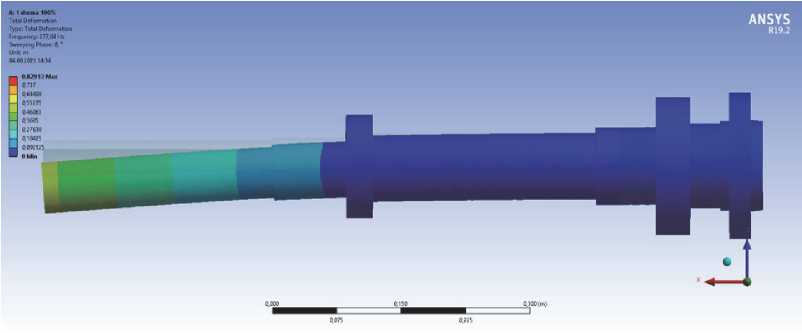
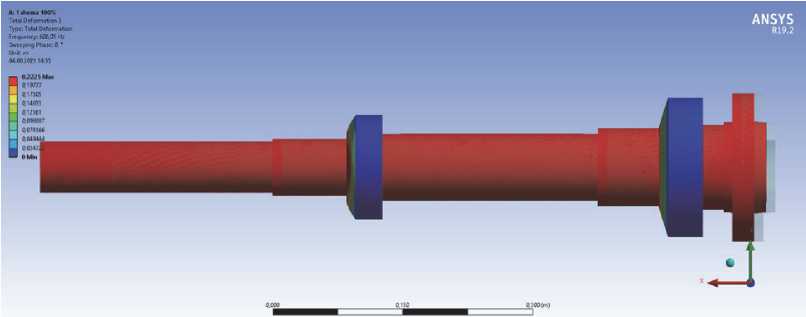
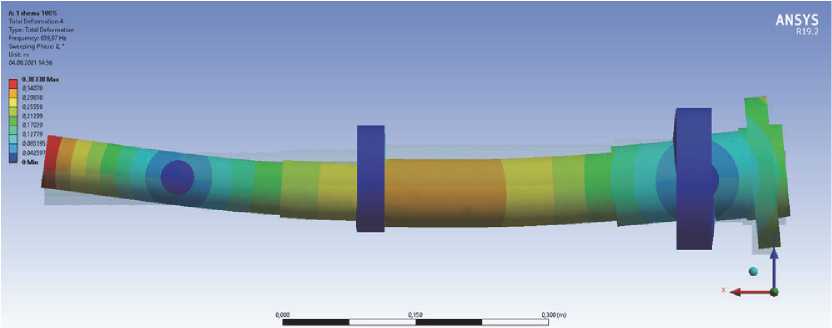
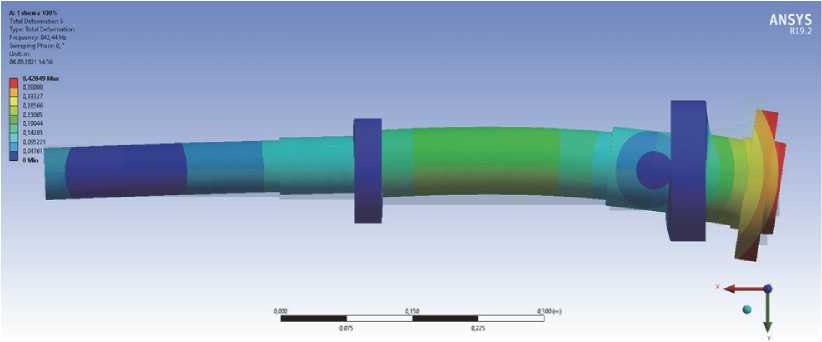
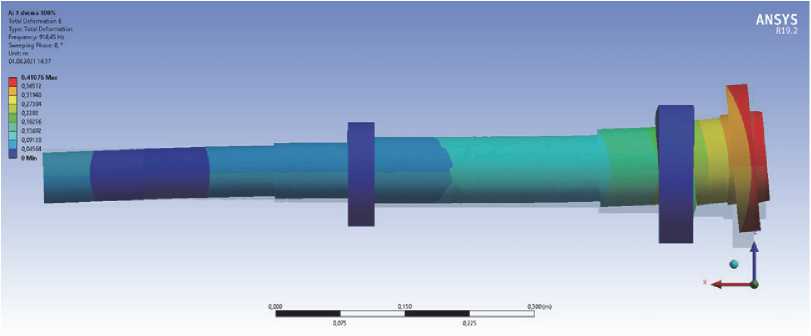
В качестве примера, на рисунках 3 и 4 показаны формы колебаний и диаграмма Кэмпбелла для первой модели ШУ при усредненной жесткости опор.

АНАЛИЗ РЕЗУЛЬТАТОВ МОДАЛЬНОГО АНАЛИЗА

Анализ результатов моделирования показал следующее. Так как модели I и II ШУ не имеют в своем составе технологической оснастки, то колебания на собственной частоте могут возникать только при работе станка на холостом ходу, формы колебаний дают представление об оптимальности конструкции шпиндельного узла в целом. Найденные в ходе расчета первые две формы колебаний характеризуются изгибом консольной части заднего конца шпинделя, третья форма – осевыми колебаниями. Анизотропия жесткости никак не влияет на первые три формы собственных колебаний и на их частоты.

Четвертая, пятая и шестая формы обладают другими закономерностями. В частности, указанные формы колебаний характеризуются изгибом шпинделя с перемещением переднего конца. Повышение жесткости передней опоры приводит к увеличению собственных частот и никак не влияет на формы колебаний шпинделя. При снижении жесткости, помимо уменьшения величины собственных частот происходит изменение вида форм собственных колебаний, которое характеризуется изменением расположения и числа углов поворота тела шпинделя.

Анализ диаграмм Кэмпбелла для моделей I и II показал, что влияние скорости вращения (в рассматриваемом диапазоне от 0 до 20000 об/ мин) на величину собственных частот имеет место лишь для первой модели. При увеличении скорости вращения для любого из значения жесткости передней опоры, отличного от усредненного, снижается пятая (7 Гц) и возрастает шестая (13 Гц) резонансные частоты. Таким образом, анизотропия жесткости совместно с увеличивающейся скоростью вращения оказывает влияние на величины высших собственных частот.

Модели III и IV имеют в своей конструкции элементы технологической оснастки и исследование собственных частот и форм колебания на примере данных моделей можно использовать для оценки влияние резонансных вибраций на точность обработки.

Третья модель имеет формы колебаний схожие с ранее рассмотренными моделями (I и II) и аналогичные закономерности влияния анизотропии жесткости на формы и частоты собственных колебаний. С точки зрения влияния технологической оснастки на формы колебаний можно сказать, что установка центра оказывает определенное воздействие на изгиб шпинделя при резонансных частотах за счет увеличения массы шпинделя и смещения центра тяжести ближе к передней опоре: происходит изменение положения узлов конечно-элементной модели, относительно которых происходит изгиб тела шпинделя на четвертой, пятой и шестой собственных частотах. Диаграммы Кэмпбелла подтверждают, что для третьей модели ШУ скорость вращения в рассматриваемом диапазоне от 0 до 20000 об/мин, а также изменение жесткости передней опоры никак не влияют на величину собственных частот.

ANSYS

a)

в)

r)

д)

e)

Рис. 3. Формы собственных колебаний ШУ модели I при усредненной жесткости опор: а – первая форма; б – вторая форма; в- третья форма; г – четвертая форма; д – пятая форма; е – шестая форма

Frequency (Hz)

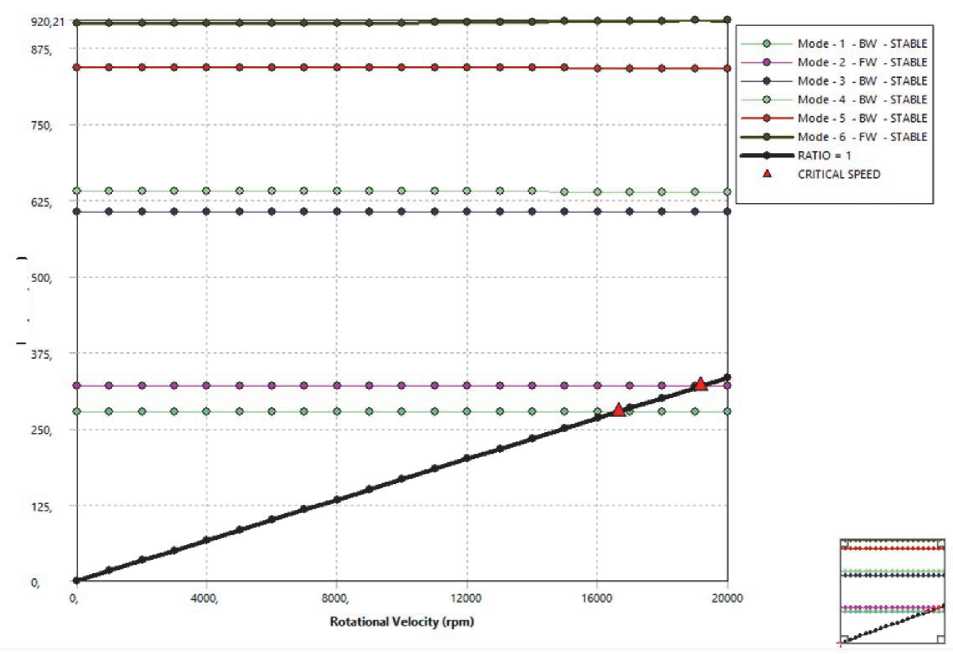
Рис. 4. Диаграмма Кэмпбелла для I модели при усредненной жесткости опор

Для четвертой модели ШУ характерны существенные отличия форм колебаний. Первая и вторая формы – это изгибные колебания, характеризующиеся деформацией шпинделя и перемещением переднего конца. Третья собственная форма колебаний аналогична первой форме колебаний для первой, второй и третьей моделей.

Четвертая форма колебаний – крутильная. Пятая форма колебаний совпадает со второй формой, характерной для ранее рассмотренных моделей. Шестая форма – осевые колебания. Таким образом, наличие патрона приводит к появлению новых форм колебаний, что не может не влиять на точностные характеристики станка.

Таблица 1. Собственные частоты различных конструктивных исполнений шпинделя, Гц

Номер собственной частоты	Жесткость передней опоры	I модель	II модель	III модель	IV модель
Первая	Усредненная	277,64	299,36	299,57	254,87
	Повышенная	277,68	299,54	299,78	258,87
	Пониженная	276,82	297,9	297,88	225,87
Диапазон частот		0,86	1,64	1,9	33
Вторая	Усредненная	319,34	363,02	362,79	261,32
	Повышенная	319,8	363,75	363,55	280,6
	Пониженная	318,17	362,33	362,04	246,05
Диапазон частот		1,63	1,42	1,51	34,55
Третья	Усредненная	606,01	609,93	564,15	301,01
	Повышенная	628,56	620,49	574,02	301,02
	Пониженная	568,97	552,48	510,51	300,8
Диапазон частот		59,59	68,01	63,51	0,22
Четвертая	Усредненная	639,97	697,63	678,8	322,39
	Повышенная	642,37	701,92	691,92	340,21
	Пониженная	632,7	623,6	548,92	305,36
Диапазон частот		9,67	78,32	143	34,85
Пятая	Усредненная	842,44	791,58	682,64	363,65
	Повышенная	862,09	835,12	712,23	366,11
	Пониженная	731,53	713,68	611,39	362,29
Диапазон частот		130,56	121,44	100,84	3,82
Шестая	Усредненная	914,45	807,82	693,11	418,32
	Повышенная	922,15	926,21	793,66	425,64
	Пониженная	748,56	716,35	680,42	378,67
Диапазон частот		173,59	209,86	113,24	46,97

Анализ диаграммы Кэмпбелла показал, что для четвертой модели характерно достаточно существенное влияние скорости вращения на величины частот второй, четвертой и пятой форм колебаний. При усредненной жесткости передней опоры вторая собственная частота снижается на 40 Гц, четвертая возрастает на 38 Гц, пятая возрастает на 22 Гц; пониженная жесткость: вторая собственная частота снижается на 48 Гц, четвертая возрастает на 55 Гц, пятая возрастает на 21 Гц; повышенная жесткость: вторая собственная частота снижается на 30 Гц, четвертая возрастает на 19 Гц, пятая возрастает на 22 Гц. Таким образом по сравнению с другими моделями шпиндельного узла наличие патрона привело к появлению нелинейных зависимостей между скоростью вращения шпинделя и величинами собственных частот. Анизотропия жёсткости передней опоры также существенно влияет на указанную взаимосвязь, приводя к появлению диапазона изменения величины собственной частоты при изменении оборотов шпинделя.

В таблице 1 представлены значения собственных частот для моделей шпиндельного узла с учетом анизотропии жесткости передней опоры. Анализируя таблицу, можно сделать вывод, что для первых трех моделей ШУ изменение жесткости передней опоры не влияет на величины первой и второй собственных частот, во всех остальных случаях имеет место диапазон собственных частот, вызванный анизотропией жесткости передней опоры.

ЗАКЛЮЧЕНИЕ

Таким образом, на основании проведенных исследований установлено, что конструктивные факторы оказывают существенное влияние на формы колебаний и собственные частоты шпиндельного узла. Из рассмотренных расчетных моделей предпочтение следует отдать моделям, учитывающим технологическую оснастку. В этих моделях наблюдается появление новых форм колебаний, что влияет на точностные характеристики станка. Сравнение динамических характеристик ШУ при возможной обработке в центрах и при использовании патрона показало, что при обработке в центрах на точность будет влиять четвертая собственная частота и форма колебаний, при использовании патрона – первая. Принимая во внимание, что разница между ними более чем в 2,5 раза, то обработка в центрах может вестись при существенно больших скоростях резания.

Изменение жесткости передней опоры в рамках принятого диапазона не влияет на формы колебаний в тех случаях, когда возникают вибрации консольной части заднего конца шпинделя или осевые колебания. Анизотроп- ные упругие свойства опор приводят к возникновению диапазона собственных частот для каждой формы колебаний, который может составлять до 200 Гц. К появлению диапазона собственных частот приводит также непостоянство упругих характеристик опор шпинделя. Причем, в пределах указанного диапазона собственные частоты изменяются в зависимости от скорости вращения шпинделя.