Модальный анализ тактильного механолюминесцентного оптоволоконного покрытия при вдавливании жестких шаровых частиц

Цитирование: Паньков А. А. Модальный анализ тактильного механолюминесцентного оптоволоконного покрытия при вдавливании жестких шаровых частиц / А. А. Паньков, П. В. Писарев, С. Р. Баяндин // Журн. Сиб. федер. ун-та. Техника и технологии, 2024, 17(5). С. 578–588. EDN: MLENOX в гибких тактильных покрытиях пьезоэлектрических полимерных поливинилденфторид-ных пленок PVDF [16–18] с уникальными физико-механическими свойствами. Идеальный тактильный датчик имеет высокую чувствительность (отношение изменения выходного сигнала к изменению диагностируемого параметра), быстрый отклик, надежность и стабильность характеристик. Фундаментальные характеристики тактильных датчиков в первую очередь определяются их активным слоем, который является наиболее важным компонентом тактильных датчиков, так как именно активный слой непосредственно воспринимает диагностируемые физические и/или механические величины из внешней среды: давление, температуру и деформацию, и преобразовывает их в различные оптические или электрические сигналы: ток, напряжение, сопротивление и емкость. Например, пьезоэлектрический активный слой [14–18] функционирует через преобразование механической энергии в электрическую, и в результате при внешнем силовом воздействии пьезоэлектрический слой генерирует электрический заряд, который прямо пропорционален величине измеряемой силы. Пьезоэлектрические элементы в составе оптоволоконного датчика, встроенного в полимерный слой, позволяют диагностировать, например, обледенение слоя и осуществлять автоматическую резонансную самоочистку поверхности слоя от корки льда [22], изучать внешний объект при контактном взаимодействии ворсинок (вибрисс) полимерного слоя с поверхностью анализируемого объекта [23].

Цель – выявление и анализ закономерностей влияния на резонансные характеристики вынужденных электромеханических колебаний представительного фрагмента (ячейки) тактильного покрытия диагностируемой величины силы P вдавливания в его сенсорную поверхность множества однотипных жестких шаровых частиц.

Вычислительная электромеханическая модель тактильного покрытия

Рассматриваемое тактильное покрытие – полимерный слой со встроенным (например, в виде спирали Архимеда) оптоволоконным пьезоэлектролюминесцентным (PEL) датчиком (рис. 1) [20] в виде световода с покрытиями из электролюминесцентного и пьезоэлектрического слоев. Электролюминесцентный и пьезоэлектрический слои структурированы в виде

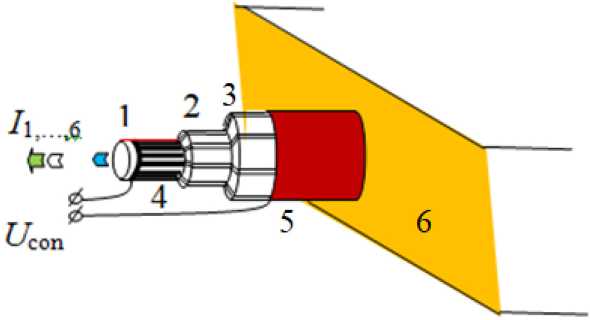
Рис. 1. Оптоволоконный PEL-датчик объемного деформированного состояния, где 1 – световод, 2, 3 – электролюминофор и пьезоэлектрик, 4, 5 – управляющие электроды, 6 –полимер

Fig. 1. Fiber optic PEL-sensor of volumetric deformed state, where 1 is a light guide, 2, 3 are EL phosphor and piezoelectric, 4, 5 are control electrodes, 6 is a polymer

a b

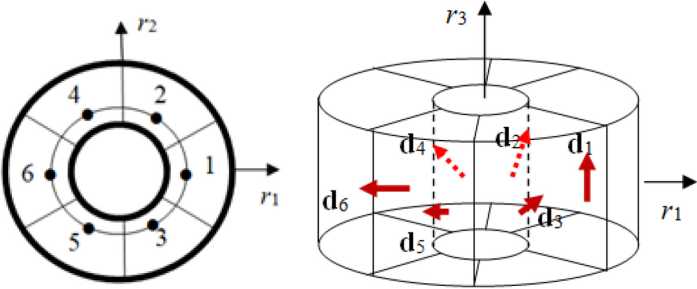
Рис. 2. Взаимное расположение пьезоэлектрических секторов (а) с различными направлениями d _k пространственных поляризаций (b); (•) -точки измерения электрических потенциалов

Fig. 2. Mutual location of piezoelectric sectors (a) with different directions dk of spatial polarizations (b); (•) – electrical potential measurement points шести пар круговых составных (двухфазных) секторов «электролюминофор/пьезоэлектрик», протяженных вдоль цилиндрической поверхности световода (рис. 2). Первый светопрозрачный и второй электроды (в виде цилиндрических электродированных поверхностей) расположены на межфазной поверхности «световод/ электролюминесцентный слой» и на внешней поверхности пьезоэлектрического слоя соответственно. Электроды являются общими для всех составных секторов «электролюминофор/пьезоэлектрик» и образуют непрерывную (вдоль оси датчика) двухпроводную линию с выходами для подключения к ним управляющего электрического напряжения Ucon.

При приложении к выходам электродов переменного электрического напряжения U _con возникают электромеханические колебания (вибрации) PEL-датчика с проявлением «механолю-минесцентного эффекта» – результата электрического взаимодействия пьезоэлектрического и сопряженного с ним электролюминесцентного секторов внутри каждой k -й пары «электро-люминофор/пьезоэлектрик» датчика при его деформировании в составе тактильного покрытия, k =1,…,6. В результате механолюминесцентного эффекта в электролюминесцентном секторе каждой k -й пары «электролюминофор/пьезоэлектрик» генерируются в своем частотном диапазоне f_k . информативные световые импульсы; результирующие значения интенсивностей I_k для каждой частоты f_k измеряются на выходе из световода.

Считаем, что пьезоэлектрические секторы (рис. 2b) различаются между собой лишь ориентациями направления поляризации – оси симметрии трансверсально-изотропных электро-упругих свойств полимерного пьезоэлектрика PVDF, d _k – единичные направляющие вектора для различных секторов с координатами

d ( k )1 =cosϕ k sinθ k , d ( k )2 =sinϕ k sinθ k , d ( k )3 =cosθ k , (1)

где ϕ, θ – углы сферической системы координат: ϕ _k= π( k -1)/3, θ₁=0, θ₂=π/3, θ₃= –π/3, θ₄=2π/3, θ₅= –2π/3, θ₆=π, координатная ось z = r ₃. Компоненты трансверсально-изотропных тензоров упругих свойств C _k , пьезомеханических коэффициентов e _k , диэлектрических проницаемостей λ _k для k -го пьезоэлемента датчика с единичным направляющим вектором d _k (1) поляризации в координатных осях r_i представим разложениями [25]: 1) для упругих свойств в виде

^ ” ^ c(p)T(p)

P=1

через компоненты базисных тензоров

T^inkl — ^in^kl> T^inkl ^in^kdir ^(s^mkl — ^kl^idn/

^(4)inkl didndkdi,T^}inkl — aikOnl + ^il^nk>

^^inki ^ik^ndi “Ь aiid-ndk 4- ct^d^di + cinididk, и пять независимых констант упругости: C(l) — C12< C(2) — C(3) — C13< C(4) — C33< C(5) — C66’ C(6) — C55< выполняются равенства

Qi ^(i) + 2C(5), dij S[j didj, символ Кронекера δ;

• 2)    для пьезомеханических свойств

eimn ^3i^i^mn "•" (^зз ^3i 2ei^didmdn+ei5(dm6in + dnd[m), где e33, e31, e15 – независимые константы;

• 3)    для диэлектрических свойств

^■in ^-l^in + (^3 h^)djdn c использованием независимых компонент: c12, c13, c33, c66, c55, e33, e31, e15, λ1, λ3 трансверсальноизотропных тензоров упругих C, пьезоэлектрических e и диэлектрических λ свойств в главных осях ξi в матричной форме записи пьезоэлемента PVDF с поляризацией по оси ξ3 соответственно.

При электромеханическом нагружении и, как следствие, вибрациях PEL-датчика в составе тактильного покрытия имеем результирующие величины электрических напряжений

U ( k )lum = a con( k ) U con + b ( k ) ij ε ij                                                                  (2)

на электролюминесцентном элементе k -го сектора датчика, где управляющие a _con ( _k ) и информационные b ( k ) передаточные коэффициенты датчика могут быть найдены экспериментально или с использованием современных численных методов. Формула (2) представляет величину электрического напряжения U ( k )lum в виде линейного разложения по значениям компонент ε ij тензора «макродеформации» ε (обусловленной вынужденными колебаниями тактильного покрытия и действием внешнего силового воздействия, т.е. вдавливания жестких частиц) датчика и управляющим электрическим напряжением U _con, приложенным к выходам электродов датчика.

Модальный анализ тактильного покрытия

Модальный анализ – нахождение собственных форм и резонансных частот колебаний тактильного покрытия при действии на него внешних силовых воздействий осуществлен в результате численного конечно-элементного решения стационарной задачи электроупругости в пакете ANSYS для составной ячейки периодичности с одиночной шаровой частицей – 582 –

(рис. 3) в Центре высокопроизводительных вычислительных систем ПНИПУ. Расчетная область – прямоугольный параллелепипед «полимерный слой/встроенный датчик/шаровая частица» (рис. 3) с условиями симметрии для электроупругих полей на его боковых гранях, основание – нижняя грань ячейки периодичности считалась неподвижной.

Геометрические параметры расчетной области (ячейки периодичности на рис. 3) были заданы через размеры ячейки периодичности: l = 30 мм, b =12 мм, h = 3.5 мм – длина, ширина и толщина параллелепипеда в виде слоя с ребрами по координатным осям r_i . При этом ось r ₃ проходит по центру составной ячейки (слоя) и является продольной осью встроенного в слой оптоволоконного PEL-датчика при значении радиусов световода r ( ₁ ) =1мм и радиусов r ( ₂ ) =1.2мм, r ( ₃ ) =1.4мм межфазных границ «световод/электролюминофор» и «электролюминофор/пьезо-электрик» соответственно. При численном моделировании область ячейки периодичности (рис. 3) разбивалась на 18‧10⁶ конечных элементов, включая 12‧10⁶ для области PEL-датчика, шаровая частица абсолютно жесткая. При численном решении системы линейных алгебраических уравнений использован итерационный решатель метода сопряженных градиентов, что позволило значительно сократить (с 18 до 7,5 часов) время счета в сравнении с использованием прямого решателя SPARSE.

В результате модального анализа представительной области в виде ячейки периодичности (рис. 3) найдены первые шесть собственных форм (рис. 4) и резонансных частот ν_rez ( _n ) (рис. 5) колебаний тактильного покрытия для рассматриваемого случая (рис. 3) вдавливания множества жестких шаровых частиц. Установлены закономерности влияния значений силы P вдавливания на каждую из резонансных частот ν_rez ( _n ) колебаний (рис. 5) ячейки периодичности (рис. 3) индикаторного полимерного PEL-покрытия, здесь n =1,…,6. Выявлено (рис. 5), что при значениях силы P более 0.01Н значение коэффициента k _ν =Δν_rez ( _n ) /Δ P ≈ –1236 Гц/Н практически постоянно для всех шести первых собственных частот ν rez( n ) в виде линейного представления

ν rez( n ) = ν 0( n ) + k ν P . (3)

Установленные зависимости (рис. 5) резонансных частот ν rez( n ) ячейки периодичности (рис. 3) и их линейные аппроксимации (3) позволяют использовать алгоритм резонансного

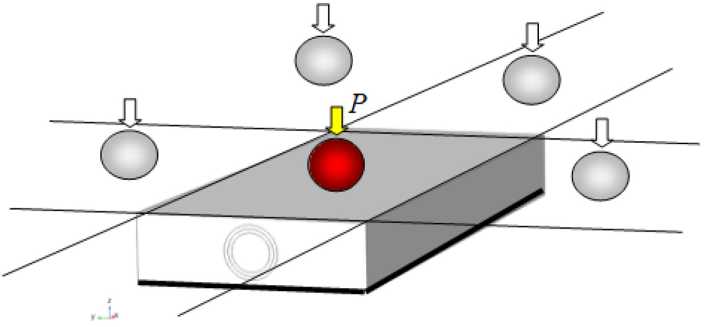
Рис. 3. Ячейка периодичности многоточечного силового воздействия

Fig. 3. Multipoint force frequency cell

e                                                        f

Рис. 4. Собственные формы колебаний ячейки вдавливания P =0.1 Н жесткой шаровой частицы

периодичности тактильного покрытия при силе

Fig. 4. Natural vibrations of tactile coating periodicity cell at indentation force P = 0.1 N of rigid ball particle

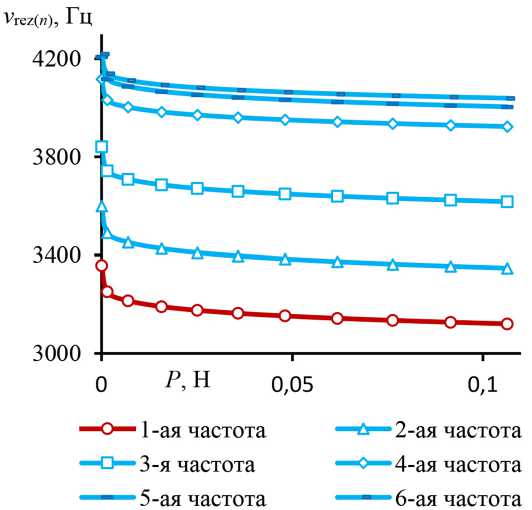
Рис. 5. Влияние силы P вдавливания частиц на собственные частоты ν_rez ( _n ) колебаний тактильного покрытия

• Fig. 5.    Influence of particle indentation force P on natural frequencies ν_rez ( _n ) of tactile coating oscillations

t/lum(fc), В                                      Mum®, В

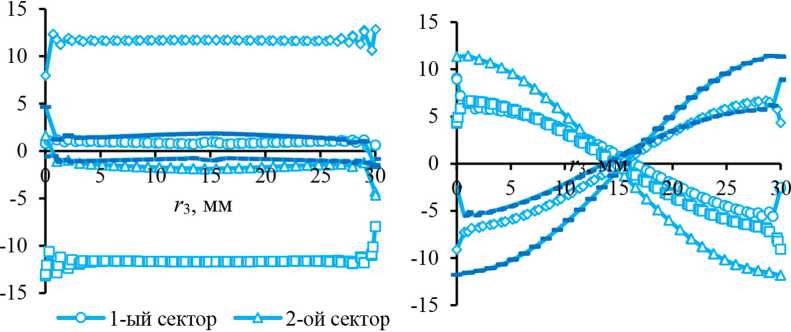
—о—3-ий сектор —о—4-ый сектор        1-ый сектор 2-ой сектор

_ „          —о—З-ий сектор   —5—4-ый сектор

— 5-ыи сектор —6-ои сектор                       „

5-ыи сектор б-ои сектор a                                              b

Рис. 6. Распределения электрических напряжений U lum( k ) вдоль k -го сектора электролюминофора для первой (а) и второй (b) форм колебаний покрытия при силе вдавливания P =0.1 Н частиц

• Fig. 6.    Distribution of voltages U lum( k ) along the k -th sector of the electrophosphor for the first (a) and second (b) forms of coating vibrations at the indentation force P = 0.1 N of particles

диагностирования [21] и находить величину внешнего силового воздействия P по измеренным информативным изменениям резонансной частоты колебаний индикаторного полимерного PEL-покрытия. На практике по форме оптических сигналов, обусловленной зависимостью величин электрических напряжений U ( k )lum на слоях секторов электролюминофора, можно сделать вывод о номере n реализованной резонансной частоты. На рис. 6 изображены графики распределений электрических напряжений U _lum ( _k ) вдоль секторов электролюминофора («измеренных» в контрольных k -х точках секторов на рис. 2а) для первой (рис. 5, рис. 6а) и второй (рис. 5, рис. 6b) форм колебаний представительного фрагмента (рис. 3) покрытия при силе вдавливания P =0.1 Н частиц. Характер распределений величин U _lum ( _k ) по продольной координате r₃ секторов электролюминофоров датчика обуславливает форму k -х световых импульсов на выходе из световода, что дает возможность идентификации реализующейся на практике резонансной формы колебаний.

Выводы

Представлена вычислительная электромеханическая модель тактильного механолю-минесцентного оптоволоконного покрытия (рис. 1) резонансного метода диагностирования внешних силовых воздействий для случая вдавливания в его внешнюю сенсорную поверхность множества однотипных и периодическим образом распределенных по поверхности жестких шаровых частиц (рис. 3). Сенсорные характеристики тактильного покрытия обуславливаются встроенным в него оптоволоконным пьезоэлектролюминесцентным датчиком (рис. 1, рис. 2), в котором механолюминесцентный эффект – это результат электрического взаимодействия деформируемого пьезоэлектрического слоя на смежный с ним электролюминесцентный слой датчика. В режиме диагностирования при контактном взаимодействии – 585 – сенсорной поверхности покрытия с жесткими шаровыми частицами вынужденные электромеханические колебания (рис. 4) тактильного покрытия (рис. 3) инициируются переменным управляющим электрическим напряжением Ucon, приложенным к выходам электродов датчика (рис. 1). Необходимые для резонансного метода динамические характеристики: собственные формы и зависимости резонансных частот тактильного покрытия от величины диагностируемого параметра – силы P вдавливания частиц (рис. 3) определены на основе численного конечно-элементного решения стационарной задачи электроупругости в пакете ANSYS для составной ячейки периодичности с одиночной шаровой частицей (рис. 3). Расчетная область – прямоугольный параллелепипед «полимерный слой/встроенный датчик/ шаровая частица» (рис. 3) с условиями симметрии для электроупругих полей на его боковых гранях, нижняя грань (основание) ячейки периодичности неподвижна. В результате модального анализа ячейки периодичности найдены собственные формы и резонансные частоты νrez(n) колебаний тактильного покрытия для рассматриваемого случая (рис. 3) вдавливания множества жестких шаровых частиц. Исследованы (рис. 5) закономерности влияния величины силы P вдавливания частиц на резонансные частоты νrez(n) первых шести форм колебаний (рис. 4) тактильного покрытия. Выявлен (рис. 5) близкий к линейному характер, и найдено численное значение коэффициента kν пропорциональности (3) зависимостей резонансных частот νrez(n) тактильного покрытия от величины силы P вдавливания частиц при значениях силы более 0.01Н, что эффективно при использовании резонансного метода для диагностирования рассматриваемых силовых воздействий.