Модальный конечно-элементный анализ балок, податливых при трансверсальном сдвиге

Композиционные материалы часто используются в производстве ракетно-космической техники, поскольку они, обладая высокими удельными механическими свойствами, позволяют изготавливать конструкции с большой степенью весового совершенства. Для композитов характерна низкая трансверсальная сдвиговая жесткость. Эту особенность поведения композитов необходимо учитывать при проектировании и расчете. Математическая модель при этом усложнится по сравнению с той, что используется при расчете конструкций из традиционных материалов.

Рассматривается задача о собственных колебаниях балок, податливых при трансверсальном сдвиге. Решение выполняется с помощью метода конечных элементов (МКЭ). Математическая модель базируется на теории пластин Рейсснера-Мидлина [1; 2]. Для вывода матриц жесткости и инерции используется вариационный подход. Для этого выражение полной энергии конечного элемента колеблющейся балки варьируется по узловым компонентам, среди которых присутствуют осредненные по высоте сечения углы трансверсального сдвига. Разработанная конечноэлементная модель протестирована на примерах решения классических задач. Ее актуальность показана расчетами, выполненными для монолитных изотропных балок с низкой трансверсальной сдвиговой жесткостью, для трехслойных балок с податливым заполнителем, а также для балок, изготовленных из однонаправленного композита (ортотропная модель). Частоты и формы собственных колебаний подтверждаются конечно-элементными решениями в среде пакета COSMOS/M, где эти задачи рассматривались в более строгой (двумерной) постановке.

Исследуемая конечно-элементная модель допускает описание граничных условий неклассического вида, когда на торцах балки регламентируется поведение углов трансверсального сдвига. Показано, что для некоторых типов граничных условий задача о собственных колебаниях балки не может быть решена при использовании классических расчетных моделей.

Получим разрешающие уравнения для задачи о свободных поперечных колебаниях балки с низкой трансверсальной сдвиговой жесткостью. Задачу будем решать с помощью МКЭ, поэтому сначала необходимо записать выражение энергетического функционала. Полная энергия колеблющейся балки скла-

дывается из потенциальной энергии деформации и кинетической энергии движения:

AW       AW

E = U + T .

Здесь

U = ¹ J J J ( 6 x e x + ⁶ z e z + ^T xz e xz ) dxdydz ,

2 ( V )

T = ~J j Jp( x,У,z ) ^v 2 dxdydz ,

² ( V )

где ρ – плотность материала в точке с координатами ( x, y, z ); v – скорость движения этой точки тела; V – объем тела.

Последовательно применяя гипотезы о поведении балки с низкой трансверсальной сдвиговой жесткостью [3], вместо (1) получим

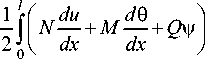
1 i I

Л J ] b p ( u 2

² о I

x dx = 0,

dx —

+ w ²) + 2 Cu I V- dw ^| + D_o ' ^p Г dx ^{J p}

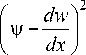
^X

где N , M , Q – внутренние балочные усилия ( N – продольная сила, М – изгибающий момент, Q – перерезывающая сила), вычисляемые по формулам

„du i\ d V d 2 w I N = B — + C — _T , dx I dx   dx² I

„du    I dw d^w I

M = C"T + D\- T —Г , Q = K V , dx     I dx dx² J

где B _ρ, С _ρ, D _ρ – параметры, характеризующие инерционные свойства

bb

2 h—^2

Bp = J J pdydz, Cp = J J pzdydz, b — sb b 2 h — s

Dp = J J p z2 dydz.(5)

b — s 2

Здесь h и b – высота и ширина сечения балки соответственно.

Перейдем теперь непосредственно к формированию матрицы жесткости балочного конечного элемента. Будем полагать, что прогиб изменяется по кубическому закону вдоль длины элемента, а угол сдвига ψ и продольное перемещение u – по линейному закону:

w ( x ) — a 1 + a₂ x + a₃ x ² + a₄ x ³ , v ( x ) — a₅ + a₆ x ,

u ( x ) —a₇ +a₈ x .                (6)

Введем в рассмотрение вектор основных кинема-

тических переменных

,   | dw о = 1 w — v u

I dx

Вектор узловых кинематических параметров произвольного элемента балки представим в следующем виде:

Т s I       I dw I                        I dw II oe = s w1  I — I   v1  u1  w2  I — I   V2  u2 r

I    I dx J1                I dxA

s 23	D p 1 12 ,	Cl	13 B l 2 D
		p	p         p
		' 24        12 ,      ' 25	420    10
s 26	— - ~ B 140 p	Dl 1 3-- D01 , ' 27 — — 30 p         27     12	C p 1 ,     '? — ,      28      12
s 33	d p 1 3 ,	C p 1            D p ' 34 — — , ' 35 — - "J" ,	— D p 1 36      2
s 37	D p 1 6 ,	C p 1           B p 1 ' 38 —        ,     ' 44 —        , 63	C p ' 45 — - T
s 46	— C D 1  ' 12 , 47	_ c p 1      _B p 1      _ — 4 , ' 48 — 4 , ' 55 — 66	13 B p 1 2 + 42 D p
			35 l
s 56	— - 11 b p 1 2 210	- D p     ' —- D p 10 ,         57        2 ,	5 =-c p ' 58       2
s 66	— ~ B 13 105 p	2 _ ,            D p 1 + D p 1 , ' б7 —, 15 p        67       12	— - C p 1 68       12
s 77	— D p 1      — C p 1      — B p 1 3 , s 78       3 , s 88       3 .

Следуя вариационному подходу к МКЭ, получим систему уравнений для произвольного балочного элемента, которая в матричном представлении имеет следующий вид:

K e δ e – ω ² S e δ e = 0 ,

где K e и S e – матрица жесткости и матрица инерциальных параметров балочного элемента балочного

элемента со тами:

следующими ненулевыми

компонен-

С помощью матриц K e и S e формируются глобальные матрицы жесткости и инерции K Σ и S Σ , фигурирующие в глобальных уравнениях состояния

KΣ Δ – ω2 SΣ Δ = 0,(10)

где глобальный вектор узловых неизвестных имеет вид

Δ = {δ1 δ2 … δi … δn+1}Т,(11)

δ _i – вектор узловых неизвестных i -го узла

Т

= _ I      I dw 1I

°i = 1 w         I v i u i \ .

I       V dx J iI

D k11   12

l

3 ,

k 12

k 22

= 4 D

k 23

D

= 6-r, l ²

D

= -7 ’

k 15 =- 12 D

C

D k16 = 612,

k 24

l

D k25 = 6

l

2 ,

k 26

k ₃₆

k ₄₆

= 2 D l

D

= 7 ’

C

= 1 ’

, k

DC

' 27 = 1 ’ k 28 = 1 ’ ^k 33

DKl

=     + ,, , ^k 34

l

k 56

k 77

s 11

s 14

^k 37 =

k ₄₇

DKl 7⁺"6",

C

= 1 ’

k 38 =

k 48 =

C l ^,

k

C l ^, B

'⁴⁴      1 ’

=- 6 A

DKl

—1-- l3

k 66 = 4 D ’

k 67 =

B l ^,

D

- 7 ’

k 55 = 12 D

k 68 =

C l ^,

CB

, ^k 78 = 1 ’ ^k 88 = 1 ’

13 B _p 1 ² + 42 D _p

35 l

11 B p 1 ²

, ' 1₂ ——"—

12     210

+ D p , 10

s 13

D

,

C P 5 -2 , ' 1⁵ =

3 ( 3 B _p 1 ² - 28 D _p )

70 l

_ - 13 B p 1 ²

, s 16        420

+ D p , 10

Описанный алгоритм вывода матрицы жесткости и матрицы инерции реализован в специальной программе формирования фундаментальных матриц и векторов теории МКЭ, предназначенных для расчета балок, податливых при трансверсальном сдвиге [4].

Выполним тестовое решение для стальной ( Е = 210 ГПа, μ = 0,3, ρ = 7 800 кг/м ³ ) балки длиной 1 м, с прямоугольным поперечным сечением ( h = 1 см, b = 1 мм). Будем полагать, что координатная ось X проходит через центры тяжести сечений. В этом случае смешанные жесткости ( С ), фигурирующие в матрице жесткости элемента K _e ,и параметр инерции ( С _ρ ), присутствующий в матрице S _e , равны нулю.

Сначала в нашем КЭ расчете зададим граничные условия свободного опирания, причем углы сдвига ψ на торцах не фиксируются:

при x = 0: w = 0, u = 0, при x = L : w = 0.    (12)

Результат сравним с классическим решением, определяемым по формуле

i 2n2 7 J ^ю - = rr A — , L ²    m

- D p     -D p

' 17 —     , ' 17 —

17     2      17     2

C

, ' 18 = — , ' ₂₂ =-- BJ ³ + — Dl ,

, ¹⁸     2 , ²² 105 ^p 15 ^p

где J – момент инерции сечения.

С помощью программы [5] решена обобщенная задача на собственные значения для 50-узловой моде- ли стальной балки длиной 1 м с прямоугольным поперечным сечением (h = 1 см, b = 1 мм) и получено значение первой круговой частоты, равное 147,811 (рад/с). Вычисленное по формуле (13) значение равно 147,833 (рад/с). Форма колебаний при этой частоте показана на рисунке.

Представлены первые пять частот собственных колебаний стальной балки, определенные по нашей модели, вычисленные по формуле (13) и найденные в результате решения в пакете COSMOS/M с использованием элементов PLANE2D (табл. 1). Почти идеальное совпадение по частотам подтверждает правильность рассматриваемого здесь подхода. Совпадение имеет место и по формам колебаний. Отметим, что результаты модального анализа в пакете COSMOS/M выдаются в виде циклической частоты f , измеряемой в Гц (с ^–1 ) и связанной с круговой частотой формулой ω = 2 π f .

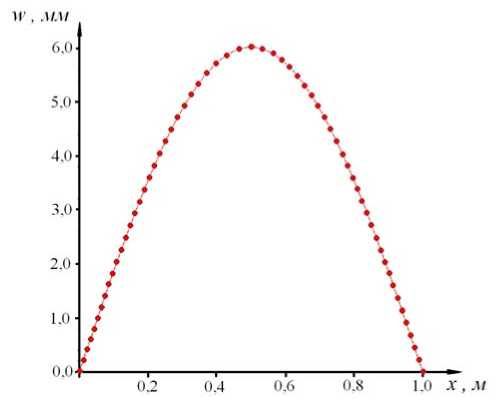
Первая форма колебаний балки

Таблица 1

Частоты собственных колебаний для первых пяти мод

Номер моды	Тестируемое решение	Аналитическое решение	Решение в пакете COSMOS/M
1	147,811	147,833	147,809
2	590,982	591,332	590,956
3	1 328,730	1 330,497	1 328,605
4	2 359,758	2 365,328	2 359,361
5	3 682,269	3 695,826	3 681,293

Важно отметить, что в данном случае частоты первых мод колебаний являются первыми в списке собственных значений задачи, т. е. наименьшими.

Выполним модальный анализ, уменьшив в 100 раз (по сравнению с предыдущим расчетом) жесткость балки при трансверсальном сдвиге. Все остальные параметры жесткости, размеры и граничные условия оставим без изменения. Результаты решения по нашей модели представлены списком первых пяти собственных значений задачи, расположенных во втором столбце (табл. 2). Здесь же для сравнения приводится решение (табл. 2, третий столбец), выполненное в пакете COSMOS/M, в котором для учета уменьшенного параметра трансверсальной жесткости задействуется опция ортотропных свойств материала (для элементов PLANE2D). При этом фактически уменьшается соответствующий модуль сдвига в списке механических свойств материала. Вновь отмечаем хорошее совпадение результатов. Подчеркнем необходимость учета трансверсального сдвига в модальном анализе. Сравнение соответствующих данных (см. табл. 1 и 2) показывает заметное расхождение частот собственных колебаний, определенных с учетом трансверсального сдвига, и теми же величинами, вычисленными по классической формуле, где этот эффект не принимается во внимание.

Выполнено решение задачи о собственных колебаниях балки с шарнирно-опертыми концами, на которых зафиксирован угол трансверсального сдвига. В этом случае рассматривается разрешающая система алгебраических уравнений со следующими граничными условиями:

при x = 0: w = 0, u = 0, ψ = 0, при x = L: w = 0, ψ = 0. (14)

Результаты решения (первые пять частот) приведены в четвертом столбце (табл. 2). Они показывают, что для рассматриваемой здесь шарнирно-опертой балки (с данным набором геометрических и механических параметров) расхождение в собственных значениях, определенных по двум моделям (с фиксацией угла ψ на торцах и без такового), невелико. Тем не менее качественное расхождение – верное: фиксация угла ψ на торцах делает балку более жесткой, что отражается в повышении величин собственных частот.

Таблица 2

Частоты колебания шарнирно-опертой балки

Номер моды	Торцы со свободным сдвигом	Решение в пакете COSMOS/M	Торцы с фиксированным сдвигом
1	146,271	146,058	146,308
2	567,477	564,397	568,005
3	1 218,091	1 204,820	1 220,416
4	2 040,959	2 006,992	2 047,117
5	2 982,133	2 915,593	2 994,430

Параметры инерции балки в данном случае для прямоугольного сечения с шириной b и высотой h определяются следующим образом:

B _p=p -h , C p = 0, D _p =p —

Рассмотрим трехслойную балку с податливым заполнителем. Решим задачу о ее собственных колебаниях. Назначим следующие геометрические параметры: длина – 1 м, толщина несущих слоев – 1 мм, толщина слоя заполнителя – 3 см. Материал несущих слоев – сталь (Е = 210 ГПа, μ = 0,28, ρ = 7 700 кг/м3). Изотропный материал заполнителя обладает модулем сдвига Gзап = 2,9 МПа. С помощью программы [6] получены результаты решения задачи на собственные значения при ширине сечения в 1 мм (табл. 3). Параметры инерции трехслойной балки вычисляются по формулам

Bp=(2Ph h, +Рз h)b , Cp= 0, л (pн(H3-h3)+pзh3) b2, где ρн и ρз – плотности материалов несущих слоев и заполнителя; hн и hз – толщины несущих слоев и слоя заполнителя; H – общая толщина пакета, H = 2 hн + hз.

Таблица 3

Частоты колебания трехслойной шарнирно-опертой балки

Номер моды	Торцы со свободным сдвигом	Решение в пакете COSMOS/M	Торцы с фиксированным сдвигом
1	20,99	20,388	21,220
2	43,304	42,278	43,805
3	65,346	64,473	66,119
4	87,312	87,22	88,341
5	109,248	111,049	110,555

Для сравнения приводится результат (табл. 3, третий столбец) решения задачи в пакете COSMOS/M, где трехслойная конструкция моделировалась элементами PLANE2D (заполнитель) и BEAM2D (несущие слои).

Хорошее совпадение частот собственных колебаний (табл. 3), вычисленных с помощью двух разных моделей, подтверждает правильность разрабатываемого нами подхода. Здесь же приводятся результаты расчета для модели с фиксированным сдвигом на торцах (см. табл. 3, четвертый столбец). Небольшое отличие частот для балок с фиксацией сдвига и без такового характерно для граничных условий шарнирного опирания.

Выполнен модальный расчет трехслойной конструкции в пакете COSMOS/M с моделированием балки элементами слоистой пластины SHELL4L. На торцах – условия шарнирного опирания: слева – неподвижный шарнир, справа – подвижный в направлении продольной оси. Ширина сечения балки – 50 мм. Остальные размеры и механические свойства материалов такие же, как в балке предыдущего расчета.

Результаты расчетов (табл. 4) сравниваются с данными, определенными по нашей модели. Как видим, имеется заметное расхождение, что свидетельствует о том, что в модели пакета COSMOS/M не учитываются рассматриваемые нами эффекты. В данном случае большего доверия заслуживают наши результаты, поскольку они почти точно совпадают с решением, полученным в том же пакете COSMOS/M при строгом моделировании поведения заполнителя (см. табл. 3).

Рассмотрим трехслойную балку с граничными условиями жесткого защемления торцов.

при x = 0 и при x = L: w = 0, u = 0, ψ = 0, dw/dx = 0. (15)

Сохраним геометрические параметры предыдущей задачи: длина – 1 м, толщина несущих слоев – 1 мм, толщина слоя заполнителя – 3 см, ширина сечения – 1 мм. Материал несущих слоев – сталь (Е = 210 ГПа, μ = 0,28, ρ = 7 700 кг/м3). Модуль сдвига изотропного материала заполнителя примем Gзап = 290 МПа.

Таблица 4

Частоты колебания трехслойной полосы

Номер моды	Торцы со свободным сдвигом	Решение в пакете COSMOS/M (SHELL4L)
1	20,964	22,227
2	43,292	46,028
3	65,338	69,487
4	87,306	92,829
5	109,243	116,097

Рассмотрим результаты решения задачи (табл. 5). Для сравнения приводятся частоты (см. табл. 5, третий столбец), вычисленные с помощью пакета COSMOS/M, где трехслойная конструкция моделировалась элементами PLANE2D (заполнитель) и BEAM2D (несущие слои). Защемление торцов обеспечено фиксацией угловых узлов на краях. Вновь следует отметить весьма хорошее совпадение и в количественном (табл. 5) и в качественном отношении результатов, полученных по нашей модели и в пакете COSMOS/M.

Выполнен модальный расчет для балки с защемленными торцами, на которых, однако, освобожден угол сдвига. Значения частот собственных колебаний показаны в предпоследнем столбце табл. 5. Они существенно расходятся с соответствующими величинами, вычисленными для жестко защемленной балки (табл. 5, второй столбец). Следовательно, в модальном расчете балки со вторым видом защемления для точного определения частот и форм собственных колебаний требуется рассматриваемая в нашей работе модель (постановка).

Для сравнения выполнено решение задачи для балки с шарнирным опиранием торцов, где, кроме того, допущен сдвиг (см. табл. 5, последний столбец). Как видим, результаты отличаются от тех, что получены для защемленной балки со свободным сдвигом на торцах.

Последнее решение задачи об определении частот собственных колебаний защемленной (со свободным сдвигом на торцах) трехслойной балки выполнено для весьма податливого заполнителя G зап = 2,9 МПа. Получены следующие величины пяти первых частот: f 1 = 21,262 Гц, f 2 = 43,833 Гц, f 3 = 66,136 Гц, f 4 = 88,365 Гц, f 5 = 110,567 Гц. Сравнивая эти значения с частотами колебания шарнирно-опертой балки со свободным сдвигом на торцах (см. табл. 4), можно заключить, что в случае достаточно малой жесткости балки при трансверсальном сдвиге защемление торцов со свободным сдвигом можно моделировать шарнирным опиранием (тоже со свободным сдвигом).

В заключение выполним модальный анализ монолитной балки, изготовленной из однонаправленного композита, например углепластика, у которого следующие актуальные для данной задачи механические свойства: Е = 180 ГПа, G = 5 ГПа и плотность ρ = 1500 кг/м3. Выполним серию расчетов для различных вариантов граничных условий. Получены резуль- таты этих вычислений в виде первых пяти частот соб ственных колебаний (табл. 6).

Таблица 5

Частоты колебания трехслойной балки, защемленной по торцам

Номер моды	Жесткое защемление торцов	Решение в пакете COSMOS/M	Защемление со свободным сдвигом на торцах	Шарнирно-опертые торцы со свободным сдвигом
1	134,105	130,53	77,563	70,122
2	309,411	298,818	254,025	245,059
3	518,337	497,572	477,927	467,133
4	742,287	710,749	716,150	703,270
5	972,990	931,689	956,270	941,120

Таблица 6

Частоты колебания многослойной балки при различных вариантах закрепления торцов

Номер моды	Шарнирно-опертые торцы со свободным сдвигом		Шарнирно-опертые торцы с фиксированным сдвигом	Защемление торцов
	Авторская модель	COSMOS/M		фиксированный сдвиг	свободный сдвиг
1	49,598	49,587	49,599	111,787	96,267
2	197,494	197,335	197,521	305,515	269,699
3	441,062	440,279	441,197	592,381	533,552
4	776,122	773,732	776,538	966,163	884,950
5	1 197,208	1 191,62	1 198,192	1 420,876	1 319,846

Как и в предыдущих примерах, здесь рассматривались следующие варианты граничных условий: классическое шарнирное опирание со свободным трансверсальным сдвигом на торцах, шарнирное опирание с фиксацией сдвига на торцах, жесткое защемление торцов, защемление со свободным сдвигом на торцах.

Здесь же приведены данные расчета, выполненного для балки с классическим шарнирным опиранием в пакете COSMOS/M, где монолитная композитная конструкция, колебания которой происходят в одной плоскости, моделируется элементами PLANE2D.

Как следует из представленных значений (см. табл. 6), имеется хорошее совпадение данных нашего расчета с результатами вычислений, выполненных в пакете. Напомним, что наше решение соответствует одномерной балочной модели, а расчеты в пакете COSMOS/M проводились с помощью двумерной модели, чтобы адекватно учесть поведение конструкции с низкой трансверсальной сдвиговой жесткостью.

Анализ представленных данных (см. табл. 6) подтверждает ранее сделанный вывод о том, что в общем случае модальный расчет композитных балок с неклассическими граничными условиями (шарнирно-опертые торцы с фиксированным сдвигом и защемление со свободным сдвигом на торцах) приводит к результатам, отличным от тех, которые получаются при классических вариантах этих граничных условий. Это обстоятельство подчеркивает актуальность разработанной модели.

В заключение сформулируем выводы.

• 1.    Получен энергетический функционал для решения задачи о собственных колебаниях балок с низкой трансверсальной жесткостью.

• 2.    Разработана конечно-элементная модель податливой при сдвиге балки, вектор узловых неизвестных которой включает углы трансверсального сдвига. Сформированы матрица жесткости и матрица инерции для соответствующего балочного элемента.

• 3.    В результате проведенного численного исследования на примере расчета изотропных, ортотропных композитных и трехслойных балок показана актуальность разработанной модели при проведении модального анализа конструкций с низкой трансверсальной сдвиговой жесткостью, а также при учете граничных условий неклассического вида.