Модель адсорбционной очистки стоков с учетом химической реакции

EDN: LQRBCY

В работе ставится общая задача динамики адсорбции целевого компонента из жидкости в условиях протекания химической реакции первого порядка при линейной изотерме адсорбции.

Имеющиеся в литературе решения [1-3], представленные различными функциями, не всегда могут быть быстро доведены до числовых инженерных расчетов, вследствие громоздкости полученных результатов.

Поэтому здесь поставлена цель - от постановки задачи до получения числового результата дойти путем алгоритмизации полученного решения и его программирования.

Известно, что согласно теореме о единственности решения, при корректной постановке задачи на результат не влияет метод решения, но форма представления может быть различной.

Рассматриваемая нами модель адсорбции в неподвижном слое адсорбента базируется на уравнениях баланса массы целевого компонента для бесконечно малого элемента слоя и кинетики адсорбции, записанных в частных производных (система уравнений в частных производных).

В этой связи для интегрирования системы линейных дифференциальных уравнений в частных производных первого порядка был выбран метод преобразования Лапласа. Он позволил перейти от совместного решения системы уравнений в частных производных первого порядка к независимому решению в изображениях задачи Коши для обыкновенного дифференциального уравнения первого порядка и алгебраического уравнения. При этом удалось получить результат в широко используемых в математической физике хорошо изученных и табулированных функциях Бесселя.

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ

Система дифференциальных уравнений адсорбции в одномерном потоке без учета продольной диффузии имеет вид [4-6]

сССхГ + g 5Ca(x,т) + W 9C(x,т) = дт         дтд

= - KC (x ,T), x > 0, т > 0,

• д Ca* x,T) = K [c (x ,т) - C •( Ca )J

дт x > 0,т > 0.

при краевых условиях

C(x,0) = 0, x > 0,

Ca (x,0) = 0, x > 0,

C(0,т) = C0, т > 0.

Уравнение изотермы

Ca (x ,T) = AC (Ca ).

Здесь C a ( x, т ) - концентрация адсорбированного вещества в сорбенте в сечении x в момент времени т ; C ( x , т ) — концентрация адсорбтива в потоке на расстоянии x в момент времени т ; W - постоянная скорость потока;

1 - £

K - коэффициент массообмена; 5 =--- -

£ коэффициент; £ - доля свободного сечения в адсорбенте (постоянная по объему порозность неподвижного слоя); C (Ca) - концентрация целевого компонента в потоке равновесная со средним содержанием адсорбтива в слое.

Первые два слагаемых уравнения (1) представляют собой скорость изменения массы целевого компонента в зазорах между частицами и внутри частиц соответственно. Третье слагаемое соответствует приращению количества целевого компонента за счет конвективного переноса со скоростью потока. Слагаемое в правой части (1) представляет изменение концентрации целевого компонента в потоке в момент времени в сечении x за счет химической реакции.

Таким образом, уравнение (1) представляет связь между концентрациями целевого компонента в неподвижном слое адсорбента и в потоке в любой момент времени т и в любом сечении x слоя.

Краевые условия (3)-(5) означают следующее. В начальном сечении слоя ( x = 0 ) в любой момент времени т концентрация целевого компонента постоянна и равна C 0 , в начальный момент времени при т = 0 слой адсорбента свободен от адсорбируемого вещества: условия (3),(4).

С учетом (6) уравнения (1), (2) преобразуются к виду дC(x-т) + W8C(x-т) = -5K х дт          дx

С ( x, т )

X C ^{( xт ) -} a^T"

- K c C ( x , т ),

(1а)

x > 0,т > 0, д C,( x,т) = K C (x ,т) - ККГ. дт                  A

(2а)

x >  0, т >  0.

К уравнениям (1а), (2а) и граничным условиям (3) - (5) применяется прямое преобразование Лапласа [7-9]

да

C ( x, т )o—. f ( x , 5 ) = j C ( x, т )e^^srdT,

C a ^{( x, т} )

дC(x,т) дт д Ca ( x ,т ) дт

Здесь знак

^

Ф (x, 5) = j Ca (x, т )e -sTd^T, s F (x, s ) - C (x ,0),

5 Ф ( X , 5 ) - C a ( X ,0).

обозначает переход от ориги- нала к изображению.

Тогда преобразование (1а), (2а) с учетом граничных условий (3) - (6) будет давать sF (x, s ) + W дF (x, s ) = дx

• - ( 6 K + K c ) F ( X , 5 ) + ^ K Ф ( X , 5 ), c A

Ф ( x , 5 ) =   ^AK  F ( x , 5 ),

AS + K

F (0, s ) = C ⁰.

s

Дальнейшее преобразование уравнений (11), (12) с учетом (13), приводит к задаче Коши для обыкновенного дифференциального уравнения первого порядка dF(^, 5 ) + Ax F ( x, ^) = 0, dx

F (0, s ) = C 0 , s

s где A, = W +

5KsK

---------------------------1-- .

(s + K )W

A

Решением (14), (13) будет функция

F ( x , s ) = C 0 e " A ^{1 x} .

s

KC _oexp l-

Подстановка (15) в соотношение (12) приводит к выражению

Ф ( x , 5 ) = KCK e" A ^{1 x} .

S ( 5 + —) A

Замена в (15), (16) константы A ₁ , её значением позволяет получить

F ( x , s ) =

к

Co

= ¹¹ exp

s

^^^^^^^в

s

+ W

§ K s

V

W s + ^K

A

K

+ —

W

KC

Ф ( x , 5 ) =----- °— X

K

^{5 ( 5 + )}

A

x

к

, (17)

^X exp

в

s

--+

W

§ K s

V

W s + ^K

A

K

+ -

W

x

.

( K s s +

к A

x I

s

W )

^—- exp

X exp

^^^^^^^в

AW ( K

1 S +

K² § x к A

⁽ 8 K ⁺ K c )W .

X

(18а)

Для получения оригиналов от (17а) и (18а) необходимо продолжить их преобразование

Известно соотношение [9]

f ( s ) =

~4уexp s + A J

F ( т ) =

^^^^^^^в

AW

^ K² 5 x

( г

X J i 2

к

AW ( K

I s +—

K 2 5 x V A

_   ( K

тexp - -т x

I A J

K ² 5 x

.3---------т

N AW J

.

В соотношениях (17), (18) необходимо образовать экспоненциальную функцию получения таблицы изображений

пре-для

Выражение (19) будет являться базовым в процессе преобразования (17а), (18а) к табличному виду.

Тогда (17а), (18а) следует переписать в виде

к

I x C_n exp-- s ⁰

F ( x , s ) =---- ^W_

exp

в

s

--+

W

5 K

W

V

sK 1

s + ^K W

A

I x I

= ^exp | -— ^s I exp

V W 7

K 2 5 x

s

, K V s + I x

A 7

x

X

Kexp s + A J

в

AW ( K 1 s +

K 2 5 x V A

X

^X exp

в

AW ( s + K )

( 5 K + K_c ) — . c W

X

^X . K ⁺ K c ) W ,

(17б)

Тогда преобразование (17), (18) дает

( x

KC_n exp-- 5

0 I W

Ф ( X , 5 ) =------ ^-W-

s

. K I

5 + — X

A J

F ( x , 5 ) =

^C o ^exp |" il ^s I ---L W J exp

X

s

AW ( K 1 s +

K 2 5 x V A

X

K  exp s+A J

в

X exp

" ^{( 5 K +} K c ) W ,

(17а)

AW ( K 1 s +

K 2 5 x V A

^X exp ( 5 K ₊ K c )W .

Ф ( X , 5 ) =

X

(18б)

И, наконец, окончательно преобразуется выражение (17б) путем возведения в квадрат круглой скобки, стоящей в числителе

x exp

^^^^^^^B

AW

K ²5x

x

F ( x , 5 ) = C 0 <

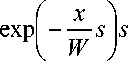
K

5 + A

-^exp

⁵ + A J

^^^^^^^B

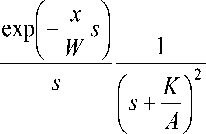
exp

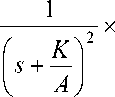
₃ K    I X I

+ 2—exp-- 5 x

A   I W J

AW

K ² 5 x

+

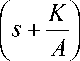
K ²

A ^{2 X}

AW I K5 1 5 + I

K²5x (    A J

^X_;p - K + K c ) Wx .

> x

(17в)

Для перехода к оригиналу от соотношения (17в) требуется найти оригиналы 3-х отдельных его составляющих, входящих в виде суммы в фигурную скобку.

Для этого следует сначала найти ещё один табличный оригинал [7]

exp ( - as )

О при 0 <  t <  a ,

s

1 при a <  t ,

который применительно к нашему случаю, бу-

дет иметь вид

f . ( 5 ) =

( x )

exp-- 5

к W )

s

FT) = ^

x

О при 0 <  т <  —, W

x

1 при — <  T .

W

Следует отметить, что нахождение оригиналов от каждого из 3-х суммируемых изображений в фигурной скобке выражения (17в) производится по разному. Оригинал третьего члена находится простой сверткой оригиналов.

Известно, что произведению изображений соответствует своеобразная интегральная комбинация оригиналов функций, то есть f.( 5 ) f,( 5 ) — F(T )* F2(T ) =

= j F₁ ( t) F₂ ( t - t) dt = j F₁( t - t) F₂ ( t) dt . 0                           0

Тогда применительно к третьему члену выражения (17в) на основании формул (19), (20) можно получить f ( 5 ) f1( 5 ) — F (t )* F1(T ) = F (t)*1 =

T

=j

x

AW

^ K2dx

t exp l

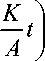
x

W

x J ₁

к

2 K"^Sx_t}

J

dt .

Ко второму члену выражения (17 в ) применя ется первая теорема смещения [7]

F ( t - a ) c^> exp( - a 5 ) f ( 5 ) .

В обозначениях статьи согласно (19) это дает

x f2(5) = expl - W5 If(5)

F 2 ( t ) =

AW <  x ) l т I K ²5x к   W )

x J ₁

exp

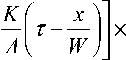
K ² § x

AW

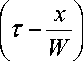
Следует подчеркнуть, что при т <  — дей- ^W

ствительное решение задачи отсутствует. Это видно, в частности, из соотношения (22).

При поиске оригинала для первого члена в соотношении (17в) сначала применяется теорема о дифференцировании оригинала [4]

F '( т )^ 5f ( 5 ) - F ( + 0) .

В соответствии с этой записью, представленными в статье обозначениями, формулами (17в) и (19) должно быть записано

= F '( т ) — sf ( s ) - F ( + 0). d T

Согласно соотношению (19) F ( + 0) = 0

d J AW dT ^ K ²5x

t exp |

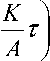
x

/

и

x J ₁

к

2 K^xt

V AW

)

^{sf ( s )}.

(23а)

Дифференцирование левой части (23а) после необходимых преобразований приведет к зависимости

sf ⁽ s ⁾

( K „A exp" 7r)

J о ²

V

K 25x

AW

-

K AW „ K² 5 x J 2J

A\K² § x ¹ N AW

V

T

V

τ

V

-

Теперь к выражению (24) применяется первая теорема смещения [7] после умножения его ( ^x . правой части на exp -    5

I W

Тогда будет exp|-—s |sf (5) • F| т - — | = exp I W J I W J

K --x

A

f K.

x exp-- 1 J, 2

V A V 1

^x exp

V

K ²5x

AW

t dt

V

1 x

( 5 K + K_c )— c W

AW

\ K² 5 x

_ K² 5 x f x A

2 ----------1 т--I

V AW V WV

× A

Для доведения выражений (26), (27) до числа необходимо численным методом найти один и тот же интеграл, входящий в оба выражения. Поэтому для рационализации вычислений можно выполнить небольшое преобразование на основе дифуравнения (2а).

Для этого следует подставить в правую часть (2а) решения (26) и (27). Тогда после необходимых математических операций можно получить 5Ca.(x,т) = K\с(x,т)-Ca^x^^) 1 = KC0 X от L           A

×

K ² 6 x f    x A

1 T I AW V   W V

. (25)

^{x ex}p

K ²5x

AW

×

Таким образом на основании (17в), (21), (22),

x exp

( 5 K + K_c )— c W

(25) получено

F ( x , s ) —° C ( x , т ) = C ₀ ^ exp

-

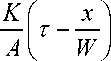
K

-

A

Откуда

C ⁽ x , ^т ) = C a ⁽ Ax ^{, T} ) + C 0 exp

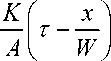
x J о

×

₂ K ^

AW

x τ -

W

K

+ a ^exP

x τ -

W

×

^x J 0

K ² § x

AW

×

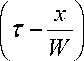
AW f xV

τ- J

K2 5 x V   WV 1

k ² f

+ A? J x

W

AW

—5— t exp l

K ² S x     ¹

^x exp

K ² S x

AW

+

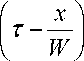
₂ K ^

N AW

V

( 5 K + K )— c W

Л

t dt

1 x

V

Аналогичным образом на основе (18б) осуществляется переход к оригиналам с использованием тех же методов, теорем и таблиц изображений, приведенных выше.

Было получено

Ф ( X , S ) ^C a ( X ,T) =

^x exp

( 5 K + K_c )— c W

Кстати, можно отметить, что, если взять производную от (27) по времени, то в точности получится выражение (28), что подтверждает правильность полученных решений.

Таким образом, результаты решений могут быть доведены до числа по следующему алгоритму:

- вычисляется C a ( x, т ) по выражению (27);

- вычисляется концентрация C ( x, т ) по выражению (29).

Полученные результаты решения исходной задачи полностью подготовлены к программированию на любом алгоритмическом языке высокого уровня.

x J ₁

= KC о

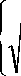
AW

K ² 6 x

K ² S x

AW

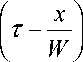
exp

x τ-

W

×

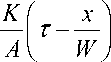
AW

ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ

+ ^{K τ}

⁺ A ^J A/ K² S x x

t×

Результаты решения позволили разработать алгоритмы и выполнить программирование задачи для получения численных результатов.

Далее выполняется расчет концентраций C ( x, т ) и C a ( x, т ) в адсорбции хлороформа

W

при очистке сточных вод плавательного бассейна цеолитами Татарско-Шаршатранского месторождения Татарстана. Использовались следующие исходные характеристики цеолитового слоя, состоящего из гранул диаметром 4,69 мм.

Истинная плотность гранул, р _и = 2.26 г / см ³ ; кажущаяся плотность слоя цеолита, р _к = 1.2 г / см ³ ; насыпная плотность гранул цеолита в слое, р _н = 0.71 г / см ³; порозность слоя цеолита, 5 = 0.41; коэффициент A =36.4; W =0.00011м/с [10] ; C ₀ = 15мг/л; K = 0.0004351 м/с; K c = 0.0001 м/с.

Результаты расчетов представлены на рисунках 1 - 2.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

На рисунках 1 и 2 представлены графики изменения концентраций хлороформа в адсорбенте и адсорбтиве в зависимости от расстояния x от входа в слой цеолита при фиксированном времени, т .

Значения концентрации C ( x , т ) , как и ожидалось, уменьшаются, а C a ( x, т ) сначала увеличиваются, а затем уменьшаются вдоль координаты x . Причем, согласно условиям (4), (5) должно быть: при x >  0 , т ^ 0 концентрация C a ( x ,0 ) ^ 0 , а при т >  0 , x ^ 0 концентрация C ( 0, т ) ^ 0 , что в действительности и имеет место.

Решения (26), (27), именно, стремятся к нолю соответственно при т ^ 0 и x ^ 0 , а не точно равны нолю. Такие свойства обычно имеют решения, полученные при использовании метода преобразования Лапласа.

В самом деле, решения пригодны при x т > — и фактически граница времени (значит и граница решения) при постоянной W и различных x перемещается в зависимости от x , в x то время как при т -^ значения концентраций уже становятся равными нолю, но не точно при x = 0.

Поэтому на графиках рисунка 1 концентрация C ( 0, т ) обозначена согласно граничному условию равной C 0 ,а при т >  0 концентрация C a ( x ,0 ) обозначена равной нолю.

Другими словами, нисходящая ветвь кривой концентраций C ( x, т ) , как и должно быть, представлена точно выходящей из точки C ( 0, т ) = C 0 , хотя координата x не равна нолю, а восходящая ветвь концентраций C a ( x , т ) исходящей из точки C a ( x ,0 ) = 0 , хотя время т не равно нолю (условно обозначена пунктиром).

Следует отметить, что вне зависимости от времени характер изменения концентраций на обоих графиках не изменяется, хотя числовые значения величин различны. Также очевидно, что при малых исходных значениях концентраций, которые представлены в статье, концентрация адсорбтива вначале резко уменьшается (сильно отличается от C ₀ ), а затем плавно во всем диапазоне изменения x незначительно уменьшается.

Иными словами, слой цеолита даже небольшой толщины может в течение длительного времени работать в этих условиях, практически

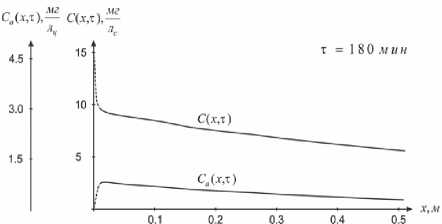
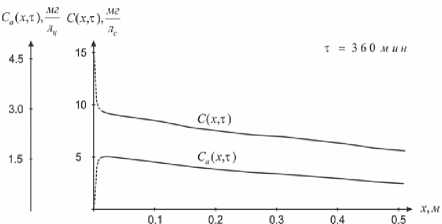
Рис. 1. Изменение концентрации адсорбтива и адсорбата в зависимости от координаты x при фиксированном времени t

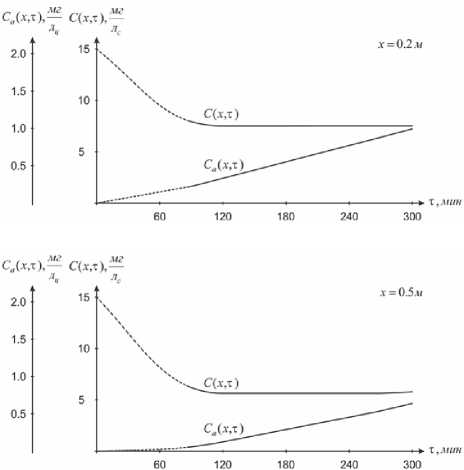
Рис. 2. Изменение концентрации адсорбтива и адсорбата в зависимости от времени t при фиксированном расстоянии x

не изменяя адсорбционных свойств: схождение ветвей кривых С ( x, т ) и C a ( x, т ) - невелико.

На рисунке 2 представлены графики изменения концентраций целевого компонента в адсорбтиве и адсорбенте при фиксированных значениях x . При построении этих графиков также учитывались вышеотмеченные нюансы, касающиеся графиков на рисунке 1. Поэтому приведенный в них результат понятен, очевидно, и без комментариев.

ЗАКЛЮЧЕНИЕ

Из вышеприведенных рассуждений очевидно, что применение методик приемов и теорем метода преобразования Лапласа дало возможность глубоко вникнуть в суть задачи, что не доступно при других методах решения.

Использование метода преобразования Лапласа позволило найти решение задачи адсорбции в новой форме посредством сведения системы двух взаимосвязанных уравнений к системе независимых уравнений и их решению.

Полностью решена практическая задача, от постановки до получения числового результата, по адсорбции хлороформа при очистке стоков плавательных бассейнов. Это позволяет при известном наборе исходных данных по детально разработанному алгоритму, реализованному в виде программы на языке высокого уровня, найти изменение концентраций целевого компонента в обеих фазах и подобрать толщину слоя адсорбента.