Модель анализа надежности распределенных вычислительных систем

Характерной особенностью многих клиент-серверных приложений (КС-приложений) современных распределенных вычислительных систем является их разнородность и рассредоточенность. При проектировании распределенных вычислительных систем имеется ряд специфических особенностей. Это, в первую очередь, зависимость архитектурной модели от ряда нефункциональных системных требований, например, производительности, защищенности, безопасности, надежности [1]. При анализе архитектурных решений в рамках современных систем существенное значение для разработчика имеет возможность оценки архитектурной надежности КС-приложений как важной составной части системы [2].

Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение

В распределенной вычислительной системе, кроме того, разные системные компоненты могут быть реализованы на разных языках программирования и выполняться на разных типах процессоров. Модели данных, представление информации и протоколы взаимодействия не являются однотипными в распределенных системах, поэтому архитектурная надежность является немаловажным фактором при проектировании [3]. Как правило, промежуточные составляющие формируются из готовых компонентов и не требуют от разработчиков специальных доработок.

В архитектуре «клиент-сервер» серверная часть, как правило, устанавливается на отдельном компьютере-сервере, а клиентские части программного обеспечения (ПО) на рабочих местах, причем функциональный состав ПО – на рабочих местах различен. Серверная и клиентские части ПО могут функционировать в различных операционных средах. В связи с этим важной и актуальной является проблема анализа надежностных характеристик распределенных вычислительных систем с клиент-серверной архитектурой.

Математическая модель анализа распределенных вычислительных систем клиент-серверной архитектуры. Предполагаем, что рассматриваемая система функционирует в нормальных (не граничных) условиях, поэтому можно допустить независимость отдельных отказов. В предлагаемой модели подсистемы невосстанавливаемые.

Под распределенной вычислительной системой (РВС) будем понимать совокупность аппаратных и программных средств, реализующих следующие основные функции [4]: обработку, хранение, передачу и защиту данных. Структура вычислительной системы представлена на рис. 1, где сервер – это элемент, включающий в себя систему хранения данных (СХД) со своими системой передачи даны (СПД) и системой безопасности (СБ), клиент – элемент системы, содержащий систему обработки данных (СОД) со своими

СПД и СБ, а концентратор служит для связи клиентов и сервера и состоит из СПД и СБ [5]. Будем рассматривать систему с N клиентами и одним сервером.

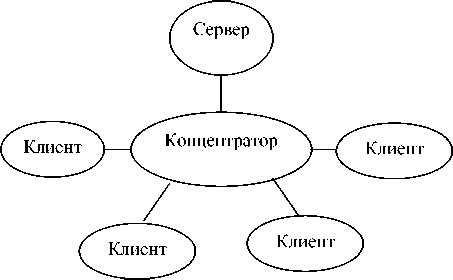
Рис. 1. Структура распределенной вычислительной системы с радиальной структурой

Можно выделить следующие виды отказов системы безопасности: скрытый и ложный [6]. При скрытом отказе СБ не парирует отказы остальных подсистем, при ложном СБ самопроизвольно вырабатывает защитные функции при нормальной работе СХД, СОД и СПД и приводит к останову системы.

Основным показателем надежности будем считать вероятность потери данных за определенный интервал времени. Под потерей данных будем понимать реальное уничтожение или утечку данных либо невозможность в течение достаточно длительного интервала времени получить доступ к ним.

Описание математической модели. На рис. 2 приведена графическая модель функционирования распределенной вычислительной системы, отражающая отказы ее подсистем и дальнейшее развитие ситуаций. Сплошными линиями обозначены переходы элементов, штриховыми – развитие ситуаций отказов элементов.

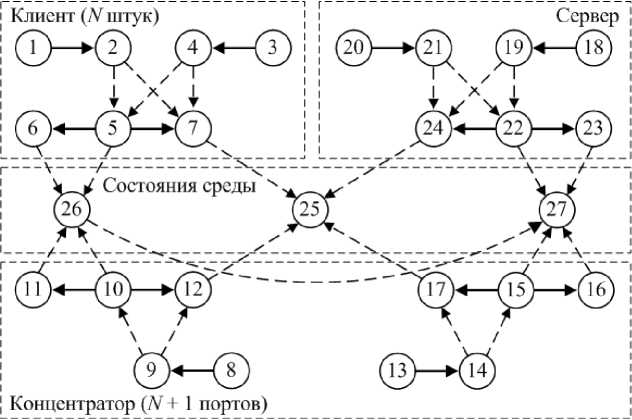
Рис. 2. Графическая модель функционирования распределенной вычислительной системы

Состояния в графе означают следующее: 1 – нормальная работа СОД; 2 – отказ СОД; 3 – нормальная работа СПД клиента; 4 – отказ СПД клиента; 5 – нормальная работа СБ клиента; 6 – ложный отказ СБ клиента; 7 – скрытый отказ СБ клиента; 8 – нормальная работа СПД порта концентратора, к которому подключен клиент; 9 – отказ СПД порта концентратора, к которому подключен клиент; 10 – нормальная работа порта СБ концентратора, к которому подключен клиент; 11 – ложный отказ СБ порта концентратора, к которому подключен клиент; 12 – скрытый отказ СБ порта концентратора, к которому подключен клиент; 13 – нормальная работа СПД порта концентратора, к которому подключен сервер; 14 – отказ СПД порта концентратора, к которому подключен сервер; 15 – нормальная работа порта СБ концентратора, к которому подключен сервер; 16 – ложный отказ СБ порта концентратора, к которому подключен сервер; 17 – скрытый отказ СБ порта концентратора, к которому подключен сервер; 18 – нормальная работа СХД; 19 – отказ СХД; 20 – нормальная работа СПД сервера; 21 – отказ СПД сервера; 22 – нормальная работа СБ сервера; 23 – ложный отказ СБ сервера; 24 – скрытый отказ СБ сервера; 25 – состояние аварии РВС; 26 – состояние сниженной эффективности РВС; 27 – состояние останова РВС.

При отказе СОД или СПД на клиенте либо отказе СПД порта концентратора, к которому подключен клиент, при нормально работающей соответствующей СБ клиент или порт концентратора переходит в состояние останова, а сама система – в состояние сниженной эффективности (как и при ложном отказе СБ клиента или порта концентратора, к которому подключен клиент). При отказе СХД или СПД сервера или СПД порта концентратора, к которому подключен сервер, при нормально работающей соответствующей СБ распределенная вычислительная система переходит в состояние останова, как и при ложном отказе СБ сервера или порта концентратора, к которому он подключен, а также при останове всех клиентов или портов концентратора, к которым подключены клиенты. При отказе любой из подсистем при скрытом отказе отвечающей за ее контроль СБ система переходит в состояние аварии.

Будем рассматривать поведение системы на интервале [0, t ]. Введем необходимые обозначения. Пусть ψ – наработка до отказа СОД, имеющая распределение f _ψ( t ) = P (ψ ≤ t ); δ – наработка до отказа СХД, имеющая распределение F δ ( t ) = P (δ ≤ t ); γ 1 , γ 2 , γ 3 – наработки до отказа клиента порта концентратора и сервера соответственно, имеющие распределения F γ1 ( t ) = P (γ 1 ≤ t ), F γ2 ( t ) = P (γ 2 ≤ t ), F γ3 ( t ) = P (γ 3 ≤ t ).

Обозначим через ρ 1 , ρ 2 , и ρ 3 наработки до скрытых, а через η 1 , η 2 и η 3 наработки до ложных отказов СБ клиента, порта концентратора и сервера соответственно с распределениями

F p1 (t ) = P ( p 1 <  t ), F _p 2 ( t ) = P ( p ₂ <  t ),

F _p 3 ( t ) = P ( р з <  t ), F _n 1 ( t ) = P ( n <  t ), ^F n2 ⁽ t) = ^{р (} П ₂ <  t ), ^F _{4 3} ⁽ t) = ^{р (} П з <  t ^).

Показатели надежности. Под показателями надежности подразумеваются вероятности перехода системы в состояния останова и аварии, а также интенсивности этих переходов [7; 8]. Вначале рассмотрим показатели надежности, относящиеся к переходам в состояние останова.

Останов распределенной вычислительной системы наступит, если в состояние останова перейдут все клиенты или все порты концентратора, к которым подключены клиенты, сервер или порт концентратора, к которому он подключен.

Вероятность того, что на интервале [0, t ] произойдет останов, можно записать следующим образом:

Po (t) = 1 - M(Poki (t)Pok2 (t)Pok3 (t)Poc (t)), где Pок1(t) – вероятность останова всех клиентов к моменту времени t; Pок2(t) – вероятность останова всех портов концентратора, к которым подключены клиенты, к моменту времени t; Pок3(t) – вероятность останова порта концентратора, к которому подключен сервер, к моменту времени t; Pос(t) – вероятность останова сервера к моменту времени t.

Введем вспомогательные переменные . Пусть ζ i – время до останова i -го клиента, где i = 1, N . Тогда вероятность того, что на интервале [0, t ] произойдет останов верх клиентов, определяется выражением

Г N.      ^

P >ki ( t ) = ^P\ vC <  t I ,

I i = 1             j

N где v Zi = max(Z1,Z2, ..., Zn)

• i = 1

Используя свойства индикаторов и математического ожидания, получим

N

P oк1 (.t ) = MI n    = M П I Zi< t =

• v Z i < ti

i = 1

NNN

=П miZi< t = П p (Zi < t)=П (1 - Pi ок (t)), i=1                     i=1

где P i oк ( t ) – вероятность того, что останов i -го клиента не произойдет к моменту времени t ; I ζi ≤ t – функция-индикатор ( I ζi ≤ t = 1 при ζ i ≤ t и I ζi ≤ t = 0 при ζ i > t ).

Вероятность того, что i -й клиент к моменту времени t не перейдет в состояние останова:

рЮк (t) = P(Ipn^i^Yn^i A Y1i ЛПп + Ipu t)), где Vi AY1i = min(Vi, Y1i).

Проведя ряд аналитических преобразований, получим p ок (t) = Fn1i( t )((1 - Fp1i(Wi) Fpu(Y1i)) x

• X F v ( t ) Fy_u( t ) + F p _h( V i ) F p„ ( Y 1 i )).           (1)

Пусть τ j – время до отказа j -го порта ко нце нтратора, к которому подключен клиент, где j = 1, N . Вероятность того, что на интервале [0, t ] произойдет останов всех портов концентратора, к которым подключены клиенты, определяется выражением

Рок 2( t) = P [у - < t | = MIn=

\ j=1       J        v - i < t j=1

= M П I - j <, II MI- j < = j=1

=П Pj t)=П (1 - P, (t)), j=1

_X . Л (1 - ^Fnu ( t ) х ((1 - ^MFP_U ( V i ) ^MFP_U (Yu )) F i ( t ) +

^X .   ' ¹           + MFp_ti( V )MFp_u(Yu)))

^{X F 1}1 2( N + 1) ^{( M}F Y 2( N + 1) ^{( p} 2( N + 1> ) ^F Y 2( n + 1) ⁽ t ) ⁺ + ^MF P 2( N + 1) ( Y 2( N + 1) )) ^t ) X X ((1 - MF p _з ( 5 ) MF p _з ( Y з )) F 5 ( t ) F ( t ) + MF p _з ( 5 ) MF P 3 ( Y з ))).

где Р , _т ( t ) - вероятность того, что останову j -го порта концентратора не произойдет к моменту времени t . Р , _т ( t ) можно записать следующим образом:

P j - ⁽ t ) = ^{P (} I _P2_J>-Y2_j ⁿ 2j ^1 2j + I P2_J] ⁿ 2j >  t ) =

= F j t )( F ^) ^Д t ) + ^F P 2 j ( Y 2 _У» (2)

Аналогично можно записать вероятность того, что на интервале [0, t ] не произошел останов порта концентратора, к которому подключен сервер:

Теперь найдем зависимость интенсивности остановов от времени, которую обозначим оо(1):

^ПЛ t ) =

dP _o( t )/ dt 1 - P o ( t )

.

^Р окз ( t ) = ^F N + 1) ( t )( F Y 2( N + 1) < P 2( N + 1) ) F N + 1) ( t ) ⁺

+ ^F P 2( N + 1) ( Y 2( N + 1) )).                    (3)

Вероятность того, что сервер не перешел в состояние останова на интервале [0, t ]:

^р ос ⁽ t ) = ^{р (} I р ₂ >_{5лу з} 5 л у з лп з + I р ₂ <_{5лу з} П з >  t ).

Проделав ряд преобразований, получим:

P ос ( t ) = F 3 ( t )((1 - F p ₃ ( 5 ) F p ₃ ( Y 3 )) F ( t ) F ( t ) +

+ F p 3 ( 5 ) F p 3 ( _Y 3 )).                    (4)

Таким образом, были получены выражения для вычисления вероятности останова и интенсивности остановов распределенной вычислительной системы на интервале времени [0, t ].

Теперь рассмотрим показатели надежности, относящиеся к переходам системы в состояние аварии. Авария произойдет, если в аварийное состояние перейдет хотя бы один клиент, порт концентратора или сервер [9]. Подсистема переходит в аварийное состояние, если после скрытого отказа СБ происходит отказ контролируемых ею подсистем.

Вероятность того, что на интервале [0, t ] произойдет авария, можно записать следующим образом:

P _aK ( t ) = 1 - M ( P _aK1( t ) P _aK 2 ( t ) Р _а с ( t )),

Тогда вероятность того, что на интервале [0, t ] произойдет останов, можно записать следующим об-

разом:

P o ( t ) = 1 - M

1 - П (1 - P ок ( t ))

i = 1

Г N

1 - П (1 - P j - ( t )) Р окз ( t ) Р ос ( t )

Поскольку все отказы независимы, то это выражение можно записать так:

P o ( t ) = 1 -

1 - П (1 - МР ок ( t )) i = 1

X 1 - П (1 - Мр ( t )) МР окз ( t ) МР ос ( t )

Подставив (1), (2), (з) и (4) в (5), получим

P o ( t ) = 1 -

. (5)

Г N                                           )

1 - П (1 - F^ ( t )( M^j ( P 2 j ) х F ( t ) + MF p ( Y 2 j )))

I j = 1                                                             J

х

где P _ак1( t ) - вероятность аварии одного из клиентов к моменту времени t ; P _ак2( t ) - вероятность аварии одного из портов концентратора к моменту времени t ; P _ac( t ) - вероятность аварии сервера к моменту времени t .

Введем вспомогательные переменные. Пусть m i -время до перехода i- го клиента в аварийное состояние, где i е 1, N . Тогда вероятность того, что на интервале [0, t ] ни один клиент не перейдет в аварийное состояние, определяется выражением

Г ^N      )

^Р ак1 ⁽ t ) = ^P\ ^® i >  t I .

k i = 1           J

Выполнив ряд аналитических преобразований, получим

N

P„1(t) = MIn    = MП Imi>t = л m i > ti j'=1

NNN

= П MImi>t =П P(m > t) =П Paki(t), i=1                     i=1

где Р_ак i ( t ) - вероятность того, что авария i- го клиента не произойдет к моменту времени t.

Вероятность того, что i- й клиент на интервале [0, t ] не перейдет в состояние аварии:

Р ак i ( t ) = 1 - P ( P 1 i л t < V i л Y 1 i <  t ).

Отсюда paH(t) =1 -IP1i

Пусть еj - время до отказа j-го порта концентратора, ведущего к аварии РВС, где j е 1, N +1. Тогда ве

роятность того, что ни один из портов концентратора не перейдет в аварийное состояние на интервале [0, t],

_ I rt      FP2( y) dF5 (y) +Y

MPac(t) = 1 - MF (Y3 )L          rt.

Jo + MFY3 (5)J PP2 (y)dF, (y) 3               ■3

определяется выражением

Pa 2( t) = PI Na‘ S j > t | = MIn+1

V j =1         J A Sj>t j=1 j

N+1

= mH l >z = П ML >t = ii . j > t 11     . j > t j =1

N+1

=П P(Sj> t) = П j (t), j=1

Подставив (7)-(9) в (6), получим

Pа (t) = 1 -

N

П

1 -

х

^F„„ (y)^dF,, (y) +

+MFY,, tV.)^0,^F,„t y ) ^dFY„t y )

^ N+1 j      t                      /

П (1 -Io FP2, (y¹dFY,, (y))

V j=1 ^x                                    .

х

х

где Pj_S (t) - вероятность того, что j-й порт концентратора не перейдет в состояние аварии к моменту времени t.

Pj_S (t) можно записать следующим образом:

PjS⁽t) =^{1 -}P⁽Р2j^At< Y2j< t)-

Проведя ряд аналитических преобразований, получим:

PS (t) = 1 - (P(Y2j< t) - P(Y2j< P2j A t)) =

= ¹- IP₂j<t^(P(Y2j< t) ^{- P(}Y2j< P2j )).

Вероятность того, что сервер не перешел в состояние аварии на интервале [0, t]:

^Pac⁽t) = ^{1 - P(}P3 ^At <^5a,3< t)-

Преобразуем это выражение:

Pac (t) = 1 - (P(5 A Y3 < t) - P(5 A Y3 < P3 A t)) = = ^{1 -}Ip₃<t^(P(5aY3< t)^-P(5aY3

3^)).

Тогда вероятность того, что на интервале [0, t] произойдет авария, можно записать следующим образом:

Pa( t) = 1 - M

^РакХ t)) | P_aс (t)

V i=1 J

В силу статистической независимости отказов запишем выражение так:

Pa( t) = 1 -

^ N+1 _ I N _ Y _

П MPjs (t) х|П MU t) | MPaс (t). (6)

Опустив промежуточные преобразования, запишем конечные соотношения:

_         (          „      ^fp„( y) dF,, (y) +

MP„,tt) = 1 - MF, (Y,)[             ,

V ’'    ^j0+ №,„(, i )fo F,^ y) dv y)

;

^MP. < t )=¹ I?:,? y ) ^dF-y y )

х

Пусть о а (t) - интенсивность аварий. Тогда o (t) = dPa( t)/ dt a       1 - Pa( t)

.

Таким образом, были получены выражения для вычисления вероятности аварии и интенсивности аварий распределенной вычислительной системы на интервале времени [0, t].

То, что показатели надежности были получены без каких-либо предположений о числе клиентов в системе и о законах распределения наработок на отказ, позволяет говорить о точности результатов.

Анализ распределенных вычислительных систем, которые моделируются как набор сервисов, предоставляемых сервером клиентским процессам, является важной задачей. Сбор и хранение данных - дорогостоящие процедуры, поскольку часто данные стоят больше, чем распределенная вычислительная система, на которой они обрабатываются. Предлагаемые процедуры надежностного анализа распределенных вычислительных систем позволяют уже на этапе проектирования предотвратить излишнее дублирование данных (для предотвращения их потери вследствие ненадежности системы) и избежать дополнительных усилий и финансовых затрат.

Предлагаемые модели могут быть использованы в современных технологиях разработки распределенных вычислительных систем, критических по обеспечению безопасности. Рассмотренный в работе набор показателей, используемых при анализе архитектурной надежности распределенных вычислительных систем, может корректироваться, так как наиболее подходящие показатели для конкретной системы определяются в зависимости от типа системы и предметной области знаний. Более того, для различных систем могут использоваться разные показатели.

В результате можно сделать следующие выводы.

• 1.    Модель анализа распределенных вычислительных систем клиент-серверной архитектуры позволяет, в отличие от существующих моделей и методов оценки надежности, без каких-либо предположений о законах распределения случайных величин и числе эле-

• ментов в системе получить соотношения для показателей надежности распределенной вычислительной системы.

• 2.    Данная модель позволяет вместо функций распределения, выраженных в аналитическом виде, воспользоваться их статистическими эквивалентами, найденными экспериментально, что особенно полезно при расчете показателей надежности распределенных вычислительных систем.

• 3.    Надежностный анализ распределенных вычислительных систем архитектуры «клиент-сервер» может использоваться для оценки надежности систем для возможных архитектурных изменений и выбора надежной архитектуры из набора вариантов, так как в зависимости от количества и величины компонентов условные и безусловные вероятности сбоя, доступа, анализа и времени восстановления, а также и времени использования компонентов различны.