Модель бесконтактного транспортного средства как системы с особой точкой

Системы бесконтактного подвешивания динамических объектов находят все большее применение в современных высокотехнологичных продуктах производства — от микромеханических гироскопов до высокоскоростных транспортных средств (ТС). Математические модели таких систем являются нелинейными, что затрудняет применение аналитических методов для решения задач анализа и синтеза при разработке новых конструктивных решений.

ПОСТАНОВКА ЗАДАЧИ

Функционально-структурные схемы электромагнитного и электростатического бесконтактных подвесов представлены на рис. 1. На нем обозначены: ЭМ — электромагнит; I — электрический ток; ВТ – взвешенное тело; U ₁ и U ₂ — электрические потенциалы, подаваемые на пластину П конденсатора и на ВТ соответственно; A U — разность потенциалов; ( x 0 - x ) — зазор между ЭМ (П) и ВТ.

В работе рассматривается возможный метод приведения нелинейной математической модели бесконтактного подвеса к интегрируемому виду линейной нестационарной модели с особой точкой.

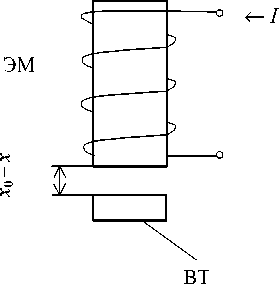
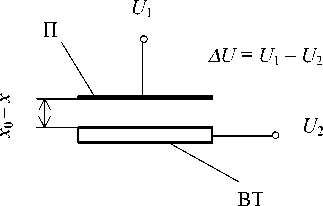
Рис. 1. Схемы бесконтактных подвесов: а — электромагнитный подвес; б — электростатический подвес. Пояснения в тексте

РЕШЕНИЕ ЗАДАЧИ

Известно, что для одностепенных электромагнитных и электростатических бесконтактных подвесов транспортных средств сила взаимодействия взвешенного тела (ротора) и статора определяется соотношениями [1]

Для построения модели, которая поддается аналитическому решению, линеаризуем входящее в формулу (3) обобщенное управляющее воздействие q в окрестности его равновесного значения q ₀

q ² ≈ q ₀ ² + k_q ⋅ q ,                     (4)

µ ⋅ µ 0 w ² S m I ² 8( x ₀ - x )² 2 ε ⋅ ε ₀ S_c ∆ U ²

( x ₀ - x )^{2    ,}

а степенную функцию f ₁ ( x ) аппроксимируем дробно-линейной функцией

f 2 =

1_. x ₀( x ₀ - k_x ⋅ x )

где µ , µ ₀ — относительная и абсолютная магнитные проницаемости соответственно; ε , ε ₀ — относительная и абсолютная диэлектрические проницаемости соответственно; S_m , S_c — площадь полюса электромагнита и эквивалентной обкладки конденсатора соответственно; I — сила тока в обмотке электромагнита; ∆ U — разность потенциалов на взвешенном теле и на статоре; x - x ₀ — величина зазора между взвешенным телом и электромагнитом (обкладкой конденсатора); x — координата взвешенного тела в текущий момент времени; x ₀ — номинальная величина зазора.

Обобщая формулы (1) и (2), представим зависимость силы бесконтактного (электромагнитного или электростатического) взаимодействия взвешенного тела с силовым полем в виде

F = ^{a ⋅ q 2} ₂ = a ⋅ f 1 ( x ) ⋅ q ²,                  (3)

( x ₀ - x )²

где a — постоянный коэффициент, зависящий от конструкции бесконтактного      подвеса;

f ₁ ( x ) =        ₂ ; q — обобщенное управляющее

( x ₀ - x )²

воздействие (сила тока или разность потенциалов).

Для эффективного исследования систем управления необходимо получить аналитическое решение для системы уравнений, включающих нелинейную зависимость (3) силы F от координат x и q . В реальных системах бесконтактного подвеса обобщенная координата может зависеть от многих переменных величин, каждая из которых описывается своим многомерным дифференциальным уравнением. В этих случаях единственным методом сведения исходной нелинейной модели к интегрируемому виду является линеаризация. Одним из известных методов линеаризации нелинейных моделей является замена аргумента нелинейной функции известной функцией времени и последующее определение коэффициентов линеаризации. Такой метод применяется, например, при гармонической линеаризации нелинейных зависимостей.

Коэффициенты линеаризации k_q и k_x подлежат определению после нахождения аналитического решения. Начальные значения коэффициентов линеаризации могут быть определены на этапе предварительной аппроксимации нелинейностей.

В качестве первого приближения к значению коэффициента kq можно принять коэффициент разложения нелинейности q2 в ряд Тейлора в окрестности равновесного значения kq = 2 ⋅ q0 .

В качестве первого приближения к значению коэффициента kx можно принять значение kx=1.38, обеспечивающее удовлетворительную аппроксимацию нелинейной функции f1 на интервале возможных значений аргумента (рис. 2).

Графики степенной функций f ₁ и дробнолинейной функции f ₂ при k_x = 1.38 приведены на рис. 2, где аппроксимируемая функция f ₁ представлена пунктирной линией, а аппроксимирующая функция f ₂ — сплошной линией.

Из рис. 2 следует, что аппроксимирующая дробно-линейная функция f ₂ на большей части области возможных значений аргумента отличается от аппроксимируемой степенной функции f ₁ не более чем на 20 %.

Предельные значения коэффициента k_x , входящего в функцию f ₂ , могут быть определены с одной стороны как значение производной от знаменателя функции f ₁ в начальной точке

k

x max

d 2

-    ( x ₀ - x )

dx x=0

= 2 ⋅ x ₀,

а с другой стороны — как коэффициент, определяющий угол наклона прямой, соединяющей точки

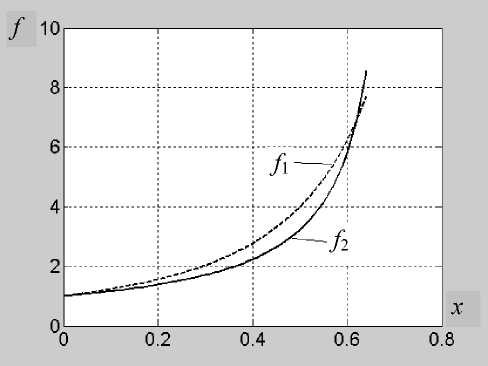
Рис. 2. Дробно-линейная аппроксимация степенной функции

параметра k_{F 0} , k_{F 1} и t ₀ , зависящих от трех неопределенных коэффициентов q ₀, ( k_x ■ v ) и k_q. Конкретные типы моделей такого вида используются при моделировании переходных процессов в акселерометрах и гироскопах с магнитным [1] и электростатическим подвесами [2], в двигателях для высокоскоростных транспортных средств на магнитной подвеске.

В общем случае линеаризованная модель бесконтактного подвеса транспортного средства с учетом нестационарности силового поля и (8) может быть представлена в виде [1]:

^^1 = x 2 + f i ,

,x 2 = а 21 x i + а 22 x 2 + а 23 - — + f 2 ,         (9)

t - t 0

x₃ = a ₃₁ x 1 + a ₃₂ x ₂ + а ₃₃ x 3 + f 3 ,

максимума и минимума функции  ( x 0 - x)²

на интервале [0, х 0 ]

^k x min

= x о .

С учетом аппроксимаций (4) и (5) модель преобразуется к виду

F =

a x о( x о - kx • x)

• ⁽ q 2 + k q • q ).

Модель (6) содержит произведение линейной функции от q на величину, обратно пропорциональную (x0 –kxx). При линеаризации нелинейной модели (6) предположим, что координата х линейно зависит от времени x = V • t, (7)

где f ₁ , f ₂ , f ₃ — возмущающие воздействия, в том числе зависящие от начальных условий; x ₁, x ₂, x ₃ — координаты вектора состояния системы, приведенные к нулевым начальным условиям; x ₁ — координата линейного смещения взвешенного тела; x 2 = x 1 — скорость линейного смещения; x ₃ = q = I — отклонение от равновесного значения силы тока в электромагнитной катушке.

Третье уравнение системы (9) составлено в предположении, что управляющее воздействие является взвешенной суммой всех трех обобщенных координат.

Структурная схема нестационарной модели бесконтактного ТС приведена на рис. 3.

где v — параметр, подлежащий определению из условия оптимальной аппроксимации переходных процессов.

С учетом аппроксимации (7) модель (6) приобретает вид, допускающий получение интегрального представления решения задачи Коши

a • ⁽ q о ² + k q q )

F =-- x0(kx • v • t - x0)

^k + k F ¹^^ , ⁽ t - t 0 ) ⁽ t - t 0 )

, a • q                     a • kq где    kF 0 = -  --------; kF! = —--------;   t 0 = kx • v • x0               kx • v • x0

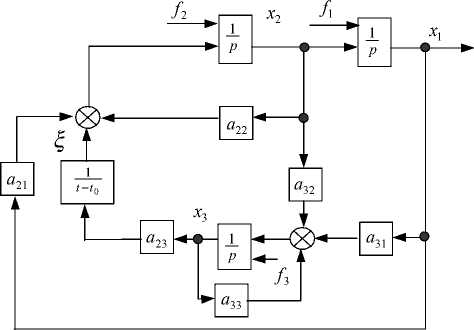
Рис. 3. Структурная схема нестационарной модели бесконтактного транспортного средства

x ₀

.

k_T • v

x

Модель (8) позволяет учесть нестационарность силового поля и включает три неопределенных

В такой постановке для решения системы уравнений (9) может быть использован метод, аналогичный методу решения обыкновенного дифференциального уравнения Лапласа с особой точкой [3].

Преобразуем второе уравнение, умножив его на т = t - t ₀ и заменив координату х ₂ в соответствии с первым уравнением системы (9):

X = X 2 + f„ т • (Xi - a21Xi - a22 .Vi) = a 23Xз + т • (f2 - a 22 f1), (10)

^X 3 = a 31 ^X 1 + a 32 ^X i + a 33 ^X 3 + f 3 ^- a 32 f 1 .

Предположим, что требуется найти решение систем уравнений (9) и (10) при нулевых начальных условиях, т. е. эти системы уравнений составлены в отклонениях от равновесного положения. Тогда решение системы уравнений (10) будем искать в виде интеграла обращения Римана—Мел-лина—Бромвича

₁ c + i ^

X(t) = — JeptX(p)dp , 2ni J c - i^

где X ( p ) = [ x 1 ( p ),..., x n ( p )]^T — преобразование Лапласа вектор-функции X ( t ) = [ x 1 ( t ),..., x n ( t )]^T состояния системы (10).

Относительно изображений получаем систему нестационарных алгебраических уравнений с двумя независимыми переменными т и р

^Т • ^[ p ^{2 -} a 21 ^- p • a 22 ^{] X} 1 ⁽ p ) =

= a 23 ^X 3 ⁽ p ) ^{+ T} • ^[ f 2 ⁽ p ) ^- a 22 f I ⁽ p ^)]; p^X 3 ⁽ p ) = ^[ a 31 ⁺ p • a 32 ^{] X} 1 ⁽ p ) ⁺

⁺ a 33 ^X 3 ⁽ p ) ^{+ f} 3 ⁽ p ) ^- a 32 f 1 ⁽ p ).

Интегрированием по частям можно показать, что имеет место соотношение

₁ c + i ^                           ₁ c + i ^        j

— f t • e p f ⁽ p ^)d p = - — J e^p‘—f ⁽ p ^)d p ,

2ni J                 2m J     dp c - i^                             c - i^

откуда следует:

c + i ^

2^4" J epf ⁽ p ^)d p = c - i ^

₁ c + i ^                                 ₁ c + i ^

= — f t • e p ^{f (} p ^)d p ^- 1 0 • — ee^ptf ⁽ p ^)d p =

2ni J                     2ni J c - i ^                               c - i^

. c+i^\

= - — J e pt — + 1 0 f ( p )d p .

2m Jd c - i ^ \/

Следовательно, дифференциальное уравнение относительно координаты X 1 может быть представлено в виде

Г d

⁺ t 0

( ^d p

• [ p p

^- a 21 ^- p • a 22 ^{] X} 1 ⁽ p ) =

= a 23 ^X 3 ⁽ p ) ^{+ T} • ^{[ f} 2 ⁽ p ) ^- a 22 ^f 1 ⁽ p ^)],

( p • a ₃₂ + a ₃,)

X 3(p) =--------------X1 (p) + p - a 33

^{+ 1}----^{[ f} 3 ⁽ p ) ^- a 32 ^f 1 ⁽ p ^)].

p ^- a 33

Приводя это уравнение к нормальной форме Коши, получим d / X

—^X 1 ⁽ p ) = d p

^- t 0

a 23 • ⁽ p • a 32 ⁺ a 31 ) ^{+ (2} p ^- a 22 ⁾⁽ p ^- a 33 ) ( p - a 33 ) • ( p ² - a 21 - p • a 22 )

^X 1 ⁽ p ) ^-

a 23 ^{[ f} 3 ⁽ p ) ^- a 32 ^f 1 ⁽ p ^{)] + т} • ^{[ f} 2 ⁽ p ) ^- a 22 ^f 1 ⁽ p ^)]( p ^- a 33 ) ( p - a 33 ) • ( p ² - a 21 - p • a 22 )

Представим это уравнение в более компактной форме d / 4

—X1(p) = dp

•

= - [ 1 0 + ^ф 1 ( p ) + Q T p )] • X 1 ( p ) - F^ ( p ),      (11)

Q ⁽ p )               ¹

_ , , a ₂₃ • ( p • a ₃₂ + a ₃1)

где Ф 1 ( p ) =------ ^{23      32} ---³¹²----- — пе-

⁽ p ^- a 33 ) • ⁽ p ^- a 21 ^- p • a 22 )

редаточная функция стационарной части системы от выхода нестационарного звена с координатой ^ до входа этого звена; Q(p) = (p2 - a21 - p • a22) — характеристический полином подсистемы с коор- динатами x1, x2 с исключенной нестационарной обратной связью;

F ⁽ Р ) =

=      a 23 ^[ f 3 ⁽ Р ) ^- a 32 f l ( Р ^)]      +

• ⁽ Р ^- a 33 ) • ⁽ Р ^{2 -} a 21 ^- Р • a 22 )

+ + ^Т • ^[ f 2 ⁽ Р ) ^- a 22 f l ( Р ^)]( Р ^- a 33 ) _

• ⁽ Р ^- a 33 ) • ⁽ Р ^{2 -} a 21 ^- Р • a 22 )

взвешенная сумма внешних воздействий, приведенная к входу нестационарного звена.

Общим решением соответствующего (11) однородного дифференциального уравнения

Оригиналом изображения (13) будет интеграл обращения Римана—Меллина—Бромвича

• ^x 1 ⁽ t ) =

• 1      Г С +

= -- X f

2га     J

V

p

c - i ^

e^{p (} t ^- t ^{0 )} ф ( p )—1- X Q ⁽ Р )

X J e zt ^{0 Ф} 1 ^{( z} ) • ф - ^{( z} ) ^{Q ( z} ) F ^{( z)dz} d Р .

ОО

/

-d x ⁽ p ) = ^- d p

* о +Ф 1 ( Р ) +

S C p ) ^{Q (} Р )

будет экспоненциальная функция

-J[ * о+Ф1( -)+Ц ] dz x 10 ( Р) = e Р 0

= e^{Р - Р} о )* о ф ( p ) Q^ l, Q ( Р )

• ^x 1 ⁽ Р )

-J Ф1( z )dz где ф(p) = e Р0     — решение дифференциаль

ного уравнения — ф(p ) = -Ф 1 ( p ) • ф (p ). d p

Общее решение неоднородного обыкновенного линейного дифференциального уравнения первого порядка (11) с переменным коэффициентом равно сумме реакций системы на начальное условие и на возмущение, так что при нулевом начальном условии общее решение совпадает с частным решением — с реакцией системы на возмущение и имеет вид [2]:

Интегральное представление вида (14) неудобно для практического использования, поскольку изображение внешнего воздействия F _S 1 ( z ) входит под знак внутреннего интеграла, что затрудняет выделение сомножителя, аналогичного параметрической передаточной функции линейных нестационарных систем общего вида [4]. Поэтому проинтегрируем (14) по частям, учитывая, что при нижнем и верхнем пределах внешнего интегрирования подынтегральные функции обращаются в нуль, т. к. модуль экспоненциальных множителей при чисто мнимом аргументе равен единице, а все передаточные функции, входящие под знак интегрирования, стремятся к нулю при увеличении модуля аргумента и, кроме того, предполагается, что подынтегральная функция во внутреннем интеграле стремится к нулю не медленнее, чем 1 p ² . При интегрировании по частям обозначим

d U = e^{p (} t ^- t ^{0 )} ф ( p )-1-d p , Q ⁽ Р )

V = J e^{zt 0} Ф 1 ( z ) • ф -* ( z ) Q ( z ) F^_x( z )d z ,

^

тогда

^x 1 ⁽ Р ) =

p

U = J e^{z (} t ^- t ^{0 )}

^

----ф ( z )d z Q ( z )

- e" ^{pt 0} ф ( p )—1- J e^{zt 0} ф "¹( z ) Q ( z ) F ^ ( z )d z . ^{(13) Q ( p} ) Р 0                    '

d V = ep* ^{0 ф} 1 ⁽ p ) • ф -^{1 (} p ) Q ⁽ p ) F ^ ₁ ⁽ p ^)d p .

Пределы интегрирования должны быть выбраны таким образом, чтобы при p ^ ^ решение неоднородного уравнения (11) стремилось к нулю, т. к. при постановке задачи предполагалось, что система (9) удовлетворяет нулевым начальным условиям, в частности, должно выполняться условие

В соответствии с общей формулой интегрирования по частям при условии, что

^{U (} Р ) • V ⁽ Р )| Р =+ ’ “ = ⁰ , получим

lim px 1 ( p ) = 0 .

Р ^^

Следовательно, в формуле (13) необходимо положить p ₀ = ~ .

.. c + i ^

x 1 ⁽ * ) = - 2 n i J d U ⁽ Р ) ^ V ⁽ Р ^)d Р = c - i ^

= ^- 1- ^{U (} Р ) • V ⁽ Р )

2 n i

p =+ i ^

p =- i ^

+

₁ c + i то

⁺ 2 П J U ⁽ Р ) ’ d V ⁽ Р ^)d P = c - i to

=--X

2 n i

^ c + i to

J e^{Pt 0} F ( p ) Q ( p ) ^ф 1 ( p ) ^X

^ c - i to

параметрическая передаточная функция системы по первой координате.

Таким образом, решение задачи Коши сведено к вычислению интегралов (15), (16), (17). В случае если начальные условия не равны нулю, в исходной системе уравнений (9) необходимо сделать обычную замену переменных [5]:

p

X Ф "*( P ) J e^z

TO

ОЙ

Ф ( z )d z d p

J

где т = t - t ₀.

Таким образом, искомое решение по первой координате может быть представлено в виде

1                       1 m_x ,m_;

x j = x j о ^{+ x} j0 • t + •" +---- x j 0 j • ^t j + У],    ⁽¹⁸⁾

m j -!

(j = 1, 2, 3),

x i ^{( t} ) =

c + i то

1 c ⁺ i

= у J № ( P ) •

2m Л 1

e"^{p T} Q ( P ) Ф 1 ( P ) X

c - i to

p

X ф ⁴( p ) J e^{z T}

TO

----ф ( z )d z

Q ( z )

■ d p .

Выражение, стоящее в квадратных скобках формулы (15), представляет собой параметрическую передаточную функцию линеаризованной нестационарной системы управления бесконтактным транспортным средством по воздействию с изображением F^ ( p ).

Решение по остальным координатам в изображениях может быть получено из первого и третьего уравнений системы (10) после применения пре-образованияЛапласа:

где x j ₀, x ]-₀, — x ™0 — начальные условия по j -й координате и ее производным до m j -го порядка включительно.

После замены переменных (18) решение системы (9) сводится к решению этой же системы, но относительно новых переменных у₅ с нулевыми начальными условиями и с измененными правыми частями.

В случае, когда для электромагнитной подвески используется несколько электромагнитов, система уравнений (9) преобразуется к виду

^^1 = x 2 + f , ;

x ₂ = a ₂₁ x 1 + a ₂₂ x ₂

x ₃ = a ₃₁ x 1 + a ₃₂ x ₂

1                       -

+ ——^ a 2 j x j ⁺ f 2 ;

^{t 1} 0 j = 3

n

+ ^ a 3 j x j + f ₃;

j = 3

x 2 ^{( t} ) =

- c + i то

= — J e ^ ^[- f l ( P ) ⁺ PF ⁽ P^{)T (} P , ^{T ) ] d} P ,     (16)

2m J                   1

c - i to

x

n

n

- a a +> a -x - + f .

n 11      n 2 2    / > nj / Jn , j=3

-     c+i to          „ x3(t)  2 .X J ept —-—dp,

2ni          p - алл c - ito       r 33

где

⁵ = f 3 ⁽ P ) ^- a 32 f l ( P ) ^{+ (} a 31 ⁺ a 32 P ) ^Fz_x ⁽ P ) ^{T (} P , ^т );

T ( P , т ) =

p 1

= e" ^{p T} Q ( p ) Ф 1 ( p ) • ф -¹ ( p )J e^{z T} — ф ( z )d z - TO     ^{Q ( z} )

где x j (j' = 3, 4,^, n ) — обобщенные управляющие воздействия, соответствующие j -му электромагниту; ay ( i = 2,^, n; j = 1, 2,^, n ) — постоянные коэффициенты, n - 2 — количество электромагнитов.

В отличие от модели (9) модель (19) содержит ( n - 2) переменных коэффициентов. Покажем, что модель (19) приводима к системе с переменным коэффициентом лишь при одной переменной x 1 .

Умножим второе уравнение системы (19) на ( t - 1 ₀). Тогда система (19) преобразуется в систему с одним линейно изменяющимся коэффициентом при одной координате вектора состояния

( t - t o )( x - a 21 x 1 - a 22 x j = n

= ^ a 2 j x + ⁽ t - t 0 ^{)( f} 2 - a 22 ^f I );

j = 3

n x 3 = a 31 x 1 +2 a 3 jxj + f3;                 (20)

j = 3

n x = a + У a x + f . n       n1 1             nj j n .

j = 3

В системе уравнений (20) переменный коэффициент содержится лишь в первом уравнении при одной переменной x ₁ и ее производных, что позволяет решить задачу аналогично рассмотренной выше модели с одномерным бесконтактным подвесом.

ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ

Движение транспортного средства в вертикальной плоскости в общем случае происходит под действием управляющего воздействия, демпфирующих и гравитационных сил. Состояние статического равновесия в бесконтактных подвесах в соответствии с теоремой Ирншоу является неустойчивым, поэтому система подвешивания работает в режиме установившихся колебаний с достаточно малой амплитудой.

Работа системы происходит следующим образом. Управляющее воздействие q приводит ВТ в движение во взвешенном состоянии. В момент времени t = t *, соответствующий достижению ко *

ординатой x ₁ заданного значения x ₁ , параметры управляющего воздействия q ₀ и k_q изменяются так, что система начинает движение в обратном направлении. После достижения первой координатой значения x ₁ = x ₀ восстанавливаются параметры управляющего воздействия, соответствующие движению ВТ в прямом направлении, и цикл повторяется. Вертикальное движение бесконтактного транспортного средства как в прямом, так и в обратном направлениях моделируется системой уравнений (20).

ЗАКЛЮЧЕНИЕ

Предложенная в работе модель бесконтактного подвеса может быть отнесена к классу моделей линейных нестационарных систем управления с особой точкой. Модель может быть использована для анализа и синтеза недифференциальных схем систем управления гироскопами и бесконтактными транспортными средствами.