Модель численного роста народонаселения Китая в ХХ-XXI вв.

Исходные положения

Демографическая динамика, вызывающая значительный научный и практический интерес, с позиций ее математического моделирования может быть представлена различным образом, поскольку каждая из моделей презентирует какой-либо аспект реального процесса и поскольку ни одна модель не может охватить все стороны и всю глубину социальной действительности. В плане наиболее общих концепций демографического роста на настоящий момент выделяются гиперболическая модель [1, т. 166, c. 63–79], по которой количественное увеличение населения достигает некоторого уровня, обусловливающего фазовый переход и дальнейшую стабилизацию процесса на предельно допустимом значении, и традиционная модель геометрической прогрессии. Последняя имеет не только устойчивую традицию, но и основана на довольно строгой логике. Так, если численность населения на начало года (не имеет принципиального значения - региона, страны или всего мира) равна S 0 , и за год измерения произошло n рождений и m смертей, то на начало следующего года численность населения составит: s, = s₀ + n - m .

Несложные преобразования приводят к следующему уравнению:

S = So [ 1 + ;n - m 1 = So ( 1 + kn - km ) = So(1 + k),

V    ^So   ^So )

где k n = n/S 0 - коэффициент рождаемости года измерения;

k m = m/S 0 - коэффициент смертности того же периода;

k = k n - k m - коэффициент прироста населения в год измерения.

В свое время Эйлером было доказано существование предела подобного уравнения _lim [ 1 ₊ 1 Y = e в z ^” V    z )

виде иррационального числа е = 2.71828... Подставляя k вместо 1/z, получаем: (1 + k)^1k = V1 + k = e . И возводя обе части уравнения в степень k, окончательно имеем 1 + k = e^k . Иначе говоря, рост численности населения представлен экспоненциальной функцией так, что S, = S_oe^kt , где t - любой по продолжительности период времени.

Представим N как абсолютное число всех рождений и M как абсолютное число всех смертей, сколько бы их ни было на самом деле. Тогда очевидно, на любой момент времени t 0 их разность равна численности живущих S: n₀ - м₀ = s₀ .

А на следующий момент времени t i : N - Mj = Sj.

Допуская в качестве математической идеализации постоянство коэффициента прироста k, получаем на любой момент времени

N 1 - M i = S o e kt ;    (N o - M o ) e kt = S o e kt ;   N o e kt - M o e kt = S o e kt .

Поскольку разность абсолютного числа всех рождений и абсолютного числа всех смертей равна количеству живущих на текущий момент времени, то функция абсолютного числа всех смертей f (M) в момент t 1 через время продолжительности жизни погодовых поколений T необходимо повторяет функцию абсолютного числа всех рождений f (N) в момент t 0 . В силу этого обстоятельства возрастание ее значений происходит с той же скоростью, что и функции f (N) с некоторым запаздыванием, но с тем же коэффициентом прироста. А коль скоро так, то этот коэффициент прироста и есть коэффициент прироста численности населения k.

Иначе говоря, скорость изменения функций абсолютного числа всех рождений и абсолютного числа всех смертей теоретически одинакова со скоростью прироста численности населения на ее экспоненциальном этапе при условии постоянства коэффициента прироста. Несмотря на некоторую абстрактность понятий абсолютного числа всех рождений и абсолютного числа всех смертей, как будет ясно из дальнейшего изложения, они имеют важное, если не принципиальное, значение.

В русле мальтузианской концепции лежит представление о популяционной динамике Ферхюльста, которое широко и удачно используется в современной экологии. Суть идеи состоит в том, что любая популяция имеет предел своей численности, обусловленный «несущей способностью» территории ее обитания или, иначе, объемом ее экологической ниши. Вследствие этого коэффициент прироста k оказывается зависимым от свободного остатка экологической ниши и постоянно уменьшается при приближении численности популяции к максимуму, будучи связанным коэффициентом пропорциональности R, который имеет некоторое константное значение и носит название параметра роста [2, c. 39]:

к

---------= R;

' °maxLJ

В результате экспоненциальная функция изгибается, приобретая характер логистической кривой.

По отношению к социуму формулу Ферхюльста можно переписать в виде k = R (1 - P), где Р = S/S max (S - численность народонаселения на текущий момент времени, S max - объем экологической ниши общества, то есть максимально возможная численность населения или несущая способность территории, P - демографическое давление). Но по отношению к социуму нельзя говорить, что его экологическая ниша жестко определена, ибо своим трудом и интеллектом человечество постоянно раздвигает ее границы, расширяя и углубляя ее пространство. Подтверждением этому выступает сохранение коэффициентом прироста на протяжении длительного времени практически постоянного, устойчивого значения. Например, по ревизским сказкам XVIII–XIX вв. численность народонаселения России возрастала в среднем с годовым коэффициентом 0.01224, или 12,24 ⁰ / 0 [3, c. 216].

Подобные ситуации показывают, что не только численный рост населения носит экспоненциальный характер - S 1 = S 0 e ^k , но и процесс расширения экологической ниши имеет те же параметры - ^q . Если k = q, скорость прироста остается неизменной. Усилия общества по расширению эко- max₁      max ₀

логической ниши в текущем году, определяют коэффициент прироста населения на следующий год, по- этому ko j k1 = RI1 -

^S o ^e       I

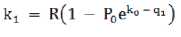
S      eq' I o ^,или

Будем считать доказанным для человеческих популяций равенство параметра роста константному значению lnC2 = 1,561552813… [4, т. 2, c. 716–725]. Тогда величина демографического давления на любой момент времени определена как lnC2 — к к = 1пС2 ■ (1 - P); к = lnC2 — lnC2 ■ P; P inC2 "

Однако сразу же следует заметить, что логистический характер имеет не собственно функция численного роста популяции f (S). На примере демографической статистики Китая, сведения о которой сохранились с глубокой древности, мы можем видеть, как уже несколько раз количественное увеличение его населения упиралось в стенки экологической ниши, иногда с катастрофическим снижением численности народонаселения [5, c. 147]. Поэтому в общецивилизационном плане следует считать, что логистическим характером обладает функция численного роста абсолютного количества всех смертей f (M). Во-первых, потому что ни функция абсолютного числа всех рождений f (N), ни функция абсолютного числа всех смертей f (M) не могут иметь отрицательного коэффициента прироста. Во-вторых, потому что человечеству свойственно вообще, а в условиях современности в особенности, представление о ценности индивидуальной жизни. И все усилия человечества в отношении углубления своей экологической ниши направлены на создание условий, позволяющих увеличить срок существования индивида, а следовательно, снизить смертность, в первую очередь, детскую. Но это снижение осуществляется при запаздывающем (в силу инертности репродуктивных традиций) падении рождаемости. В результате и функция абсолютного числа всех рождений f (N) также становится логистической.

Еще в 1929 г. Л. Рабинович, правда, на позициях теории К. Маркса, предложил рассматривать демографическую эволюцию в соответствии с изменением способов производства. На первой стадии – до промышленной революции – высокая рождаемость и высокая смертность при крайне низком коэффициенте прироста. За промышленной революцией происходит и демографическая революция, которая проявляется в снижении смертности и изменении репродуктивных установок населения в сторону снижения рождаемости [6, c. 187–188].

Следует, однако, в общетеоретическом плане вести речь о стадиях развития общества и соответствующих им демографических процессах. Стадии собирательского и охотничьего общества – присваивающего хозяйства – характеризуются очень медленным увеличением численности населения ввиду высоких значений коэффициентов рождаемости k n = n/S и смертности k m = m/S. При этом функции f (N), f (M) и f (S) носят экспоненциальный характер, но с крайне низким коэффициентом прироста k. С переходом к аграрно-пасторальной стадии рождаемость остается столь же высокой, но смертность уменьшается по причине улучшения и большей стабильности условий жизнеобеспечения. Численность населения начинает быстро расти, а само население распространяться на все возможные для аграрного и пасторального хозяйства территории, сталкиваясь с другими народами, ведя перманентные захватнические и/или оборонительные войны, которые, как и эпидемии, выступают фактором, сдерживающим демографический рост. Бум рождаемости, демографическая революция приходятся на ту стадию общества, когда оно становится аграрно-индустриальным и подвергается урбанизации при распространении и соблюдении норм гигиены и санитарии. Успехи медицины индустриальной стадии развития обеспечивают сохранение жизни подавляющей части новорожденных, что при сохраняющихся репродуктивных традициях аграрного общества и создает условия для демографической революции. Запаздывающее изменение репродуктивных традиций приводит к достижению максимума численности населения, которое затем начинает сокращаться. Переход к постиндустриальной стадии социального развития характеризуется и низким коэффициентом смертности, и низким коэффициентом рождаемости. Это – конец истории, точнее – конец социальной истории. Стабилизация демографического процесса и депопуляция означает в то же время стабилизацию социальных структур при безудержном информационно-научном прогрессе. Сохранение латентной экспоненциальной тенденции численного роста населения консервирует возможность демографического ренессанса, но если изменятся условия. Скажем, выход человечества на просторы Вселенной и превращение его во Вселенское человечество может быть тем фактором, который возродит экспоненциальный рост его численности.

Определение временной точки максимума численности населения

Положение о демографическом давлении как величине, производной от человеческих усилий, позволяет на этапе демографической динамики, на котором проявляется тенденция уменьшения численности населения, прогнозировать время достижения максимума функции f (S) при условии, что эта тенденция сохраняется. Условие это достаточно жесткое, поскольку связано с изменением репродуктивных традиций и становлением новой традиционности воспроизводства населения, трансформировать которую уже значительно труднее. Если снижение рождаемости является естественной реакцией на снижение смертности, когда малое число детей в семье вполне удовлетворяет потребность в реализации родительских чувств и в передаче социального капитала, то обратное движение к увеличению рождаемости – проблема в условиях индустриального, переходного, а тем более постиндустриального общества – практически неразрешимая. Поэтому можно считать, что с проявлением и установлением тенденции она уже остается весьма устойчивой и измеримой.

Например, по Российской Федерации на начало 1960 г.: k = 0,0158; Р = 0,9645. На начало 1980 г., то есть за 1979 г.: k = 0,0049; Р = 0, 989. 1960 г. взят в качестве точки отсчета по той причине, что именно в этот год численность городского и сельского населения в России сравнялась. Приток сельского населения в город активно продолжался на всем протяжении 60-х гг. Параллельно воспроизводству сельских репродуктивных традиций в городе и общему снижению смертности при значительном росте качества медицинского обслуживания произошло превышение нормы, обеспечивающей расширенное воспроизводство социальной структуры в стационарном режиме, отношения коэффициента рождаемости и смертности (k n /k m = 1,56), которое даже превысило значение «2». Но с конца 60-х тенденция к снижению рождаемости становится устойчивой, и пропорция устремляется к «1». Чтобы изменить направление движения к максимуму демографического давления требовался мощный технологический прорыв и трансформация социальной организации, хотя и это вряд ли могло решительно изменить тенденцию ввиду ее общецивилизационного характера. За приведенные 20 лет значение k – q в среднем составило:

к - q = ^rln(lnC2 - 0,0049)

-------—-------------- = 0,001254855...

1пС2 - 0,0158

Таким образом, при сохранении данного темпа достижение максимума численности населения должно было произойти через время

001254855 In 1

то есть в Российской Федерации, цементировавшей все объединение республик в Советский Союз, максимум демографического давления при сохранении тенденции был бы достигнут в 1988–1989 гг. Однако сказалось то, что многочисленное поколение 60-х вступило в брачный возраст, и накатившая демографическая волна отодвинула достижение максимума численности населения к 1993 г. С 1994 г. коэффициент прироста становится отрицательным [7, c. 241]. Возможно, приведенный прогноз оказался бы точнее при выборе других, более существенных реперных точек для измерения демографической динамики. Во всяком случае, в отношении современного Китая мы воспользуемся более тщательно подобранными временными интервалами для вычислений. Для этого приведем следующую таблицу, к которой будем еще обращаться неоднократно и по другим вопросам.

Таблица 1 - Основные данные по народонаселению Китая за 1949-2003 гг.

Год	Общее число населения на конец года (10 тыс. человек)	Коэффициент рождаемости (‰)	Коэффициент смертности (‰)	Темп естественного прироста (‰)	Суммарный коэффициент рождаемости	Отношение k n /k m
1949	54 167	36,00	20,00	16,00	6,14	1,80
1950	55 167	37,00	18,00	19,00	5,81	2,06
1951	56 300	37,80	17,80	20,00	5,70	2,12
1952	57 482	37,00	17,00	20,00	6,47	2,18
1953	58 796	37,00	14,00	23,00	6,05	2,64
1954	60 266	37,97	13,18	24,79	6,28	2,88
1955	61 465	32,60	12,28	20,32	6,26	2,65
1956	62 828	31,90	11,40	20,50	5,85	2,80
1957	64 653	34,03	10,80	23,23	6,41	3,15
1958	65 994	29,22	11,98	17,24	5,68	2,44
1959	67 207	24,78	14,59	10,19	4,30	1,70
1960	66 207	20,86	25,43	–4,57	4,02	0,82
1961	65 859	18,02	14,24	3,78	3,29	1,27
1962	67 295	37,01	10,02	26,99	6,02	3,69
1963	69 172	43,37	10,04	33,33	7,50	4,32
1964	70 499	39,14	11,50	27,64	6,18	3,40
1965	72 538	37,88	9,50	28,38	6,08	3,99
1966	74 542	35,05	8,83	26,22	6,26	3,97
1967	76 368	33,96	8,43	25,53	5,31	4,03
1968	78 534	35,59	8,21	27,38	6,45	4,33
1969	80 671	34,11	8,03	26,08	5,72	4,25
1970	82 992	33,43	7,60	25,83	5,81	4,40
1971	85 229	30,65	7,32	23,33	5,44	4,19
1972	87 177	29,77	7,61	22,16	4,98	3,91
1973	89 211	27,93	7,04	20,89	4,54	3,97
1974	90 859	24,82	7,34	17,48	4,17	3,38
1975	92 420	23,01	7,32	15,69	3,57	3,14
1976	93 717	19,91	7,25	12,66	3,24	2,75
1977	94 974	18,93	6,87	12,06	2,84	2,76
1978	96 259	18,25	6,25	12,00	2,72	2,92
1979	97 542	17,82	6,21	11,61	2,75	2,87
1980	98 705	18,21	6,34	11,87	2,24	2,87
1981	100 072	20,91	6,36	14,55	2,63	3,29
1982	101 654	22,28	6,60	15,68	2,87	3,38
1983	103 008	20,19	6,90	13,29	2,42	2,93
1984	104 357	19,90	6,82	13,08	2,35	2,92
1985	105 851	21,04	6,78	14,26	2,20	3,10
1986	107 507	22,43	6,86	15,57	2,42	3,27
1987	109 300	23,33	6,72	16,61	2,59	3,47
1988	111 026	22,37	6,64	15,73	2,31	3,37
1989	112 704	21,58	6,54	15,04	2,25	3,30
1990	114 333	21,06	6,67	14,39	2,17	3,16
1991	115 823	19,68	6,70	12,98	2,01	2,94
1992	117 171	18,24	6,64	11,45		2,75
1993	118 517	18,09	6,64	11,60		2,72
1994	119 850	17,70	6,49	11,21		2,73
1995	121 121	17,12	6,57	10,55		2,61
1996	122 389	16,98	6,56	10,42		2,59
1997	123 626	16,57	6,51	10,06		2,55
1998	124 761	15,64	6,50	9,14		2,41
1999	125 786	14,64	6,46	8,18		2,27
2000	126 743	14,03	6,45	7,58		2,18
2001	127 627	13,38	6,43	6,95		2,08
2002	128 453	12,86	6,41	6,45		2,00
2003	129 227	12,41	6,40	6,01		1,94

Правда, мы не можем позволить себе в полной мере доверять официальной статистике. Памятуя слова Марка Твена о том, что существуют три вида лжи – просто ложь, наглая ложь и статистика, мы поставим под сомнение величину коэффициентов рождаемости и смертности. Рождаемость и смертность, несмотря на равенство разности их коэффициентов коэффициенту прироста численности населения (k = kn – km), легко могут быть искажены для достижения политических интересов. Так, снижение смертности является показателем общего экономического роста и, прежде всего, следствием повышения культурных условий жизнедеятельности, включая сферы труда и отдыха. Поэтому можно допустить наличие естественного желания политиков видеть результат своей деятельности по управлению обществом в снижении смертности населения, которое подчеркивает преимущества наличествующего социального строя. Прово димая в Китае политика ограничения деторождения тоже должна была дать свои результаты, а решение руководства о необходимости снижения рождаемости – неукоснительно проводиться в жизнь и выполняться всем населением, что показывало бы его доверие политическому режиму и преданность господствующей идеологии. Соответственно от органов государственной статистики и их сотрудников требуется подача такой информации, которая не противоречила бы представлениям о прогрессе общества и ожиданиям политиков от результатов собственной деятельности.

Высказанное недоверие к показателям рождаемости и смертности сильно сужает возможности использования статистической информации данного исследовательского полигона. Однако думается на показатель прироста населения можно опираться в достаточной степени уверено. Коэффициент прироста насе-

ления как показатель трудно исказить, во-первых, потому, что он имеет стратегическое значение для учета трудовых ресурсов, а во-вторых, потому, что легко проверяем соотношением прироста населения и его общей численности. Поэтому в основном будем использовать показатели естественного прироста населения, однако в ряде случаев нам не обойтись без обращения к коэффициентам рождаемости и смертности, и не остается ничего другого, кроме осторожного принятия официальных данных в качестве истинных.

Судя по приведенной таблице, функция роста численности населения f (S) дважды пересекает функцию роста абсолютного числа всех смертей f (M) – в 1950 и в 2002 гг. Это те временные моменты, где коэффициент смертности равен коэффициенту прироста населения. Значение S заключено между функциями абсолютного числа всех рождений f (N) и абсолютного числа всех смертей f (M), и в то же время может рассматриваться в качестве самостоятельной функции f (S). Поэтому в месте пересечения функций f (S) и f (M) значение S совпадает со значением M, и на момент пересечения коэффициенты прироста функций f (S) и f (M) равны.

Однако само это пересечение может быть только в том случае, если возрастающая функция f(S) меняет свой экспоненциальный характер на параболический, имея точку перегиба посередине между точками пересечения в 1950 и в 2002 гг., то есть в 1976 г. Соответственно тенденция, заданная после 1976 г., будет продолжать действовать и на последующем этапе, что позволяет по изменению демографического давления в данный период предположить достижение им максимального значения через время t, после чего численность населения начинает снижаться. Характер демографического давления задан разностью коэффициента прироста численности населения k и коэффициента расширения экологической ниши q: k – q. Поэтому rZ06Z — r1976e ■

k-q = ^ln(lnC2 - к2Оог)

lnC₂ ^1976

= ^ In^lnC,

- 0,00645) ---------- = 0,000548915...

lnC2 - 0,01266

В точке максимального давления Р = 1. Поэтому вершина кривой численного роста может быть прогнозируема через время t, считая от 2002 г.,

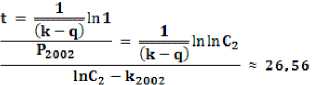
иначе говоря, не ранее рубежа 2028/2029 гг. (рис.1).

,

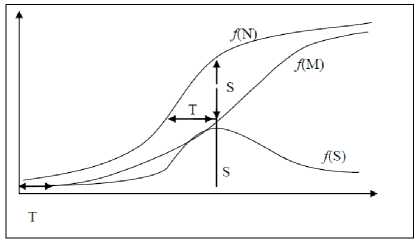
Рисунок 1 – Временная точка максимума численности населения

Сами китайские демографы, исходя из других оснований, несколько иначе оценивают момент достижения максимума численного роста населения. Результатом усилий по преодолению «бума деторождения» 60–70-х гг. ХХ в. стало снижение суммарного коэффициента рождаемости с 6 детей на каждую женщину фертильного возраста в 1970 г. до 1,7–1,8 в 2000 г. Темпы прироста населения снизились с 23 ‰ в начале 70-х гг. ХХ в. до 6 ‰ 2005 г. Таким образом, прогнозируется, что рост численности населения Китая будет продолжаться еще в течение 25 лет, но темпы естественного прироста населения будут активно снижаться. Если суммарный коэффициент рождаемости и дальше сохранится на уровне 1,7–1,8, то максимум численности будет достигнут около 2035 г. Коэффициент рождаемости станет равным коэффициенту смертности, прирост численности населения станет равным нулю. Затем численность населения будет постепенно уменьшаться, и Китай станет на путь негативного прироста [8].

Максимальная численность населения Китая

Относительно максимальной численности, к которой придет рост популяции в расчетный момент, можно сказать, что это более сложный вопрос, не столько со стороны математического аппарата, который остается довольно простым, сколько с позиций логики, позволяющей прийти к рациональным выводам.

Численный рост S, как уже говорилось, заключен между двумя функциями – абсолютного числа всех рождений f (N) и абсолютного числа всех смертей f (M) и представляет собой разность их значений на каждый текущий момент времени. При этом в результате изменения культурных условий функция f (M) меняет свой экспоненциальный характер, превращаясь в логистическую кривую, которая с этого момента имеет собственный, отличный от f (S), коэффициент прироста. Но в точках пересечения с ней коэффициент прироста функции f (S) равен коэффициенту прироста функции f (M). Иначе говоря, обозначив через m количество умерших в течение года и через k m – коэффициент смертности, имеем

^т “ S — м поскольку S = M в точке пересечения функций. В этой же временной точке, поскольку k = kn – km, коэффициент рождаемости равен удвоенному коэффициенту смертности kn = 2km. А поскольку разность абсолютного числа всех рождений и абсолютного числа всех смертей равна численности живущих на текущий момент, то в точке пересечения функций f(S) и f(M) абсолютное число всех рождений равно N = 2M = 2S.

С другой стороны, индустриализация страны и ее урбанизация приводят к тому, что рождаемость неизбежно снижается, и функция абсолютного числа всех рождений в результате тоже принимает логистический вид.

При приближении к точке перегиба коэффициенты прироста функций f (S) и f (N), прежде – на этапе экспоненциального роста сохранявшие равенство – расходятся, что требует определения собственного коэффициента прироста f (N). Это возможно благодаря наличию двух точек пересечения функций f (S) и f (M), в которых N = 2S. Можно считать с некоторой долей условности, что N max = const, хотя, конечно, это не более чем условность и идеализация, поскольку в действительности изменение потолка, верхней планки роста N находится в зависимости от усилий общества по расширению своей экологической ниши. Однако, принимая эту идеализацию при условии продолжительно действующей тенденции, а с момента индустриализации общества она становится господствующей тенденцией, связанной с переориентацией на углубление экологической ниши и соответствующего увеличения продолжительности жизни составляющих общество индивидов, получаем по уравнению логистической кривой, что

Nmax _     1 Nrnax^ _     1

N_t e^t. + 1 _и          e-^t, + i

, где N1 – абсолютное число всех рождений на момент t1 при первом пересечении функций f(S) и f(M), где M1= S1950 и N1 = 2S1950;

N 2 – абсолютное число всех рождений на момент t 2 при втором пересечении f (S) и f (M), где M 2 =

S 2002 и N 2 = 2S 2002 ;

х = const – собственный коэффициент прироста логистической функции f (N);

t 0 = 0 – точка перегиба функции f (N);

N max – условное значение максимума абсолютного числа всех рождений.

Поэтому

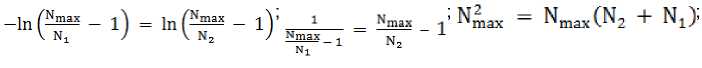
= 2 (551 670 +1 284 530) = 3 672 400 тыс.

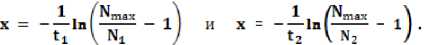
Так как          , считая от точки перегиба логистической кривой t 0 = 0, то

Откуда

X =--In - 1 = 0,03250762

, и, следовательно, абсолютное число всех рождений на 2029 г. равно .

Точно также определения собственного коэффициента прироста требует и логистическая функция абсолютного числа всех смертей f (M).

До аксиоматичности интуитивно ясно, что наибольшее по оси ординат расстояние между двумя не-пересекающимися логистическими функциями расположено на равном удалении по оси абсцисс от точек их перегиба. Логистическая функция может рассматриваться как экспоненциальная до точки перегиба и как логарифмическая после точки перегиба, таким образом, между двумя непересекающимися логистическими функциями на экспоненциальном этапе расстояние по оси ординат возрастает, а на логарифмическом этапе уменьшается. А значит, наибольшее расстояние между ними по оси ординат равно удалено от точек перегиба обеих функций по оси абсцисс. Следовательно, точка перегиба функции f(M) относится к 2082 г. Однако в этой временной точке значение функции абсолютного числа всех смертей составляет половину от ее максимума. Максимальное значение Nmax и максимальное значение Mmax – это одна и та же величина, поскольку абсолютное количество всех смертей не может быть больше, чем абсолютное количество всех рождений, а при достижении обеими функциями максимума численность S = 0. В результате получаем значение функции f(M) в точке перегиба как 0,5Mmax = 1 836 200 тыс. Но нас оно не особо интересует потому, что важнее определить значение функции f(M) на момент достижения максимального значения функции f(S), то есть на 2029 г.

В уравнении логистической кривой функции f (M)

М        1

.

Откуда

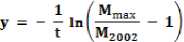
1     , /3672400

2082 - 20021П11284530

Следовательно,

0.00775011

М2029 = 4^77 = 1464 299 (тыс.чел.)

где t = 2029 – 2082 = –53 года.

В результате на 2029 год, когда функция f (S) достигнет максимума, численность населения КНР будет равна

3 116 041 – 1 464 299 = 1 651 742 (тыс. чел.).

Иначе говоря, на момент достижения максимального значения функцией численного роста f (S) количество населения КНР не будет превышать значения 1,7 млрд. человек.

Несмотря на высказанное, недоверие к точности официального статистического материала, мы постарались по возможности опираться на более или менее достоверные данные. Во всяком случае, точка перегиба функции f (S), отнесенная нами к 1976 г., визуально очевидна по изменению коэффициента прироста населения. И даже если коэффициент рождаемости дан с некоторым стабильным искажением и занижен одновременно с коэффициентом смертности, также визуально ясно, что функция абсолютного числа всех рождений имеет точку перегиба, приходящуюся тоже на 1976 г. или близко к нему. Можно практически не сомневаться в статистических показателях 1950 г., но тогда вторая точка пересечения функций f (S) и f (M) действительно приходится на 2002 г. А это дает основания для принятия приведенного прогноза в качестве достаточно убедительного.

Ссылки: