Модель циклической деградации материала в расчете долговечности составного диска

Рис. 1. Циклическая деградация стали 20ГЛ усталостной кривой) статическая диаграмма пластичной в исходном состоянии стали 20ГЛ вырождается в билинейную диаграмму, характерную для хрупкого материала. При поддержании заданной циклической деформации E M = const. и достаточно большой жесткости нагружающего устройства возможно дальнейшее циклирование при снижающемся уровне максимального напряжения цикла. Вплоть до равновесного разделения образца на две части при числе циклов N _P . Такая возможность рассматривалась в работе [3] при решении модельной задачи об усталостном разрушении составного диска при осесимметричном циклическом нагружении.

Рассматривался тонкий составной диск радиуса R 2 , ограниченный окружностью Г 2 (рис. 2). Данный конструктивный элемент изготовлен следующим образом. Внутрь кольца, ограниченного окружностями Г 1 и Г 2 , вставлен диск радиуса R 1 и по границе Г 1 осуществлено их жесткое сцепление. Диск работает в условиях пульсирующего нагружения, когда на поверхности Г 2 заданы равномерно распределенные силы q , изменяющиеся циклически в интервале 0, qM , либо перемещения и точек границы Г 2 изменяются в интервале 0, им •

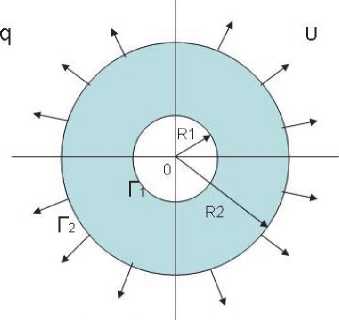
Рис. 2. Составной диск

Внутренний диск изготовлен из того же материала, что и кольцо, только прошедшего предварительную обработку, в результате которой произошло уменьшение пределов текучести и прочности, а также изменились пластические и циклические свойства. Свойства же на стадии упругости остались прежними.

Полагаем, что прочность материала кольца выше, чем у диска настолько, что он остается упругим до полного усталостного разрушения внутренней зоны. Модули упругости материалов диска и кольца одинаковы и не меняются в ходе циклирования до числа циклов N, определяемого усталостной кривой. Для упрощения расчета долговечности центральной зоны диска считаем, что напряжения в кольце не превышают предела выносливости и вырождения статических свойств материала при циклировании не происходит. Таким образом, диск радиуса R 2 представляет собой сплошное кусочно-неоднородное тело.

Исходные статические свойства материала внутреннего диска ( 0 <  r <  R 1 ) определяются полной диаграммой деформирования с падающим участком, полученной при одноосном растяжении и выраженной в интенсивностях напряжений и деформаций. Отметим также, что при n <  N на каждом полуцикле нагружения связь между напряжениями и деформациями отвечает закону Гука, т.е. для плоско-напряженного состояния, в котором находятся кольцо и внутренняя зона составного диска в условиях осесимметричного нагружения, имеем

EE

^. —2(er + ve^, °в = Е + Е (1)

Предельная поверхность разрушения материала ослабленной зоны в ходе циклического нагружения определяется формулой f (^) = ^i^ Sb (^м ,n)• (2)

В силовом подходе в качестве контролирующего параметра усталостного процесса выбирается циклический предел прочности S_B ⁽ ^ м ^,n) . В области многоцикловой усталости семейство подобных экспериментальных кривых для разных уровней напряжения ст _м аппроксимируется подходящей функцией, например, степенной

S b ( ^ м ; n) = S bo - k . n m , (3) а усталостное разрушение при п _м =const определяется равенством

SB (^N , N) = ^м , где N – число циклов по усталостной кривой.

Определив эквивалентность двух циклических состояний материала при разной истории нагружения равенством

S B ⁽ ^ м 1 , ^П 1 ) ^_ S B ⁽ ^ м 2 , n 2 ) , ⁽⁴⁾ смену напряжений можно интерпретировать как переход с одной кинетической кривой на другую и смену интенсивности накопления повреждений [3]. В этом случае нет необходимости вводить явно в расчет понятие поврежденности, а критерий усталостного разрушения обобщается на ступенчатое нагружение

^СТ МК

> S b

k

^ м ⁽ n ), Е n i

i

Если реализуется жесткое нагружение ( Е _м = const), то в каждом (из следующих за N ) цикле нагружении продолжается вырождение статической диаграммы деформирования, а именно, падает значение предела прочности. Считаем, что падение предела прочности за Д n 1 циклов происходит согласно формуле (3) и он снижается до точки А (рис. 3).

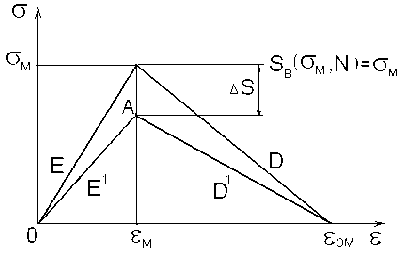
Рис. 3. Циклическая деградация ПДД при n>N

В отличие от работы [3] полагаем, что когда в полуцикле разгрузки напряжения упадут до нуля, остаточных деформаций не образуется (рис. 3). Такое поведение хрупкого материала характерно для многоцикловой усталости, когда усталостная трещина развивается без видимых остаточных деформаций. Полагаем, что отношение модуля упругости к модулю спада остается неизменным, тогда при циклическом снижении прочности на Д S B модуль упругости уменьшится на величину Д E = Д 8 B / Е _м .

Материал при стационарном нагружении E M = const остается упругим, но с новыми модулями и с новым коэффициентом поперечной деформации

E ¹ = E -A E = E -A S_R Iе_м ;

BM i E1

D¹ = DE ¹; V = V E E

в уравнениях связи напряжений и деформаций (1). Последнее выражение в (5) записано на ос- новании результатов моделирования и испытаний чугуна [5].

В задаче с диском при стационарных граничных условиях и n <  N напряженное состояние стационарно, т.е. справедлива формула (2). Но перераспределение напряжений, связанное со снижением модуля материала центральной зоны при n>N, делает ее нагружение нестационарным даже при неизменных граничных условиях. Меняется и правило перехода с одной кинетической кривой на другую, определяемое ранее равенством (4). В отсутствие экспериментальных данных, используем следующую схему расчета вырождения диаграммы деформирования при ступенчатом изменении максимальной деформации цикла.

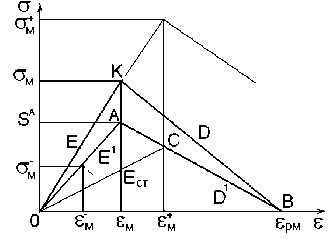
Рис. 4. Схема перехода на новую деформацию цикла при n>N

Пусть в состоянии материала, полученном при циклировании на уровне максимальной деформации цикла E M и определяемом диаграммой ОАВ (рис. 4), ступенчато увеличивается максимальная деформация цикла от E M до e M . Новое состояние ОСВ сопровождается падением сопротивления на величину A S и модуля упругости до величины E_CT

^{A S} CT = D ^{( E} M ^{- E} M ) ; ^E CT = D^{( E} PM ^-E M ^{)l E} M . (6)

Обозначение A S_CT и E_CT подчеркивает, что падение прочности и новый модуль связаны со статическим переходом на большую деформацию, а не с циклической нагрузкой. При уменьшении максимальной деформации цикла до E M свойства материала не меняются и описываются диаграммой ОАВ. В случае многоосного напряженного состояния под напряжениями и деформациями принимаются интенсивности этих величин.

Имея приведенные соотношения и усталостную кривую в форме N g " = C , перейдем к определению остаточной долговечности ослабленной зоны составного диска, которая находится в условиях однородного напряженно-деформированного состояния и пропорционального нагружения. Сформулируем краевую задачу расчета ресурса составного диска.

При известной геометрии диска, нагруженного на границе Г 2 (рис. 2) заданными перемещениями или равномерно распределенными силами, изменяющимися в стационарном режиме, требуется определить долговечность ослабленной зоны N_P и напряженно-деформированное состояние диска после произвольного числа циклов на заключительной стадии циклирования N <  n <  N _P .

Для решения задачи имеем систему уравнений:

d a r dr

^a r

a0

= 0 - уравнение равновесия;

r

du u

E =-- , E„ = —; - соотношение Коши;

r ,        0

dr r

• -    физические уравнения (1);

• -    модель усталостного повреждения материала (3-6), (7);

• -    кривая Велера при мягком нагружении N a " = C ;

• -    Г.У. u = u_M (1 - |cos kt\ ) или q = q_M (1 - |cos kt |).

Искомые величины ar, a g, Er и E g зависят от числа циклов нагружения n и значения u или q на границе. При n = 0 решение задачи (7) известно uE

u

2 v

a =a =------,E = E =—,E =--E (8)

r 0                    , r У , z

(1-v)R2         R2       1-v и совпадает с упругим решением. Напряженно-деформированное состояние диска однородно, что дает

ar = Gg = ai, Er = E0 = (1 - V)Ei . (9)

В результате ослабления центральной зоны, т.е. изменения параметров упругости внутреннего диска, напряженно-деформированное состояние в нем станет отличаться от состояния внешнего диска. В этом случае перемещение в составном диске ищется в виде ur = <

' Ar ,0 <  r <  R 1

C

Br + -, R 1 <  r <  R 2 .

I r

Соответственно, неоднородное напряженно-деформированное состояние диска имеет вид:

E = <  r

' A ,0 <  r <  R 1

C

B ^- —, ^R 1 <  ^r <  ^R 2 ,

I r

^E 9 = ‘

A , 0 <  r <  R 1

C

B ⁺ 2^R ^R 1 <  ^r <  ^R ₂ , r

О r = 1

E ¹ A ^ V¹ ^ ,0 <  r <  R

1 -V ?              ¹

—2- I B - - + V 2 I B + -II , R 1 <  r <  R 2 ,

1 -V ? к     r ²     к     r ² ))

^O 9    1

I V    ,0 <  r < ^R .

Д ( B ^{+ - +V} 2 [ B ^-

-2II , R 1 <  r <  R 2 , r ))

где E 1 , V 1 и E ₂ , V ₂ - параметры упругости внутренней и внешней зон. Параметры A , B , C определяются из граничных условий на внешней границе и из условия непрерывности на границе зон перемещения и напряжения в радиальном направлении.

Очевидно, что в интервале стационарного циклирования ( 0 <  n <  N ) условие (2) выполняется, а решение (9) неизменно. Равенство в условии (2) связывается с началом стадии разрушения материала ослабленной зоны. Согласно принципа устойчивости тела в целом [6], эта стадия может протекать равновесно, если возможны равновесные состояния кусочно-однородного диска при n >  N .

Получить точное аналитическое решение задачи (7), отвечающее положению равновесия диска, невозможно. Это связано с тем, что снижение модуля упругости при n = N + А n циклов и снижение сопротивления материала центральной зоны приведут к нарушению условия (2) и к статическому перераспределению напряжений и деформаций в диске, аналогично описанному выше (схема на рис. 4). Что, в свою очередь, приведет к снижению модуля упругости и вызовет новое перераспределение напряжений: задача становится связной. Для ее решения применим пошаговую процедуру догружения с проверкой устойчивости напряженного состояния диска на каждом шаге А n циклического догружения. Проверка выполняется методом последовательных приближений.

На первом шаге по формулам (5) находятся константы материала центральной зоны после n = N + А n циклов, одинаковые во всех точках ввиду однородности напряженного состояния. Решается задача (7) для составного упругого диска при новых константах в физических уравнениях (1) для центральной зоны. Находится решение (10) и интенсивность напряжений в центральной зоне. Проверяется условие (2), находятся интенсивности напряжений и деформаций, необходимые для корректировки упругих констант материала центральной зоны по формулам (6). Снова решается задача (7), проводится корректировка констант для однородно деформированной центральной зоны и т.д.

Если итерационный процесс сходится в области положительных напряжений с любой наперед заданной точностью, то диск после А n циклов и статического перераспределения напряжений имеет новое положение равновесия и новые упругие свойства материала центральной зоны. Возможно циклирование с новой амплитудой деформаций в течение следующих А n циклов. Такой прием с остановкой циклирования вполне оправдан ввиду несоизмеримо разных физических времен процессов накопления усталостных повреждений и перераспределения напряжений в упругом теле. Обычно полагается, что последний процесс проходит практически мгновенно. Наружное кольцо и центральный диск остаются упругими, но поскольку сходимость итерационного процесса зависит от свойств материала и от геометрии конструкции, то остаточная долговечность также зависит от этих факторов. Для наглядности параметрического анализа рассмотрим числовой пример расчета долговечности N _P диска с учетом состояний разупрочнения, в котором полагалось:

Радиус наружного кольца R ₂ =0,1 м.

Радиус центрального диска R ₁ =0,03 м.

Модуль упругости        E = 2 - 10 5 МПа.

Коэффициент Пуассона у =0,3.

Показатель усталостной кривой а =6.

Показатель кинетической кривой m =2.

Максимальная нагрузка цикла               qM =85,714285 МПа.

Максимальное перемещение u_M = 0,00003 м.

Соотношение модулей упругости и хрупкости                   E / D =2.

На рис. 5 приведены результаты расчета тангенциальных и радиальных напряжений в составном диске при максимальном значении цикла нагрузки q_M (левая часть) и максимальном перемещении u_M (правая часть), подобранных из условия равенства напряжений в исходном состоянии. В первом случае протяженность этапа разупрочнения N_P =440 циклов, а во втором N _P =5750 циклов. В обоих случаях нагружения уменьшение начального модуля хрупкости, равнозначное повышению трещиностойкости материала, приводит к увеличению долговечности. Так увеличение отношения E / D до 5 увеличивает стадию разупрочнения до 1450 циклов в первом и до 6270 циклов во втором случае, соответственно. Число итераций при установлении положения равновесия сокращается в 3 и в 1,2 раза.

Равенство СТ_в = ( T r имеет место во всем диске до числа циклов n=N, а затем, при сохранении однородности напряженного состояния, напряжения в центральной ослабленной зоне падают до нуля (при числе циклов n = N + N P ). Задача о составном диске переходит в задачу Ламе, так как по условию задачи наружное кольцо остается упругим. Штрихами на рис. 5 показано промежуточное состояние диска при n = N + 0,5 N P .

Влияние геометрии конструкции, задаваемое отношением радиусов R ₁ / R ₂ (при фиксированном

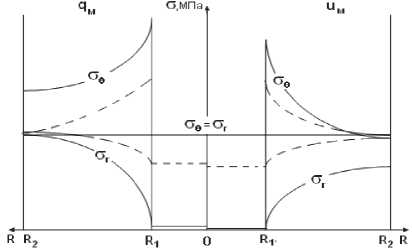
Рис. 5. Распределение тангенциальных и радиальных напряжений в составном диске на стадии циклического разупрочнения значении R 2 ) и определяющей жесткость системы нагружения центральной зоны, поясняет рис. 6.

Продолжительность стадии разупрочнения N _P невелика и при заданном на границе перемещении выше, чем при заданном напряжении. В первом случае уменьшение толщины упругого кольца, то есть увеличение отношения R 1 / R 2 , приводит к увеличению N_P , а во втором к снижению числа циклов до разрушения. Такая закономерность наблюдается до значения R 1 / R 2 =0,55. Далее отмеченный выше итерационный процесс не сходится, так как жесткость системы, передающей нагрузку в центральную зону и представленной в данной задаче упругим кольцом, становится недостаточной для реализации реологически неустойчивых состояний материала.

Таким образом, устойчивость процесса циклического разупрочнения материала в элементе конструкции зависит как от свойств материала, так и от условий нагружения. В модельной задаче о долговечности составного диска показано, что продолжительность стадии разупрочнения N_P зависит с одной стороны от трещиностойко-сти и скорости циклического разупрочнения материала, а с другой от вида граничных условий и жесткости системы нагружения зоны разрушения, то есть от геометрии конструкции. Разрушение центральной зоны может выглядеть как хрупкое, если упругое кольцо тонкое, или как вязкое, при достаточно толстом кольце. Отметим, что в статически неопределимой системе неустойчи-

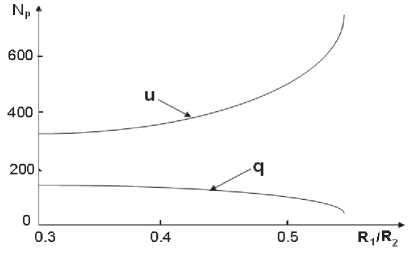
Рис. 6. Влияние типа граничных условий и соотношения размеров упругого кольца и центральной зоны на продолжительность стадии разупрочнения вые циклические состояния в разрушающемся элементе реализуются как при заданных на границе перемещениях (кинематическое нагружение), так и при заданных силах. Принятое в расчетной схеме (рис. 3) условие кинематического нагружения не существенно сужает область реализации циклического разупрочнения, так как большинство задач теории упругости и строительной механики статически неопределимы.