Модель деформации пятислойной панели с жестким заполнителем

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2019PNRPU MECHANICS BULLETIN

В настоящее время промышленность проявляет все больший интерес к многослойным сотовым конструкциям с различного типа заполнителями [1–32] и, в частности, к пятислойным конструкциям с жестким заполнителем, так называемым биконструкциям. Использование для оценки напряженно-деформированного состояния метода конечных элементов при всех его преимуществах требует верификации расчетных моделей. Необходимо отметить, что верификация конечноэлементных моделей многослойных панелей на основе прямого эксперимента затруднена из-за невозможности задания граничных условий на торцах многослойной панели, что приводит к значительным погрешностям в напряжениях на ее концах [1]. Особенно это касается вопросов исследования механических свойств панелей, когда они испытываются как балочные элементы при трехточечной схеме нагружения. Поэтому для верификации конечно–элементных моделей целесообразно использовать аналитические модели. При построении аналитических моделей используются, как правило, два подхода. Первый основывается на рассмотрении элемента конструкции при статическом равновесии выделенного элемента панели, второй, на основе вариационного принципа Лагранжа, преимуществом которого является возможность непосредственного нахождения естественных граничных условий.

Исследование многослойных конструкций с прямолинейной и круговой осью, как правило, требует введения гипотез о перемещениях и напряжениях по толщине панели. Поэтому многочисленные исследования по напряженно-деформированному состоянию многослой- ных панелей, в особенности за рубежом, посвящены нахождению различных приближенных решений путем аппроксимации функций перемещения полиномами от переменной, изменяющейся по толщине, в слоях многослойной панели. Анализ литературы [16–30] показал, что для аппроксимации могут использоваться различные типы элементарных функций: полиноминальные [29], тригонометрические [20–23], гиперболические [24], а также их комбинации [25]. В [18] проанализировано 246 работ зарубежных и отечественных авторов, которые посвящены вопросам расчета многослойных панелей с применением как аналитических, так и конечно-элементных моделей. За последние 5 лет в [16] проанализировано 515 работ зарубежных авторов, посвященных вопросам построения аналитических многослойных балочных моделей статической прочности, частот собственных колебаний и устойчивости. Обзор моделей с сотовым заполнителем представлен в [17].

Из проведенного анализа следует, что задача верификации конечно-элементных моделей на основе разработки аналитических моделей напряженно-деформированного состояния многослойных панелей при тех или иных допущениях относительно поперечных и касательных напряжений по толщине слоя заполнителя не потеряла своей актуальности. Особенно это касается практического применения при расчете биконструкций, используемых при проектировании летательных аппаратов.

1.    Постановка задачи

В работе ставится задача верификации конечноэлементной модели прогиба пятислойной панели с жестким заполнителем при ее нагружении поперечны- ми и продольными равномерно распределенными силами с помощью аналитической модели.

2.    Решение вариационной задачи

Рассмотрим многослойную панель, размерами ( 0, a ) вдоль координатной оси X и ( 0, b ) вдоль оси Y . Пусть поперечный прогиб панели описывается функцией w ( x , y ).

Рассмотрим вариационную задачу относительно функционала

J ( w ) = ff F ( x , y , w , w x , w y , w Z , w xx , w xy , w yy ) dxdy  (1)

в прямоугольнике [ 0, a ] ^x [ 0, b ] с искомой функцией w ( x , y ) . Для удобства изложения введем следующие обозначения для производных:

Р = w x , q = w y , A = w x , B = w xy , C = w yy .

Предполагается, что искомое решение w(x, y) на горизонтальных и вертикальных отрезках прямоугольника [0, a]х[0, b] удовлетворяет граничным условиям Дирихле w (x, 0) = f) (x), w (x, b) = f1 (x), w (0, y) = g0 (y), w (a, y) = gi (y)

или граничным условиям Неймана wY (x, 0) = f) (x), wY (x, b) = f. (x), wX (0 y) = g0 (y), wX (a, y) = gi (y)■

Поскольку в последующих вычислениях повсеместно применяются выражения, использующие суперпозицию с функцией и ( x , y ), громоздкие выражения вида

F [ x , y , w ( x , y ) , w X ( x , y ) , w Y ( x , y ) , ^w Xx ( ^x , y ) , ^w X ( ^x , y ) , ^w YY ( ^x , y ) ] , целесообразно редуцировать до более кратких выражений вида F ( x , y ) , для которых функция w ( x , y ) и ее производные до второго порядка не записываются, но предполагаются.

Обозначим через w = f ( x , y ) решение вариационной задачи, получим дифференциальное уравнение и набор граничных условий, которым оно должно удовлетворять. Обозначив через ф = ф ( x , y ) вариацию для независимой переменной а , рассмотрим возмущенное решение вида w ( x , y , а ) = w ( x , y ) + аф ( x , y ) .

Из предположения, что функция w ( x , y , а ) является решением вариационной задачи, следует, что функция

L ( а ) = J ( w +аф ) при а = 0 имеет минимум по переменной а :

ab

• L' ( 0 ) = Л( F w Ф + F P Ф X + F q Ф Y +

• ^{+ F} A ^ф XX ^{+ F} B ^ф XY ^{+ F} C ^ф YY ) ^dxdy = ^0.

Интегрируя по частям, получим выражение для производной в виде ab

• L ‘ (0)   ff ( F w - F px - F qy + F Axx + F Bxy + i™ ) ф dxdy +

b

+ f ( ^F P ^{( a} , y ) - ^F Ax ^{( a} , y ) - ^F By ^{( a} , y ) ) ф ^{( a} , y ) dy ^-

0 b

• - f ( F p (0, y ) - F AAx (0, y ) - F By (0, y ) ) ф (0, y ) dy +

0 a

⁺ f ( ^F q ^{( x} , ^b ) ^{- F} Bx ⁽ x , ^b ) ^{- F} Cy ⁽ x , ^b ) ) ф ⁽ x , ^b ) ^{dx -}

0 a

• - f ( F q ( x , 0) - F Bx ( x , 0) - F Cy ( x , 0) ) ф ( x , 0) dx +

bb

+ f ^F A ^{( a} , y ) ф x ^{( a} , y ) dy ^- f ^F A ^(0, y ) ф x ^(0, y ) dy ⁺ 0                           0

+ ^a F C ( x , b ) ф y ( x , b ) dx - f F C ( x , 0) ф y ( x , 0) dx + 0                           0

+ F B ( a , b ) ф ( a , b ) - F B ( a , 0) ф ( a , 0) -- F B (0, b ) ф (0, b ) + F B (0,0) ф (0,0) = 0.

Для получения дифференциального уравнения в частных производных возьмем вариацию ф , равную нулю на периметре прямоугольника [ 0, a ] ^х [ 0, b ] . Из произвольности вариации ф следует, что искомое решение w должно удовлетворять дифференциальному уравнению

F w - F px - F qy + F Axx + F Bxy + F Cyy = 0.      (2)

Пусть на решение w наложены граничные условия Дирихле. В этом случае выбор вариации ф в рамках однородных условий Дирихле

ф(x,0) = ф(x,b) = 0, ф(0, y) = ф(a, y) = 0, может быть произвольным. В частности, варьируя производные по ф на периметре прямоугольника [0, a]х[0, b], дополнительно к условиям Дирихле получим граничные условия вида

F C ( x , 0 ) = F C ( x , b ) = 0, F A ( 0, y ) = F A ( a , y ) = 0. (3)

Пусть на решение w наложены граничные условия Неймана. В этом случае, выбрав вариации φ в рамках однородных условий Неймана, получим

фy (x,0) = фy (x, b ) = 0, фx (0, y) = фx (a, y ) = 0.

В частности, варьируя значения ф на периметре прямоугольника [ 0, a ] x [ 0, b ] дополнительно к условиям Неймана, соотношение для естественных граничных условий запишем на периметре панели:

F q ( x , 0 ) - FB_x ( x , 0 ) - F ^ ( x , 0 ) =

• =    F^(x,0)-FBX(x, b)-FC(x,b) = 0,

f ; ( 0, y ) - FA_x ( 0, y ) - F^( 0, y ) =

• =    F'p (a, У)- fax (a, У)- fby(a, У ) = 0

• 3. Аналитическая и численная модель изгиба пятислойной панели

и для условий в углах панели

[ 0, a ] x [ 0, b ]

FB (0, 0) = FB (a, 0) = FB (0, b) = FB (a, b) = 0 .(6)

Таким образом, выражения (4)–(6) отражают естественные граничные условия. Следует отметить, что в классической теории панелей [11] условие (6) не рассматривается.

Проиллюстрируем предложенный подход нахождения естественных граничных условий в задаче оценки изгиба пятислойной плоской панели с последующей верификацией ее конечно-элементной модели для двух наиболее важных для практики случаев нагружения: равномерно распределенными по кромкам нагрузками в плоскости панели с интенсивностью p , p и поперечной равномерно распределенной нагрузкой интенсивностью Q . Для этого рассмотрим прямоугольную пятислойную панель (рис. 1, а ) шириной a и длиной b и тремя несущими обшивками с толщинами 1 i = ₁ , ₂ , ₃. Материал обшивок изотропный с модулями упругости E и модулем сдвига в плоскости обшивок G . Слои заполнителя не сопротивляются изгибу и являются абсолютно жесткими при поперечном сдвиге и поперечном сжатии. Зависимость между относительными деформациями и перемещениями описывается с помощью соотношений Коши.

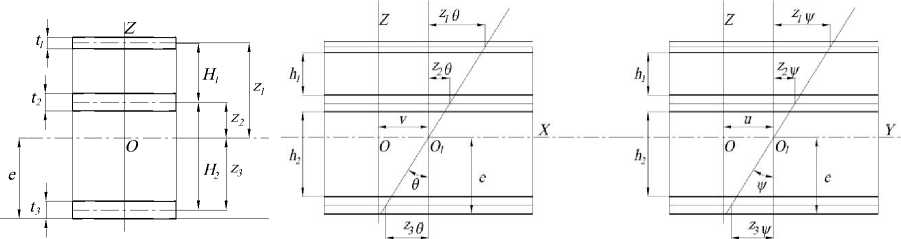
а                                                 б

Рис. 1. Геометрические размеры пятислойной панели ( а ) и перемещения элементов панели вдоль осей OX , OY (б )

Fig. 1. Geometrical sizes of the five-layer panel ( а ) and displacement elements of the panel along axes OX , OY (b )

В соответствии с гипотезой плоских сечений углы поворота панели вокруг осей OX , OY равны:

S(x,У) = -wX, v(x,У) = -Wy, где w (x, y) - перемещение панели вдоль оси OZ (рис. 1).

Перемещения обшивок панели по оси X в соответствии с гипотезой плоских сечений (см. рис. 1) можно записать в виде

• —    ( i = 1 ) ^V 1 ( x , У ) = v ( x , У ) + Z 1 ⁹ ( x , У ) =

= ^v ( ^x , У ) ^- ( H 1 ⁺ H 2 ^- e ^{+ 1} 3/² ) ^W X ,

• ^-    ( i = ² ) ^v 2 ( ^x , У ) = ^v ( ^x , У ) ^{+ z} 2 ^ ( ^x , У ) =

= ^v ( ^x , У ) ^- ( H 2 ^{+ 1} з/ ^{2 - e} ) w X ,

• -    ( i = 3 ) V 3 ( x , y ) = v ( x , y ) + z 3 » ( x , y ) =

= v ( x , y ) + ( e - 1 3/2 ) w X .

При этом координата z срединной поверхности (рис. 1, б )

e = [ ( H 1 + H 2 + 1 3 /2 ) t 1 +

^{+ (} H 2 ^{+ 1} 3 / ^{2 ) 1} 2 ^{+ 1} 2 / ²]/ ^{( 1} 1 ^{+ 1} 2 ^{+ 1} 3 ) •

Аналогичным образом записываются перемещения u i ( i = 1,2,3 ) вдоль оси У .

Для вывода дифференциальных уравнений используем функционал, равный сумме потенциальной энергии деформации панели и работе внешней силы:

( D 2 ( u'x + V y ) + D 1 ( ( u X ) + 2 ц U y v X + ( v ‘ x ) ) ) +

F = ¹

+ ( D ₃ [ ( w X ) ² + 2 ц v X w y + ( W y ) ² ] + 4 D ₄ ( w XY ) 2 ) +

. .(7)

^{+ 2 [} Qw ( x , y ) ⁺ P x v ( X , y ) ⁺ P y u ( ^x , y ) ]

В выражении (7) приняты следующие обозначения:

^D 1 =; y^{( 1} 1 ^{+ 1} 2 ^{+ 1} 3 ) , ^D 2 = G ^{( 1} 1 ^{+ 1} 2 ^{+ 1} 3 ) ,

1 -ц

^D 3 — p E r

^{1 -}Ц

⁽ Н ! + H 2 ) t i t 3 + H ! t i t 2 + H 2 t 2 t 3

t 1 ⁺ t 2 ⁺ t 3

3 I 3

+ У| — mI 12

D ₄ = G

⁽ H 1 + H 2 ) t i t 3 + H 1 t i t 2 + H 2 t 2 t 3

t 1 ⁺ t 2 ⁺ t 3

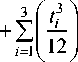
a f a w X	1 0 J X	— D 3	y 2       л2 I a w      a w I     _ _       3   _ |— + H-r| — M x ( 0 , y ) — 0 , (a x      a y jo
'S F' va w,	y )   — a	; D3 (	2      д2 a w      a w ।          z     3 n    ...... +ц^л) — M x ( a ’ y ) — 0; (11) a x      a y jo

где ц - коэффициент Пуассона.

Необходимо отметить, что гипотеза плоских сечений применима для панелей, отношение ширины которых к толщине больше пяти [31].

Записав уравнение (2) для каждой из функций u , v , w (7), получим следующую систему дифференциальных уравнений:

– удельные силы давления R на кромки панели x — 0, x — a a I af I a (af Iy  Dzn 3

lI+l        I — R (0, y) — ay(awXY J  ax(awY Jo

• — ( 4 D 4 + D , ^ )f f| 2 w 1+ D , f| 3 w I — 0,    (12)

ax (ay J     (ax J aF didF

---- av  ax(avX a ay

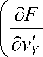
— D1 vXX + (D2 + D1^) u XY + D2 vYY  Px — °’ aF  didF1 didF1 _

----------- — au  ax (auX J  ay (au'Y J

— D2uXX + (D2 + Дц) vXY + D1 uYy - Py — 0, aF  a2 IdF 1  d2 IdF 1  d2

+--rl „    1+--tI     „ l + - 1„ I aw  ax2 (awxx J  ay2 (awYYJ  axy (awX J d4w /           x a4w      a4w

— D 3 . . + ( 4 D 4 + 2 А^ТгТГ + D 3 TT + Q = °'

a x ⁴                  a x ² a y ²       a y ⁴

Первые два уравнения описывают перемещения панели по осям X , Y , а третье - перемещение от поперечного изгиба вдоль оси Z .

Естественные граничные условия для оси X могут быть получены с использованием выражений (3)–(6):

– нормальная составляющая силы, N приложенная в направлении оси OX на сторонах x — 0, x — a

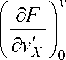
y

_ I d v     d u I ..      3 _n

^— D I l -  ¹ Ц I ^— N x ( °’ y ) ^{— 0} ,

I a x     d y L

°

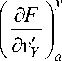
y

| d v     d u I         z 3

^{— d} 1|^⁺^tI ^— N x ( a ’ y ) ^{— 0};

i a x    a y j

a

- касательная составляющая T на сторонах x — 0, x — a

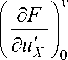
y

— D ₂1 ^ v +ц— I — T ( 0, y ) — 0, ² (a y    a x J_o    '••    ’

	' a f "	a	y a f I           \ ----- — R ( a , y ) —
a y 1	. a w Xy,	J   a x 1	a w ’ j Xa

— ( 4 D 4 + D 3 _Ц)^ Г| 2 2 2 1 + D 3 Г^ 1 — 0;    (13)

a x I a x ² J       (a x³ J

– силы H в углах панели, уравновешивающие крутящие моменты на ее кромках

a f a w XY	1   — H ( 0’0 ) — 4 D 4 J x — 0, y — 0	a 2 w (a y a x	x — 0, y — 0	— 0,
a f a w Xy	1   — H ( 0’ b ) — 4 D 4 J x — 0, y — b	I a 2 w (a y a x	x — 0, y — b	— 0,	(14)
a f a w XY	)   — H ( a ,0 ) — 4 D 4 J x — a , y — 0	I a 2 w (a y a x	1 ) x — a , y — 0	— 0,
a f a w Xy	)   — H ( a , b ) — 4 D 4 J x — a , y — b	I a 2 w (a y a x	J ) x — a , y — b	— 0.	(15)

Получение естественных граничных условий по оси Y аналогично.

Рассмотрим решения (8) для наиболее часто используемых в практике способов закрепления панели.

Пусть p – равномерно распределенная по граням нагрузка приложена к кромке x — a по оси OX , а p_Y -к кромке y — b по оси OY . По кромкам x — 0, y — 0 панель закреплена в направлении осей OY и OX .

Решение первых двух уравнений системы (8) можно записать в виде

v ( x ) — C 1 + C ₂ x ; u ( y ) — C ₃ + C ₄ y .        (16)

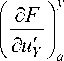
— D 2

I a v a u I y l ~+~ I (a y a x i a

^{— T} xy ( a ’ y ) ^{— 0};

Константы C ... C₄ находятся из естественных граничных условий:

– изгибающие моменты M на кромках панели x — 0, x — a

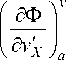
I a v     d u

— D 1 1 — + ц—

(a x    a y

y

— p_xa ,

a

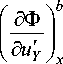
b

I d u      d v i

— D I--+ ц — I d y    d x

x

^— P y b .

Окончательно функции перемещений v ( x ), u ( y )

вдоль осей X , Y преобразуются к виду

^{v ( x} ) ^—

аР х -Ц bp Y D ( 1 -ц ² )

u ⁽ y ) ^—

ap y - Ц bp x D i ( 1 -Ц ² ) y .

t i _— i 2 з принимались соответственно равными 1, 2, 3 мм. Модуль упругости несущих обшивок 2×10⁵ МПа, а модуль сдвига в плоскости несущих обшивок 10⁴ МПа. Толщина слоя первого заполнителя принята равной 15 мм, второго – 10 мм. Панель нагружена в плоскости равномерно распределенными силами с интенсивностью p_x — p_Y — 10 H/мм, приложенными к ее сторонам, а также равномерно распределенной нагрузкой с интенсивностью Q = 0,1 МПа. Для построения конечно-

Последнее уравнение системы дифференциальных уравнений (8) для равномерно распределенной нагрузки решается методом Навье и может быть представлено двойными тригонометрическими рядами. Сходимость двойных тригонометрических рядов продемонстрирована в [11].

Для поперечных прогибов точность в 1 % достигается удержанием 4-го члена ряда, а для изгибающих моментов (напряжений) точность в 2 % достигается удержанием не менее 200 членов ряда.

Функция w ( x,y ) позволяет найти все параметры напряженно-деформированного состояния панели, а с помощью выражений (9)–(15) можно получить реакции и удельные силы давления по кромкам панели, силы в углах и уравновешивающие крутящие моменты на кромках, отражающие влияние краевого эффекта .

Для верификации конечно-элементной модели пятислойной панели использовались результаты аналитического расчета пятислойной квадратной панели со сторонами а — b — 250 мм. Толщины несущих обшивок элементной модели использован элемент многослойной оболочки Shell 181. Одним из основных параметров указанного элемента является положение базовой поверхности, от которой производится отсчет координат z для всех слоев по толщине панели.

Для случая нагружения панели в плоскости равномерно распределенными силами с интенсивностью p_x , p_Y , приложенными к ее граням, было выполнено сравнение аналитического и численного решения, полученного с использованием неверифицированной конечно-элементной модели. Сравнение показало, что максимальные перемещения вдоль осей OX, OY не совпадают. При этом они распределены нелинейно, а перемещения вдоль вертикальной оси OZ отличны от нуля. Нормальные напряжения по толщине несущих обшивок также распределены нелинейно. Эпюры углов поворотов поперечных сечений отличны от нуля. Это означает, что панель кроме растяжения испытывает также изгиб. Указанные отличия обусловлены смещением базовой поверхности относительно срединной поверхности (рис. 2).

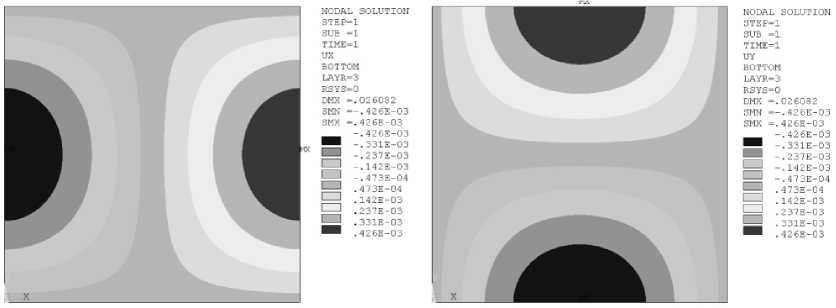
а

б

Рис. 2. Эпюра перемещений базовой поверхности вдоль осей OX ( а ), OY ( б ) до верификации конечно-элементной модели

Fig. 2. Epure of displacements of a base surface along axes OX ( a ), OY ( b ) to verifications of the finite-element model

Чтобы базовая поверхность стала срединной поверхностью, ее необходимо сместить на величину, равную отношению максимального перемещения ( UX max ) вдоль оси OX к максимальному углу ( R ot Y max ) поворота вокруг оси OY :

z — UX RotY —- 0,426 • 10 ^{- 3} /0,341 - 10 ^{- 3} —- 1,25. max max

При таком смещении базовой поверхности результаты по аналитической и конечно-элементной модели совпали с приемлемой для инженерных расчетов точностью. Следует отметить, что если сечение панели сим- метрично относительно ее базовой поверхности, то различий между аналитическим и конечно-элементным решениями не возникает, так как в этом случае базовая поверхность панели является и ее срединой поверхностью. Таким образом, при верификации двухмерной конечноэлементной модели пятислойной панели, нагруженной силами, действующими на ее кромки, необходимо совмещение базовой поверхности со срединной поверхностью.

При нагружении панели (рис. 3) поперечной равномерно распределенной нагрузкой (шарнирное закрепление) после смещения базовой поверхности погрешность определения значения максимального прогиба по конечно-элементной модели и аналитической модели не превысила 0,27 %. Погрешность расчета нормальных касательных напряжений, реакций и напряжений в данном случае не превысила 1,3 %.

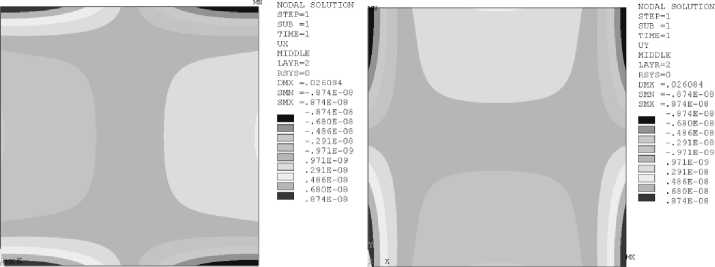
б

Рис. 3. Эпюра перемещений базовой поверхности вдоль осей OX ( a ), OY ( б ) после верификации конечно-элементной модели

Fig. 3. Epure of displacements of a base surface along axes OX ( a ), OY ( b ) after verification of is finite-element model

Таким образом, верификация конечно-элементной модели прогиба пятислойной панели аналитической моделью дает хорошее совпадение аналитического и численного решений.

Область применения аналитической модели распространяется на стадию эскизного проектирования, а верифицированной конечно-элементной модели – на стадию опытно-конструкторских работ по созданию пятислойных панелей с жестким заполнителем, относящихся к классу биконструкций.

Заключение

• 1.    Областью применения предлагаемой модели является оценка напряженно-деформированного состояния панели пятислойной биконструкции, которая характеризуются наличием поясов (обшивок), воспринимающих изгибающий момент и оказывающих основное