Модель деформирования ДКБ-образца с упругопластическими свойствами

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2021PNRPU MECHANICS BULLETIN

Экспериментальное исследование трещиностойко-сти материалов использует в качестве образца для изучения трещины нормального отрыва двухконсольную балку (ДКБ-образец). На образцы и порядок проведения испытаний действует соответствующий регламент, определяемый по ГОСТу. В процессе испытаний определяется критическое значение коэффициента интенсивности напряжений (КИН) – вязкость разрушения K [1–3]. При этом используется определение КИН в рамках классической модели трещины, рассматриваемой в виде математического разреза в линейно-упругой среде. Непосредственно измеряемой характеристикой данного эксперимента является зависимость расклинивающего усилия от перемещения, в которой выделяются линейный и нелинейный участки. Для выяснения причины нелинейности необходимо проводить промежуточные разгрузки с целью выявления наличия пластических деформаций либо их отсутствия. Учет возможной физической нелинейности, обусловленной пластичностью, находит отражение в моделях трещины нулевой толщины путем введения поправки Ирвина – Орована [4, 5], сил сцепления [6–12], тонкой пластической зоны [13, 14], пластического коэффициента интенсивности напряжений [15], поперечника пластической области [16, 17]. Как правило, образование пластической зоны в этих моделях происходит с начала нагру- жения, а стадия чисто упругого деформирования не отражается.

Классическая постановка упругопластической задачи [18–21] подразумевает наличие условия перехода материальной области из упругого состояния в пластическое. Если область не содержит источников сингулярности напряжений, то из решения упругой задачи определяется внешняя нагрузка, при которой достигается предел упругости. В этом случае в рассмотрение вводится модель трещины в виде физического разреза [22]. Модель упругого деформирования трещины в виде физического разреза может быть рассмотрена на основе связей Прандтля [23–26], однако вопрос о выборе характерного размера и жесткости связей открыт. В работах [27–31] рассмотрена модель, основанная на концепции слоя взаимодействия, для которой материальные свойства слоя соответствуют поврежденному телу, а характерный размер определяется из решения обратной задачи [30].

В данной работе на основе общей вариационной постановки [30] получено упрощенное аналитическое решение задачи деформирования двух упругих тел, связанных тонким слоем с упругопластическими свойствами. Рассматривается процесс упругопластического деформирования при неизменной длине слоя. Полученное решение в упругой области не содержит осцилляций, в отличие от решения в балочном приближении [28]. Показано, что при классическом условии текучести диапазон внешней нагрузки, приводящей к чисто упру- гому поведению, возможен только при конечной толщине слоя. При стремлении толщины слоя к нулю, как и в задаче Дагдейла, область пластичности образуется при сколь угодно малой внешней нагрузке. Для малых толщин слоя, вплоть до нулевых, предложен локальный критерий пластичности, при использовании которого возможно выделение внешних нагрузок, связанных с упругим и пластическим деформированием. Из анализа экспериментальных данных [32] приведена оценка зоны пластического деформирования при использовании локального критерия.

Постановка задачи нормального отрыва

j о - -5 s ds - j n₂₂5u₂ dx_} - j c₁₂5u₇ dx +

S 2

i       d5 u d5 u i        2

+ 0.55_o jc₇₇--- -dx ₇ +j^₇₂--- ~dx  = J p *5 U dl , (2)

0 (    ¹¹ d x     ^{1      12} d x     ¹ J l

где S , S – площади тел 1 и 2; σ , ε – тензоры напряжений и деформаций; σ , ε – тензоры средних напряжений и деформаций слоя с компонентами: g_2] ( x ) = g₁₂ ( x ) =

^   O.5 5 o

=       j ^ 21 ⁽ x i , x 2 ) ^dx 2 ,

⁵ 0 - 0.5 5 0

^   O.5 5 o

^ 22 ( x i ) = Г J ^C 22 ( x i , x 2 ) dx 2 ,

0 - 0.5 5 ₀

На рисунке показана двухконсольная балка (ДКБ-образец) I + a , состоящая из трех тел. Пластины 1 и 2 с одинаковыми толщинами h по длине связаны слоем взаимодействия 3 толщиной 5₀. Материал пластин принимаем линейно-упругим, а материал слоя взаимодействия – идеально упругопластическим. Пластические деформации слоя ограничены длиной _p . Правый торец образца жестко закреплен от горизонтальных и вертикальных перемещений, на левых торцах консолей действует вертикальная симметричная нагрузка интенсивностью P . Вся остальная поверхность образца свободна от внешней нагрузки.

^   0.5 5 0

^ 11 ( x i ) =       j   ^CT 11 ( x i , ^x 2 ) dx 2

⁵ 0 - 0.5 5 ₀

⁸ 22 ^{( x}1 ) =

' u + ( x , ) ^- u - ( ^x 1 )

, ,       fd u + ( x.)    d u, (x ,))

^! ( x = 0.5      ^{1 ( 1} ) +    ^{1 ( 1} )

^{41V u}     I   d x       d x  J

^S 21 ^{( x} 1 ) = ^S 12 ^{( x} 1 ) =

= 0.5

^{f u} 1 ⁺ ( ^x 1 )^{- u} 1 ^- ( ^x 1 )

+ 0.5

fy u + ( x ,) _v   d x

d u j ( x ) d x

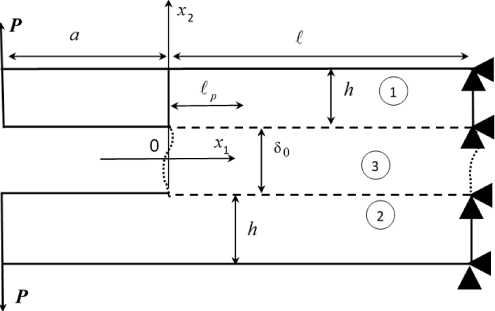
Рис. Модель ДКБ-образца

Fig. Model of the DCB-sample

Для описания взаимодействия слоя 3 с телами 1 и 2 применим концепцию «слоя взаимодействия», развитую в работах [24–29]. В этом случае условия равновесие тел 1 и 2 запишем в вариационной форме:

– для тела 1 :

j о - -5s ds + j Q₂₂5 u + dx_} + j с₁₂5 u ⁺ dx_} +

S 1

где u ± - компоненты векторов перемещений верхней и нижней границ слоя соответственно; к = 1,2; L_x , Ъ₂ -граница приложения внешней нагрузки для тела 1 и 2 . Постулируется жесткое сцепление между границами области 3 и областями 1 , 2 :

u ⁺ = u ( x„ 5 0/ 2 ) ; u ^- = u ( x„ -5 0/ 2 ) x 1 е [ 0;^ ] .

Для материала пластин примем определяющие соотношения в форме закона Гука:

- E f      v

^CT ij ~ (1 + v ) (^S i ⁺ 1 - 2 v

где E , v - модуль упругости и коэффициент Пуассона тела; 8 = е_п + в₂₂ + 8₃₃ - объемная деформация; 5 ij - символ Кронекера; i , j = 1,2,3.

Предполагаем, что напряженное состояние слоя для данного вида нагружения определятся одной компонентой тензора средних напряжений. Для материала слоя взаимодействия 3 определяющие соотношения на стадии обратимого деформирования принимаем в виде ст22 = E3822;стп = СТ12 = 0; ст22 < ^0,

+ 0.55_о

Ij6„

d5 u + , г    d5 u + , ) с _Лi __w ,, _Z1X

--- dx_x + j а₁₂----dx, = J P - 5 U dl (1) d x       ^J     d x,         ;

а на стадии пластического течения –

ст ₂₂ =^ 0 ; ст_п =ст ₁₂ = °

– тела 2 :

где а₀ - предел текучести материала слоя; Е₃ - модуль упругости материала слоя.

Соотношения (6) соответствуют представлению типа упругих связей Прандтля [23], а (7) – модели Дагдейла [14]. В силу симметрии задачи проекции поля перемещений удовлетворяют условиям Ц ( x , x₂ ) = u_x ² ( x_x , x₂ ) = = u ( x , x₂ ) , u₂ ( x , x ₂) = - u 2 ( x , x ₂) = u ₂ ( x , x₂ ) , а вектор распределенной внешней нагрузки - P¹ = - P² = P . Таким образом, достаточно ограничиться рассмотрением тела 1. С учетом того, что в слое взаимодействия для данного нагружения имеет место (6) и (7), система уравнений (1)–(2) преобразуется в вариационное уравнение:

J о - -5sds + J g225u + dx1 = J P - 5 Udl.(8)

S1

Решение системы (5)–(8) сводится к определению поля перемещений u ( x_px₂ ) в теле 1 (см. рисунок) c учетом граничных условий на его торцах:

u2 (xi , X2 )|x      0, u2 (xi , X2 )|x, _,= 0,

^211 x, =-a = 0,C

^12| x, =-a =—P.(

Г - ,      f ^{- 0} h ⁺ + ⁵o/ ²

о - -5 s ds =

J                 J - a J 5 o /2

S 1

° 1

V

d 5 u + dx ₁

( x2

, .d 5ф) ⁵0/ ^{2 )—}T” I ⁺ dx i J

.     ^f d 8 u ₂"   - )),       . t‘ ° - ⁰ r h + '

+ a„ -----5®  dxdx, +x

12 V dx        JJ 1   2   J+0

(    f d8u2   ,     „ MXd5®)      f d8u,2   _ ) ) ,  ,, xl ^n ---~ -(x-i -80/2)---- +^i2 ---~ -5® I dxdx. +

V 11V dx1             0' ’ dx1 J 12 V dx1       'JJ 12

fh+5o/2f   fd5u +  , d _d5®Y    fd5u2-

+           a,, ---- - x. -5_n/2---- +^i_? -----5® dxdx. . ^{v 7}

^J P + о ^JV2 V ¹¹ V dx ^{( 2    0/} ) dx J   ¹² V dx      J) ^{1 2}

Введем в рассмотрение обобщенные силы:

f h +5 0/2

On 6x2 ,

50/2

fh+50/2 O12 dx2,(20)

V ⁵ 0/²

и обобщенный момент:

, x     f h+5n /2

M11 (x1 ) = J$/2  CT11 (x2 -50/2) dx2*

⁵0/ ²

Интегрируем по частям ряд слагаемых в правой части (18) с учетом (19)–(21):

r n      d 5 u ⁺             _ , i x , = n     r n dQn _ ,

J ^Q 1 k —r— ^dx1 = ^Q 1 k ^{5 u}k    ^- f "-T^{u 5 u}k ^dx 1 ,   (22)

^Jm       dx.                 x = m    mm dx.

r n d 5®             x = n    nndM_xx

I ^M 11 —— dx 1 = ^M 11 ⁵ Ф_х__т^-| —-^{22 5}® dx 1 ,   (23)

^J m       dx_x                 x ¹ = ^m    m¹ dx_x

Для упрощения задачи принимаем, что поле перемещений в теле 1 определено следующим образом:

^u1 ( ^x 1 , ^x 2 ) = ^{u +} ( ^x 1 ) -® ( ^x 1 )( ^x 2 ^-5 0/² ) ,       ⁽¹³⁾

u 2 ( x i , x 2 ) = u ⁺ ( x 1 ) .                  (14)

где m,n – соответствующие пределы интегрирования по координате x .

Рассмотрим правую часть (8). Найдем вектор напряжений на левом торце консоли P = - e₁ - о = P e₂ . Работа напряжений составит:

Входящий в представление (13), (14) параметр ® имеет геометрический смысл малого угла поворота материальной нормали к плоскости x₂ = 5₀/2 в теле 1 . Согласно распределению (13)–(14) деформации в консоли будут определяться в виде

5 0/2

J P -5 U dl = J P 5 u₂ ⁺( - dx ₂)

L 1                   h +50/ 2

= Ph5u2'I x1=- a

= Q ₂ 5 u 2⁺L _a.(24)

^du. ( х. )

8 11 ( ^x 1 ^{, x} 2 ) =   ^   ~® ( ^x 1 )( ^x 2 ^-50/ ² ) ,     ⁽¹⁵⁾

Подставив (18), (22)–(24) в (8) и приравняв слагаемые при равных вариациях, приходим к двум системам дифференциальных уравнений:

- для участка x_x e [ - a ;0 ) :

dM H - Q_n = 0, d^2k = 0, dQL = 0, dx            dx       dx

8 12 ^{( x} 1 , ^x 2 ) = ⁸ 12

, _х       f du ⁺ ( x. )      , Y

( ^x 1 ) = 0.5 1   ^dx   ~® ( ^x 1 )

- для участков x e

822 (x1, x2 ) = 0.(17)

dM11           dQ11

,      Q12 = 0,    ,   = 0, i = ^22, dx            dxdx

Выражения (15), (16), как теория Тимошенко [33] и работы [34–36], учитывают сдвиговые деформации и повороты нормалей в теле.

Рассмотрим работу внутренних напряжений для тела 1 с учетом заданных полей деформаций (15), (16):

с условиями сопряжения:

I x 1 =-0;^ p -0

I x ₁ =+0;^ _p +0 ,

ф x 1 =- 0;, p - 0 =ф x 1 =+ 0;, p + 0 ’	(28)
u 2 1 x 1 =-0;^ p -0     u 2 1 x 1 =+0;^ p + 0 ,	(29)
M 111 x 1 =- 0, p - 0 = M 111 x 1 =+ 0. p + 0 ’	(30)
^12 1 x 1 =- 0;£p - 0     ^12 1 x 1 =+ 0;^ p + 0 ’	(31)
^111 x 1 =- 0;/ p - 0    ^111 x 1 =+ 0;/ p + 0 ’	(32)

°I2 lx, =-,, =  62’ (33) SU.- a = 0. (34) M11\„,, = 0. (35) и естественным граничным условиям на левом торце:

На правом торце из (9), (10) с учетом (13), (14) рассматриваем граничные условия:

u 1 x _£ = 0. 1 x 1 —X	(36)
ф|  , = 0. T 1 x 1 =x	(37)
u, " 1     = 0. 2 1 x 1 =Z	(38)

С учетом (15)–(17) и условия плоской деформации

В результате задача (25)-(38), (6), (7) с учетом (41)(43) становится замкнутой относительно трех неизвестных функций: и ₇ ⁺ ( x_x ) , u + ( x₁ ) , ф ( x ₇) .

Решение задачи. Рассмотрим частное решение задачи при v = 0; E = E₃ . Запишем решение (25) при удовлетворении граничных условий (33)-(35):

h             6 ? ( x + а ) 3

u_x = — ф + к 3; u₂ = —-----— + к 1 x + к 2;

¹    2²         6 S            ¹

ф= а + a ( x ,«£+ к 1, Lh     2 S

Dh ³

где к1. к 2, к 3 - постоянные интегрирования, 5 = —^-

•

Общее решение (26) для участка x е ( 0J _р) запишем в виде

u+ + h      , X            + _ g0 x4 _ 2k6  3 —г xi + Dh31 1 x + к 9;     (45) 1 = —ф + к 4 x + к 5; u г = 150.+6к4 - к 71 x2+| 2Dh3 fzo к 6 \ к 8 + — ф V Lh   h     J 2 250x3   6к6  2 . f Dh3   Dh3  1   V V     Lh J 6k4 --к 7 h I x1 + к 8. а для участка x е (lр; ^ :

(8₃₃ = 0) определяющие соотношения (5) запишем в виде

Он = D du^^x ) -ф' ( x )( x 2 ^-8₀/ 2 ) J .      ⁽39)

⁵ 12 = ^L

du + ( x ) dx

,

и + =—ф+ к 10 x + к 11;

u = к 12 e ^{X x} 1 + к 13 e ' ^x + к 14 e ^X 3 ^x + к 15 e '4 x ¹ ;

Ф = к 12 ^fX.- — | e ^x - ^x - + к 13 |X₂- K ¹ | e ^3x - +

V ¹    ^ 1 J            V ²    X 2 J

+ к 14 1 X, - K ¹ I e ^X 3 x ¹ + к 15 1 X. -— I e^{x< x} 1 , 34

V     ^X 3 J           V     ^X 4 J

где D =

E ^{( 1} - ^V)  . ; L =

( 1 + v )( 1 - 2 v )       2 ( 1 + v )

где к 1 - к 15 - постоянные интегрирования; K 1 =---;

h § 0

Запишем выражения обобщенных сил с учетом (39), (40):

(19), (20)

^X 1 =

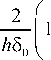
П \ пfz du+   h2

би (xi) = DI h-

V  dx}2

6 § 0 ^{1 h} J

^X 2 = -.

h §

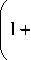
1 - -

6 § 0 I

h

^X 3 =

^1 -

2 h§^

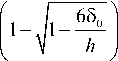
; X 4 =

h § 0

1 -

1 -

6 § 0

л \ t 11 du|

612 (xi ) = Lh\ З

V dxiJ

а также момента (21):

■ .  (   \      ^{1 h du} j     ^h    f¹

M 11 ^{( X}1 ) = D I V^--ТФ I •

V 2 dx_}    3 J

Удовлетворение решений (44)–(46) двенадцати условиям сопряжения (27)–(32) и трем граничным условиям (36)-(38) дает решение поставленной задачи, из которого, при Р _р = 0, приходим к следующему значению напряжения в слое:

^О 22 1 x 1 = 0

2 72 6 2 0з а ₊j_ | 7§ h V h 72 J •

„    §0 h , .

При —, — «£ 1; ^ — го из решения задачи приходим ha к асимптотическому выражению вертикального перемещения на границе упругой и пластической зон:

2 у = 2 у ° ,

u^ "I    =               Q 2    + a^ °"" p -°o^p+ Qi

² ^ = i p    EN h h      ^V p    ^}    2        ° p

к                                       7

где 2 у = —22- §₀ - энергетическое произведение [30]. 2 E ⁰

В условии (50) используется сингулярное представление напряжения й22 в виде (47). Из (49) выразим положительное значение длины пластической области:

из последнего выражения, с учетом (3), (6) и (7), – к связи:

p

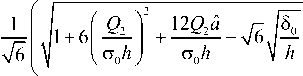
— 1 +

Преобразуем выражение

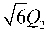
о ° ^h

. (51)

^ 22 Li =_tp =^ ° =

(51) с учетом (50) при

8₀ —> ° + ° :

-g°< p + Q 2 .  (48)

Q 2

Из выражения (48) находим представление внешней нагрузки с условием конечности напряжения 7 в виде

У² Y ° ^Eh У2 ( 1 + Уб a )

( 1 + 26 p § ) ,

_ о ° h \j § ° + ^2/ p + Уб/ p

²    1 + Уб ( Ip + a )

§     §о О, pP , a где §° =—; p= = ТУ a = 7. h        hh

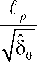
приведенная безразмерная длина пла-

Если §₀ — ° + ° , то из (49) приходим к выражению

стической зоны.

В отличие от предыдущих зависимостей внешней нагрузки от длины пластической зоны, выражение (52) учитывает стадию упругого деформирования и при переходе к математическому разрезу, когда ° <  Q <  Q_e .

Здесь Q e =

Q = ^ ° h

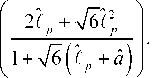
У 2Y ° ^Eh У2 ( 1 + У6 a )

– упругая составляющая внеш-

Из последнего выражения следует, что при переходе к математическому разрезу стадия упругого деформирования отсутствует и при сколь угодно малой величине внешней нагрузки возникает пластическая деформация. Такая же ситуация имеет место в модели Дагдейла [14] и в моделях с использованием когезионных сил сцепления [6–12].

Введение поправки Ирвина приводит к увеличению длины трещины за счет зоны пластичности на величину

K ²

£ =----. Поскольку коэффициент интенсивности

p   2по0

напряжений K пропорционален внешней нагрузке, то и в модели квазихрупкого разрушения пластическая область возникает в начале нагружения. Таким образом, в случае математического разреза классические условия пластичности приводят к невозможности описания стадии чисто упругого деформирования.

Локальное условие пластичности. Сформулируем условие пластичности, позволяющее отразить стадию упругого деформирования при вырождении физического разреза в математический. Предполагаем, что в диапазоне толщины слоя ° < § ° < § ° условие пластичности имеет вид

ней нагрузки. Определяя в эксперименте значение упругой составляющей, находим предел упругости энергетического произведения в виде

2 ( 1 + Уб a ) ² Q e

2y° =     Eh

В статье [32] приведены результаты экспериментов по определению трещиностойкости G адгезива AV138. Образец состоит из двух пластин толщиной B в направлении, ортогональном плоскости x0x  (см. ри сунок), соединенных тонким слоем адгезива на части пластин. Образец нагружается расклинивающими силами N = Q^B. Определяется зависимость силы N от перемещения точки ее приложения – u. Приведены линейные размеры образца, мм: h = 3; B = 25; a = 4° и значение модуля Юнга E = 4.9 -1°3 Н/мм2. Из приведенных зависимостей внешней силы от перемещения точки ее приложения можно оценить величину упругой составляющей N = QeB - 30 Н. Подставляя приведенные значения в формулу (53), получим значение 2у0 ~ °.22 Н/мм. В статье [32] приведено среднее значение трещи-ностойкости GIC = °.14 Н/мм, полученное в результате испытания шести образцов.

Выделим нагрузку, связанную с пластической деформацией Qp = 2Qelpб, тогда Q2 = Qe + Qp и с ростом пластической зоны растет параметр lp5. Используя экспериментальные зависимости внешней нагрузки от перемещения, исходя из выражения 5 = 0.5 Q2(u) -1 , pU      I Qe     )

можно установить закон изменения параметра l от u .

Заключение

В результате упрощенного аналитического решения задачи упругопластического деформирования ДКБ-образца получены следующие результаты:

• 1.    Установлена зависимость полей перемещений и напряжений от длины и толщины слоя взаимодействия. Напряжения обратно пропорциональны корню квадратному от толщины слоя и убывают по экспоненте вдоль длины слоя.

• 2.    Использование классического условия перехода в пластическое состояние отражает упругую стадию деформирования только при конечной толщине слоя взаимодействия. При переходе к математическому разрезу пластическая составляющая деформации, как и в моде-