Модель движения частиц зернового вороха при работе ленточного метателя

В связи с острой необходимостью создания современной техники для послеуборочной обработки зернового вороха, работающих на инновационных принципах назрела задача создать математическую модель движения частиц обрабатываемого материала при работе ленточного метателя с тем, чтобы его существенно модернизировать. Это позволит разработать машину нового поколения.

Рассмотрим свободное движение частиц зернового воздуха в неподвижной воздушной среде при работе ленточного метателя.

Введем следующие обозначения (рисунок 1.):

t - время, с;

О xy - неподвижная система декартовых координат с началом О на оси вращения верхнего вальца, горизонтальной осью О x и вертикальной осью О у , направленной вертикально вверх;

R - радиус верхнего вальца (шкива) ленточного метателя, м;

..?. - угол, образуемый отрицательной полуосью Оx, и прямой ОВ, соединяющей центры верхнего 1 и нижнего 2 вальцов в вертикальной плоскости рад;

ю - угловая скорость вращения верхнего вальца, рад/с;

5 - величина ускорения 5 свободного падения материальной точки, м/с2;

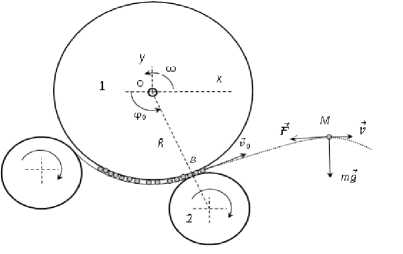
Рисунок 1. Схема действия сил на материальную точку при работе ленточного метателя

Представим частицу зернового вороха в виде материальной точки М.

Пусть (рисунок 1)

x , y , z - координаты движущейся материальной точки М ;

Г - величина вектора Г скорости точки М , м/с;

Г; - величина вектора i\ начальной скорости точки М, м/с m - масса материальной точки М, кг;

$ - величина ускорения ^f.- материальной точки М , м/с²;

г - величина силы F сопротивления воздуха, Н;

Y - удельный вес воздуха, Н/м3;

к - коэффициент сопротивления воздуха;

kp - коэффициент парусности частицы, 1/м.

Дифференциальное уравнение движения свободной материальной точки М в векторном виде записывается так [1]:

ma=mg + F ,                   (1)

где

S т 2          т

Г = — К „ ? ? П •- - = - К „ а И .

Коэффициент парусности ^; прямо пропорционален площади S миделева сечения ча стицы и определяется по формуле [2]

= Ь^/(??<::.

Проецируя обе части векторного равенства (1) на оси координат О х, О у , запишем дифференциальные уравнения движения точки М в координатном виде (рисунки 1.,2):

Г d?x , dx dt2        р dt

I d2y, dy

\^r = -g -k-u—(2)

dt2 y P dt d2z , dz

— = —k-v—, v dt2 p dt где г = Jx2 J*2 z2.

При ленточном метании все частицы сбрасываются в точке В касания лент между вальцами (шкивами) 1, 2 с одинаковой начальной скоростью i \

Данные конструктивно-кинематических параметров ленточного метателяи свойств зернового вороха представлены в таблице 1.

Таблица 1

R , м	0), рад/с	зерно, АР1, 1/м	примеси, кр2 , 1/м	фо, °	9 , м/с2
0,54-1,0	154-25	0,084- 0,1	1,04-2,0	1104- 13 5	9,81

Для решения системы нелинейных дифференциальных уравнений (2) необходимо задать начальные условия.

Начальными условиями служат координаты ,'^;<, 'Л, 2; точки В касания лент, натянутых на вальцы 1 и 2 и между которыми движется зерновой ворох, и скорость .^;V, 'Л, 7; точки М в момент выброса в точке В.

Система дифференциальных уравнений (2) не имеет аналитического решения и была решена численным методом Рунге-Кутта [3, с. 708].

Движение зернового вороха в ветровом потоке

Рассмотрим свободное движение материальной точки М массы m в вороха потоке. В частном случае такой поток может быть направлен навстречу оси О х или перпендикулярно плоскости О ху . Пусть (рисунок 2)

F - величина вектора i7 скорости ветрового потока (частицы воздуха), м/с;

Гг; , г.-, , iV- - проекции вектора IV на оси О х , О у и О z , перпендикулярную плоскости О ху , м/с;

•V - величина вектора V.. скорости частицы относительно ветрового потока, м/с.

Придерживаясь прежних обозначений, перепишем уравнение (1) применительно к случаю свободного движения частицы в ветровом потоке:

??;5 = ??г^ 7- F.                                   (3)

где г = —kpmv/ — = -kpmvrvT.

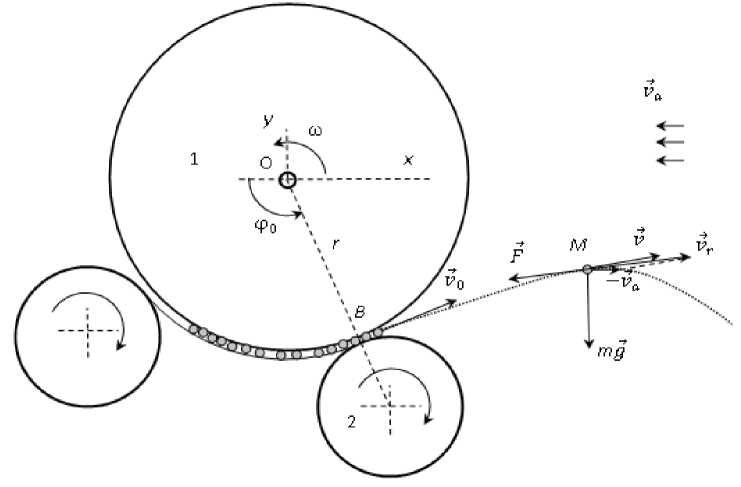
Рисунок 2. Схема действия сил на материальную точку в ветровом потоке

Так как

5 , то векторное уравнение (3) можно переписать в виде

г ria   гпд Крггць ^ cz IV ^aJ

Проецируя обе части векторного уравнения (4) на неподвижные координатные оси О х , О у и О z , придем к следующей системе нелинейных дифференциальных уравнений второго порядка:

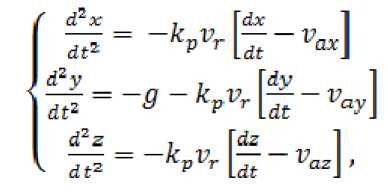
d?z dt2

где у + Cz-vazy.

Для решения системы дифференциальных уравнений (5) необходимо задать начальные условия и проекции ^£UC , г? , ^02 вектора Pq на оси О х , О у и О z .

В частности, при встречном воздушном потоке ^clx ^a , ^гау = 0 , ^Va^ — 0

Начальными условиями служат координаты Xq , Уо , ^o точки В касания лент, натянутых на вальцы 1 и 2 и между которыми движется зерновой ворох, и скорость ^Q , Уо , ^o точки М в момент выброса в точке В .

Система дифференциальных уравнений (4) не имеет аналитического решения и была решена численным методом Рунге-Кутта при встречном и боковом воздушных потоках.

Таким образом, полученные знания позволяют значительно расширить знания в этой области, что в свою очередь создает предпосылки для математических моделей, описывающих работу метателей зерна нового поколения, функционирующих на более высоком качественном уровне.