Model-Free Adaptive Fuzzy Sliding Mode Controller Optimized by Particle Swarm for Robot Manipulator

Published Online May 2013 in MECS

Sliding Mode Controller has been widely applied to various types of non-linear systems. SMC’s popularity is due to its robustness against the changes in parameters and the external disturbances [1] in both theoretical and practical applications. However, the action of discontinuous part in traditional SMC leads the whole controller to face a troublesome condition known as "chattering" [2], and the traditional type of SMC requires the whole dynamic functions of the system. Moreover, in order to achieve the non-chattering SMC, the sign function should be changed to saturation function to employ the adaptation of a thin boundary layer close by the sliding manifold to minimize or attenuate the chattering [3]. However, this method damages the perfect tracking of the SMC; hence, the steady state error will always exist. Furthermore, to overcome the mentioned problem, some adaptive strategies recommended compensating the disturbances in order to increase the tracking performance [38-44].

In recent decades, the Fuzzy Logic, as a technique based on expert knowledge has been applied to a wide range of controllers for solving the complex problems. Although Fuzzy controller is free from huge mathematical operations, sometimes more mathematical treatment is needed. However it should be noted that sometimes using Fuzzy Logic Controller is much more tranquiller [4-7, 24]. Today’s, applying the techniques that combine the fuzzy theory with the nonlinear controllers, for instance using fuzzy sliding mode controller, are most common. The applications of fuzzy logic controller can not only be used in the systems with hard modeling, but they can also be used for systems with high mathematical analysis.

The robust model of fuzzy combination, so called adaptive fuzzy sliding mode, was introduced to reject the chattering phenomenon and compensate unknown dynamics parameters in the systems by another fuzzy logic controller [8].Some researchers recommended some improvements applied to this method [9-14].The adaptive controller defines in two groups: traditional and indirect groups where the first one requires some main parameters of the system and the other, such as fuzzy adaptive method, adjusts the parameter variations by the expert’s knowledge [15-24].

The controller under consideration is based on the Yoo and Ham approach with some major changes. The saturation function is used instead of sign function to plenty avoid the chattering. Furthermore, the adaptive fuzzy inference system is utilized to avoid the disturbances and eliminate the chattering. The substitution of another Fuzzy Logic Controller with 49 rules by the equivalent part compensates the unknown part of model. Subsequently, the Coefficients were optimized by Particle Swarm Optimization.

This algorithm determines better values for sliding surface slope. The Off-line PSO method is applied in Copyright © 2013 MECS systems whose dynamic parameters are variable. Integrated PSO method to AFSMC, FSMC, and SMC controllers will cause better performance by off-line tuning the nonlinear and time variant coefficients [43-47]. In a nutshell the proposed controller is successfully applied to PUMA 560.

The simulation results show comparison between the proposed model free adaptive fuzzy sliding mode controller optimized by PSO (AFSMC-PSO), model free fuzzy sliding mode controller optimized by PSO (FSMC-PSO), classical sliding mode controller optimized by PSO (SMC-PSO) for different performance indices like the RMS error, steady state error, trajectory tracking, disturbance rejection, and chattering performance.

This paper is organized as follows: A short description of classical sliding mode controller (SMC) and problem statement, the modeling of robot manipulator, a brief description of fuzzy logic system are included in section 2. In Section 3 the summary of FIS is presented, a brief explanation about model-free fuzzy sliding mode controller (FSMC), the proposed adaptive fuzzy sliding mode control and a brief description of Particle Swarm Optimization is presented in section 3. The Simulation results for the proposed controller are included in Section 4. Finally, the paper is concluded in Section 5.

• II.    THEORY

Sliding Mode Controller: The explanation and problem statement of classical sliding mode controller and its solutions was introduced by some researchers [9, 25-29]. According to the above references, the multi degrees of freedom robot manipulator control law can be presented as:

τ =τ eq + τ dis (1)

Where, τeq is a model-based parameter used to compensate the nominal dynamics of system. The τeq and τdis are both calculated respectively as:

Teq = [M-1(B + C + G) + S] M (2)

	"b 112q1q2+ b113q1 q 3+ 0 + b123q2q3 0 + b 223 q 2 q 3 + 0 + 0
S + C + G =	, ■ ■ , 0 . . b 412 q 1 q 2 + b 413 q 1 q 3 + 0+0

		C 12 q 22 + C 13 q 32 C 21 q 1 2 + C 23 q 3 2 C 31 q 12 +C 32 q 22		+	A ■ .g,	, S -	[S 2 I S 3 S 4 A 6	,
		C 51 q 12	0 +C 52 q 2 0
	M 11	M 12	M 13	0	0		0
	M 21	M 22	M 23	0	0		0
M=	M 31	M 32	M 33	0	M 35		0
	0	0	0   M 44		0		0
	0	0	0	0	M 55		0
	L 0	0	0	0	0   M 66
τ dis = K. sgn(S)								(3)
Where
S = e + X * e + (Z/2)			2 [ edt					(4)

Generally, the sign function replaces by saturation function to decrease the chattering phenomenon.

T dis = К. sgn^(S/₀)                               (5)

т = T eq + K. sgn (^S/0) =                        ⁽⁶⁾

T eq + k.sgn(^s/0) ,|S| > 0

T eq + k.sgn(^s/0) ,|S| < 0

Modeling the Formulation of Robot Manipulator: The robot dynamic formulation with rigid links can be displayed as [28, 32-33]:

M(q)q + V(q, q) +G(q) = Г                 (7)

Where:

M(q) is the mass matrix or kinetic energy matrix and G(q) is the gravity forces.

V(q, q)is the centrifugal and coriolis forces.

The total parameters of matrices are depending on the position of robot. Any changes in nonlinear parameters such as Coriolis and Centrifugal functions can cause changes in velocities and subsequently in position. In this case, the robot dynamic equation known as configuration space or C-space, which is the space of all possible configurations, can be demonstrated as:

V(q,q) = B(q). ^[q. q] + c(q)^[q 2 ] ^ т =         (8)

M⁽q).q + B⁽Q^)[q. q] + C⁽q^)[q 2 ] + G(q)

Where, B ( q ) is a [n x n(n — 1)/2 ]matrix of Coriolis torque. C ( q ) is a [n x n] matrix of Centrifugal torques. [ qq ] is a [n(n — 1)/2 x 1] vector of joint velocity products given by:

^T [ q ₁ . q ₂ , q ₁ . q ₃ ,..., q ₁ . q_n , q ₂ . q ₃ , q ₂ . q ₄ ,..., q_{n - 2} . q_n , q_{n - 1} . q_n ] [ q ² ]is a [ nx1] vector given by: [ q 1² , q ₂2 ,...., q n 2 ]

Some researches perform either the summation of Lagrange’s formulation or the Gibbs-Alembert formulation to obtain the kinetic energy matrix and gravity vector which can be used to derive the dynamic modeling of the robot manipulators. The following equation shows the angular acceleration:

q = M - ¹ (q). {t — [S(q). qq + C(q). q² +       (9)

gq}

In this paper first 3 degrees of freedom PUMA 560 robot manipulator is modeled and discussed.

The Fuzzy Logic Controller: Fuzzy Logic theory (FL) introduced by Zadeh in 1965 and utilized in large range of areas. Fuzzy Logic System utilizes estimation capabilities to capture uncertainties under simple mathematically model and also it is a free-model controller. There are two most applicable methods that can be used in fuzzy logic controller, namely, Sugeno method and Mamdani method. In this study the latter is used. In aggregation part the max-min method is applied as below:

iL⁽Х к ,У к ,и) = f_u r FR i ⁽Х к ,У к ,и) =             ⁽¹⁰⁾

u                   u i=1

maxi'{min r=i [q _R₽^ ⁽X k ,y k ), q p_m ⁽U)]}

To accomplish the defuzzification phase the "Center Of Gravity" method (COG) has chosen in this paper. Equation below illustrates the formula of it:

COG(xkyk) =

ZiUi zr=i. ^u(Xk,ykUk) Ei Zr=i . Hu (xk,yk,Ui)

output are indicated in Figure.2. The fuzzy control rules which are based on Mamdani method mare shown in

• III.    METHODOLOGY

Design Fuzzy Sliding Mode Controller: In this section, the combination of fuzzy logic with sliding mode is discussed to make a new controller so called model free fuzzy sliding mode controller (FSMC). This approach achieved by replacing the FLC with the equivalent dynamic part in SMC formulation stated in equation Teq = [M-1(B + C + G) + S] M . Considering the note that, SMC is known for its robustness and stability, in which the FSMC inherits these features. Moreover some problems such as sensitivity to changes in system parameters and dependency to dynamic parameters are solved. Figure.1 displays this design procedure.

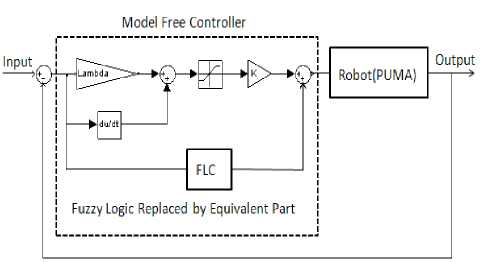
Figure1: Block Diagram of Model-Free Fuzzy Sliding Mode Controller for Robot Manipulator

Fuzzy logic controller which is replaced by equivalent dynamic part (Teq )in SMC formulation [24] includes two inputs (error (e) and error change (e) ) and an output (Teq) that simulate the equivalent dynamic part of the SMC. Linguistic variables of inputs and output have been classified as: N.B= Negative Big, N.M= Negative Medium, N.S= Negative Small, Z=Zero, P.S=Positive small, P.M= Positive Medium, P.B= Positive Big. The triangular membership functions for both inputs and the

Table.1and the COG (Center Of Gravity) method is used in defuzzification step.

Table1: Fuzzy rule base

e e	NB	NM	NS	ZE	PS	PM	PB
NB	PB	NB	NB	NM	NS	NS	ZE
NM	NB	NM	NM	NM	NS	ZE	PS
NS	NB	NM	NS	NS	ZE	PS	PM
ZE	NB	NM	NS	ZE	PS	PM	PB
PS	NM	NS	ZE	PS	PS	PM	PB
PM	NS	ZE	PS	PM	PM	PM	PB
PB	PS	PS	PM	PB	PB	NB	ZE

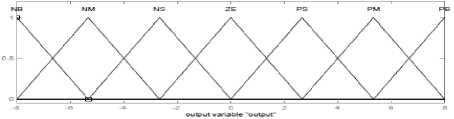
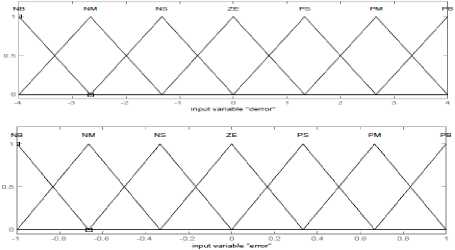
Figure2: Triangular membership function for e, e and T _eq .

Adaptive Fuzzy Sliding Mode Controller: SMC’s restrictions which occur under various operating conditions can be solved by the proposed controller. In order to overcome these flaws the combination of the SMC and the fuzzy system is recommended to estimate the indefinite plant functions in the SMC’s design. This controller is efficient in the system which its dynamics part is unknown [35]. Furthermore, the adaptation law plus FSMC can provide a system with online tuning and learning. This controller enhances the system tracking performance and eliminates the steady-state error. The adaptive fuzzy system maintains suitable performance for systems in which enormous uncertainties occur in them and unknown changes affect in the plant’s parameters.

The two main benefits of this supervisory tuning method are to guarantee the behavior of the model-free plant and enhance system performance.

Adaptation in fuzzy controller is classified into two categories: direct adaptive and indirect adaptive methods, where a direct adaptive nonlinear method tunes the controller inputs parameters, and an indirect supervisory method tunes the parameters of control system based on operating conditions [36]. There are different adaptations algorithms applied to the plants, which are discussed in the following references [37].

Although the SMC has great robustness, it is difficult for this controller to handle unstructured model uncertainties.

Adaptation is utilized to deal with uncertainties and external variations. In this work, the controller under consideration is free from dynamics model; therefore the indirect method is used to adapt the two gain updating factors (G1, G2) which are both nonlinear and time variant parameters. The schematic block diagram of the proposed mode free adaptive fuzzy sliding mode controller is depicted in Figure.3.

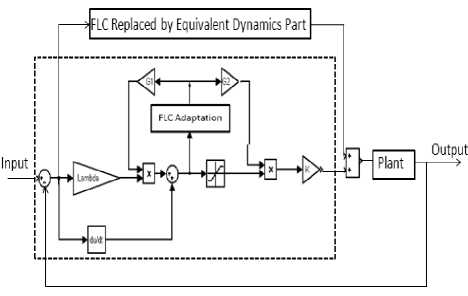
Figure3: Block Diagram of Adaptive Fuzzy Sliding Mode

Controller for Robot Manipulator

The FLC which adapts the plant to various perturbations and disturbances has one input (s) and one output (α). This FL supervisor improves the tracking trajectory by online tuning the controller parameters and the output (α) tunes the coefficients (G1, G2). Triangular membership functions, linguistic variables, and the quantization of values for both input and output is shown is Figure.4.The rule base table for the fuzzy logic supervisory is brought in Table.2.

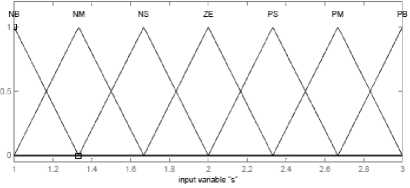
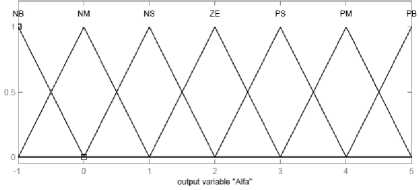
Figure4: Triangular membership function for (s) and (α).

The FLC which makes the main controller free from model has two inputs (e, e ) and one output (Teq). The linguistic variables for error (e) are; N.B, N.M, N.S, ZE, P.S, P.M, P.B, and the linguistic variables for change of error (e ) are :Fast Left(FL), Medium Left(ML), Slow Left(SL),Zero(Z), Slow Right (SR), Medium Right(MR), Fast Right(FR), and the linguistic variables to find the output are; Large Left(L.L), Medium Left(M.L), Small Left(S.L), Zero(Z), Small Right(S.R), Medium Right(M.R), Large Right(L.R) . The triangular membership functions of inputs and output with their quantization of values are displayed in Figure.4 and the rule base table is brought in Table.3.

Table.2: FL Supervisory Rule Base

S	NB	NM	NS	ZE	PS	PM	PB
α	NB	NM	NS	ZE	PS	PM	PB

Table.3: Fuzzy rule base

e ё\	FL	ML	SL	ZE	SR	MR	FR
NB	LL	LL	LL	ML	SL	SL	ZE
NM	LL	ML	ML	ML	SL	ZE	SR
NS	LL	ML	SL	SL	ZE	SR	MR
ZE	LL	ML	SL	ZE	SR	MR	LR
PS	ML	SL	ZE	SR	SR	MR	LR
PM	SL	ZE	SR	MR	MR	MR	LR
PB	ZE	SR	SR	MR	LR	LR	LR

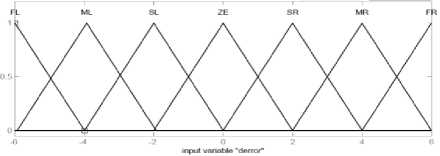
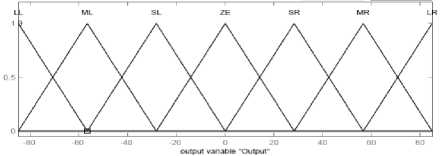
Figure5: Triangular membership function for e, e and T eq .

Particle Swarm Optimization Algorithm: The evolutionary PSO algorithm extracted from the social movement feature of the birds in the flock in search of food. First introduced by Eberhart and Kennedy in 1995 [46]. The enchanting features of implementing this easy algorithm are its robustness in tuning the coefficient of sliding surface and its global and local search structure. The symbolic attributions of this algorithm accompany with the mathematical implementation structure was introduced in [43, 44] papers.

As mentioned in formulations (3) and (4), Luanda (λ) and (K) are coefficients having significant impact on discontinuous component; the external noise will cause changes on error rate and chattering in torque values with low amplitudes by altering these parameters. So, if these coefficients tune appropriately the sliding mode controller can reject perturbations more desirably. The integration of PSO algorithm with the other classical controller will deplete the chattering phenomenon by offline tuning. The PSO algorithm was applied on all the three presented algorithms in this paper. Namely, SMC, FSMC, and AFSMC and has a significant excellence in comparison the ordinary one which also demonstrated in Piltan, F., et al. papers [43-44]. In this paper, PSO is used to improve the results by revolutionary algorithms instead of traditional try and error method.

• IV.    SIMULATION RESULTS:

• 45.02

• 24.98

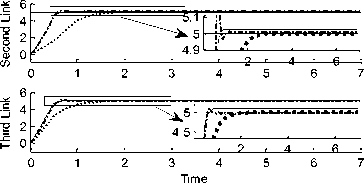
Model-free adaptive fuzzy sliding mode controller (AFSMC), Model-free fuzzy sliding mode controller (FSMC) and Sliding Mode Controller (SMC) were examined for step response trajectories. In this simulation the first, second, and third joints move from initial point to target position considering with and without external disturbances. The simulations were accomplished in Matlab/Simulink. The comparisons were conducted on indices namely, tracking trajectory, error rate in performance, chattering rejection and robustness (Disturbance rejection).

Tracking Performances: As it is apparent in Figure.6 AFSMC and FSMC have the best tracking performance and settling time but SMC has the best steady state error in every three links while these is no external disturbances. In second phase of examination an unknown output disturbance is applied to system and the results in Figure.7 demonstrate that the proposed AFSMC has the best disturbance rejection and stable tracking trajectory than the others which eliminates any kind of perturbations applied to system. The noise amplitude is equal to 50% of input amplitude and it was exerted simultaneously at the beginning of the process.

---Desired(Step)

................ SMC Response

-----------FSMQ Response

-------AFSMC Response

Legend

Figure6: Step Response of SMC, FSMC, AFSMC for first, second and third link trajectory without external disturbance

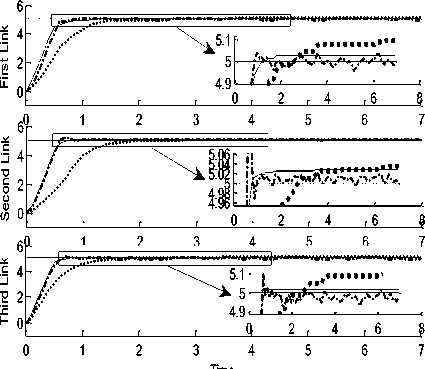
Figure7: Step Response of SMC, FSMC, AFSMC for first, second and third link trajectory with external disturbance

Time

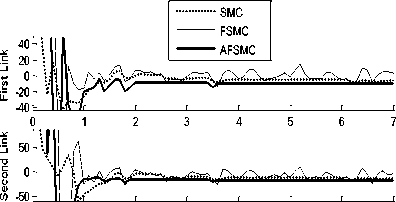
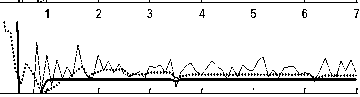
Figure8: Torque trend and chattering rejection test to investigate the robustness for all links

Error rate: Although SMC gives the least error changes compared to others (refer to Table.4), it has high oscillation tracking which causes instability and chattering phenomenon at the presence of disturbances because when there is no noise the error rate in SMC is zero. As it is obvious in Table.4 proposed AFSMC has error reduction in noisy environment compared to condition without any disturbance and displays smoother trend in above profiles.

Table4: RMS Error Rate of Presented controllers

RMS Error Rate	SMC	FSMC	AFSMC
Without Noise	0	0.01	0.04
With Noise	0.062	0.014	0.01

Chattering rejection and robustness: As it was mentioned, a white noise as an external disturbance was applied to system to investigate the disturbance rejection of the system. The results are illustrated in Figure.8. At the presence of noise the SMC and FSMC have high oscillations (chattering). The proposed AFSMC has the best performance because it has no chattering phenomenon in its torque and has a stable procedure.

• V.    CONCLUSION

This paper provides a novel methodology in designing model free adaptive fuzzy sliding mode controller applied to PUMA 560 industrial robot manipulator. Simulation results demonstrate that proposed model-free AFSMC has a better performance than SMC and FSMC, because this controller can adapt itself to system parameter’s changes and external disturbances. In AFSMC, the fuzzy supervisory can change the λ to achieve the best performance but the FLC in FSMC just make the controller free from model. The proposed AFSMC has robustness, stability and resistance against the external disturbances. Moreover the fuzzy supervisory makes it smooth and without any high oscillation (chattering) in tracking trajectory and torque. At last PSO algorithm is applied to adjust the sliding function parameters to minimize the chattering movements by off-line tuning.